吴恩达深度学习笔记:深度学习的 实践层面 (Practical aspects of Deep Learning)1.13-1.14
目录
- 第二门课: 改善深层神经网络:超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)
- 第一周:深度学习的 实践层面 (Practical aspects of Deep Learning)
- 1.13 梯度检验(Gradient checking)
- 1.14 梯 度 检 验 应 用 的 注 意 事 项 ( Gradient Checking Implementation Notes)
第二门课: 改善深层神经网络:超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)
第一周:深度学习的 实践层面 (Practical aspects of Deep Learning)
1.13 梯度检验(Gradient checking)
梯度检验帮我们节省了很多时间,也多次帮我发现 backprop 实施过程中的 bug,接下来,我们看看如何利用它来调试或检验 backprop 的实施是否正确。
假设你的网络中含有下列参数, W [ 1 ] W^{[1]} W[1]和 b [ 1 ] b^{[1]} b[1]…… W [ l ] W^{[l]} W[l]和 b [ l ] b^{[l]} b[l],为了执行梯度检验,首先要做的就是,把所有参数转换成一个巨大的向量数据,你要做的就是把矩阵𝑊转换成一个向量,把所有𝑊矩阵转换成向量之后,做连接运算,得到一个巨型向量𝜃,该向量表示为参数𝜃,代价函数𝐽是所有𝑊和𝑏的函数,现在你得到了一个𝜃的代价函数𝐽(即𝐽(𝜃))。接着,你得到与𝑊和𝑏顺序相同的数据,你同样可以把 d W [ 1 ] dW^{[1]} dW[1]和 d b [ 1 ] db^{[1]} db[1]…… d W [ l ] dW^{[l]} dW[l]和 d b [ l ] db^{[l]} db[l]转换成一个新的向量,用它们来初始化大向量𝑑𝜃,它与𝜃具有相同维度。
同样的,把 d W [ 1 ] dW^{[1]} dW[1]转换成矩阵, d b [ 1 ] db^{[1]} db[1]已经是一个向量了,直到把 d W [ l ] dW^{[l]} dW[l]转换成矩阵,这样所有的𝑑𝑊都已经是矩阵,注意 d W [ 1 ] dW^{[1]} dW[1]与 W [ 1 ] W^{[1]} W[1]具有相同维度, d b [ 1 ] db^{[1]} db[1]与 b [ 1 ] b^{[1]} b[1]具有相同维度。经过相同的转换和连接运算操作之后,你可以把所有导数转换成一个大向量𝑑𝜃,它与𝜃具有相同维度,现在的问题是𝑑𝜃和代价函数𝐽的梯度或坡度有什么关系?

这就是实施梯度检验的过程,英语里通常简称为“grad check”,首先,我们要清楚𝐽是超参数𝜃的一个函数,你也可以将𝐽函数展开为𝐽(𝜃1, 𝜃2, 𝜃3, … … ),不论超级参数向量𝜃的维度是多少,为了实施梯度检验,你要做的就是循环执行,从而对每个𝑖也就是对每个𝜃组成元素计算𝑑𝜃approx[𝑖]的值,我使用双边误差,也就是
d θ a p p r o x [ i ] = J ( θ 1 , θ 2 , . . . . . . θ i + ε , . . . ) − J ( θ 1 , θ 2 , . . . . . . θ i − ε , . . . ) 2 ε dθ_{approx}[i] =\frac{J(θ_1,θ_2,......θ_i+ε,...) - J(θ_1,θ_2,......θ_i-ε,...)}{2ε} dθapprox[i]=2εJ(θ1,θ2,......θi+ε,...)−J(θ1,θ2,......θi−ε,...)
只对 θ i θ_i θi增加𝜀,其它项保持不变,因为我们使用的是双边误差,对另一边做同样的操作,只不过是减去𝜀,𝜃其它项全都保持不变。

从上节课中我们了解到这个值( d θ a p p r o x [ i ] dθ_{approx}[i] dθapprox[i])应该逼近𝑑𝜃[𝑖]=𝜕𝐽/𝜕𝜃𝑖,𝑑𝜃[𝑖]是代价函数的偏导数,然后你需要对𝑖的每个值都执行这个运算,最后得到两个向量,得到𝑑𝜃的逼近值 d θ a p p r o x dθ_{approx} dθapprox,它与𝑑𝜃具有相同维度,它们两个与𝜃具有相同维度,你要做的就是验证这些向量是否彼此接近。
具体来说,如何定义两个向量是否真的接近彼此?我一般做下列运算,计算这两个向量的距离,𝑑𝜃approx[𝑖] − 𝑑𝜃[𝑖]的欧几里得范数,注意这里(||𝑑𝜃approx − 𝑑𝜃||2)没有平方,它是误差平方之和,然后求平方根,得到欧式距离,然后用向量长度归一化,使用向量长度的欧几里得范数。分母只是用于预防这些向量太小或太大,分母使得这个方程式变成比率,我们实际执行这个方程式,𝜀可能为 1 0 − 7 10^{−7} 10−7,使用这个取值范围内的𝜀,如果你发现计算方程式得到的值为 1 0 − 7 10^{−7} 10−7或更小,这就很好,这就意味着导数逼近很有可能是正确的,它的值非常小。
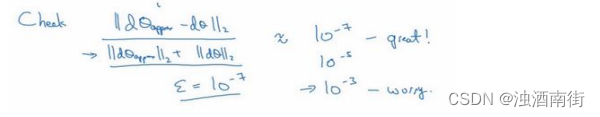
如果它的值在 1 0 − 5 10^{−5} 10−5范围内,我就要小心了,也许这个值没问题,但我会再次检查这个向量的所有项,确保没有一项误差过大,可能这里有 bug。
如果左边这个方程式结果是 1 0 − 3 10^{−3} 10−3,我就会担心是否存在 bug,计算结果应该比 1 0 − 3 10^{−3} 10−3小很多,如果比 1 0 − 3 10^{−3} 10−3大很多,我就会很担心,担心是否存在 bug。这时应该仔细检查所有𝜃项,看是否有一个具体的𝑖值,使得𝑑𝜃approx[𝑖]与𝑑𝜃[𝑖]大不相同,并用它来追踪一些求导计算是否正确,经过一些调试,最终结果会是这种非常小的值( 1 0 − 7 10^{−7} 10−7),那么,你的实施可能是正确的。

在实施神经网络时,我经常需要执行 foreprop 和 backprop,然后我可能发现这个梯度检验有一个相对较大的值,我会怀疑存在 bug,然后开始调试,调试,调试,调试一段时间后,我得到一个很小的梯度检验值,现在我可以很自信的说,神经网络实施是正确的。
现在你已经了解了梯度检验的工作原理,它帮助我在神经网络实施中发现了很多 bug,希望它对你也有所帮助。
1.14 梯 度 检 验 应 用 的 注 意 事 项 ( Gradient Checking Implementation Notes)
这节课,分享一些关于如何在神经网络实施梯度检验的实用技巧和注意事项。

首先,不要在训练中使用梯度检验,它只用于调试。我的意思是,计算所有𝑖值的 d θ a p p r o x [ i ] dθ_{approx}[i] dθapprox[i]是一个非常漫长的计算过程,为了实施梯度下降,你必须使用𝑊和𝑏 backprop 来计算𝑑𝜃,并使用 backprop 来计算导数,只要调试的时候,你才会计算它,来确认数值是否接近𝑑𝜃。完成后,你会关闭梯度检验,梯度检验的每一个迭代过程都不执行它,因为它太慢了。
第二点,如果算法的梯度检验失败,要检查所有项,检查每一项,并试着找出 bug,也就是说,如果 d θ a p p r o x [ i ] dθ_{approx}[i] dθapprox[i]与𝑑𝜃[𝑖]的值相差很大,我们要做的就是查找不同的𝑖值,看看是哪个导致 d θ a p p r o x [ i ] dθ_{approx}[i] dθapprox[i]与𝑑𝜃[𝑖]的值相差这么多。举个例子,如果你发现,相对某些层或某层的𝜃或𝑑𝜃的值相差很大,但是dw[𝑙]的各项非常接近,注意𝜃的各项与𝑏和𝑤的各项都是一一对应的,这时,你可能会发现,在计算参数𝑏的导数𝑑𝑏的过程中存在 bug。反过来也是一样,如果你发现它们的值相差很大, d θ a p p r o x [ i ] dθ_{approx}[i] dθapprox[i]的值与𝑑𝜃[𝑖]的值相差很大,你会发现所有这些项目都来自于𝑑𝑤或某层的𝑑𝑤,可能帮你定位 bug 的位置,虽然未必能够帮你准确定位 bug 的位置,但它可以帮助你估测需要在哪些地方追踪 bug。
第三点,在实施梯度检验时,如果使用正则化,请注意正则项。如果代价函数 J ( θ ) = 1 m ∑ L ( y ^ ( i ) , y ( i ) ) + λ 2 m ∑ ∣ ∣ W [ l ] ∣ ∣ 2 J(θ) =\frac{1}{m}\sum{L(\hat{y}^{(i)},y^{(i)})} + \frac{λ}{2m}\sum||W^{[l]}||^2 J(θ)=m1∑L(y^(i),y(i))+2mλ∑∣∣W[l]∣∣2,这就是代价函数𝐽的定义,𝑑𝜃等于与𝜃相关的𝐽函数的梯度,包括这个正则项,记住一定要包括这个正则项。
第四点,梯度检验不能与 dropout 同时使用,因为每次迭代过程中,dropout 会随机消除隐藏层单元的不同子集,难以计算 dropout 在梯度下降上的代价函数𝐽。因此 dropout 可作为优化代价函数𝐽的一种方法,但是代价函数𝐽被定义为对所有指数极大的节点子集求和。而在任何迭代过程中,这些节点都有可能被消除,所以很难计算代价函数𝐽。你只是对成本函数做抽样,用dropout,每次随机消除不同的子集,所以很难用梯度检验来双重检验dropout的计算,所以我一般不同时使用梯度检验和 dropout。如果你想这样做,可以把 dropout 中的 keepprob 设置为 1.0,然后打开 dropout,并寄希望于 dropout 的实施是正确的,你还可以做点别的,比如修改节点丢失模式确定梯度检验是正确的。实际上,我一般不这么做,我建议关闭 dropout,用梯度检验进行双重检查,在没有 dropout 的情况下,你的算法至少是正确的,然后打开dropout。
最后一点,也是比较微妙的一点,现实中几乎不会出现这种情况。当𝑤和𝑏接近 0 时,梯度下降的实施是正确的,在随机初始化过中……,但是在运行梯度下降时,𝑤和𝑏变得更大。可能只有在𝑤和𝑏接近 0 时,backprop 的实施才是正确的。但是当𝑊和𝑏变大时,它会变得越来越不准确。你需要做一件事,我不经常这么做,就是在随机初始化过程中,运行梯度检验,然后再训练网络,𝑤和𝑏会有一段时间远离 0,如果随机初始化值比较小,反复训练网络之后,再重新运行梯度检验。
这就是梯度检验,恭喜大家,这是本周最后一课了。回顾这一周,我们讲了如何配置训练集,验证集和测试集,如何分析偏差和方差,如何处理高偏差或高方差以及高偏差和高方差并存的问题,如何在神经网络中应用不同形式的正则化,如𝐿2正则化和 dropout,还有加快神经网络训练速度的技巧,最后是梯度检验。这一周我们学习了很多内容,你可以在本周编程作业中多多练习这些概念。祝你好运,期待下周再见。
相关文章:

吴恩达深度学习笔记:深度学习的 实践层面 (Practical aspects of Deep Learning)1.13-1.14
目录 第二门课: 改善深层神经网络:超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)第一周:深度学习的 实践层面 (Practical aspects of Deep Learning)1.13 梯度检验&#…...
笔试强训未触及题目(个人向)
1.DP22 最长回文子序列 1.题目 2.解析 这是一个区间dp问题,我们让dp[i][j]表示在区间[i,j]内的最长子序列长度,如图: 3.代码 public class LongestArr {//DP22 最长回文子序列public static void main(String[] args) {Scanner…...
)
【YOLO改进】换遍MMDET主干网络之EfficientNet(基于MMYOLO)
EfficientNet EfficientNet是Google在2019年提出的一种新型卷积神经网络架构,其设计初衷是在保证模型性能的同时,尽可能地降低模型的复杂性和计算需求。EfficientNet的核心思想是通过均衡地调整网络的深度(层数)、宽度࿰…...

uniapp下拉选择组件
uniapp下拉选择组件 背景实现思路代码实现配置项使用尾巴 背景 最近遇到一个这样的需求,在输入框中输入关键字,通过接口查询到结果之后,以下拉框列表形式展现供用户选择。查询了下uni-app官网和项目中使用的uv-ui库,没找到符合条…...

高斯数据库创建函数的语法
CREATE FUNCTION 语法格式 •兼容PostgreSQL风格的创建自定义函数语法。 CREATE [ OR REPLACE ] FUNCTION function_name ( [ { argname [ argmode ] argtype [ { DEFAULT | : | } expression ]} [, …] ] ) [ RETURNS rettype [ DETERMINISTIC ] | RETURNS TABLE ( { column_…...

【.NET Core】你认识Attribute之CallerMemberName、CallerFilePath、CallerLineNumber三兄弟
你认识Attribute之CallerMemberName、CallerFilePath、CallerLineNumber三兄弟 文章目录 你认识Attribute之CallerMemberName、CallerFilePath、CallerLineNumber三兄弟一、概述二、CallerMemberNameAttribute类三、CallerFilePathAttribute 类四、CallerLineNumberAttribute 类…...

ubuntu删除opencv
要完全删除OpenCV 3.4.5版本,你可以按照以下步骤进行操作: 卸载OpenCV库: 首先,你需要卸载OpenCV 3.4.5版本。可以使用以下命令卸载OpenCV库: sudo apt-get purge libopencv*这将删除OpenCV库及其相关文件。 删除O…...
K8s源码分析(二)-K8s调度队列介绍
本文首发在个人博客上,欢迎来踩! 本次分析参考的K8s版本是 文章目录 调度队列简介调度队列源代码分析队列初始化QueuedPodInfo元素介绍ActiveQ源代码介绍UnschedulableQ源代码介绍**BackoffQ**源代码介绍队列弹出待调度的Pod队列增加新的待调度的Podpod调…...
)
OpenGL ES 面试高频知识点(二)
说说纹理常用的采样方式? 最邻近点采样(GL_NEAREST)和双线性采样(GL_LINEAR)。 GL_NEAREST 采样是 OpenGL 默认的纹理采样方式,OpenGL 会选择中心点最接近纹理坐标的那个像素,纹理放大的时候会有锯齿感或者颗粒感。 **GL_LINEAR 采样会基于纹理坐标附近的纹理像素,计…...

2024第十六届“中国电机工程学会杯”数学建模A题B题思路分析
文章目录 1 赛题思路2 比赛日期和时间3 竞赛信息4 建模常见问题类型4.1 分类问题4.2 优化问题4.3 预测问题4.4 评价问题 5 建模资料 1 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 2 比赛日期和时间 报名截止时间:2024…...

面向对象的三大特性:封装、继承、多态
一、封装 封装是面向对象的核心思想。是以类为载体,将对象的属性和行为封装起来,对外隐藏其实现细节。 封装保证了类内部数据结构的完整性,使得外部(使用该类的用户)不能轻易地直接操作此数据结构,只能执…...
)
目标检测YOLO实战应用案例100讲-基于深度学习的交通场景多尺度目标检测算法研究与应用(中)
目录 3.4 实验结果与分析 深度融合注意力跨尺度复合空洞残差交通目标检测算法...

前端GET请求下载后端返回数据流文件,并且处理window.open方法跳转白屏方法
平时常用导出都是用window.open方法 点击跳转连接:使用 window.open 下载 const downError 地址?&参数${参数|| }; const downError Url/xxx/xxx?&orgId${orgId || };window.open(downError, "_self");//调用window.open方法导出 而使用…...

SD321放大器3V输入电流电压保护二极管25C电源电流
Sd 321运算放大器可以在单电源或双电源电压下工作, 可以使用最坏情况下的非反相单位增益连接来适应。如 具有真微分输入,并且保持在线性模式,输入共模电压 果放大器必须驱动较大的负载电容,则应使用较大的闭 为0。Vpc-这种放大器可…...

geoserver SQL注入、Think PHP5 SQL注入、spring命令注入
文章目录 一、geoserver SQL注入CVE-2023-25157二、Think PHP5 SQL注入三、Spring Cloud Function SpEL表达式命令注入(CVE-2022-22963) 一、geoserver SQL注入CVE-2023-25157 介绍:GeoServer是一个开源的地理信息系统(GIS&#…...

scrapy的入门
今天我们先学习一下scrapy的入门,Scrapy是一个快速的高层次的网页爬取和网页抓取框架,用于爬取网站并从页面中提取结构化的数据。 1. scrapy的概念和流程 1.1 scrapy的概念 我们先来了解一下scrapy的概念,什么是scrapy: Scrapy是一个Python编写的开源网络爬虫框架…...
大数据Scala教程从入门到精通第七篇:Scala在IDEA中编写Hello World
一:Scala在IDEA中编写Hello World 想让我们的idea支持scala的编写,需要安装一个插件。...

设计模式之数据访问对象模式
在Java编程的浩瀚星海中,有一个模式低调却强大,它像是一位默默无闻的超级英雄,支撑起无数应用的数据脊梁——那就是数据访问对象(DAO, Data Access Object)模式!想象一下,如果你能像操纵魔法一样…...

Spring aop切面编程
Spring aop切面编程 如何使用利用AuditAction创建切入点 如何使用 Aspect // 1. 创建一个类,用Aspect注解标记它,表明这是一个切面类。 Component public class LoggingAspect {// 2. 定义切点:在通知方法上,使用切点表达式来指定…...
如何更好地使用Kafka? - 事先预防篇
要确保Kafka在使用过程中的稳定性,需要从kafka在业务中的使用周期进行依次保障。主要可以分为:事先预防(通过规范的使用、开发,预防问题产生)、运行时监控(保障集群稳定,出问题能及时发现&#…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
