C++面向对象学习笔记五
本文主要讲解运算符重载,由于白鳯大佬没有具体讲解,所以本文自行补充了运算符重载的相关知识
目录
文章目录
前言
运算符重载
加号运算符重载
左移运算符重载
递增运算符重载
总结
前言
本文主要对于运算符重载进行探讨,分别对于成员函数重载和全局函数重载(友元函数重载)进行讨论。
运算符重载
运算符重载是C++中的一项强大功能,它允许您为自定义的类或结构体定义特定的行为,以响应与内置类型相似的操作符。通过重载运算符,您可以实现自定义类型之间的数学运算、比较、位操作等。
运算符重载使用operator关键字后跟要重载的运算符来实现。例如,+表示加法运算符,-表示减法运算符等。
运算符重载一般分为成员函数重载和全局函数重载
以下是一些常见的需要进行运算符重载的情况:
- 算术运算符:例如
+,-,*,/,%- 比较运算符:例如
==,!=,<,>,<=,>=- 赋值运算符:例如
=,+=,-=,*=,/=- 位操作运算符:例如
&,|,^- 下标操作符:
[]- 函数调用操作符:
()
对于每个需要进行重载的运算符,您可以根据需求定义适当的成员函数或非成员函数。成员函数形式在对象本身上调用该操作,而非成员函数形式将两个对象作为参数传递。
请注意,在进行运算符重载时,请遵循一些最佳实践和规则:
- 不要改变原始对象的状态(如果不是必要的)。
- 避免创建歧义或混乱的重载操作。
- 考虑使用友元函数来实现某些运算符重载,以便访问私有成员。
运算符重载是C++语言中的一项强大功能,可以提高代码的可读性和表达能力。
加号运算符重载
加号运算符(+)可以在C++中进行重载,使其适用于自定义类型的对象。要重载加号运算符,您可以使用成员函数或非成员函数的形式。
成员函数形式:本质为 p3 = p1.operator+(p2)
class MyClass {
public:MyClass operator+(MyClass& other) {// 在这里实现加法操作,并返回结果}
};
#include <iostream>class Complex {
private:double real;double imag;public:Complex(double r = 0.0, double i = 0.0) : real(r), imag(i) {}Complex operator+(const Complex& other) const {return Complex(real + other.real, imag + other.imag);}void display() const {std::cout << "(" << real << " + " << imag << "i)" << std::endl;}
};int main() {Complex c1(2.5, 3.7);Complex c2(1.8, -2.9);Complex sum = c1 + c2; // 使用重载的加号运算符sum.display(); // 输出:(4.3 + 0.8i)return 0;
}
全局函数形式:(友元函数访问私有成员)本质为 p3 = operator+(p1,p2)
class MyClass {
public:};MyClass operator+(const MyClass& obj1, const MyClass& obj2) {// 在这里实现加法操作,并返回结果}#include <iostream>class Complex {
private:double real;double imag;public:Complex(double r = 0.0, double i = 0.0) : real(r), imag(i) {}// 声明友元函数以便访问私有成员friend Complex operator+(const Complex& c1, const Complex& c2);void display() const {std::cout << "(" << real << " + " << imag << "i)" << std::endl;}
};Complex operator+(const Complex& c1, const Complex& c2) {return Complex(c1.real + c2.real, c1.imag + c2.imag);
}int main() {Complex c1(2.5, 3.7);Complex c2(1.8, -2.9);Complex sum = c1 + c2; // 使用重载的加号运算符sum.display(); // 输出:(4.3 + 0.8i)return 0;
}
俩个代码实现内容一样,主要一个是成员函数,一个全局函数,全局函数需要成为友元函数来访问类的私有数据成员。
同时运算符重载也可以发生函数重载
左移运算符重载
如果我们有一个person类,建立一个对象p,当我们想直接使用cout<<p<<endl;来输出对象p中的内容似乎并不能直接实现,C++并不认识这个类,也不知道如何输出。
这里我们就可以使用左移运算符重载了,与上面的加号运算符一样,左移运算符同样是以operato<<形式实现的,这里我们仍然可以分为成员函数重载和全局函数重载来分别实现一下。
当我们按照成员函数来写时,就会发现一个问题,首先你不能给自己传入p,即p.operator<<(p),然后我们再使用p.operator<<(cout),而这样简化的版本就是p<<cout,与我们想要的cout<<p相反了,所以我们不使用成员函数来实现左移运算符,而使用全局函数。
void operator<<(cout)
{
//简化完事 p << cout
}如果用全局函数首先要知道的事,cout是输出流对象,即ostream对象
使用operator<<(ostream &cout,person &p)进行函数重载,简化完事cout<<p
至于为什么不用void空值,而是ostream &,是因为,当你主函数使用函数重载输出后,如果返回的事空值,就不能继续追加输出,例如<<endl;补上换行,因为cout后面一直能连续使用<<是链式编程,需要返回的还是cout,即返回ostream输出流。
class preson
{
private:
string p_name;
int p_age;
public:
friend ostream & operator<<(ostream &cout,person &p);
}
ostream & operator<<(ostream &cout,person &p)
{cout<<"p_name"<<p.p_name<<"p_age"<<p._age<<endl;
}递增运算符重载
递增运算符重载,即要对++进行运算符重载
跟C++中的++a,a++一样,递增运算符重载也要分为前置递增和后置递增的重载
解决下述代码中几个重点问题
1、函数重载的返回类型就是自己建立的Integer类型是因为,如果有个对象num,当你想要实现对num++或者++num直接输出,类似于a=1;cout<<a++<<endl;的操作时,你需要返回Integer类型,否则返回空值是没有输出的
2、为什么前置递增返回值类型引用了,而后置递增返回值类型没有引用。
后置传递如果使用引用,那么值就错了,要返回递增前的值
这个主要是了解++运算符实现的本质
a=1;cout<<++(++a)<<endl; 这个是对的,说明前置运算符计算本质是引用,对一个数修改
cout<<(a++)++<<endl; 这个是错的,说明后置运算符计算本质是值传递,无法二次修改
3、下述代码偷懒了,应该演示一下++num,num++的输出,而不是使用成员函数getValue来实现,其实只要将左移运算符重载一下就可以了,按照已讲过的方法实现即可
#include <iostream>
using namespace std;class Integer {
private:int value;
public:Integer(int val) : value(val) {}// 前置递增运算符重载Integer& operator++() {++value;return *this;}// 后置递增运算符重载Integer operator++(int) {Integer temp(value);++value;return temp;}int getValue() const {return value;}
};int main() {Integer num1(5);cout << "初始值: " << num1.getValue() << endl;// 前置递增++num1;cout << "前置递增后的值: " << num1.getValue() << endl;// 后置递增Integer num2 = num1++;cout << "后置递增后的值: " << num2.getValue() << endl;cout << "num1当前的值: " << num1.getValue() << endl;return 0;
}
总结
本文主要对运算符重载进行了探讨,主要讲述了运算符重载分为成员函数重载和全局函数重载(友元函数重载)这样的操作,并举例加号,左移以及递增运算符的重载方法和一些注意事项。
通过上述的讲解,可以实现更多的运算法重载的方法,当然还有很多运算符重载值得我们探讨,本文讲述的内容也比较有限。
推荐学习博客 https://xxetb.xetslk.com/s/4GgGz6
相关文章:

C++面向对象学习笔记五
本文主要讲解运算符重载,由于白鳯大佬没有具体讲解,所以本文自行补充了运算符重载的相关知识 目录 文章目录 前言 运算符重载 加号运算符重载 左移运算符重载 递增运算符重载 总结 前言 本文主要对于运算符重载进行探讨,分别对于成员函数重…...

7-Zip 的使用技巧
7-Zip 是一款功能强大的压缩软件,它提供了多种使用技巧来帮助用户更高效地管理文件。以下是一些7-Zip的使用技巧: 1. 压缩文件:用户可以通过7-Zip将文件或文件夹压缩成.7z或其他支持的格式,以节省空间。 2. 解压文件:…...

德国储能项目锂电池储能集装箱突发火灾:安全挑战再引关注
2024年4月27日,德国尼尔莫尔商业区的一起锂电池储能集装箱火灾事件引起了全球关注。这起事故不仅导致两名消防员在救援过程中受伤,更暴露了储能系统在安全领域亟待解决的重要问题。 根据德国消防队的出警记录,火灾发生在晚上9点前不久。消防人…...
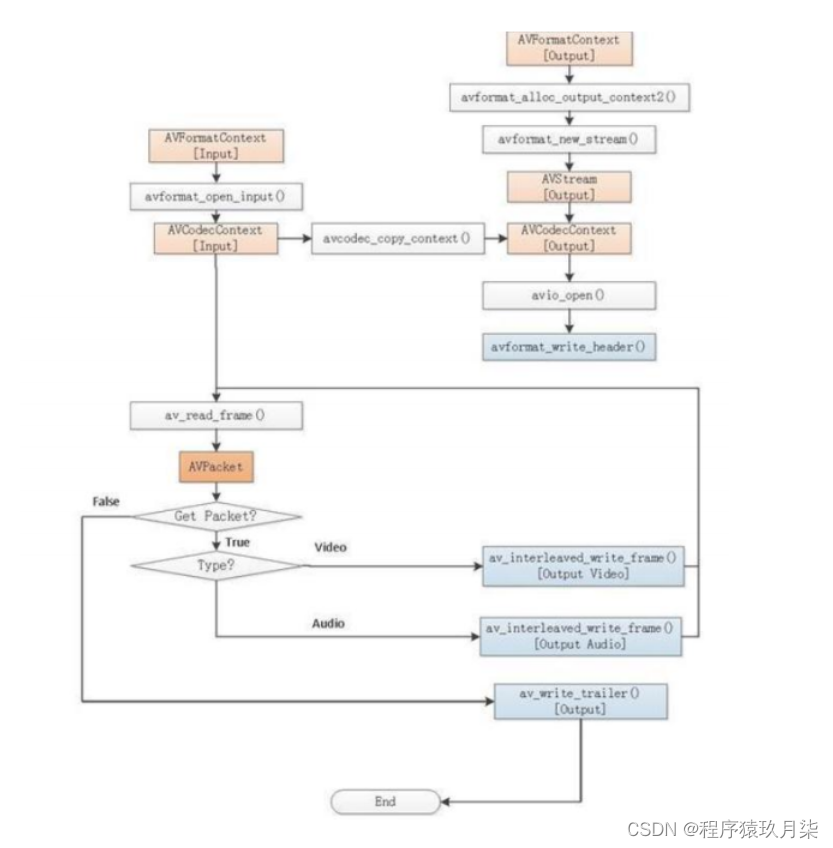
FFmpeg常用API与示例(二)—— 解封装与转封装
封装层 封装格式(container format)可以看作是编码流(音频流、视频流等)数据的一层外壳,将编码后的数据存储于此封装格式的文件之内。 封装又称容器,容器的称法更为形象,所谓容器,就是存放内容的器具,饮料是内容&…...
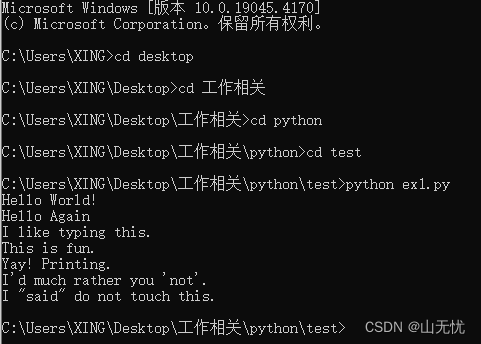
笨方法自学python(一)
我觉得python和c语言有很多相似之处,如果有c语言基础的话学习python也不是很难。这一系列主要是学习例题来学习python;我用的python版本是3.12 代码编辑器我用的是notepad,运行py程序用cmd 现在开始写第一个程序: print ("…...

centos7.9升级4.19内核
centos默认的内核版本是3.10 通过命令 uname -a 输出系统的详细信息 在部署k8s集群时使用默认的3.10版本的内核,容易出各种奇奇怪怪的问题、可以理解为docker和k8s与该内核版本不兼容,所以在部署k8s集群时,务必要升级内核,这里…...

神经网络模型与前向传播函数
1.概念 在神经网络中,模型和前向传播函数是紧密相关的概念。模型定义了网络的结构,而前向传播函数描述了数据通过网络的流动方式。以下是这两个概念的详细解释: 1.1 神经网络模型 神经网络模型是指构成神经网络的层、权重、偏置和连接的集…...

跟我学C++中级篇——内联补遗
一、内联引出的问题 在将一个内联变量定义到编译单元时,然后再按正常的方式使用时,编译会报一个错误“odr-used”。ODR,One Definition Rule,单一定义规则。在C/C程序中,变量的定义只能有一处,至于ODR的规…...

SLAM 面试题
持续完善 SLAM的基本概念和组成部分 描述一下什么是SLAM以及它的基本任务。 SLAM系统主要由哪些部分组成?SLAM的类型和算法 请解释滤波器SLAM(如粒子滤波)和图优化SLAM(如Google的Cartographer)之间的区别。 你如何区…...

csapp proxy lab part 1
host, hub, 路由器,和 交换机 当手机连接到局域网中时,它需要找到网络中的交换机(Switch)。这通常是通过 DHCP(动态主机配置协议)完成的。DHCP服务器负责向手机分配IP地址、子网掩码、网关地址等网络配置信…...
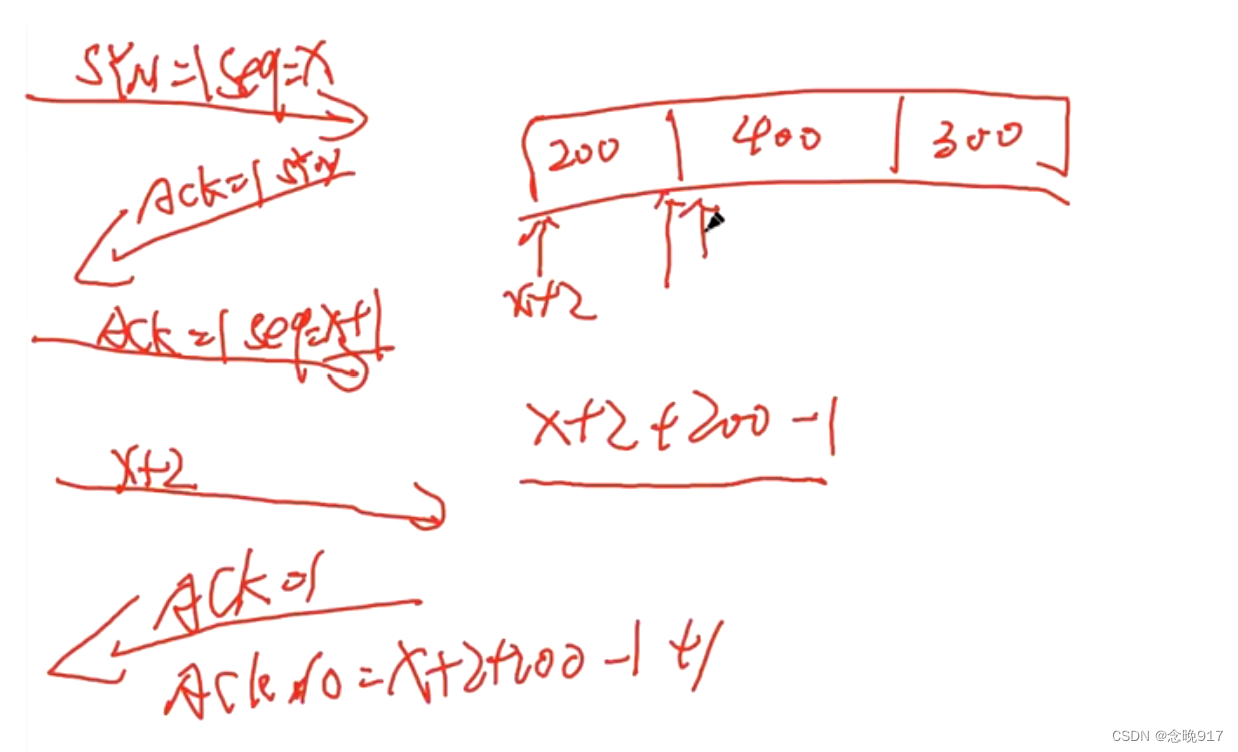
TCP三次握手四次挥手 UDP
TCP是面向链接的协议,而UDP是无连接的协议 TCP的三次握手 三次传输过程是纯粹的不涉及数据,三次握手的几个数据包中不包含数据内容。它的应用层,数据部分是空的,只是TCP实现会话建立,点到点的连接 TCP的四次挥手 第四…...
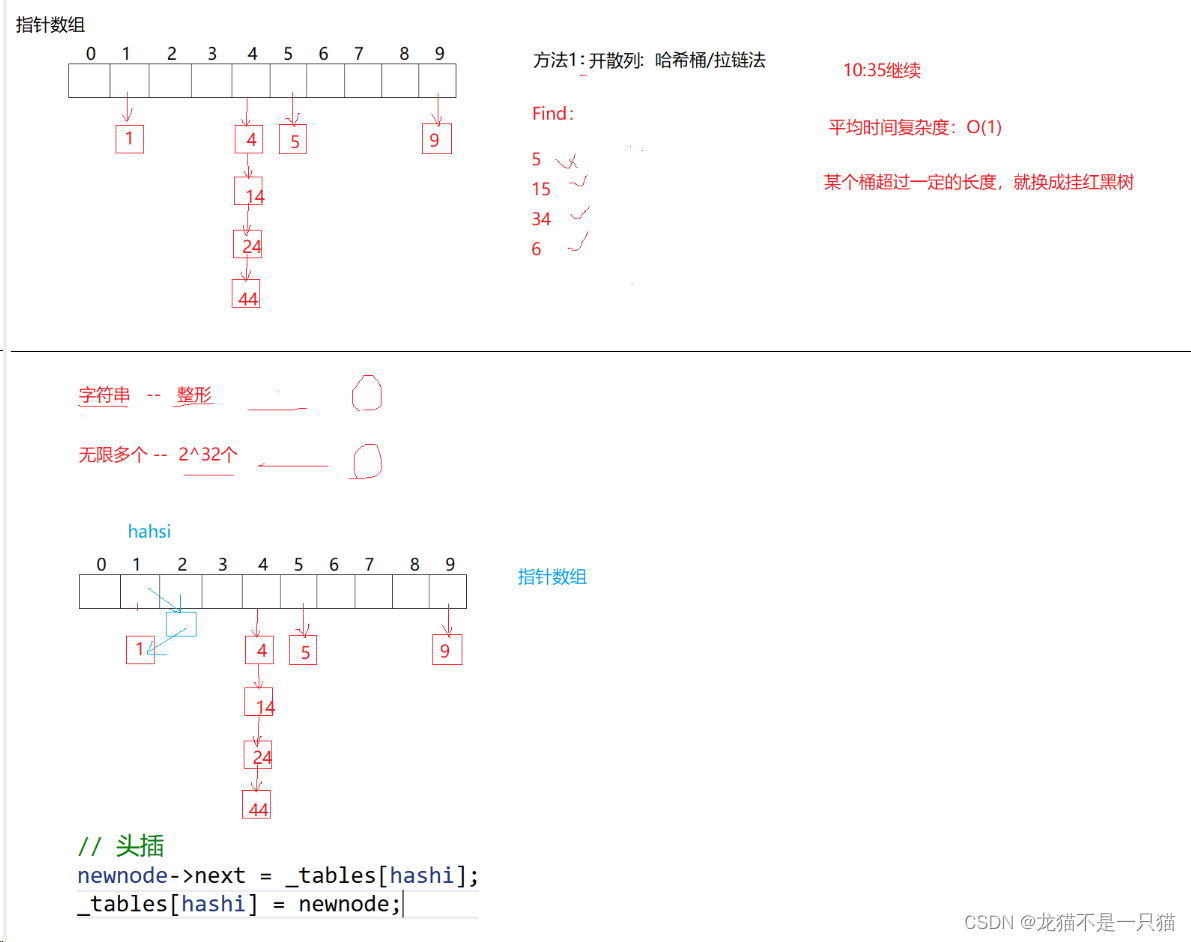
哈希表(unordered_set、unordered_map)
文章目录 一、unordered_set、unordered_map的介绍二、哈希表的建立方法2.1闭散列2.2开散列(哈希桶/拉链法) 三、闭散列代码(除留余数法)四、开散列代码(拉链法/哈希桶) 一、unordered_set、unordered_map的…...
Docker 加持的安卓手机:随身携带的知识库(一)
这篇文章聊聊,如何借助 Docker ,尝试将一台五年前的手机,构建成一个随身携带的、本地化的知识库。 写在前面 本篇文章,我使用了一台去年从二手平台购入的五年前的手机,K20 Pro。 为了让它能够稳定持续的运行…...
本地连接服务器Jupyter【简略版】
首先需要在你的服务器激活conda虚拟环境: 进入虚拟环境后使用conda install jupyter命令安装jupyter: 安装成功后先不要着急打开,因为需要设置密码,使用jupyter notebook password命令输入自己进入jupyter的密码: …...

sql 注入 1
当前在email表 security库 查到user表 1、第一步,知道对方goods表有几列(email 2 列 good 三列,查的时候列必须得一样才可以查,所以创建个临时表,select 123 ) 但是你无法知道对方goods表有多少列 用order …...
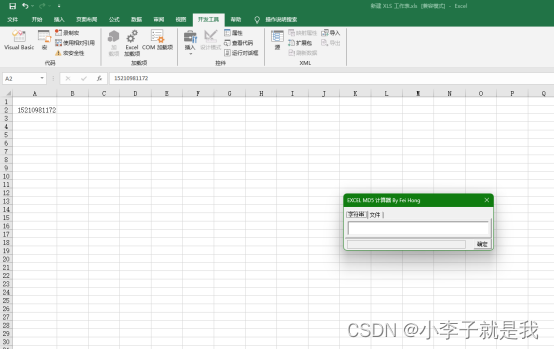
Excel中实现md5加密
1.注意事项 (1)在Microsoft Excel上操作 (2)使用完,建议修改的配置全部还原,防止有风险。 2.准备MD5宏插件 MD5加密宏插件放置到F盘下(直接F盘下,不用放到具体某一个文件夹下) 提示:文件在文章顶部&…...

写SQL的心得
1、统计 COUNT(列名) 和COUNT(*)均可,区别是前者只会统计非NULL。 2、where后面不能跟聚合函数,用的话应该在Having使用,因此需要先分组GroupBy where是基于行过滤,having是基于分…...
经典权限五张表功能实现
文章目录 用户模块(未使用框架)查询功能实现步骤代码 新增功能实现步骤代码 修改功能实现步骤代码实现 删除功能实现步骤代码实现 用户模块会了,其他两个模块与其类似 用户模块(未使用框架) 查询功能 这里将模糊查询和分页查询写在一起 实现步骤 前端࿱…...
实验八 Linux虚拟内存 实验9.1:统计系统缺页次数成功案例
运行环境: VMware17.5.1 build-23298084Ubuntu 16.04LTS ubuntu版本下载地址Linux-4.16.10 linux历史版本下载地址虚拟机配置:硬盘一般不少于40G就行 内核版本不同内核文件代码也有出入,版本差异性令c文件要修改,如若要在linux6.7…...

SD-WAN提升Microsoft 365用户体验
随着数字化时代的到来,SaaS应用如Microsoft 365已经成为各类企业的主流选择。在这一趋势下,企业需要以更加灵活、高效的方式使用Microsoft 365,以满足日益增长的业务需求。而传统的网络基础设施可能无法满足这一需求,因此…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...
