算法学习笔记(Nim游戏)
N i m Nim Nim游戏
n n n堆物品,每堆有 a i a_i ai个,每个玩家轮流取走任意一堆的任意个物品,但不能不取,取走最后一个物品的人获胜。
N i m Nim Nim游戏是一种经典的公平组合游戏。现在对它进行分析。
首先定义两个博弈中的状态:
- 必胜状态:先手必胜的状态。
- 必败状态:先手必败的状态。
对于这两个状态,我们可以知道:
- 没有后继状态的状态必然是必败状态。在这个状态中先手的是败者,因为他无法通过操作将游戏进行下去了。
- 一个状态是必胜状态当且仅当存在至少一个必败状态为它的后继状态。在这个状态中先手的人可以通过一次操作让对手在必败状态中先手。
- 一个状态的所有后继状态均为必胜状态,那么这个状态为必败状态。在这个状态中先手,无法避免让对方在必胜状态中先手。
回到 N i m Nim Nim游戏:
在 N i m Nim Nim游戏中,一个很显然的必败状态就是所有物品堆中物品的数量都为 0 0 0,即 [ 0 , 0 , . . . , 0 ] [0, 0, ..., 0] [0,0,...,0]。这个状态也是最终态。可以知道,在最终态时,所有物品堆中的物品数量的异或和是等于 0 0 0的,我们不妨假设状态和物品数量的异或和有关系。
证明有关:
一个非 0 0 0的异或和,产生最高位的 1 1 1总需要有奇数个数字来提供对应位置的 1 1 1。而我们为了消去这个 1 1 1,可以选择任意一个提供这个 1 1 1的数字,使其二进制中该位上的数字为 0 0 0,而且修改最高位为 0 0 0后得到的数字永远小于原来的数字,也就是说,我们可以任意修改其他位上的数字从而使得全部物品数量的异或和为 0 0 0。
而对于一个为 0 0 0的异或和,假设存在一个 b ≠ a i b \not = a_i b=ai使得我们将 a i a_i ai修改为 b b b后,异或和还是为 0 0 0,则有 0 ⊕ a i ⊕ b = 0 0 \oplus a_i \oplus b = 0 0⊕ai⊕b=0,为了使这个式子成立 b b b就要等于 a i a_i ai,与假设违背。
换句话说,对于一个物品数量异或和不为 0 0 0的状态,我们可以通过一次操作将物品数量的异或和修改为 0 0 0,而对于一个物品数量异或和为 0 0 0的操作,我们无法只通过一次操作保持物品数量的异或和不变。
从上可以得出,在 N i m Nim Nim游戏中,物品数量异或和为 0 0 0的状态是必败状态,物品数量异或和不为 0 0 0的状态是必胜状态。
接下来看例题:
【模板】Nim 游戏
【模板】Nim 游戏
题目描述
甲,乙两个人玩 nim 取石子游戏。
nim 游戏的规则是这样的:地上有 n n n 堆石子(每堆石子数量小于 1 0 4 10^4 104),每人每次可从任意一堆石子里取出任意多枚石子扔掉,可以取完,不能不取。每次只能从一堆里取。最后没石子可取的人就输了。假如甲是先手,且告诉你这 n n n 堆石子的数量,他想知道是否存在先手必胜的策略。
输入格式
本题有多组测试数据。
第一行一个整数 T T T ( T ≤ 10 T\le10 T≤10),表示有 T T T 组数据
接下来每两行是一组数据,第一行一个整数 n n n,表示有 n n n 堆石子, n ≤ 1 0 4 n\le10^4 n≤104。
第二行有 n n n 个数,表示每一堆石子的数量.
输出格式
共 T T T 行,每行表示如果对于这组数据存在先手必胜策略则输出 Yes,否则输出 No。
样例 #1
样例输入 #1
2
2
1 1
2
1 0
样例输出 #1
No
Yes
根据刚才的推论,我们只需要计算所有数字的异或和,就可以得出先手时处在必胜状态还是必败状态。用 O ( n ) O(n) O(n)的复杂度即可得出最后的胜负结果。
#include<bits/stdc++.h>
using namespace std;void solve()
{int n; cin >> n;int ans = 0;for(int i = 1; i <= n; ++i){int x; cin >> x;ans ^= x;}cout << (ans ? "Yes" : "No") << '\n';
}int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int _; cin >> _;while(_--) solve();return 0;
}
相关文章:
)
算法学习笔记(Nim游戏)
N i m Nim Nim游戏 n n n堆物品,每堆有 a i a_i ai个,每个玩家轮流取走任意一堆的任意个物品,但不能不取,取走最后一个物品的人获胜。 N i m Nim Nim游戏是一种经典的公平组合游戏。现在对它进行分析。 首先定义两个博弈中的状…...
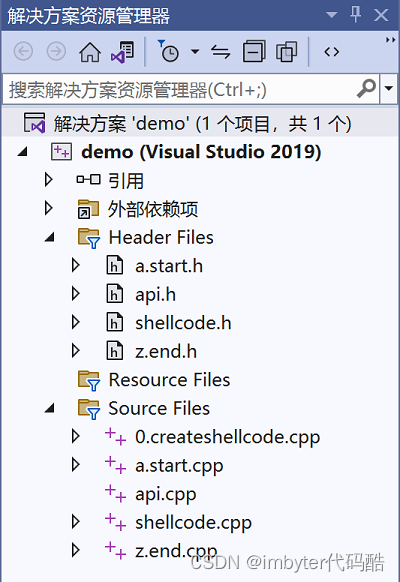
第13节 第二种shellcode编写实战(2)
在第二种shellcode编写实战(1)的基础上,新增加一个CAPI类,将所有用到的函数都在这个类中做动态调用的处理,这样使得整个shellcode功能结构更加清晰。 1. 新建类CAPI(即api.h和api.cpp两个文件): api.h&…...
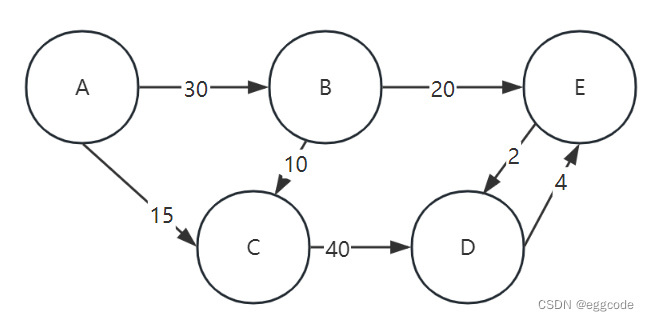
【QuikGraph】C#调用第三方库实现迪杰斯特拉(Dijkstra)算法功能
QuikGraph库介绍 项目地址:https://github.com/KeRNeLith/QuikGraph QuikGraph为.NET提供了通用的有向/无向图数据结构和算法。 QuikGraph提供了深度优先搜索、广度优先搜索、A*搜索、最短路径、k最短路径,最大流量、最小生成树等算法。 QuikGraph最初…...

查看ubuntu当前路径的剩余存储空间
要查看Ubuntu当前路径所在磁盘分区的剩余存储空间,应该使用df命令,而不是du命令,因为df命令能显示磁盘分区的使用情况,包括总容量、已用空间和可用空间。为了使输出更易于阅读,可以加上-h选项。如果你还想知道特定挂载…...

利用预训练模型和迁移学习打造智能狗门
引言 在深度学习的世界里,预训练模型和迁移学习是两个强大的概念,它们允许我们利用已有的模型和知识来解决新的问题。在本博客中,我们将探索如何使用预训练的模型来创建一个智能狗门,这个系统将能够识别狗并允许它们进入…...

常用Linux命令详细总结
一、文档编辑、过滤、查看命令 1、cp 复制文件和目录 -a 复制文件并保持文件属性 -d 若源文件为链接文件,则复制链接文件属性而非文件本身 -i 覆盖文件前提示,如果不要提示,在命令前加上\ -r 递归复制,通常用于目录的复制 …...

基于SpringBoot的竹宣非遗宣传网站
摘要 随着互联网的普及和数字化时代的到来,竹编等非物质文化遗产的保护与传承面临新的机遇和挑战。该研究旨在使用SpringBoot后端框架与Vue前端框架,构建一个竹编非遗宣传网站,通过丰富的展示形式和交互体验,提升公众对竹编这一非…...

怎么清理服务器的C盘?
有时候我们经常会遇到C盘被占满的情况,C盘被占满的原因有很多,下面我们就来分析下有可能导致C盘占满的原因: 第一种情况:中毒 打开服务器任务管理器选择进程,并且勾选显示所有用户的进程,我们可以点击映像…...

动态规划----股票买卖问题(详解)
目录 一.买卖股票的最佳时机: 二.买卖股票的最佳时机含冷冻期: 三.买卖股票的最佳时期含⼿续费: 四.买卖股票的最佳时机III: 五.买卖股票的最佳时机IV: 买卖股票的最佳时机问题介绍:动态规划买卖股票的最佳时机是一个经典的…...

Unity射线检测不到MeshCollider的原因
当我们构建的模型是单面模型时,就会出现射线检测不到MeshCollider的问题,对于渲染,我们可以Cull Off来实现双面渲染,而在射线检测时,Unity提供了一个API来控制是否检测背面:Physics.queriesHitBackfaces 案…...
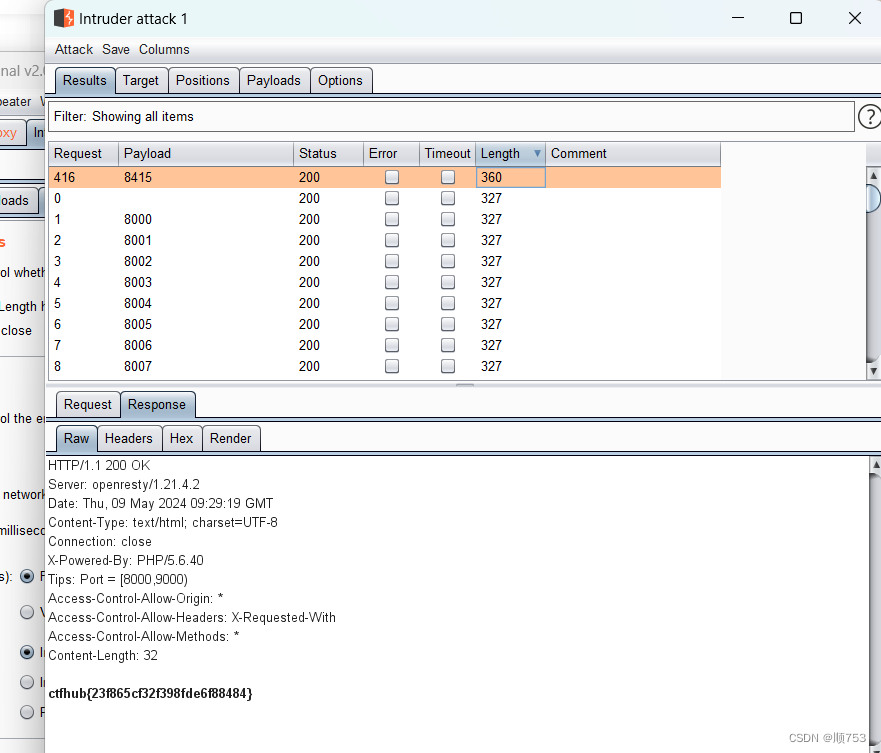
ssrf初步
一,简介 全称:Server-Side Request Forgery(中文:服务器端请求伪造) 攻击者从服务端发起请求,让服务器连接任意外部系统,从而泄露敏感数据。主要利用各种协议的请求伪造,例如php协…...

linux 安装 mangodb 并设置服务开机自启
1、下载 wget http://mosquitto.org/files/source/mosquitto-1.6.8.tar.gz 2、解压 tar -zxvf mosquitto-1.6.8.tar.gz 3、编译安装cd mosquitto-1.6.8 make sudo make install4、在当前目录。进入mosquitto服务文件存放的文件夹 cd service/systemd可以看到3个文件 点击read…...
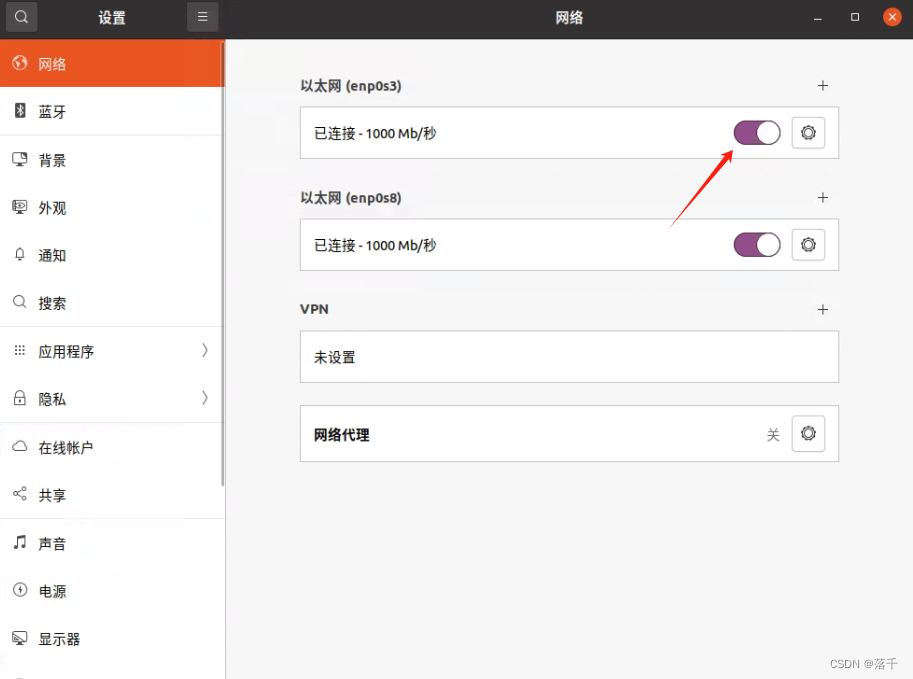
Virtualbox7.0.10+Ubuntu20.04网络配置
虚拟机部署在服务器上时,需要进行网络配置,使虚拟机和服务器在同网段下,以保证内网的终端可以访问到虚拟机 1. 设置虚拟机 打开虚拟机设置,选择“网络”,将网卡设为桥接网卡 注:设置前,需要先…...

设计模式之服务定位器模式
想象一下,你的Java应用是一座庞大的迷宫,里面藏着无数宝贵的服务宝藏,而你正需要一张精确的藏宝图来指引方向,迅速找到并利用这些宝藏。服务定位器模式,正是这样一张神奇的地图,它帮你动态定位并获取应用中…...
冯喜运:5.12黄金回撤继续上涨,下周原油走势分析
【黄金消息面分析】:本周,黄金市场迎来了自4月中旬以来的最佳单周表现。周五(3月9日),金价攀升至2360.54美元/盎司,涨幅0.62%,而纽约商品交易所6月交割的黄金期货价格上涨1.5%,收报2…...
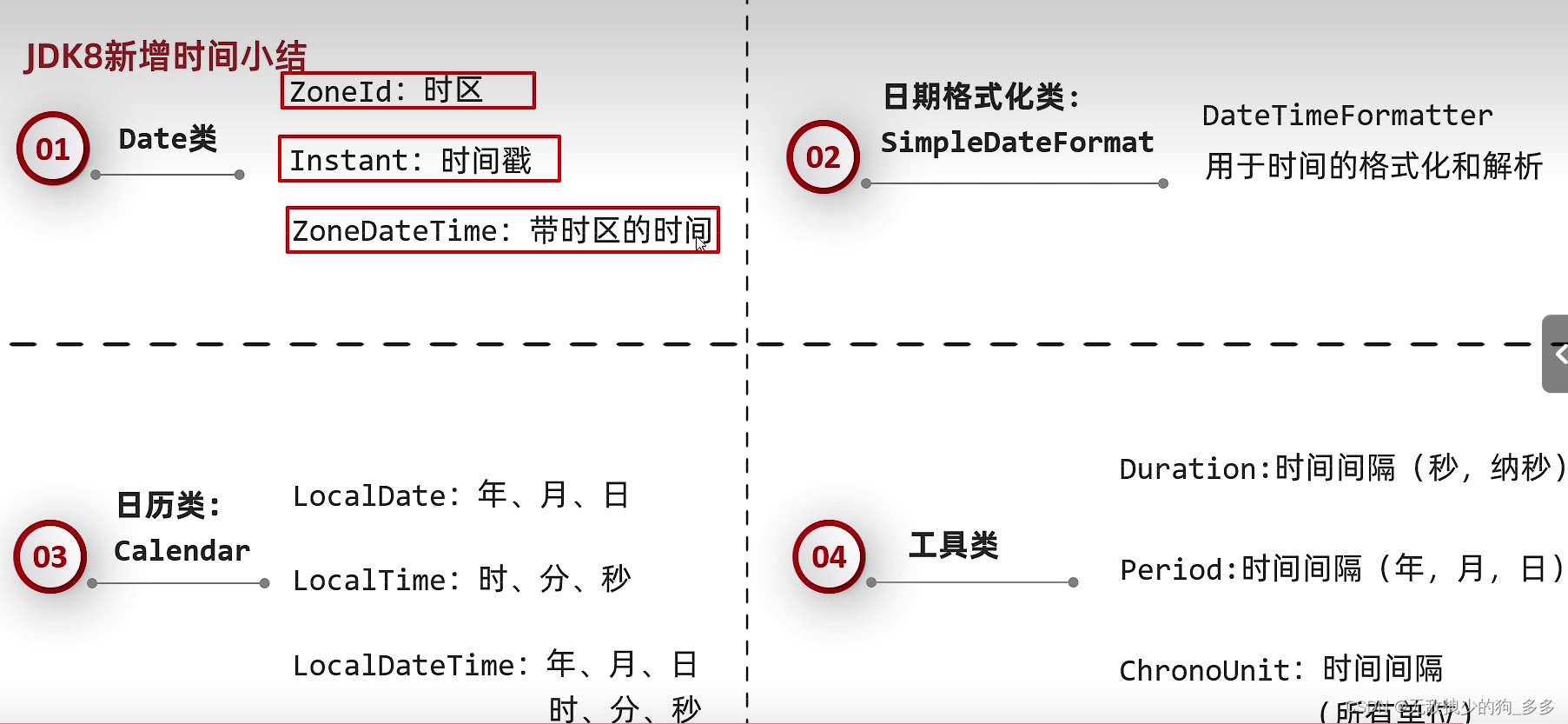
JavaEE企业级开发中常用的JDK7和JDK8的时间类
JDK7时间类 全世界的时间有一个统一的计算标准 在同一条经线上的时间是一样的 格林威治时间 简称GMT 计算核心 地球自转一天是24小时 太阳直射正好是12小时 但是误差太大 现在用原子钟来代替 用铯原子震动的频率来计算时间,作为世界的标准时间UTC 中国标准时间…...

leetcode 2316.统计无向图中无法互相到达点对数
思路:并查集 其实就是连通块的一个变形题目,一般的连通块题目要我们求的是连通个数,或者能不能到达,这里反过来问了。 首先,我们用dfs也是可以做到的,在dfs中统计每一个连通块的个数,然后用乘…...

WPS二次开发系列:如何使用WPS返回的FileUri
作者持续关注 WPS二次开发专题系列,持续为大家带来更多有价值的WPS开发技术细节,如果能够帮助到您,请帮忙来个一键三连,更多问题请联系我(QQ:250325397) 目录 什么是FileUri 在SDK中的使用场景 打开文档时…...

python删除一个文件夹所有文件
在Python中,可以使用os模块来删除一个文件夹中的所有文件,但保留文件夹本身。以下是一个简单的例子: import osdef delete_files_in_folder(folder_path):for filename in os.listdir(folder_path):file_path os.path.join(folder_path, fi…...

overflow:hidden对解决外边距塌陷的个人理解
外边距塌陷: 子元素的上外边距大于父元素的上外边距,导致边距折叠,取两者之间最大值,即子元素外边距,导致父元素上外边距失效。 解决办法:在父元素样式添加overflow:hidden;或者border:1px solid black;(不…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...
