C++ 容器(五)——Set操作
一、Set容器定义
set 是一个有序关联容器,其中的元素按照升序排列,且不允许重复元素。 set 中的元素是唯一的,即任意两个元素不能相等。
1、set 可以用来对元素进行排序,因为它会自动对元素进行有序排列。
2、set 可以用来去重,当我们需要对一个容器中的元素进行去重操作时,可以使用 set 来实现。
3、set 可以用来判断一个元素是否存在于容器中。
二、Set容器操作
1)创建Set容器
std::set<int> mySet; // 创建一个空的set
std::set<int> mySet2 = {1, 2, 3}; // 创建一个具有初始值的set
std::set<int> mySet3(mySet2); // 创建一个与另一个set相同的set
扩展:如果Set初始化元素需要从Vector数组直接赋值,可以使用迭代器,例如:
set<int> mySet(vec.begin(),vec.end());2)添加元素
mySet.insert(5); // 向set中插入元素
std::set<int> anotherSet = {1, 2, 3}; // 向set中插入一段迭代器范围内的元素
mySet.insert相关文章:
——Set操作)
C++ 容器(五)——Set操作
一、Set容器定义 set 是一个有序关联容器,其中的元素按照升序排列,且不允许重复元素。 set 中的元素是唯一的,即任意两个元素不能相等。 1、set 可以用来对元素进行排序,因为它会自动对元素进行有序排列。 2、set 可以用来去重,当我们需要对一个容器中的元素进行去重操…...

【数字IC设计】芯片设计中的RDC
RDC问题定义 在芯片设计中,RDC是reset domain crossing 的缩写,类似于CDC(clock domain crossing),由于现在SOC芯片是有很多ECUs组成,为了使整个系统能够快速从复位中恢复, 用户希望SOC里面每个ECU模块都可以有自己独立的异步复位信号,这样可以在出问题的时候只复位有错…...

spark history server异常
现象:spark 日志文件突然新增了很多.hprof文件, 查找日志spark配置参数spark_log_dir进入日志目录: 查看historyServer日志: Spark Command: /usr/lib/jvm/java-1.8.0/bin/java -cp /opt/apps/JINDOSDK/jindosdk-current/lib/*:/…...
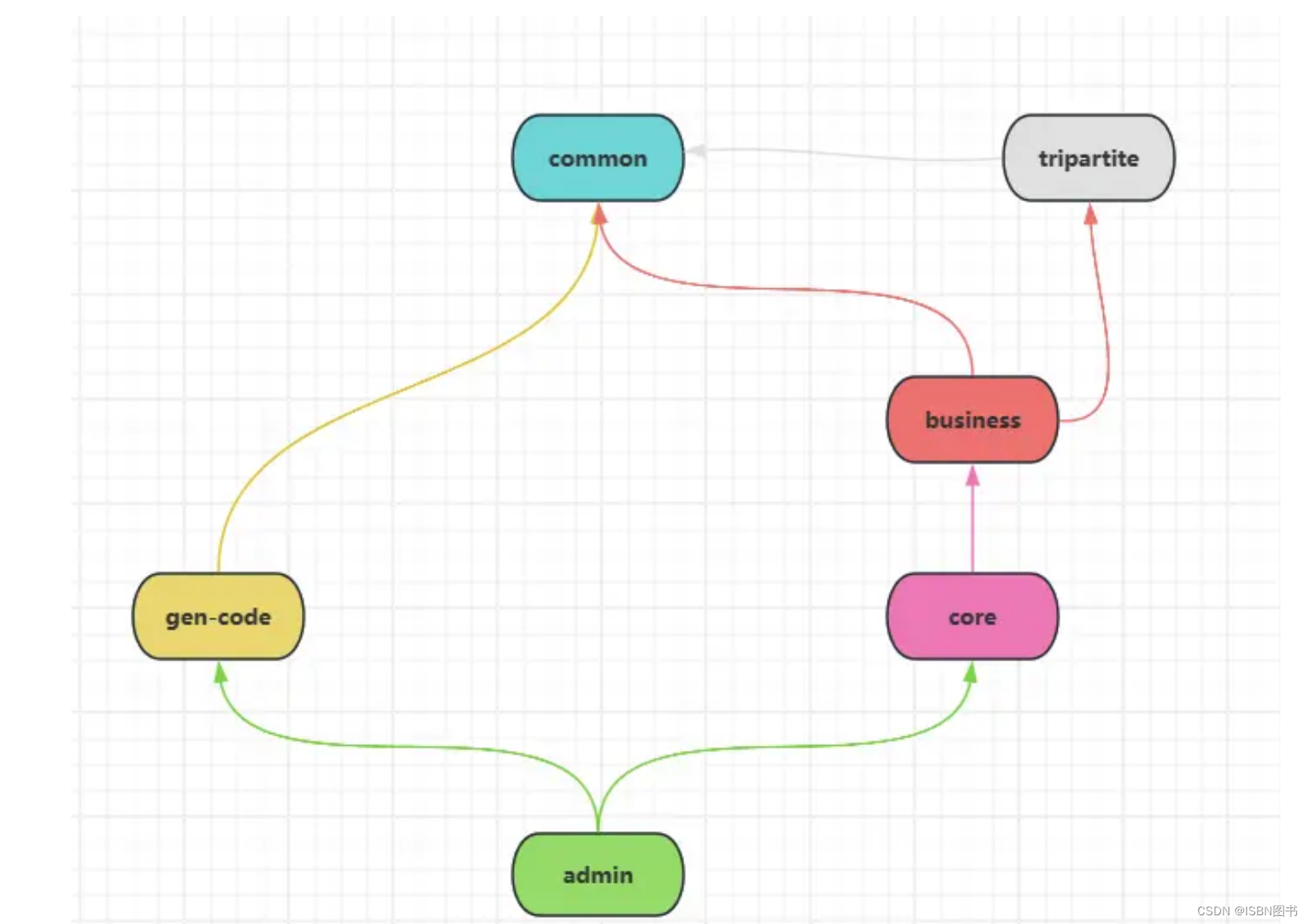
一个优秀 Maven 项目,各 Model 间最佳继承设计方案
1.单一职责原则 (Single Responsibility Principle): 每个模块应该专注于执行一个清晰且明确定义的功能,遵循单一职责原则,以降低模块的复杂性。 2.高内聚性 (High Cohesion): 模块内的组件和类应该紧密相关,共同实现模块的目标。高内聚性…...

MATLAB概述
文章目录 目录结构搜索路径高频命令clearclf/closeclc/homewho/whosformatsave/loadcd/pwdhelp/docsprintf/fprintf/disp tips MATLAB [1] 是美国 MathWorks公司出品的商业 数学软件,用于算法开发、数据可视化、数据分析以及 数值计算的高级技术计算语言和交互式…...

Redis5.0的Stream数据结构
Redis 5.0中引入的Stream数据结构是一种新的、持久化的、可查询的、可扩展的消息队列服务。它可以被视为一个日志或消息队列,由一个有序的、不断增长的日志序列来存储事件流数据。以下是关于Redis 5.0 Stream数据结构的详细解释: 一、Stream数据结构概述…...

避坑指南!RK3588香橙派yolov5生成RKNN模型!
地址1,转换模型 地址2,转换模型 地址3,解决ppa 下载k2 本文目录 一、将.pt模型转为onnx模型文件。(Windows)二、将.onnx模型转为.rknn模型文件。(Linux)三、将.rknn模型部署到开发板RK3588中…...
)
算法学习笔记(Nim游戏)
N i m Nim Nim游戏 n n n堆物品,每堆有 a i a_i ai个,每个玩家轮流取走任意一堆的任意个物品,但不能不取,取走最后一个物品的人获胜。 N i m Nim Nim游戏是一种经典的公平组合游戏。现在对它进行分析。 首先定义两个博弈中的状…...
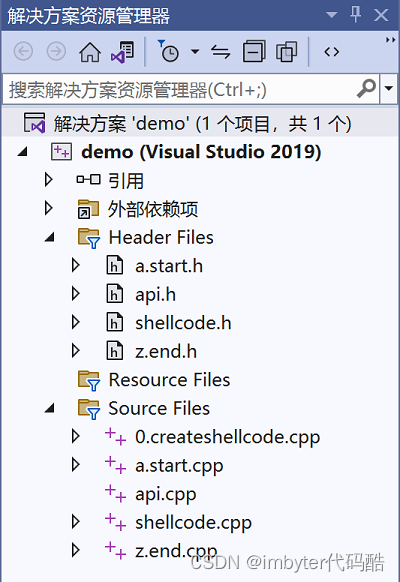
第13节 第二种shellcode编写实战(2)
在第二种shellcode编写实战(1)的基础上,新增加一个CAPI类,将所有用到的函数都在这个类中做动态调用的处理,这样使得整个shellcode功能结构更加清晰。 1. 新建类CAPI(即api.h和api.cpp两个文件): api.h&…...
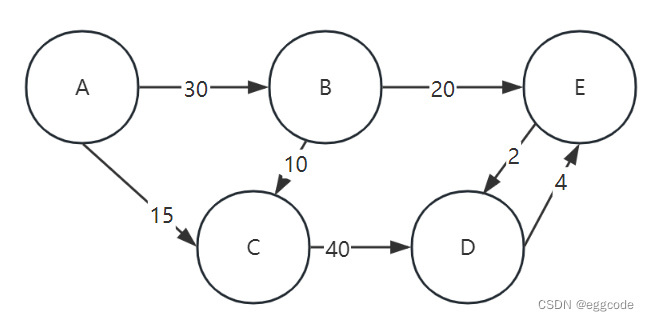
【QuikGraph】C#调用第三方库实现迪杰斯特拉(Dijkstra)算法功能
QuikGraph库介绍 项目地址:https://github.com/KeRNeLith/QuikGraph QuikGraph为.NET提供了通用的有向/无向图数据结构和算法。 QuikGraph提供了深度优先搜索、广度优先搜索、A*搜索、最短路径、k最短路径,最大流量、最小生成树等算法。 QuikGraph最初…...

查看ubuntu当前路径的剩余存储空间
要查看Ubuntu当前路径所在磁盘分区的剩余存储空间,应该使用df命令,而不是du命令,因为df命令能显示磁盘分区的使用情况,包括总容量、已用空间和可用空间。为了使输出更易于阅读,可以加上-h选项。如果你还想知道特定挂载…...

利用预训练模型和迁移学习打造智能狗门
引言 在深度学习的世界里,预训练模型和迁移学习是两个强大的概念,它们允许我们利用已有的模型和知识来解决新的问题。在本博客中,我们将探索如何使用预训练的模型来创建一个智能狗门,这个系统将能够识别狗并允许它们进入…...

常用Linux命令详细总结
一、文档编辑、过滤、查看命令 1、cp 复制文件和目录 -a 复制文件并保持文件属性 -d 若源文件为链接文件,则复制链接文件属性而非文件本身 -i 覆盖文件前提示,如果不要提示,在命令前加上\ -r 递归复制,通常用于目录的复制 …...

基于SpringBoot的竹宣非遗宣传网站
摘要 随着互联网的普及和数字化时代的到来,竹编等非物质文化遗产的保护与传承面临新的机遇和挑战。该研究旨在使用SpringBoot后端框架与Vue前端框架,构建一个竹编非遗宣传网站,通过丰富的展示形式和交互体验,提升公众对竹编这一非…...

怎么清理服务器的C盘?
有时候我们经常会遇到C盘被占满的情况,C盘被占满的原因有很多,下面我们就来分析下有可能导致C盘占满的原因: 第一种情况:中毒 打开服务器任务管理器选择进程,并且勾选显示所有用户的进程,我们可以点击映像…...

动态规划----股票买卖问题(详解)
目录 一.买卖股票的最佳时机: 二.买卖股票的最佳时机含冷冻期: 三.买卖股票的最佳时期含⼿续费: 四.买卖股票的最佳时机III: 五.买卖股票的最佳时机IV: 买卖股票的最佳时机问题介绍:动态规划买卖股票的最佳时机是一个经典的…...

Unity射线检测不到MeshCollider的原因
当我们构建的模型是单面模型时,就会出现射线检测不到MeshCollider的问题,对于渲染,我们可以Cull Off来实现双面渲染,而在射线检测时,Unity提供了一个API来控制是否检测背面:Physics.queriesHitBackfaces 案…...
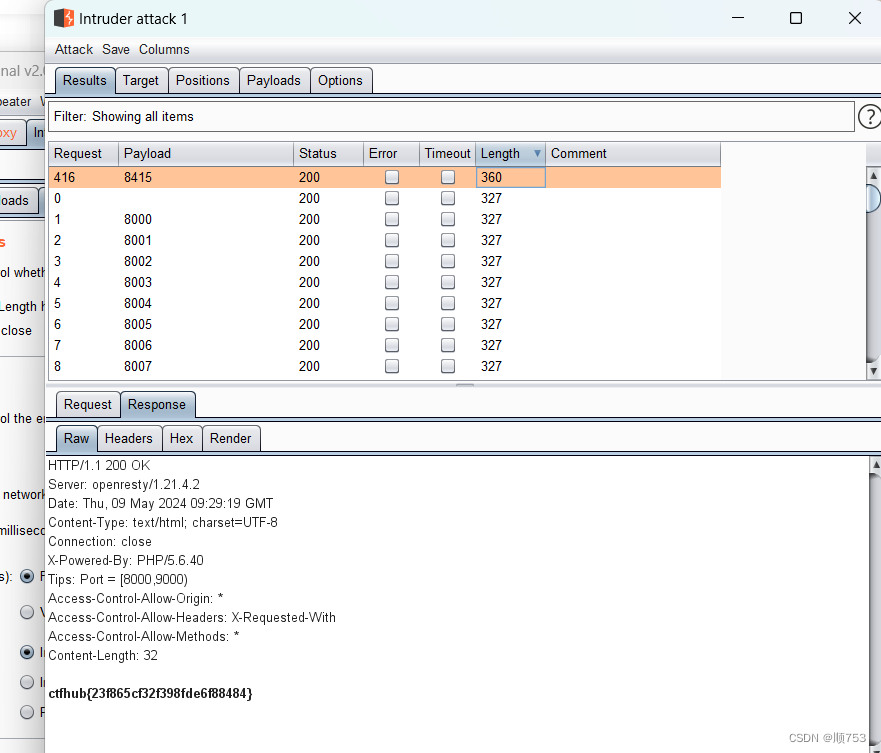
ssrf初步
一,简介 全称:Server-Side Request Forgery(中文:服务器端请求伪造) 攻击者从服务端发起请求,让服务器连接任意外部系统,从而泄露敏感数据。主要利用各种协议的请求伪造,例如php协…...

linux 安装 mangodb 并设置服务开机自启
1、下载 wget http://mosquitto.org/files/source/mosquitto-1.6.8.tar.gz 2、解压 tar -zxvf mosquitto-1.6.8.tar.gz 3、编译安装cd mosquitto-1.6.8 make sudo make install4、在当前目录。进入mosquitto服务文件存放的文件夹 cd service/systemd可以看到3个文件 点击read…...
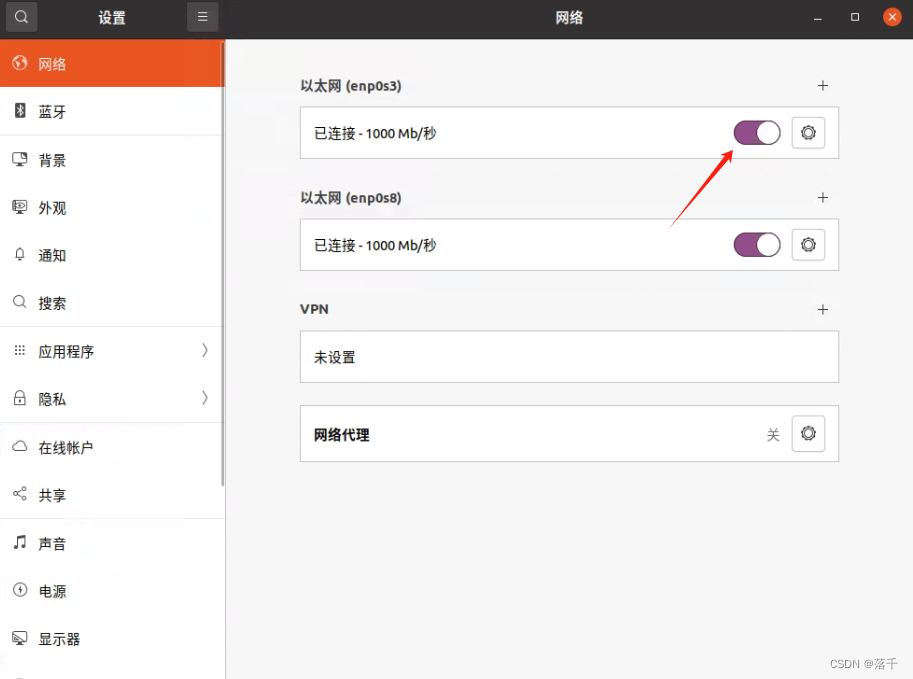
Virtualbox7.0.10+Ubuntu20.04网络配置
虚拟机部署在服务器上时,需要进行网络配置,使虚拟机和服务器在同网段下,以保证内网的终端可以访问到虚拟机 1. 设置虚拟机 打开虚拟机设置,选择“网络”,将网卡设为桥接网卡 注:设置前,需要先…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
