哈希表Hash table
哈希表是根据关键码的值而直接进行访问的数据结构。
数组就是⼀张哈希表。
哈希表中关键码就是数组的索引下标,然后通过下标直接访问数组中的元素,如下图所示:
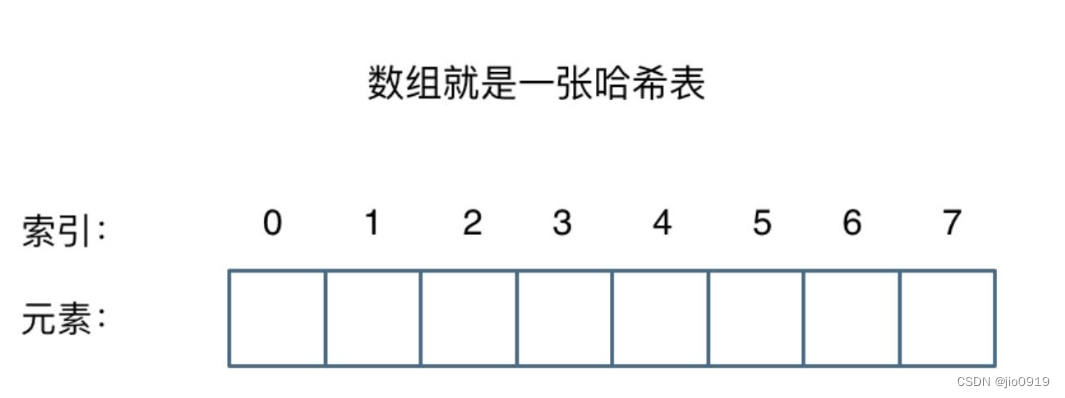
那么哈希表能解决什么问题呢,一般哈希表都是用来快速判断⼀个元素是否出现集合里。
例如要查询一个名字是否在这所学校里。
要枚举的话时间复杂度是O(n),但如果使用哈希表的话,只需要O(1)就可以做到。
我们只需要初始化把这所学校里学生的名字都存在哈希表里,在查询的时候通过索引直接就可以知道这位同学在不在这所学校里了。
哈希函数
哈希函数,把学生的姓名直接映射为哈希表上的索引,然后就可以通过查询索引下标快速知道这位同学是否在这所学校里了。
哈希函数如下图所示,通过hashCode把名字转化为数值,一般hashcode是通过特定编码方式,可以将其他数据格式转化为不同的数值,这样就把学生名字映射为哈希表上的索引数字了。

如果hashCode得到的数值大于哈希表的大小了,也就是大于tableSize了,怎么办呢?
此时为了保证映射出来的索引数值都落在哈希表上,我们会在再次对数值做一个取模的操作,就要我们就保证了学生姓名一定可以映射到哈希表上了。
此时问题又来了,哈希表我们刚刚说过,就是一个数组。
如果学生的数量大于哈希表的大小怎么办,此时就算哈希函数计算的再均匀,也避免不了会有几位学生的名字同时映射到哈希表同⼀个索引下标的位置。
接下来哈希碰撞登场
哈希碰撞
如图所示,小李和小王都映射到了索引下标 1 的位置,这一现象叫做哈希碰撞。

一般哈希碰撞有两种解决方法,拉链法和线性探测法。
拉链法
刚刚小李和小王在索引 1 的位置发生了冲突,发生冲突的元素都被存储在链表中。这样我们就可以通过索引找到小李和小王了

(数据规模是dataSize,哈希表的大小为tableSize)
其实拉链法就是要选择适当的哈希表的大小,这样既不会因为数组空值而浪费大量内存,也不会因为链表太长而在查找上浪费太多时间。
线性探测法
使用线性探测法,⼀定要保证tableSize大于dataSize。我们需要依靠哈希表中的空位来解决碰撞问题。
例如冲突的位置,放了小李,那么就向下找⼀个空位放置小王的信息。所以要求tableSize⼀定要⼤于dataSize,要不然哈希表上就没有空置的位置来存放冲突的数据了。如图所示:

常见的三种哈希结构
当我们想使用哈希法来解决问题的时候,我们一般会选择如下三种数据结构。
1.数组
2.set(集合)
3.map(映射)
这里数组就没啥可说的了,我们来看⼀下set和map。

std::unordered_set底层实现为哈希表,std::set和std::multiset的底层实现是红黑树,红黑树是⼀种平衡二叉搜索树,所以key值是有序的,但key不可以修改,改动key值会导致整棵树的错乱,所以只能删除和增加。

std::unordered_map底层实现为哈希表,std::map和std::multimap的底层实现是红黑树。同理,std::map和std::multimap的key也是有序的
当我们要使用集合来解决哈希问题的时候,优先使用unordered_set,因为它的查询和增删效率是最优的,如果需要集合是有序的,那么就用set,如果要求不仅有序还要有重复数据的话,那么就用multiset。
那么再来看一下map,在map是一个key value的数据结构,map中,对key是有限制,对value没有限制的,因为key的存储方式使用红黑树实现的。
虽然std::set、std::multiset的底层实现是红黑树,不是哈希表,std::set、std::multiset使用红黑树来索引和存储,不过给我们的使用方式,还是哈希法的使用方式,即key和value。所以使用这些数据结构来解决映射问题的方法,我们依然称之为哈希法。map也是⼀样的道理。
有效的字母异位词

就是判断 s 和 t 是否是由相同的字符组成
数组其实就是⼀个简单哈希表,而且这道题目中字符串只有小写字符,那么就可以定义一个数组,来记录字符串 s 里字符出现的次数。
定义⼀个数组叫做record用来上记录字符串s里字符出现的次数。
需要把字符映射到数组也就是哈希表的索引下标上,因为字符a到字符z的ASCII是26个连续的数值,所以字符a映射为下标0,相应的字符z映射为下标25。
再遍历字符串s的时候,只需要将s[i] - ‘a’所在的元素做+1操作即可,并不需要记住字符a的ASCII,只要求出一个相对数值就可以了。这样就将字符串s中字符出现的次数,统计出来了。
那看一下如何检查字符串 t 中是否出现了这些字符,同样在遍历字符串t的时候,对 t 中出现的字符映射哈希表索引上的数值再做 -1 的操作。
那么最后检查一下,record数组如果有的元素不为零0,说明字符串 s 和 t 一定是谁多了字符或者谁少了字符,return false。
class solution
{
public:bool cmp(string s, string t){int record[26] = { 0 };for (int i = 0; i < s.size(); ++i){record[s[i] - 'a']++;}for (int i = 0; i < t.size(); ++i){record[t[i] - 'a']--;}for (int i = 0; i < 26; ++i){if (record[i] != 0){return false;}}return true;}
};两个数组的交集
题意:给定两个数组,编写一个函数来计算它们的交集。


这道题目,主要要学会使用一种哈希数据结构:unordered_set,这个数据结构可以解决很多类似的问题。
注意题目特意说明:输出结果中的每个元素一定是唯一的,也就是说输出的结果的去重的,同时可以不考虑输出结果的顺序
思路如图所示:

代码:
# include <iostream>
# include <vector>
# include <unordered_set>
using namespace std;int main()
{vector<int> nums1;vector<int> nums2;int n;int m;cin >> n >> m;int x;for (int i = 0; i < n; ++i){cin >> x;nums1.push_back(x);}for (int i = 0; i < m; ++i){cin >> x;nums2.push_back(x);}unordered_set<int> result;unordered_set<int> nums(nums1.begin(), nums1.end());for (int num : nums2){if (nums.find(num) != nums.end())result.insert(num);}}快乐数



# include <iostream>
# include <vector>
# include <unordered_set>
using namespace std;int made(int x)
{int sum = 0;while (x > 0){sum = sum + (x % 10) * (x % 10);x = x / 10;}return sum;
}bool cmp(int x)
{unordered_set<int> last;int s = x;while (1){s = made(s);if (last.find(s) == last.end()){if (s == 1)return true;last.insert(s);}else{return false;}}
}int main()
{int n;cin >> n;cout << bool(n);
}两数之和

首先我在强调一下什么时候使用哈希法,当我们需要查询一个元素是否出现过,或者一个元素是否在集合里的时候,就要第一时间想到哈希法。
本题呢,我就需要一个集合来存放我们遍历过的元素,然后在遍历数组的时候去询问这个集合,某元素是否遍历过,也就是是否出现在这个集合。
那么我们就应该想到使用哈希法了。
因为本地,我们不仅要知道元素有没有遍历过,还要知道这个元素对应的下标,需要使用key value结构来存放,key来存元素,value来存下标,那么使用map正合适。
再来看⼀下使用数组和set来做哈希法的局限。
1.数组的大小是受限制的,而且如果元素很少,而哈希值太大会造成内存空间的浪费。
2.set是⼀个集合,里面放的元素只能是⼀个key,而两数之和这道题目,不仅要判断y是否存在,而且还要记录y的下标位置,因为要返回x和y的下标。所以set也不能用
此时就要选择另⼀种数据结构:map,map是⼀种key value的存储结构,可以用key保存数值,用value在保存数值所在的下标。

这道题目中并不需要key有序,选择std::unordered_map效率更高!
接下来需要明确两点:
1.map用来做什么
2.map中key和value分别表示什么
map用来存放我们访问过的元素
数组中的元素作为key,有key对应的就是value,value用来存下标。
# include <iostream>
# include <vector>
# include <unordered_map>
using namespace std;int main()
{int num[100];int n;int target;cin >> n >> target;unordered_map<int, int> map;for (int i = 0; i < n; ++i){cin >> num[i];}for (int i = 0; i < n; ++i){if (map.find(target - num[i]) != map.end()){auto iter = map.find(target - num[i]);cout << i << iter->second;}map.insert(pair<int, int>{ num[i], i });}
}四数相加II

例如:
输⼊:
A = [1, 2]
B = [ -2, -1]
C = [-1, 2]
D = [ 0, 2]
输出:
2

本题是使用哈希法的经典题目,这道题目是四个独立的数组,只要找到A[i] + B[j] + C[k] + D[l] = 0就可以,不用考虑有重复的四个元素相加等于0的情况。

# include <iostream>
# include <vector>
# include <unordered_map>
using namespace std;int main()
{int n;cin >> n;int a[500];int b[500];int c[500];int d[500];for (int i = 0; i < n; ++i){cin >> a[i];}for (int i = 0; i < n; ++i){cin >> b[i];}for (int i = 0; i < n; ++i){cin >> c[i];}for (int i = 0; i < n; ++i){cin >> d[i];}unordered_map<int, int>map;for (int i : a){for (int j : b){map[i + j]++;}}int count = 0;for (int i : c){for (int j : d){if (map.find(0 - i - j) != map.end())count = count + map[0 - i - j];}}cout << count;
}相关文章:

哈希表Hash table
哈希表是根据关键码的值而直接进行访问的数据结构。 数组就是⼀张哈希表。 哈希表中关键码就是数组的索引下标,然后通过下标直接访问数组中的元素,如下图所示: 那么哈希表能解决什么问题呢,一般哈希表都是用来快速判断⼀个元素是…...

jdk8新特性----Lambda表达式
一、介绍 1、简介 Java的Lambda表达式是Java 8引入的一个特性,它支持函数式编程,允许将函数作为方法的参数或返回值,从而简化了匿名内部类的使用,并提供了对并行编程的更好支持。 2、语法 Lambda表达式的使用前提是存在一…...
在STM32中用寄存器方式点亮流水灯
文章目录 实验资料一、对寄存器的理解1.通俗认识寄存器2.深入了解寄存器(1)端口配置低寄存器(配置0到7引脚的寄存器)(2)端口配置高寄存器(配置8到15引脚) 3.GPIO口的功能描述 二、配…...
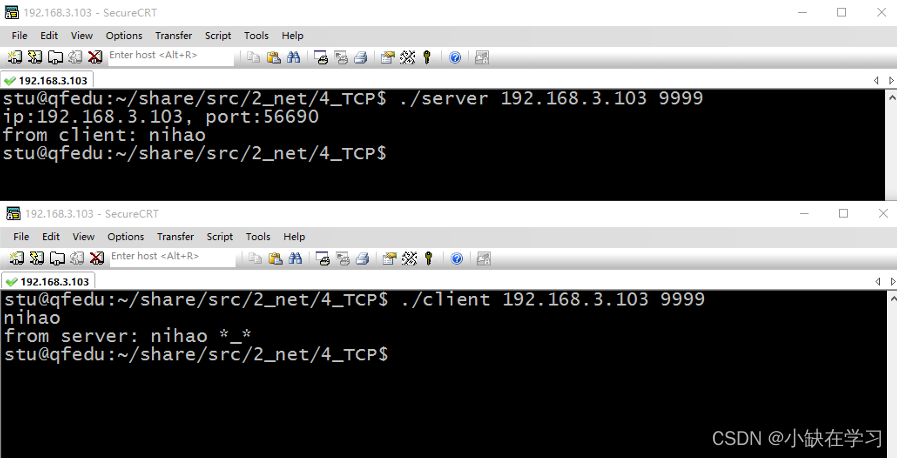
TCP(TCP客户端、服务器如何通信)
一、TCP介绍 TCP的特点: 面向连接的协议:TCP是一种可靠的、面向连接的协议,在通信之前需要建立连接,以确保数据的可靠传输。这意味着在传输数据之前,发送方和接收方之间需要建立一条可靠的连接通道。流式协议&#x…...
)
pdf 文件版面分析--PyMuPDF (python 文档解析提取)
1.介绍 PyMuPDF 和Fitz 是用于Python中处理PDF文件的相关模块。Fitz是P有MuPDF的字模块。提供一个简化和封装版本的P有MuPDF功能。 关系: PyMuPDF: 提供广泛的功能,用于操作PDF文档, 包括方便的高级函数与底层操作Fitz &#x…...

sql update 多表关联 inner join
当您需要更新一个表或者多个表中的数据,而多个表又存在关联时,可以使用 INNER JOIN 子句将多个表关联起来,并使用 SET更新。 格式如下: UPDATE table1 INNER JOIN table2 ON table1.column1 table2.column1 SET table1.column2…...

【OceanBase诊断调优】—— 租户资源统计项及其查询方法
本文主要介绍 OceanBase 数据库中租户资源统计项及其查询方法。 适用版本 OceanBase 数据库 V4.1.x、V4.2.x 版本。 CPU 资源统计项 逻辑 CPU 使用率(线程处理请求的时间占比)。 通过虚拟表 __all_virtual_sysstat 在 SYS 系统租户下,查看…...

【一键录音,轻松转换:用Python打造个性化音频记录工具】
在数字化时代,音频记录已成为日常学习、工作和娱乐不可或缺的一部分。想象一下,只需简单按下几个键,即可随时随地捕捉灵感,记录会议要点,或是珍藏孩子的童言稚语。本文将引领您步入Python编程的奇妙世界,展示如何借助几个强大的库,构建一个既简单又实用的音频录制及转换…...

Java类与对象(一)
类的定义与使用 在Java中使用关键字class定义一个类,格式如下: class 类名{// 成员变量/字段/属性//成员方法/行为 }Java中类和c语言中的结构体有点类似, 在Java中类名一般采用大驼峰(每个首字母大写)的形式…...

python中的装饰器,例子说明
在Python中,嵌套装饰器是指在一个函数上应用多个装饰器。每个装饰器都可以为函数添加一些特定的功能。以下是一个稍微复杂一些的例子,我们将创建一个记录日志和验证权限的嵌套装饰器。 ### 例子:记录日志和权限验证的嵌套装饰器 假设我们正…...

Leetcode经典题目之用队列实现栈
P. S.:以下代码均在VS2019环境下测试,不代表所有编译器均可通过。 P. S.:测试代码均未展示头文件stdio.h的声明,使用时请自行添加。 目录 1、题目展示2、题目分析3、完整代码演示4、结语 1、题目展示 前面我们了解过如何实现队列…...

DBSCAN聚类算法
目录 背景DBSCAN算法DBSCAN算法原理DBSCAN算法基本步骤DBSCAN算法调优DBSCAN算法优缺点参考文献 背景 如果有车队在某一片区域经常规律性作业,现在要让你来绘制这一片的路网,你会选择让一辆车从头到尾把所有路网跑一遍还是基于历史轨迹点通过技术手段构…...

【tauri】安装
https://blog.csdn.net/freewebsys/article/details/136092092 1 安装nodejs curl -sL https://deb.nodesource.com/setup_18.x -o nodesource_setup.sh sudo bash nodesource_setup.sh sudo apt install nodejs # 查看版本 node -v2 安装webkit2 sudo apt update sudo apt i…...

(Java)心得:LeetCode——19.删除链表的倒数第 N 个节点
一、原题 给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。 示例 1: 输入:head [1,2,3,4,5], n 2 输出:[1,2,3,5]示例 2: 输入:head [1], n 1 输出:[]示例 3&…...
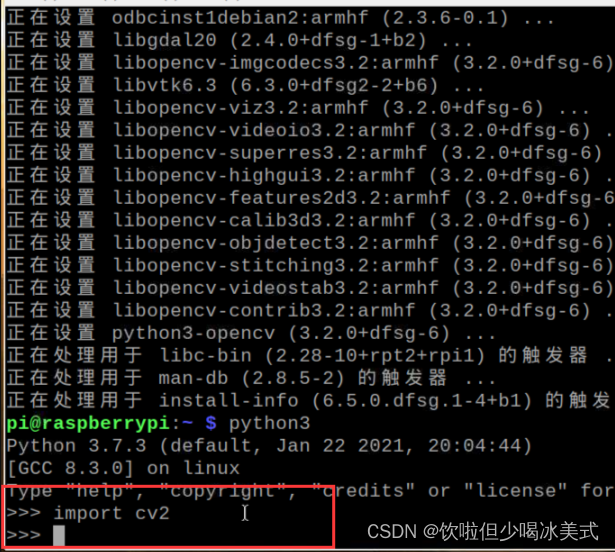
树莓派安装opencv
安装opencv 上述步骤完成后,输入以下代码(基于python3) sudo apt-get install python3-opencv -y不行的话,试试换源,然后 sudo apt-get update成功! 测试opencv是否安装成功 输入 python3 然后再输入 import cv2 没有报错就…...

bert 的MLM框架任务-梯度累积
参考:BEHRT/task/MLM.ipynb at ca0163faf5ec09e5b31b064b20085f6608c2b6d1 deepmedicine/BEHRT GitHub class BertConfig(Bert.modeling.BertConfig):def __init__(self, config):super(BertConfig, self).__init__(vocab_size_or_config_json_fileconfig.get(vo…...
Nginx配置/.well-known/pki-validation/
当你需要在Nginx上配置.well-known/pki-validation/时,这通常是为了支持SSL证书的自动续订或其他验证目的。以下是配置步骤: 创建目录结构: 在你的网站根目录下创建一个名为.well-known的目录(SSL证书申请之如何创建/.well-known/…...
)
iOS LQG开发框架(持续更新)
基本规则 开发便利性为前提,妥协性能可维护性为前提可读性MVC各部分职责一定要清晰,controll类里面功能尽量抽离成helper,功能一定要清晰,这个非常重要,对代码可读性提升非常高方法内部尽量使用局部变量,最…...

Python 自动化脚本系列:第3集
21. 使用 cryptography 自动化文件加密 Python 的 cryptography 库提供了一种安全的方式,使用对称加密算法对文件进行加密和解密。你可以自动化加密和解密文件的过程来保护敏感数据。 示例:文件加密和解密 假设你想使用对称加密算法加密一个文件&…...
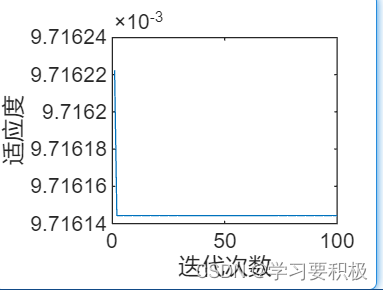
Matlab-粒子群优化算法实现
文章目录 一、粒子群优化算法二、相关概念和流程图三、例题实现结果 一、粒子群优化算法 粒子群优化算法起源于鸟类觅食的经验,也就是一群鸟在一个大空间内随机寻找食物,目标是找到食物最多的地方。以下是几个条件: (1) 所有的鸟都会共享自己的位置以及…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...
