(Java)心得:LeetCode——19.删除链表的倒数第 N 个节点
一、原题
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
示例 1:
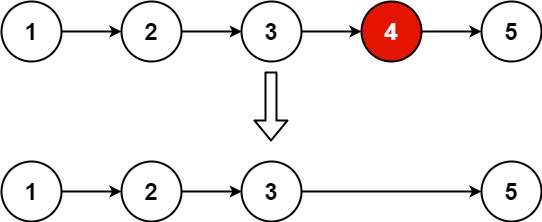
输入:head = [1,2,3,4,5], n = 2 输出:[1,2,3,5]
示例 2:
输入:head = [1], n = 1 输出:[]
示例 3:
输入:head = [1,2], n = 1 输出:[1]
二、心得
这一题是数据结构中的链表,我学的时候是用的 C/C++ 语言,这里尝试了一下用 Java 语言来编,整体的结构是互通的,只是一些表达方式上有些出入罢了~o(* ̄▽ ̄*)ブ
直接看代码:
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public ListNode removeNthFromEnd(ListNode head, int n) {// 定义一个节点,next 指向链表的头节点ListNode dummy = new ListNode(0, head);int length = getLength(head);ListNode cur = dummy;//for (int i = 1; i < length - n + 1; ++i) {cur = cur.next;}// 删除第 n 个节点,(本质为跳过倒数第 n 个节点,将倒数第 n - 1 个节点连接到倒数第 n + 1 个节点的 next 上)cur.next = cur.next.next; // 翻译一下就是: 倒数第 n + 1 个节点的 next 等于 (倒数第 n 个节点的 next)[即倒数第 n - 1 个节点]ListNode ans = dummy.next;return ans;}// 将 head 依次存入链表,获取链表的长度public int getLength(ListNode head) {int length = 0;while (head != null) {length ++;head = head.next;}return length;}
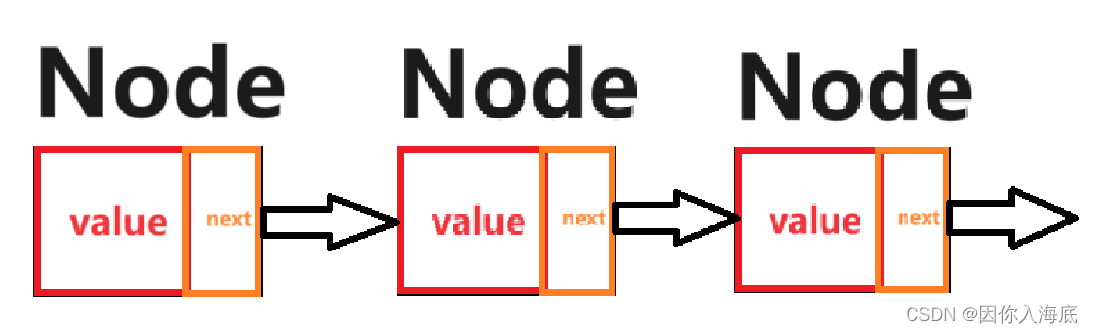
}先简单解释一下链表的基本结构:节点。节点,包括值 value,指向下一节点的指针 next 。至于要不要指向上一节点的指针 front ,根据需求设置,这里不考虑。
这里再解释一下 cur.next = cur.next.next; :

继续学习ing~
相关文章:

(Java)心得:LeetCode——19.删除链表的倒数第 N 个节点
一、原题 给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。 示例 1: 输入:head [1,2,3,4,5], n 2 输出:[1,2,3,5]示例 2: 输入:head [1], n 1 输出:[]示例 3&…...
树莓派安装opencv
安装opencv 上述步骤完成后,输入以下代码(基于python3) sudo apt-get install python3-opencv -y不行的话,试试换源,然后 sudo apt-get update成功! 测试opencv是否安装成功 输入 python3 然后再输入 import cv2 没有报错就…...

bert 的MLM框架任务-梯度累积
参考:BEHRT/task/MLM.ipynb at ca0163faf5ec09e5b31b064b20085f6608c2b6d1 deepmedicine/BEHRT GitHub class BertConfig(Bert.modeling.BertConfig):def __init__(self, config):super(BertConfig, self).__init__(vocab_size_or_config_json_fileconfig.get(vo…...
Nginx配置/.well-known/pki-validation/
当你需要在Nginx上配置.well-known/pki-validation/时,这通常是为了支持SSL证书的自动续订或其他验证目的。以下是配置步骤: 创建目录结构: 在你的网站根目录下创建一个名为.well-known的目录(SSL证书申请之如何创建/.well-known/…...
)
iOS LQG开发框架(持续更新)
基本规则 开发便利性为前提,妥协性能可维护性为前提可读性MVC各部分职责一定要清晰,controll类里面功能尽量抽离成helper,功能一定要清晰,这个非常重要,对代码可读性提升非常高方法内部尽量使用局部变量,最…...

Python 自动化脚本系列:第3集
21. 使用 cryptography 自动化文件加密 Python 的 cryptography 库提供了一种安全的方式,使用对称加密算法对文件进行加密和解密。你可以自动化加密和解密文件的过程来保护敏感数据。 示例:文件加密和解密 假设你想使用对称加密算法加密一个文件&…...
Matlab-粒子群优化算法实现
文章目录 一、粒子群优化算法二、相关概念和流程图三、例题实现结果 一、粒子群优化算法 粒子群优化算法起源于鸟类觅食的经验,也就是一群鸟在一个大空间内随机寻找食物,目标是找到食物最多的地方。以下是几个条件: (1) 所有的鸟都会共享自己的位置以及…...

python 新特性
文章目录 formatted字符串字面值formatted字符串支持 字符串新方法变量类型标注二进制表示中数字为1的数量统计字典的三个方法新增mapping属性函数zip()新增strict参数dataclass字典合并match 语法 formatted字符串字面值 formatted字符串是带有’f’字符前缀的字符串…...
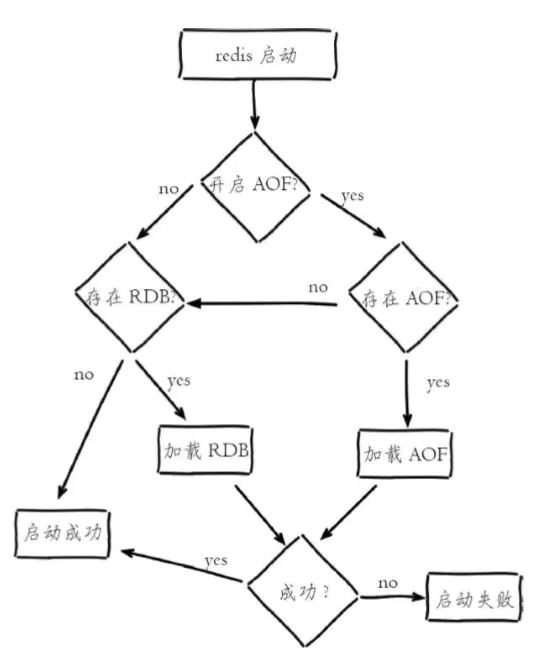
十一、Redis持久化-RDB、AOF
Redis提供了两种持久化数据的方式。一种是RDB快照,另一种是AOF日志。RDB快照是一次全量备份,AOF日志是连续的增量备份。RDB快照是以二进制的方式存放Redis中的数据,在存储上比较紧凑;AOF日志记录的是对内存数据修改的指令文本记录…...
)
Oracle闪回数据库【Oracle闪回技术】(二)
理解Oracle闪回级别【Oracle闪回技术】(一)-CSDN博客 Oracle默认是不开启闪回数据库的。如果开启闪回数据库的前提条件是,开启Oracle归档模式并启用闪回恢复区。 因为闪回日志文件存放在闪回恢复区中,如果在RAC环境下,必须将闪回恢复区存储在集群文件或者ASM文件中。 一…...

简单负载均衡
题目描述 某工程师为了解决服务器负载过高的问题,决定使用多个服务器来分担请求消息。 现给定 k 台服务器(编号从 1 到 k),以及一批请求消息的信息,格式为到达时刻 负载大小,消息说明: 每个时刻…...
Portforge:一款功能强大的轻量级端口混淆工具
关于Portforge Portforge是一款功能强大的轻量级端口混淆工具,该工具使用Crystal语言开发,可以帮助广大研究人员防止网络映射,这样一来,他人就无法查看到你设备正在运行(或没有运行)的服务和程序了。简而言…...

1.8. 离散时间鞅-无界停时定理与随机游走
无界停时定理与随机游走 无界停时定理与随机游走1. 无界停时定理1.1. 一致可积1.2. 非一致可积2. 应用于随机游动-鞅方法2.1. 随机游走构造的鞅2.2. 对称简单随机游走无界停时定理与随机游走 1. 无界停时定理 本节给出一致可积下鞅的无界停时定理,说明一致可积下鞅的停止过程…...
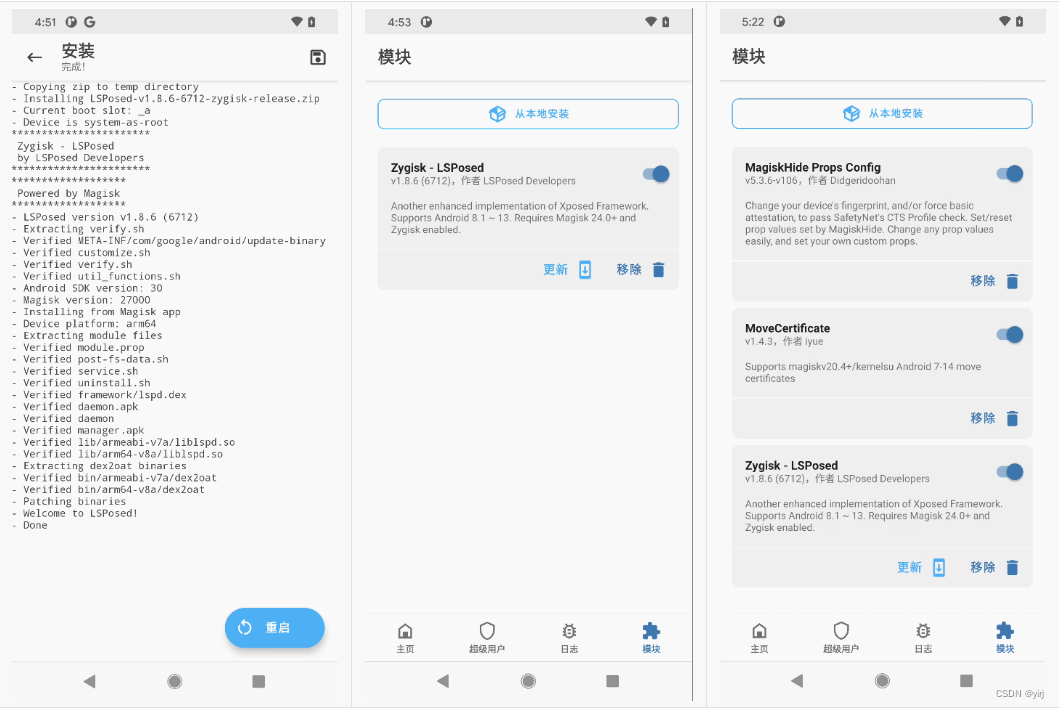
Google Pixel4手机刷机+Root+逆向环境详细教程
Google Pixel4手机刷机Root逆向环境配置详细教程 刷机工具下载 Windows10、Google Pixel4手机当前安卓10系统、adb工具、要刷的谷歌原生的Android11最新刷机包、安装google usb驱动、美版临时twrp-3.6.0_11-0-flame.img和美版永久twrp-installer-3.6.0_11-0-flame.zip、Magis…...
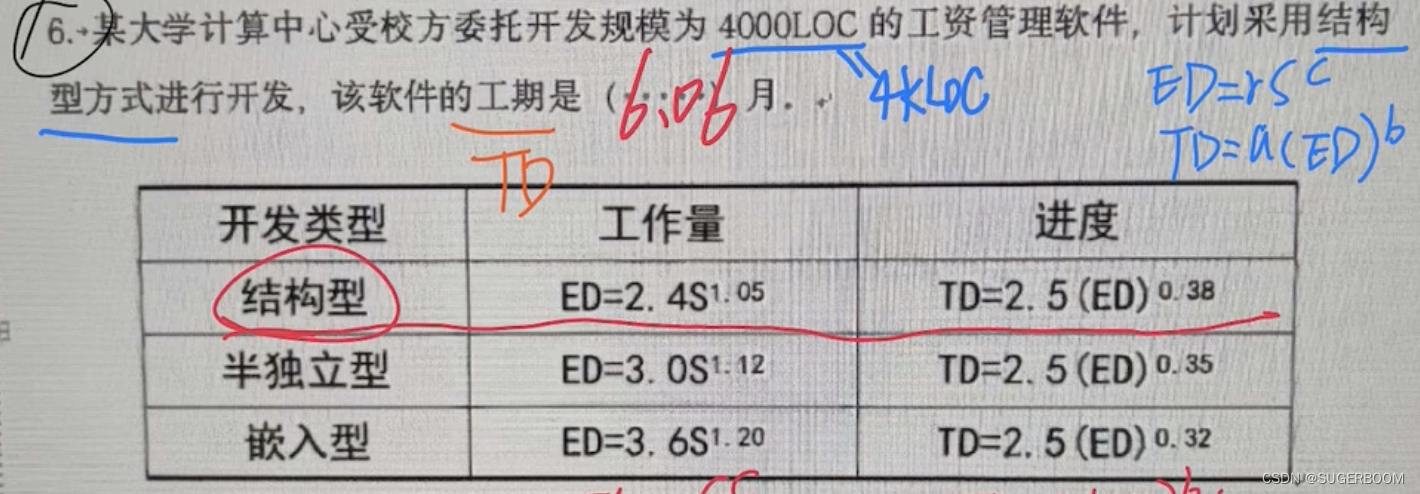
IT项目管理-小题计算【太原理工大学】
1.合同总价问题 问承包商的利润是? 实际利润目标利润(目标成本-实际成本)*卖方分担比例 解:10 000(100 000 - 90 000)* 0.2 12 000(元) 实际成本有时也写作最终成本,问承…...
ARP欺骗使局域网内设备断网
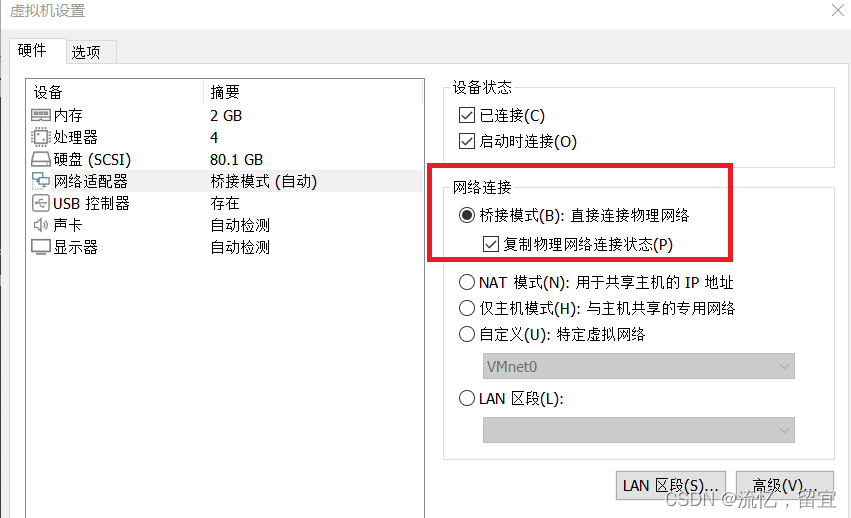
一、实验准备 kali系统:可使用虚拟机软件模拟 kali虚拟机镜像链接:https://www.kali.org/get-kali/#kali-virtual-machines 注意虚拟机网络适配器采用桥接模式 局域网内存在指定断网的设备 二、实验步骤 打开kali系统命令行:ctrlaltt可快…...

Android动画(四):PathMeasure实现路径动画
文章概览 1 PathMeasure概述2 实现路径加载动画3 实现箭头加载动画4 实现操作成功动画 本系列将介绍以下内容: Android动画 1 PathMeasure概述 PathMeasure是一个单独的类,其全部源码如下(请详细研读注释): package…...

HTTP 连接详解
概述 世界上几乎所有的 HTTP 通信都是由 TCP/IP 承载的,客户端可以打开一条TCP/IP连接,连接到任何地方的服务器。一旦连接建立,客户端和服务器之间交换的报文就永远不会丢失、受损或失序 TCP(Transmission Control Protocol&…...
练习题(2024/5/12)
1二分查找 给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。 示例 1: 输入: nums [-1,0,3,5,9,12], target 9 输出: 4…...

Day50代码随想录动态规划part12:309.最佳买卖股票时机含冷冻期、714.买卖股票的最佳时机含手续费
Day50 动态规划part12 股票问题 309.最佳买卖股票时机含冷冻期 leetcode题目链接:309. 买卖股票的最佳时机含冷冻期 - 力扣(LeetCode) 题意:给定一个整数数组,其中第 i 个元素代表了第 i 天的股票价格 。设计一个算…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...
