transformer与beter
transformer与beter
- 解码和编码器含义
- tokizer标记器和one-hot独热编码
- 编码解码--语义较好的维度空间
- 矩阵相乘--空间变换
- 编码理解
- 如何构造降维的嵌入矩阵--实现到达潜空间
- 上面是基础,下面是transformer正文
- 自注意力机制
- 注意力分数--上下文修正系数
- 为什么需要KQ两个矩阵,并且还是转置,进行相乘?
- 交叉注意力机制
- 绝对位置编码--对输入的数据进行修饰
- 相对位置编码--修饰在注意力分数上面
- 多头注意力机制
- 解码器掩码---正则残差
- 模型框架
入门1:从编解码和词嵌入开始,一步一步理解Transformer,注意力机制(Attention)的本质是卷积神经网络(CNN) - YouTube
中英文翻译大概原理就是:把中文的token和英文的token,分别投射到对应的潜空间中(embeding),之后将两个潜空间进行统一
潜空间里面每个位置代表不同的语义,如果单看位置上面的值,不能获得详细的语义。需要将所有特征(也就是不同位置的语义)合起来看,才能代表详细的语义,同理图片的特征也是一样,需要将不同通道(也就是不同特征)上面的点合起来。才能知道图片该店的具体含义

解码和编码器含义
主要是解的码:是语义也就是上下文关系

如图,相当于存在一种上下文语义密切的话,在高维空间具有更近的模长之类的关系
tokizer标记器和one-hot独热编码
实现对token(也就是单位词)做数字化
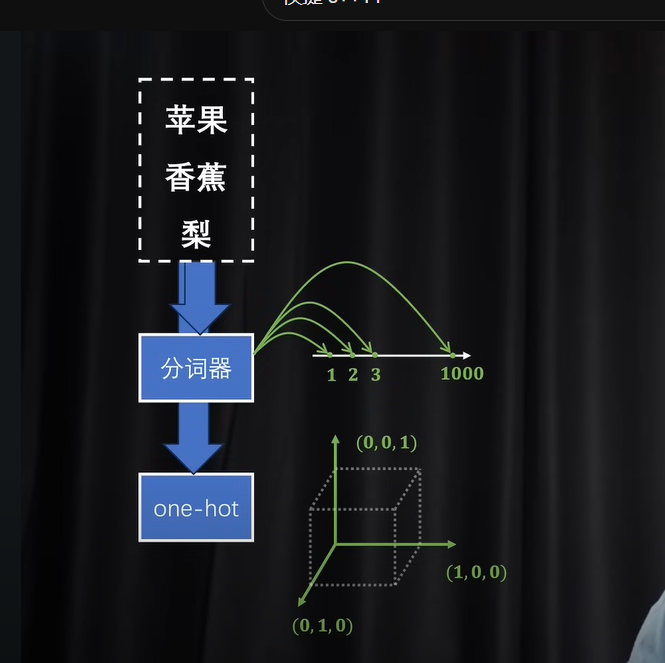
大概关系就是前者给id,后者给种类标记
但不过这种简单的表示方法不能产生语义关系,也就是
假设手机是(1)苹果是2.这样虽然很近,但其实没有具体的语义关系
前者信息过于密集无法区分语义,后者信息过于稀疏,每个token基本都占据了一个维度
编码解码–语义较好的维度空间
这样既能利用好高维度空间也能利用空间的长度
因此想法有两个:
想法一:使用分词器(tokzier)获得,密集信息,在进行升高维度
想法二:使用独热编码(one-hot)获得稀疏信息,在进行降低维度(压缩数据)
主要是运用想法二的思想
矩阵相乘–空间变换

![[images/Pasted image 20240418202413.png]]
如果只是向量和矩阵的乘法,那么只会出现向量在新的坐标系下面的旋转和伸缩,也就是空间的变换,但不过值任然是一一对应的
如果采用矩阵相乘这个二次型的方式,就会像函数一样,向量出现形状的变化
下图演示
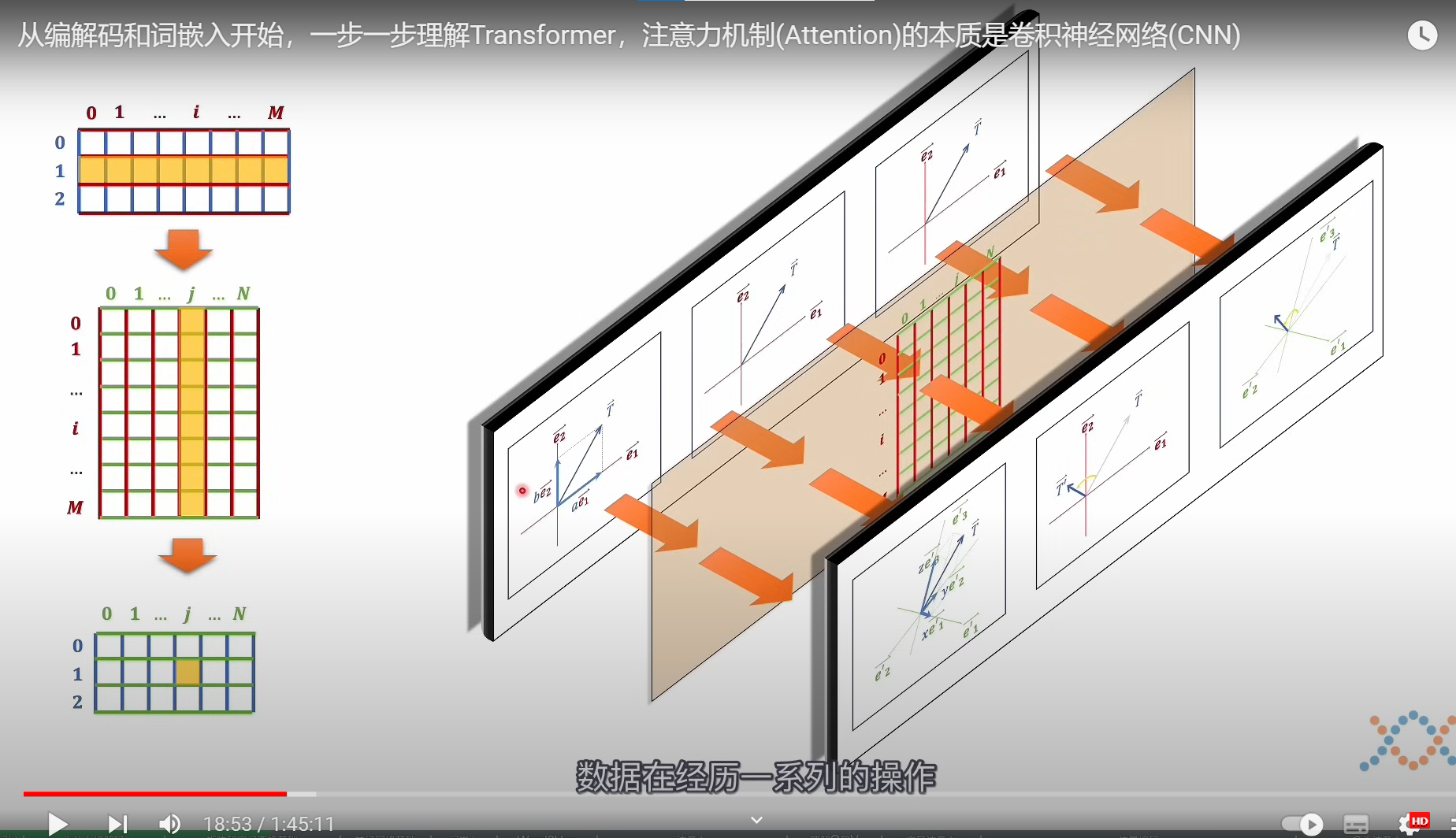
代表三个向量,也就是三个数据经过空间变换(矩阵),得到新空间的数据,所以规则(矩阵)和数据不能够进行颠倒
编码理解
先把一个文本里面的token(词元)变成独热码(获取稀疏信息),之后在进行降维(获取词元之间的语义关系(这里可以采用之前理解的距离))
总结:这个相当于把输入的一句话根据语义映射到到高维(独热编码),在把它投射到低维空间,这个也就是嵌入过程(embeding)(这个嵌入维度也就是潜空间)
相当于一个token被映射到潜空间之后,向量上面的位置,代表了不同的语义
例如

潜空间里面向量的不同值代表是该语义的程度,我们无法人为可知
如何构造降维的嵌入矩阵–实现到达潜空间
word2vec下面的:
第一个CBOW(邻字模型)

相当于用上下文的token(词元)(可能需要先升维度——独热编码),通过嵌入矩阵,获得嵌入向量,之后进行相加,将结果作为中间词元的嵌入向量,这样就可以于真实的词元向量进行比较了,进行修正
第一个跳字模型同理

最终的目的就是为了获得嵌入矩阵
转化为神经网络如下

只需要训练一个w即可,因为解码过程是一个逆过程,但实际过程好像是都要训练
不需要激活函数,因为只是对向量进行见简单的相加和分解
上面是基础,下面是transformer正文

核心是如何将得到的潜空间(embeding),去理解它的语义–注意力机制
自注意力机制
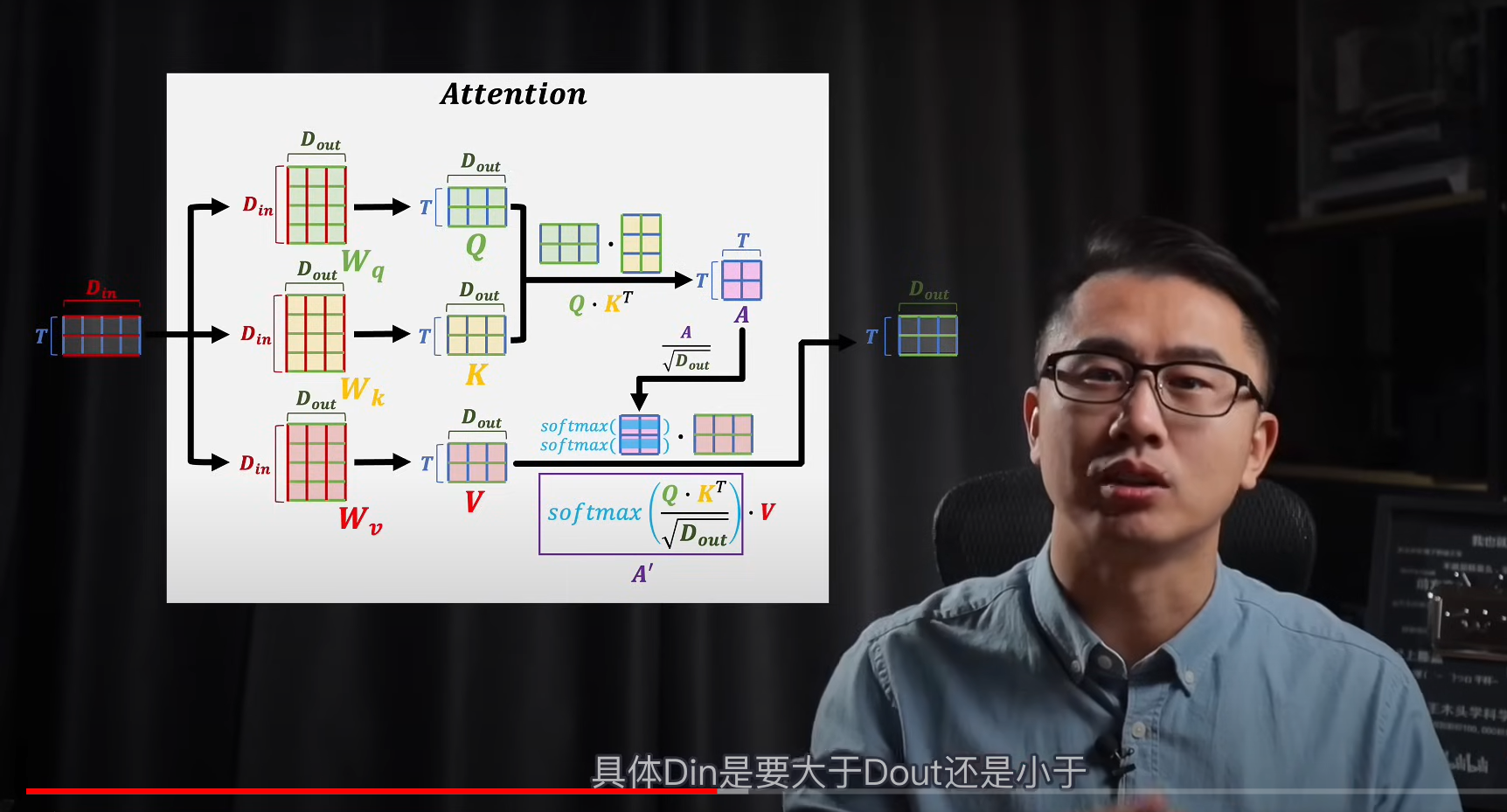
由于我们需要上下文语义的关系,输入到注意力那块的时候,不能是单个词的词嵌入向量,需要输入多个(T个,嵌入向量维度是Din)
- 按照原理,输入的词向量组,需要和三个矩阵进行空间变化得到KQV,三个状态矩阵
- 之后将K,Q其中一个转置相乘,得到T X T的矩阵,之后对改矩阵进行缩放,其实就是缩放它的方差到1上面
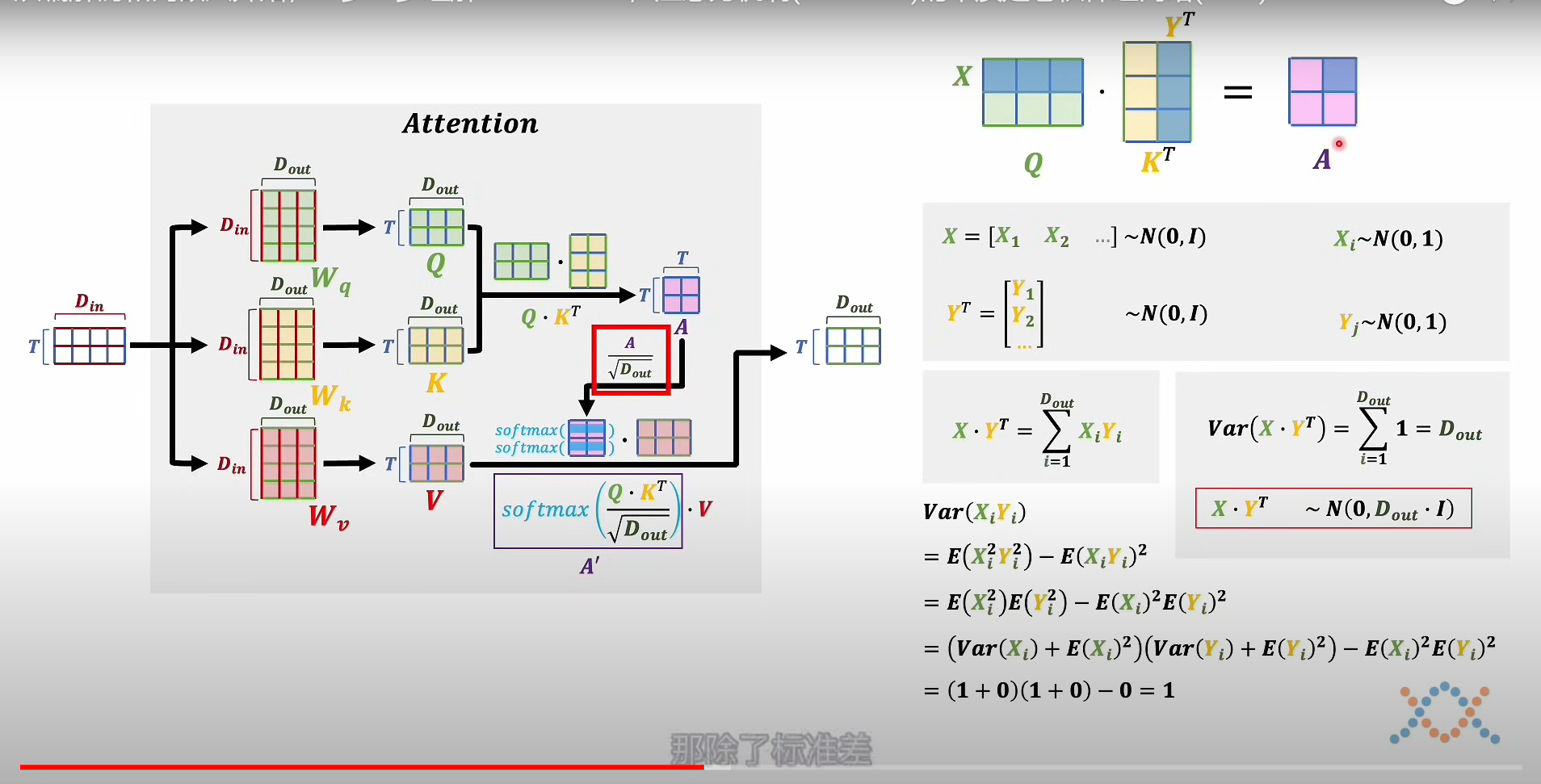
- 之后缩放的矩阵进行softmax,这里是按照行进行概率归一(这样获得了注意力分数),最后将其和V相乘,得到输出注意力结果T X Dout
总结:这个注意力分数相当于是该词在上下文关联的修改系数,而V就是该词在嵌入空间的客观语义。
注意力分数–上下文修正系数
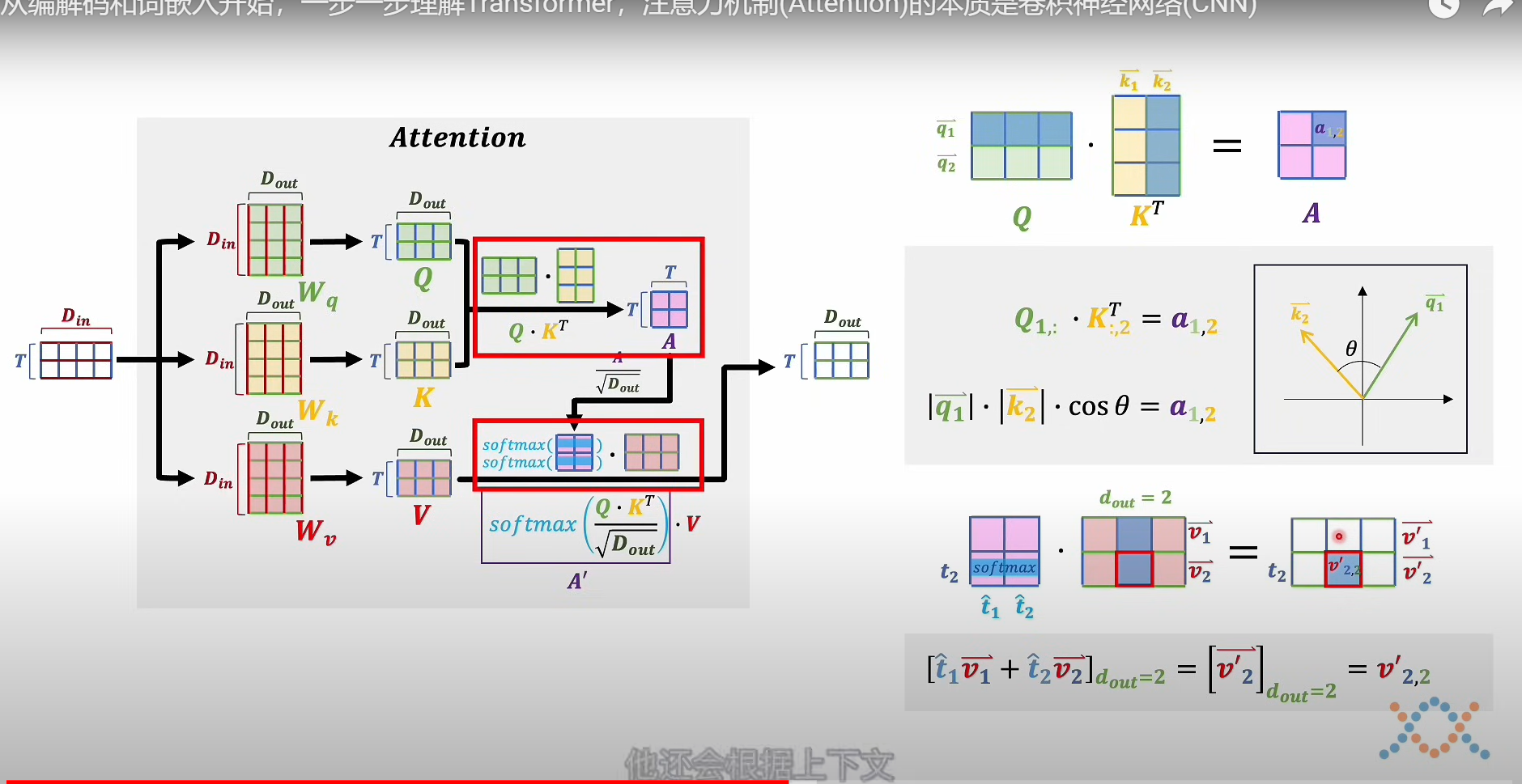
转置相乘得到的矩阵是:所有词向量之间的关联性,之后被转化为概率权重(上下文关系),最后用来修正次元的客观语义
为什么需要KQ两个矩阵,并且还是转置,进行相乘?

因为这样就构造了,二次型,能够更好的表达模型的复杂情况,更好的理解语义
需要K和Q,也是因为在上下文语义中,我们需要区分该词的设定语义和表达语义,也就是前后关系,所以猜测需要两个矩阵,KQ
交叉注意力机制

相当于拿到解码器的主观语义里面的设定语义,与解码器的KV,进行操作
其实是相当于有了一份主观语义里面设定语义的参考资料,相当于不需要理解主观语义,学起来很被动,但在机器翻译上面就没有问题
绝对位置编码–对输入的数据进行修饰
将0-n这些数字,通过傅里叶变换到相同嵌入向量的维度

不同语义(特征)之间相互正交,且不同token之间的编码也不相同
相对位置编码–修饰在注意力分数上面
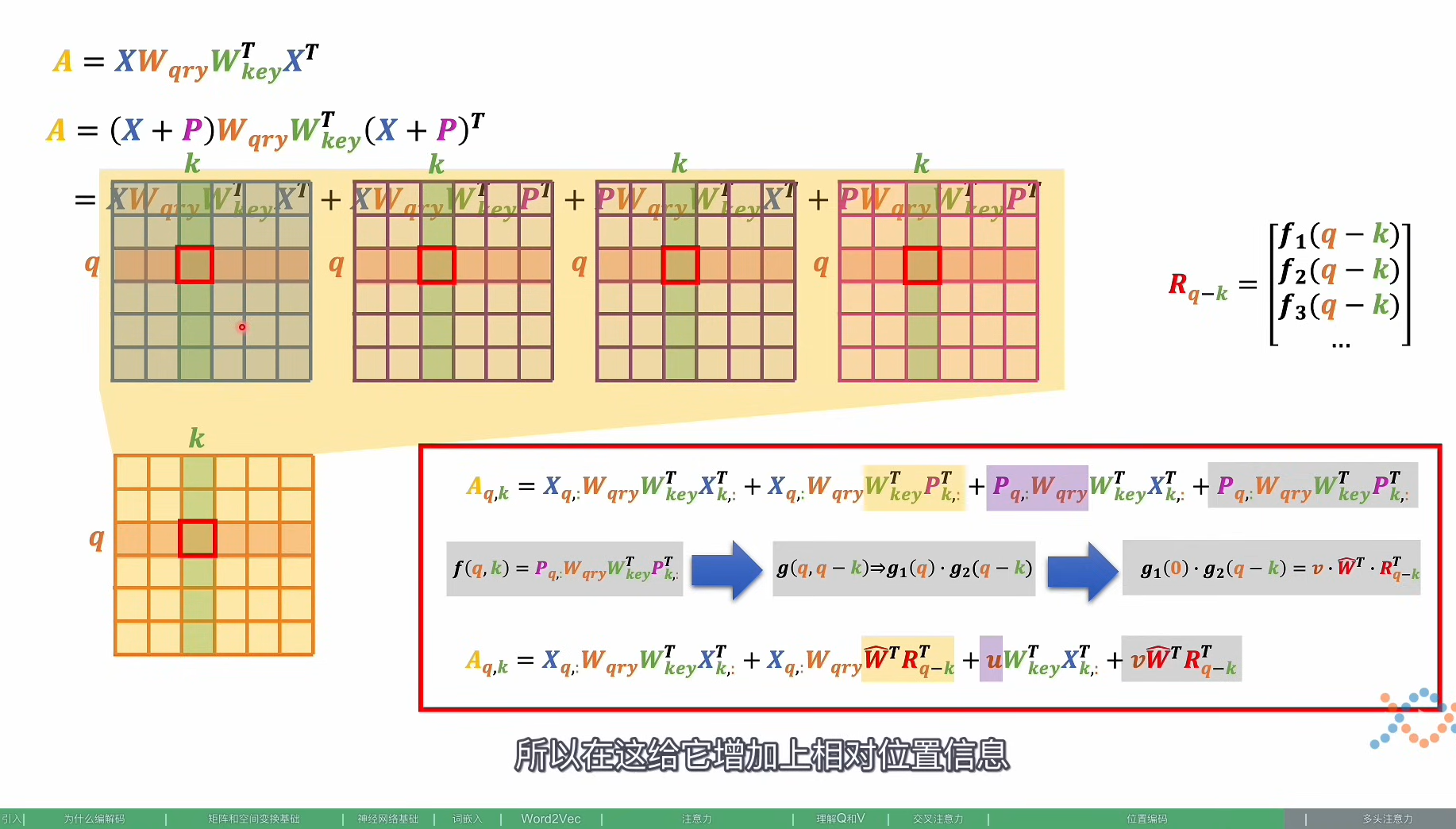
多头注意力机制

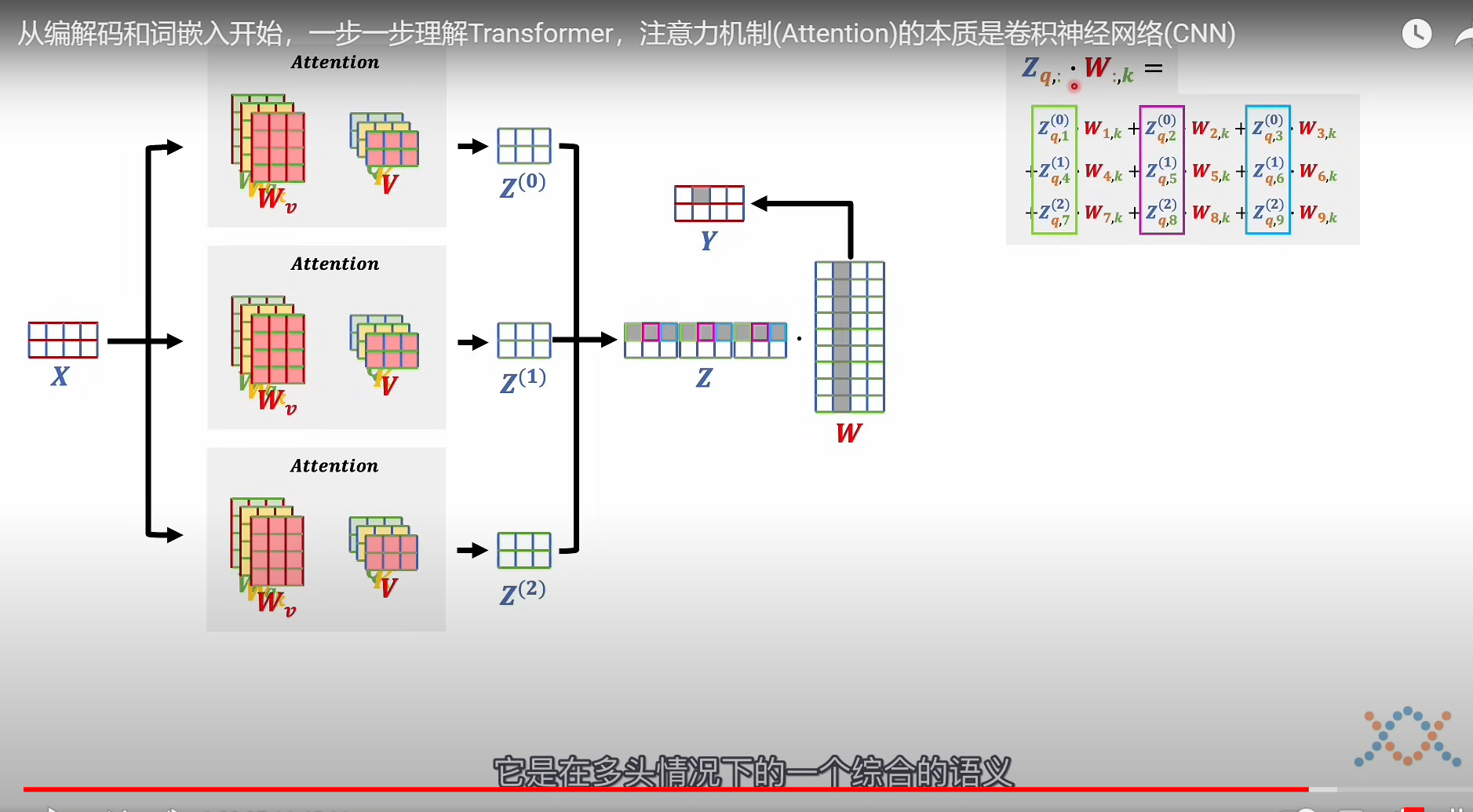
大概就是一个token(嵌入向量)进去,经过多头,一个小语义会被学习到更多相似的语义或者更大的跨度,最后通过多头相加综合起来,相当于学习到相似语义的综合语义
解码器掩码—正则残差
在推理过程需要屏蔽掉之后词语的影响

屏蔽掉一个词之后的注意力分数
正测残差
把数据加起来在正则化
残差能够学习到变化的程度
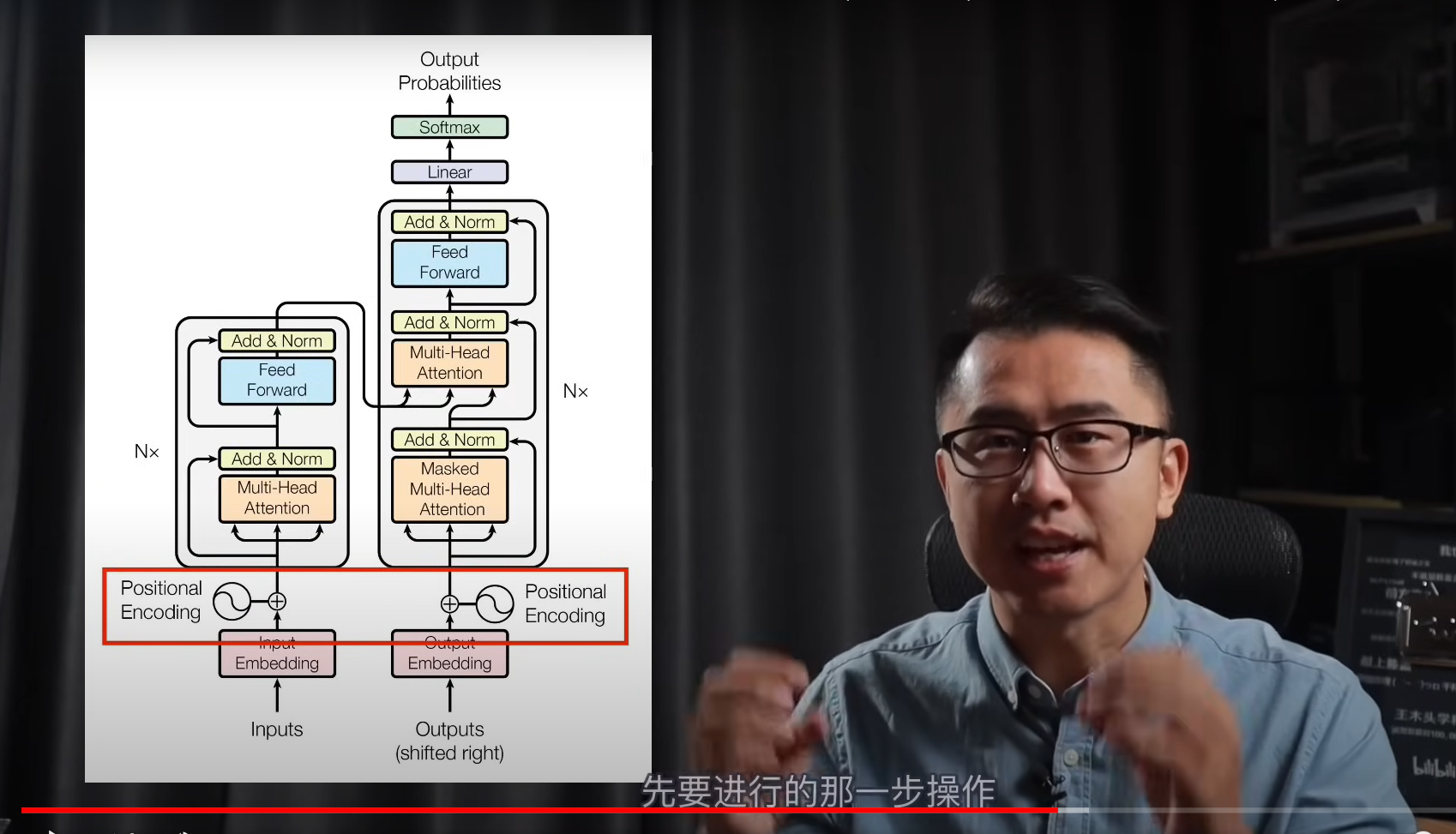
模型框架

每一个解码器的输出,都要拿着解码器的参考去更新差异
推理部分
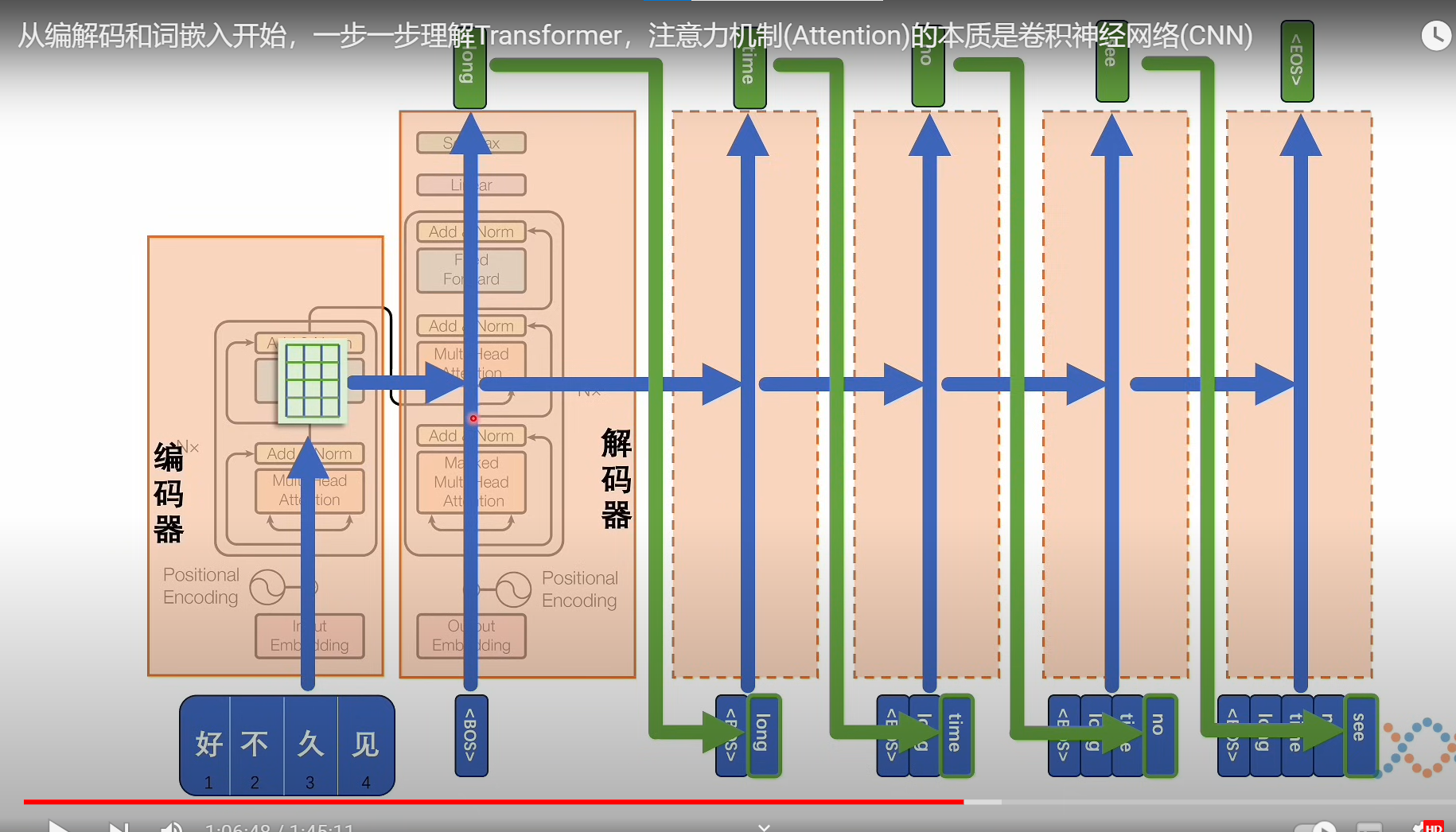
可能最后的softmax部分的输出是一个,形状确实不变都是,T X Dout,解码器部分提供的是K
相关文章:

transformer与beter
transformer与beter 解码和编码器含义tokizer标记器和one-hot独热编码编码解码--语义较好的维度空间矩阵相乘--空间变换编码理解如何构造降维的嵌入矩阵--实现到达潜空间上面是基础,下面是transformer正文自注意力机制注意力分数--上下文修正系数为什么需要KQ两个矩…...

MySQL索引设计遵循一系列原则
高频查询与大数据量表:对查询频次较高且数据量较大的表建立索引。这是因为索引主要是为了加速查询过程,对于经常需要访问的表和数据,索引的效果最为显著。 选择合适索引字段:从WHERE子句中提取最佳候选列作为索引字段,…...

windows窗口消息队列与消息过程处理函数
在Windows窗口应用程序中,消息队列和窗口过程函数是实现消息驱动机制的核心组件。 消息队列(Message Queue): 消息队列是用于存储窗口消息的缓冲区。当用户与应用程序交互时,系统会将生成的消息插入到消息队列中&…...

【Chisel】chisel中怎么处理类似verilog的可变位宽和parameter
在 Chisel 中处理可变位宽和参数的方式与 Verilog 有一些不同,因为 Chisel 是建立在 Scala 语言之上的。以下是如何在 Chisel 中处理这些概念的方法: 参数化(Parameters) 在 Chisel 中,参数化是通过在模块构造函数中定…...

[Easy] leetcode-225/232 栈和队列的相互实现
一、用栈实现队列 1、题目 仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty): 实现 MyQueue 类:void push(int x) 将元素 x 推到队列的末尾 int pop() 从队列的开头移除并返回元素 …...
Springboot+Vue项目-基于Java+MySQL的个人云盘管理系统(附源码+演示视频+LW)
大家好!我是程序猿老A,感谢您阅读本文,欢迎一键三连哦。 💞当前专栏:Java毕业设计 精彩专栏推荐👇🏻👇🏻👇🏻 🎀 Python毕业设计 &…...

Leetcode 116:填充每一个节点的下一个右侧节点指针
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下: struct Node {int val;Node *left;Node *right;Node *next; } 填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到…...
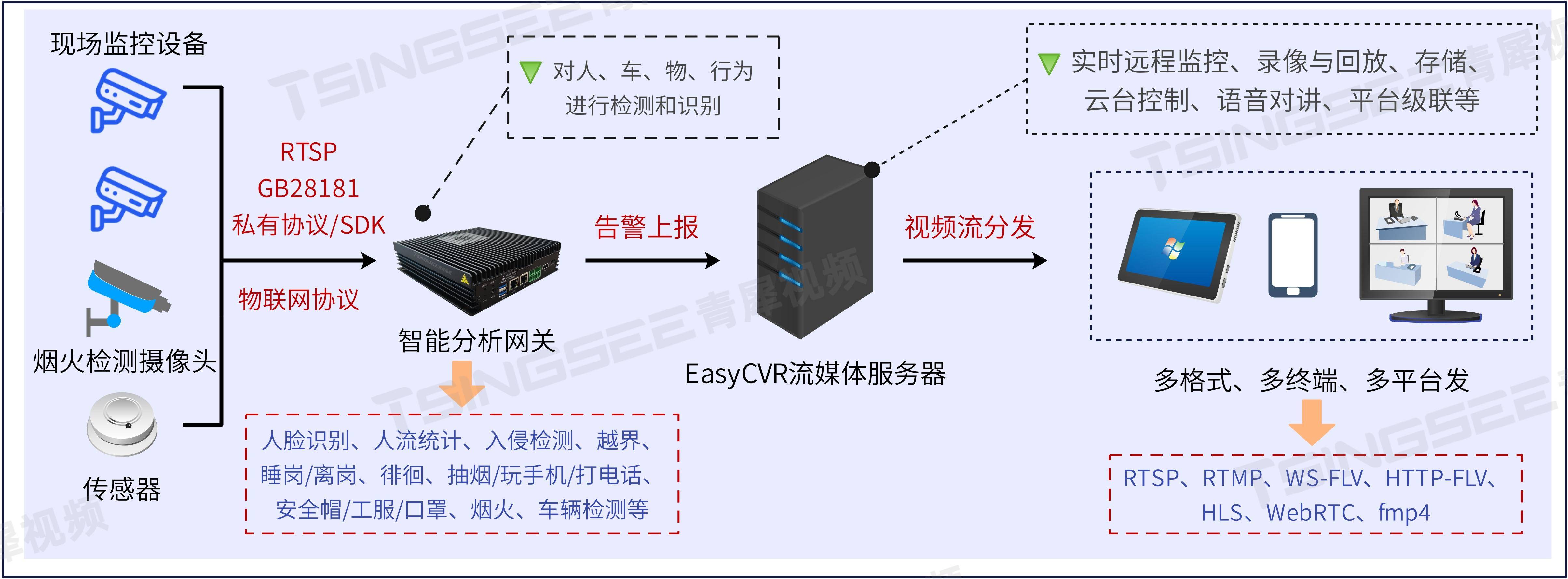
AI智能分析赋能EasyCVR视频汇聚平台,为安全生产监管提供保障
一、背景需求 为提升公共及生产安全监管,深入贯彻落实中央关于智慧城市、数字乡村的部署要求,视频设备融合管理已成为视频治理的必然趋势。针对当前部分地区在视频监控系统建设中存在的问题,如重点地区视频监控系统建设零散、视频监控数据孤…...

Java设计模式 _结构型模式_外观模式
一、外观模式 1、外观模式 外观模式(Facade Pattern)是一种结构型模式。主要特点为隐藏系统的复杂性,并向客户端提供了一个客户端可以访问系统的接口。这有助于降低系统的复杂性,提高可维护性。当客户端与多个子系统之间存在大量…...

数据结构之----栈与队列
栈是限定仅在表尾进行插入和删除操作的线性表; 队列是只允许在一端进行插入操作,而另一端进行删除操作的线性表; 栈,允许插入和删除的一端称为栈顶,另一端称为栈底,特点后进先出。 插入操作称为进栈&#…...
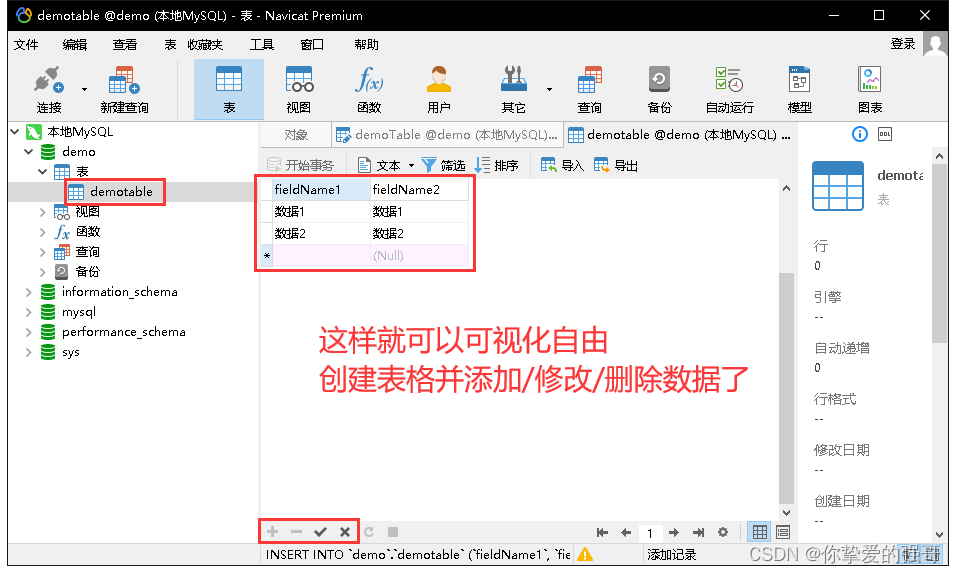
如何在windows server下安装mysql5.7数据库,并使用Navicat Premium 15可视化工具新建数据库并读取数据库信息。
如何在windows server下安装mysql5.7数据库? MySQL :: Download MySQL Community Server (Archived Versions)https://downloads.mysql.com/archives/community/点击↑,然后选择对应版本和平台↓下载 将下载后的安装包放入固定目录(这里以D:…...

Calendar 366 II for Mac v2.15.5激活版:智能日历管理软件
在繁忙的工作和生活中,如何高效管理日程成为了许多人的难题。Calendar 366 II for Mac,作为一款全方位的日历管理软件,以其独特的功能和优秀的用户体验,成为您的日程好帮手。 Calendar 366 II for Mac支持多种视图模式,…...
react引入阿里矢量库图标
react引入阿里矢量库图标 登录阿里矢量库,将项目所需的图标放一起 react项目中新建文件夹MyIcon.js 3. 在页面中引入,其中type为图标名称...
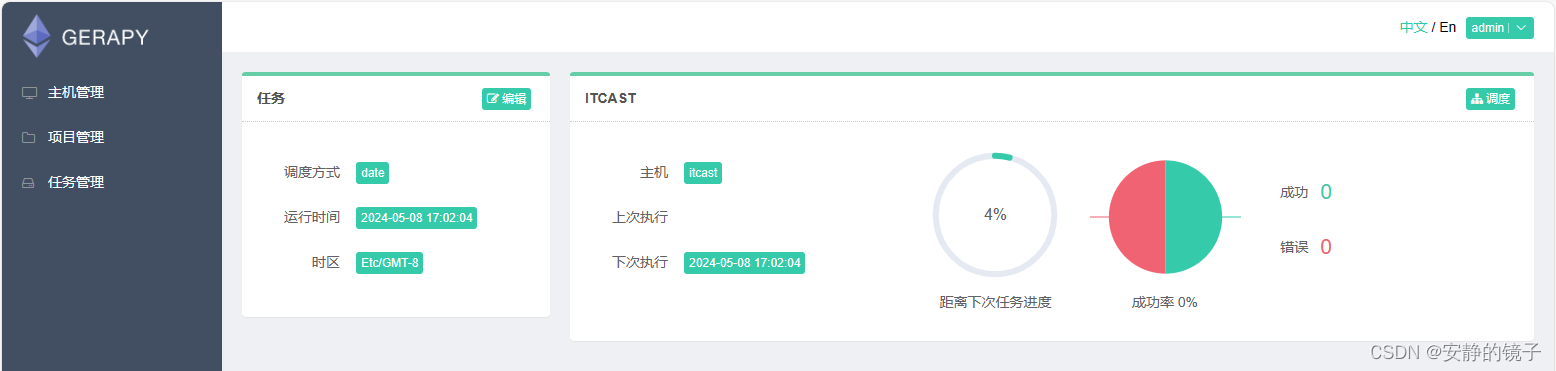
部署Gerapy
1.Gerapy 是什么? Gerapy 是一款基于 Python 3 的分布式爬虫管理框架,它旨在简化和优化分布式爬虫的部署、管理和监控过程。 2.作用与功能? 2.1分布式管理: Gerapy 允许用户在多台机器上部署和管理Scrapy爬虫,实现爬虫…...

Github Benefits 学生认证/学生包 新版申请指南
本教程适用于2024年之后的Github学生认证申请,因为现在的认证流程改变了很多,所以重新进行了总结这方面的指南。 目录 验证教育邮箱修改个人资料制作认证文件图片转换Base64提交验证 验证教育邮箱 进入Email settings,找到Add email address…...

基于单片机的宠物智能投喂系统研究
目录 第一章 研究背景和意义.................................................................... 4 1.1 研究背景....................................................................................... 5 1.2 研究目的.............................................…...

Linux-笔记 常用命令
(持续更新) 1、压缩: tar -vcjf test1.tar.bz2 test1 tar -vczf test1.tar.gz test1 2、解压 tar -vxjf test1.tar.bz2 tar -vxzf test2.tar.gz 3、查找 find [路径] [参数] [文件名] : find / -name test* grep [参数] 关键字 路径&a…...

MySQL中,关于日期类型的那些事儿,你知道哪些?
在MySQL数据库中,除了前面我们聊到的数字类型和字符串类型,还有一个常用的数据类型:日期类型。在我们业务表中,基本上每个业务表都有日期类型,用于记录创建时间和修改时间。比如我们的用户表,一般除了要记录…...
【Chrome实用命令笔记】
文章目录 Chrome实用命令笔记1、chrome基本介绍2. 打开开发者工具(DevTools)方法一:快捷键方法二:右键菜单方法三:浏览器设置 2. 开发者工具面板Elements面板Console面板Sources面板Network面板Performance面板Memory面…...

【数据库】数据库事务原理
事务特性 https://blog.csdn.net/zxcyxg123/article/details/132020499 MVCC MVCC(Multi-Version Concurrency Control),即多版本并发控制,是一种并发控制的方法,主要用于数据库管理系统中,以实现对数据库…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...
