C++笔试强训day20
目录
1.经此一役小红所向无敌
2.连续子数组最大和
3.非对称之美
1.经此一役小红所向无敌
链接
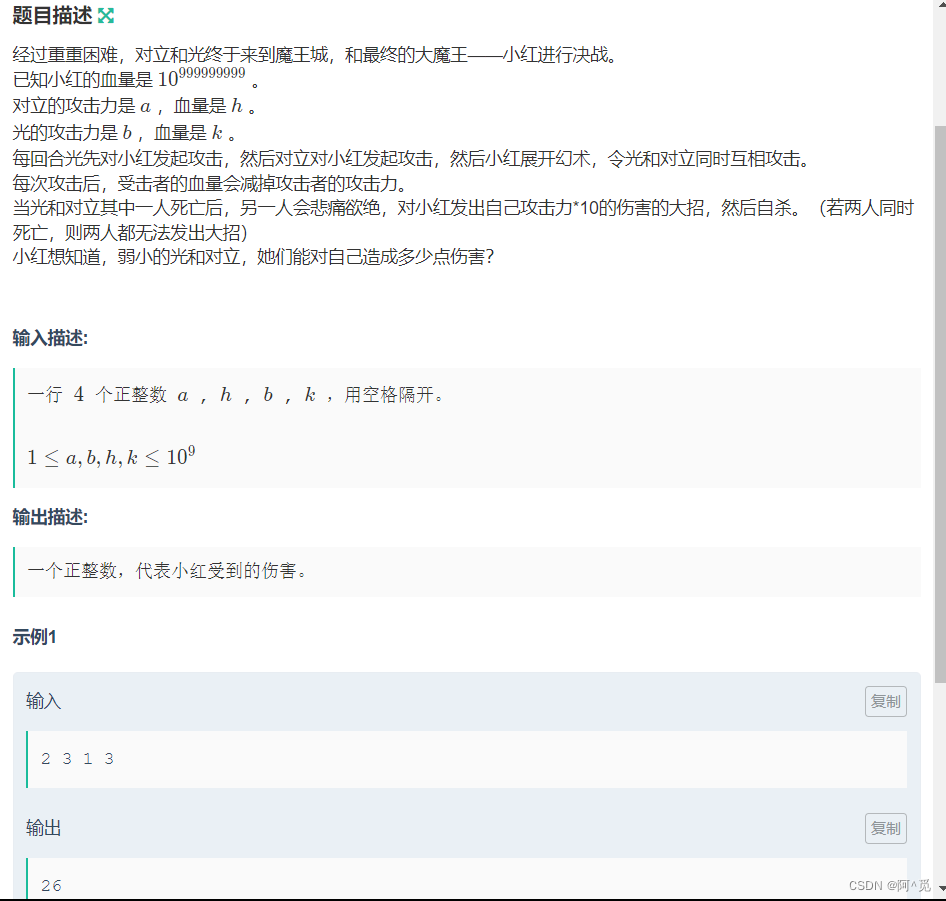
简单模拟即可。
需要注意的是:
除完之后有无余数,若有,则还可以再挨一次打。

#include <iostream>
using namespace std;
#define int long long
int a, h, b, k;
signed main() {cin >> a >> h >> b >> k;int sum = 0;int cnt1 = h / b;int cnt2 = k / a;if (h % b != 0)cnt1++;if (k % a != 0)cnt2++;int cnt = min(cnt1, cnt2);sum += cnt * (a + b);if (cnt1 == cnt2)cout << sum << endl;else if (cnt1 > cnt2){sum += a * 10;cout << sum << endl;}else if (cnt1 < cnt2){sum += b * 10;cout << sum << endl;}return 0;
}2.连续子数组最大和
链接

一道线性dp问题,最主要的是找出dp所表示的含义:
dp[i], 以i为结尾,可以表示的最大数值。
#include <iostream>
using namespace std;const int N = 2e5 + 10;
int dp[N];
int v[N];
int main() {int n;cin >> n;for(int i = 1; i <= n; ++i)cin >> v[i]; for(int i = 1; i <= n; ++i)dp[i] = max(dp[i - 1] + v[i], v[i]);int ret = -101;for(int i = 1; i <= n; ++i)ret = max(dp[i], ret);cout << ret << endl;return 0;
}填完表后,遍历一遍表中的数,取出最大值即可。
由于![]() ,因此可以让 ret 初始化为 -101。
,因此可以让 ret 初始化为 -101。
3.非对称之美
链接

我认为这就是一道数学分析找规律题,暴力强解复杂度太高,易超时,解不出来。
但是这个规律也不好找:
#include <iostream>
#include <string>
using namespace std;
int n;
string s;
int fun()
{// 1. 判断是否全都是相同字符bool flag = false;for (int i = 1; i < n; i++){if (s[i] != s[0]){flag = true;break;}}if (flag == false) return 0;// 2. 判断本⾝是否是回⽂flag = true;int left = 0, right = n - 1;while (left < right){if (s[left] == s[right]){left++;right--;}else{flag = false;break;}}if (flag) return n - 1;else return n;
}
int main()
{cin >> s;n = s.size();cout << fun() << endl;return 0;
}若字符全相同,则返回0。
若从0和n - 1往中间遍历,存在不相同,即可直接break返回 n (个数)。
若全相同,则返回 n - 1。
即这时个对称数,但是如果你取除第一个或最后一个外的所有字符,即可组成非对称。
题目有要求要最大,所以为 n - 1。
相关文章:
C++笔试强训day20
目录 1.经此一役小红所向无敌 2.连续子数组最大和 3.非对称之美 1.经此一役小红所向无敌 链接 简单模拟即可。 需要注意的是: 除完之后有无余数,若有,则还可以再挨一次打。 #include <iostream> using namespace std; #define in…...

【PHP【实战项目】系统性教学】——使用最精简的代码完成用户的登录与退出
👨💻个人主页:开发者-曼亿点 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 曼亿点 原创 👨💻 收录于专栏:…...
Linux下的常用基本指令
基本指令 前言一、ls 指令语法功能常用选项举例注意要点关于拼接关于 -a关于文件ls与/的联用ls与根目录ls与任意文件夹ls与常用选项与路径 ls -d与ls -ldls与ll 二、pwd命令语法功能常用选项注意要点window与Linux文件路径的区别家目录 三、cd 指令语法功能举例注意要点cd路径.…...

phpstorm环境配置与应用
在 PhpStorm 中配置 PHP 开发环境及进行一些常用的应用设置涉及以下几个主要步骤: ### 1. 安装和激活 PhpStorm - **下载安装**: 访问 JetBrains 官网下载最新版本的 PhpStorm 安装包,然后按照提示进行安装。 - **激活**: 启动 PhpStorm,你可…...

【Qt 学习笔记】Qt常用控件 | 布局管理器 | 水平布局Horizontal Layout
博客主页:Duck Bro 博客主页系列专栏:Qt 专栏关注博主,后期持续更新系列文章如果有错误感谢请大家批评指出,及时修改感谢大家点赞👍收藏⭐评论✍ Qt常用控件 | 布局管理器 | 水平布局Horizontal Layout 文章编号&…...
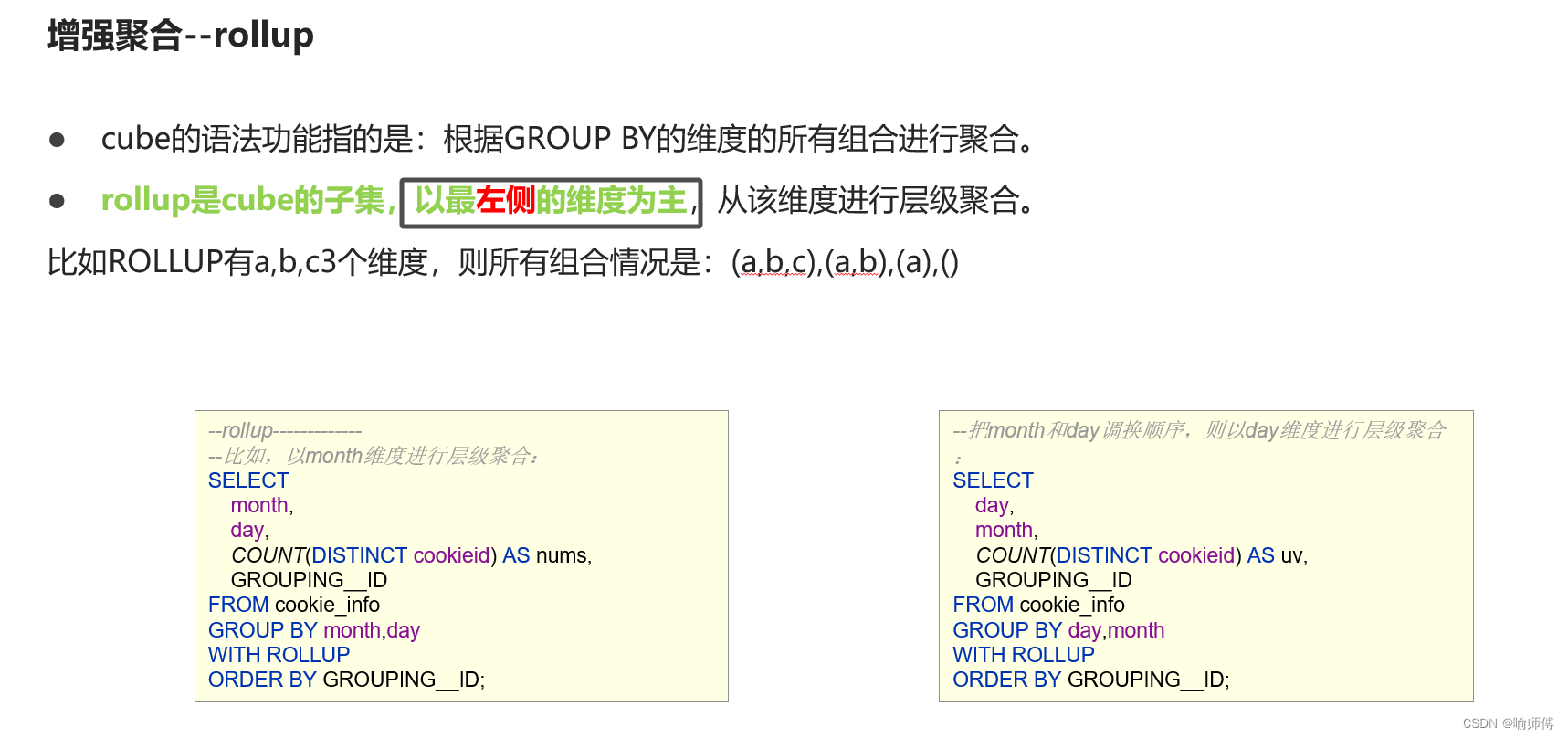
Hive Aggregation 聚合函数
Hive Aggregation 聚合函数 基础聚合 增强聚合...
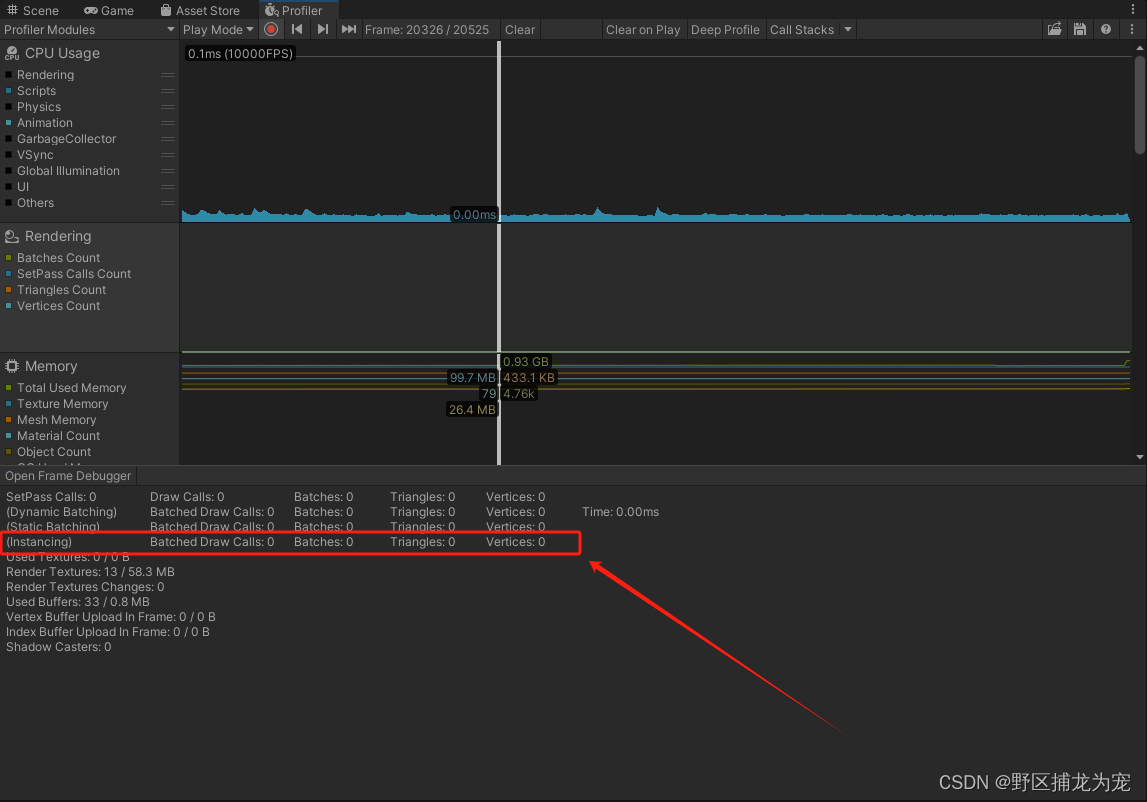
Unity 性能优化之GPU Instancing(五)
提示:仅供参考,有误之处,麻烦大佬指出,不胜感激! 文章目录 前言一、GPU Instancing使用方法二、使用GPU Instancing的条件三、GPU Instancing弊端四、注意五、检查是否成功总结 前言 GPU Instancing也是一种Draw call…...
LeetCode 138. 随机链表的复制
目录 1.原题链接: 2.结点拆分: 代码实现: 3.提交结果: 4.读书分享: 1.原题链接: 138. 随机链表的复制 2.结点拆分: ①.拷贝各个结点,连接在原结点后面; ②.处…...

【PC微信小程序点不动处理方法】
描述 在使用电脑小程序抓包的时候发现原来能点的小程序今天不能点了。就是原来有个输入车牌号的输入框点击会出现车牌号键盘,现在不行了,经过卸载安装发现不是微信的问题,是WeChatAppEx.exe 的bug。早期使用的是不带ex的都没有问题升级以后&…...

量化交易:日内网格交易策略.md
哈喽,大家好,我是木头左! 本文将详细介绍日内网格交易策略的原理,并结合Python代码示例,展示如何在掘金平台上实现这一策略。 策略原理 日内网格交易策略的核心思想是在一天的交易时间内,通过设置多个买卖…...
Ubuntu 20.04在Anaconda虚拟环境中配置PyQt4
一、创建一个虚拟环境 1 创建一个python2.7的虚拟环境: conda create -n pyqt4 numpy matplotlib python2.72 在环境中安装几个需要的包: pip install Theano pip install python-opencv3.4.0.14 pip install qdarkstyle pip install dominate二、在主…...

charts3D地球--添加航线
要在地球视角下画出海运路线图 方案 添加 globl 地球创建geo地理坐标系创建canvas对象用于承载地图世界地图this.worldChart //初始化canvas节点let cav document.createElement("canvas");this.$echarts.registerMap("world", geoJson);this.worldCha…...

变色龙还是树懒:揭示大型语言模型在知识冲突中的行为
你是知识变色龙还是树懒?我今天在ICLR学到一个很有趣的术语,叫做证据顺序(order of evidence)。 大模型RAG处理知识冲突的探讨: 在检索增强生成(Retrieval-Augmented Generation, RAG)的过程中,技术团队会将检索到的前几名文档作为证据,并提示(prompt)给大型语言模型(Large La…...
OMX Core)
Android OpenMAX(四)OMX Core
假设我们已经写好了所有的OMX组件,有vdec、venc、adec、aenc,接下来问题来了,我们应该如何管理这些组件呢(创建、销毁)?这一篇文章我们向上一层学习OMX Core提供的标准API。 OMX Core代码位于 OMX_Core.h OMX Core在OpenMAX IL架构中的位置位于IL Client与实际的OMX组件之…...

【Linux】轻量级应用服务器如何开放端口 -- 详解
一、测试端口是否开放 1、测试程序 TCP demo 程序(可参考:【Linux 网络】网络编程套接字 -- 详解-CSDN博客) 2、测试工具 Windows - cmd 窗口 输入命令:telnet [云服务器的公网ip] [port] 二、腾讯云安全组开放端口 1、安全组设…...

git如何查看密码
git查看用户名、邮箱 git config user.name git config user.email 也可以在系统,用户文件夹下面 gitconfig查看 通常无法查看git密码,运行以下命令 git config credential.helper 查看储存的方式,如果是manage 或manage-store则说明是…...

redis脑裂问题
1. 前言 脑裂就是指在主从集群中,同时有两个主节点,它们都能接收写请求。而脑裂最直接的影响,就是客户端不知道应该往哪个主节点写入数据,结果就是不同的客户端会往不同的主节点上写入数据。而且,严重的话,…...

日本率先研发成功6G设备,刺痛了谁?为何日本能率先突破?
日本率先研发成功6G设备,无线数据速率是5G的百倍,这让日本方面兴奋莫名,毕竟日本在科技方面从1990年代以来太缺少突破的创新了,那么日本为何如今在6G技术上能率先突破呢? 日本在1980年代末期达到顶峰,它的科…...
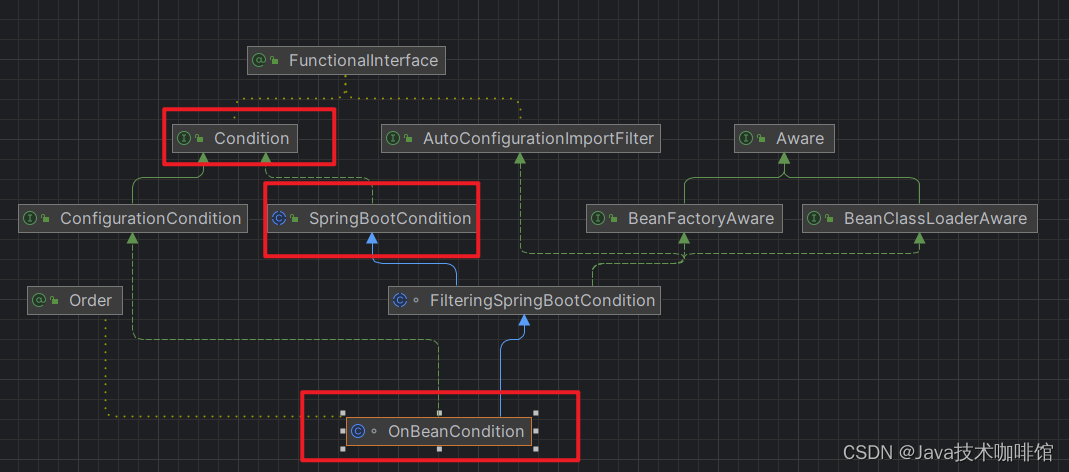
SpringBoot自动配置源码解析+自定义Spring Boot Starter
SpringBootApplication Spring Boot应用标注 SpringBootApplication 注解的类说明该类是Spring Boot 的主配置类,需要运行该类的main方法进行启动 Spring Boot 应用 SpringBootConfiguration 该注解标注表示标注的类是个配置类 EnableAutoConfiguration 直译&#…...

Kafka 环境配置与使用总结
# 部署教程参考 # 官方教程: https://kafka.apache.org/quickstart # 单机部署kafka参考: https://blog.csdn.net/u013416034/article/details/123875299 # 集群部署kafka参考: # https://blog.csdn.net/zhangzjx/article/details/123679453 # https://www.cnblogs.com/And…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...
