机器学习(五) ----------决策树算法
目录
1 核心思想
2 决策树算法主要步骤
3 决策树算法的分类
3.1 ID3算法(Iterative Dichotomiser 3):
3.1.1 基本步骤
3.1.2 原理
信息增益
3.1.3 注意事项
3.2 C4.5算法:
3.2.1. 信息增益率
计算公式
3.2.2. 构建决策树
3.2.3 优点
3.2.4 缺点
3.3 CART(Classification and Regression Trees)算法
3.3.1分类树构建
3.3.2 回归树构建
3.3.3 CART算法的优点
3.3.4 CART算法缺点
4 决策树的剪枝
4.1 预剪枝(Pre-pruning)
4.1.1 优点
4.1.2 缺点
4.2 后剪枝
4.2.1 优点
4.2.2 缺点
4.3 剪枝相关API
5 决策树API
5.1 分类决策树
sklearn.tree.DecisionTreeClassifier
5.2 回归决策树
sklearn.tree.DecisionTreeRegressor
6 代码实现
1 核心思想
决策树算法(Decision Tree)是一种常用的监督学习算法,用于分类和回归任务。核心思想是将整个数据集按照某种属性进行划分,形成类似于树的结构,每个内部节点表示一个属性上的测试,每个分支代表一个测试输出,每个叶节点代表一种类别。
2 决策树算法主要步骤
- 特征选择:选择对数据集划分能力最好的特征,即能够最大化信息增益、增益率、基尼指数等的特征。
- 决策树生成:根据选择的特征对数据集进行划分,生成决策树。
- 决策树剪枝:为了避免过拟合,需要对生成的决策树进行剪枝,去掉一些分支以降低模型的复杂度。
3 决策树算法的分类
3.1 ID3算法(Iterative Dichotomiser 3)
ID3算法(Iterative Dichotomiser 3)是一种决策树学习算法,由Ross Quinlan在1986年提出。该算法的核心思想是使用信息增益(Information Gain)作为选择划分属性的度量标准,从而构建一棵决策树来分类实例。
3.1.1 基本步骤
-
准备数据集:数据集需要是离散的,并且包含特征和类别标签。
-
计算信息增益:对于数据集中的每个非类别特征(属性),计算其作为划分属性的信息增益。
-
选择最佳划分属性:选择信息增益最大的特征作为当前节点的划分属性。
-
划分数据集:根据选择的最佳划分属性,将数据集划分为若干个子集,每个子集对应该属性的一个可能取值。
-
递归构建决策树:对每个划分后的子集,重复步骤2至4,直到满足停止条件(如子集的所有实例都属于同一类别,或者没有特征可供划分)。
-
形成决策树:将递归过程中生成的节点和分支连接起来,形成一棵决策树。
3.1.2 原理
信息增益
信息增益是衡量一个特征划分数据集能力的指标。假设数据集D有m个类别,第i个类别有个样本,那么数据集D的信息熵(Entropy)定义为:
其中,() 是第i个类别在数据集D中出现的概率。
假设特征A有n个不同的取值(),使用特征A对数据集D进行划分,可以得到n个子集(
)。使用特征A划分数据集D后的信息熵为:
那么,特征A的信息增益为:
信息增益越大,表示使用特征A划分数据集D后,数据集的纯度提升越大,因此应该选择信息增益最大的特征作为划分属性。
3.1.3 注意事项
- ID3算法只能处理离散型数据,对于连续型数据需要进行离散化处理。
- ID3算法倾向于选择取值较多的特征进行划分,这可能会导致决策树过于复杂,出现过拟合现象。
- ID3算法没有考虑剪枝策略,生成的决策树可能不够简洁。在实际应用中,可以通过后剪枝等方法来简化决策树。
3.1.4 优点
- 易于理解和解释:ID3算法构建的决策树直观易懂,易于被非专业人士理解和解释。这种可视化的方式有助于人们更好地理解数据,从而做出更明智的决策。
- 处理离散型数据效果好:ID3算法特别适用于处理离散型数据,如文本分类、垃圾邮件过滤等场景。在这些场景中,ID3算法能够有效地根据数据的特征进行划分,从而得到准确的分类结果。
3.1.5 缺点:
- 不能处理连续型数据:ID3算法只能处理离散型数据,对于连续型数据需要进行离散化处理。这可能会导致信息丢失或处理成本增加。
- 对噪声和缺失值敏感:ID3算法对噪声和缺失值比较敏感,如果数据中存在较多的噪声或缺失值,可能会导致构建的决策树不够准确。
- 倾向于选择取值较多的属性:ID3算法在选择划分属性时,倾向于选择取值较多的属性。这可能会导致决策树过于复杂,出现过拟合现象。同时,由于信息增益的计算方式,取值较多的属性可能会被过分强调,而忽略了其他更重要的属性。
- 不能处理增量数据:ID3算法不能增量地接受训练集,每增加一次实例就需要重新构造整个决策树。这可能会导致算法在处理大规模数据集时效率较低。
3.2 C4.5算法
C4.5算法是一种经典的决策树学习算法,由Ross Quinlan在ID3算法的基础上进行改进和扩展。其核心原理是基于信息论的概念,通过计算每个属性的信息增益率(而不是ID3算法中的信息增益),来选择最佳划分属性,并以此构建决策树。
3.2.1. 基本步骤
C4.5算法通过递归地选择最佳划分属性来构建决策树。具体步骤如下:
1 选择最佳划分属性
- 对于当前数据集,计算每个属性的信息增益率。
- 选择信息增益率最大的属性作为最佳划分属性。
2 划分数据集
- 根据选定的最佳划分属性,将数据集划分为若干个子集,每个子集对应该属性的一个可能取值。
3 递归构建子树
- 对每个划分后的子集,重复步骤2.1和2.2,直到满足停止条件为止。停止条件通常包括:
- 子集中的所有实例都属于同一类别。
- 没有属性可供划分(即所有属性都已用作划分属性)。
- 子集的大小小于预定的阈值。
4 剪枝
- 为了防止过拟合,C4.5算法在构建决策树的过程中会进行剪枝。剪枝策略可以基于后验概率、交叉验证等方法。
3.2.2 原理
信息增益率
在C4.5算法中,信息增益率被用作选择最佳划分属性的标准。信息增益率考虑了属性值的数量和不同取值对分类效果的影响,从而避免了ID3算法倾向于选择取值较多的属性的问题。
计算公式
信息增益率的计算公式如下:
其中,Gain(A) 是属性A的信息增益,SplitInfo(A) 是属性A的分裂信息(Split Information)。
信息增益(Gain):表示按照属性A划分数据集前后,信息熵的减少量。它衡量了属性A对于分类任务的重要性。
分裂信息(SplitInfo):表示根据属性A的不同取值对数据集进行划分时所需的信息熵。它用于衡量属性A的取值数量对分类效果的影响。
- A 是当前考虑的属性。
- v 是属性A的不同取值的数量。
- D 是当前要划分的样本集。
- Di 是根据属性A的第i个取值划分出来的样本子集。
- ∣D∣ 和 ∣Di∣ 分别表示样本集D和子集Di的样本数量。
3.2.3 优点
- C4.5算法能够处理连续型属性或离散型属性的数据。
- C4.5算法能够处理具有缺失值的属性数据。
- C4.5算法使用信息增益率作为选择最佳划分属性的标准,优化了ID3算法倾向于选择取值较多属性的问题。
- C4.5算法生成的决策树具有较好的泛化能力。
3.2.4 缺点
- C4.5算法在构建决策树时,需要计算每个属性的信息增益率,这可能导致计算量较大。
- C4.5算法在处理大规模数据集时,可能受到内存限制的影响。
- C4.5算法生成的决策树可能不够简洁,需要进一步进行剪枝和优化。
3.3 CART(Classification and Regression Trees)算法
CART(Classification and Regression Trees)算法原理主要包括分类树的构建和回归树的构建。
3.3.1分类树构建
CART分类树算法使用基尼系数(Gini Index)作为选择最优特征的标准。基尼系数代表了模型的不纯度,基尼系数越小,不纯度越低,特征越好。CART算法通过递归地将数据集划分为两个子集来构建决策树。
1.计算基尼系数:对于给定的样本集合D,其基尼系数为
其中,K是类别的数量,是样本属于第k个类别的概率。
2.选择最优特征:对于数据集中的每个非类别特征(属性),计算其作为划分属性的基尼系数。选择基尼系数最小的特征作为当前节点的划分属性。
3.划分数据集:根据选定的最优特征及其阈值,将数据集划分为两个子集,并递归地在每个子集上重复步骤2和3,直到满足停止条件(如子集的所有实例都属于同一类别,或者没有特征可供划分)。
4.构建决策树:将递归过程中生成的节点和分支连接起来,形成一棵决策树。
3.3.2 回归树构建
当CART用作回归树时,其目标是通过递归地将数据集划分为两个子集来最小化平方误差。
-
选择最优特征:对于数据集中的每个特征,计算其作为划分属性的平方误差之和。选择平方误差之和最小的特征作为当前节点的划分属性。
-
划分数据集:根据选定的最优特征及其阈值,将数据集划分为两个子集,并递归地在每个子集上重复步骤1和2,直到满足停止条件(如子集的平方误差之和小于预定的阈值,或者没有特征可供划分)。
-
构建决策树:将递归过程中生成的节点和分支连接起来,形成一棵回归树。
在CART算法中,生成的决策树通常是二叉树,即每个节点最多有两个子节点。此外,CART算法还包括剪枝策略,以避免过拟合现象。剪枝策略可以在决策树构建过程中进行(预剪枝),也可以在决策树构建完成后进行(后剪枝)。
3.3.3 CART算法的优点
- 计算简单,易于理解,可解释性强。
- 比较适合处理有缺失属性的样本。
- 不仅能够处理不相关的特征,还能在相对短的时间内对大型数据源得出可行且效果良好的结果。
3.3.4 CART算法缺点
- 不支持在线学习,即当有新的样本产生后,决策树模型需要重建。
- 容易出现过拟合的现象,即生成的决策树可能对训练数据有很好的分类能力,但对未知的测试数据却未必有很好的分类能力。
4 决策树的剪枝
决策树的剪枝是避免过拟合现象、提升模型泛化效果的重要手段。剪枝的基本思想是将决策树的某些内部节点或子树剪掉,使得决策树变得更加简单,从而降低过拟合的风险。
4.1 预剪枝(Pre-pruning)
在决策树构建过程中进行剪枝,通过设定一些规则,提前停止树的生长。例如,可以设定决策树的深度、当前节点的样本数量阈值、信息增益或信息增益率阈值、测试集准确性提升阈值等。当达到这些阈值时,就停止对当前节点的划分,并将其标记为叶节点。预剪枝方法能有效提升模型性能,并减少训练时间和测试时间,但采用的是贪心本质,存在欠拟合风险。
4.1.1 优点
- 降低过拟合风险:由于预剪枝在决策树构建过程中就进行了剪枝,因此可以避免树过深导致的过拟合问题。
- 减少训练时间:通过提前停止树的生长,可以减少不必要的计算和分裂,从而缩短训练时间。
- 简单高效:预剪枝策略相对简单,易于实现和理解。
4.1.2 缺点
- 欠拟合风险:如果预剪枝过于严格,可能会导致决策树过于简单,无法学习到数据的全部特征,从而产生欠拟合现象。
- 难以确定合适的剪枝参数:预剪枝需要设置一些参数来控制树的生长,如最大深度、最小样本数等。这些参数的选择对模型的性能有很大影响,但通常很难确定最合适的参数值。
4.2 后剪枝(Post-pruning)
在决策树构建完成后进行剪枝,从底部向上对内部节点进行考察。如果将某个内部节点替换为叶节点能带来泛化性能的提升,那么就进行替换。后剪枝的具体操作是,先构造一颗完整的决策树,然后自底向上的对非叶节点进行考察。如果将该节点对应的子树替换为叶节点后,能够提升模型的泛化能力,那么就进行替换。
4.2.1 优点
- 欠拟合风险小:后剪枝是在决策树完全生长后再进行剪枝的,因此可以确保学习到数据的全部特征,降低欠拟合的风险。
- 泛化能力较强:通过删除一些不必要的子树,后剪枝可以提高决策树的泛化能力,使其更好地适应新的、未见过的数据。
4.2.2 缺点
- 训练开销大:后剪枝需要先构建一棵完整的决策树,然后再进行剪枝操作,因此训练时间通常比预剪枝长。
- 剪枝过程可能复杂:后剪枝需要遍历整棵树,并根据某种准则来判断是否剪枝。这个过程可能比较复杂,需要更多的计算资源。
4.3 剪枝相关API
在scikit-learn库中,决策树的剪枝通常是通过设置决策树生成器的参数来实现的,特别是通过max_depth、min_samples_split、min_samples_leaf、min_weight_fraction_leaf、max_leaf_nodes等参数来控制树的生长,从而达到剪枝的效果。
max_depth: 树的最大深度。设置为一个整数,可以防止树过深。min_samples_split: 分割内部节点所需的最小样本数。设置为一个整数,可以确保节点在进一步分割之前具有足够的样本。min_samples_leaf: 叶节点所需的最小样本数。设置为一个整数,可以防止树产生过小的叶子节点。min_weight_fraction_leaf: 叶节点所需的最小加权样本分数的阈值。这用于处理带权重的样本。max_leaf_nodes: 最大叶子节点数。设置为一个整数,可以直接限制树的叶子节点数量。
这些参数可以在构建决策树时通过DecisionTreeClassifier或DecisionTreeRegressor类的初始化函数来设置。
另外,scikit-learn也提供了DecisionTreeClassifier.cost_complexity_pruning_path和DecisionTreeRegressor.cost_complexity_pruning_path方法,用于计算不同复杂度参数下的剪枝路径,但这通常需要更高级的用户进行手动剪枝。
5 决策树API
5.1 分类决策树
sklearn.tree.DecisionTreeClassifier
主要参数:
criterion: 字符串,可选 'gini' 或 'entropy'(默认='gini')。用于分割特征的准则。'gini' 代表基尼不纯度(即cart算法),'entropy' 代表信息增益(即id3算法)。splitter: 字符串,可选 'best' 或 'random'(默认='best')。用于在每个节点选择分割的特征的策略。'best' 选择最佳分割,'random' 则随机选择。max_depth: 整数或None(默认=None)。树的最大深度。如果为None,则树会生长到所有叶子都是纯的或者所有叶子都包含少于min_samples_split的样本。min_samples_split: 整数或浮点数,在节点分割前所需的最小样本数(默认=2)。min_samples_leaf: 整数或浮点数,一个叶子节点所需的最小样本数(默认=1)。max_features: 整数、浮点数、字符串或None(默认=None)。用于在每次分割时考虑的特征的最大数量。random_state: 整数、RandomState实例或None(默认=None)。控制随机性的参数,用于在特征选择和样本划分时的随机性。
主要方法:
fit(X, y): 使用输入数据X和标签y来训练模型。predict(X): 使用训练好的模型对输入数据X进行预测。score(X, y): 返回给定测试数据和标签上的平均准确度。predict_proba(X): 对于分类问题,返回每个样本属于每个类别的概率。
5.2 回归决策树
sklearn.tree.DecisionTreeRegressor
主要参数(大部分与DecisionTreeClassifier相同):
criterion: 字符串,可选 'mse'、'friedman_mse'、'mae'(默认='mse')。用于分割特征的准则。'mse' 代表均方误差,'friedman_mse' 是改进版的均方误差,'mae' 代表平均绝对误差。
主要方法(与DecisionTreeClassifier相同):
fit(X, y): 使用输入数据X和目标值y来训练模型。predict(X): 使用训练好的模型对输入数据X进行预测。score(X, y): 返回给定测试数据和目标值上的R^2得分。
6 代码实现
# 导包
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier,plot_tree
from sklearn.metrics import classification_report# 1.导入数据
tatan_data = pd.read_csv('data/train.csv')
print(tatan_data.info())# 2.数据预处理
x = tatan_data[['Pclass', 'Age', 'Sex']]
y = tatan_data['Survived']
x = pd.get_dummies(x)
print(x.info)
x.fillna(x['Age'].mean(),inplace=True)
x_trian,x_test,y_train,y_test = train_test_split(x,y,train_size=0.8,random_state=1)# 4。模型训练
dt = DecisionTreeClassifier(criterion='gini')
dt.fit(x_trian,y_train)
# 5. 模型评估
print(dt.score(x_test, y_test))# 6.模型预测
y_ptedict = dt.predict(x_test)
print(classification_report(y_true=y_test, y_pred=y_ptedict))
# 7。可视化-可视化树结构
plt.figure(figsize=(30,20))
plot_tree(dt,filled=True,max_depth= 5,feature_names=['Pclass', 'Age', 'Sex_female', 'Sex_male'],
class_names=['died', 'survived'])
plt.show()
相关文章:
机器学习(五) ----------决策树算法
目录 1 核心思想 2 决策树算法主要步骤 3 决策树算法的分类 3.1 ID3算法(Iterative Dichotomiser 3): 3.1.1 基本步骤 3.1.2 原理 信息增益 3.1.3 注意事项 3.2 C4.5算法: 3.2.1. 信息增益率 计算公式 3.2.2. 构建决策…...

Redis的数据完全是存在内存中的吗?
是的,Redis的数据完全是存储在内存中的。这也是Redis能够提供非常高速的读写性能的主要原因,尤其适用于需要快速响应的应用场景。然而,虽然Redis将所有数据存储在内存中,但它也提供了持久化机制,可以将数据异步地保存到…...
Linux开发--Linux设备驱动核心
Author: cpu_codeDate: 2020-06-30 16:15:35LastEditTime: 2020-07-01 17:59:23FilePath: \md\Linux\6818_Linux驱动.mdGitee: https://gitee.com/cpu_codeCSDN: https://blog.csdn.net/qq_44226094 Linux设备驱动核心概念 Linux内核中断处理 Linux操作系统下同裸机程序一样…...

vue3引入vant完整步骤
在Vue 3中引入Vant(一个基于Vue的移动端UI组件库)的完整步骤通常包括以下几个部分: 安装Vue CLI(如果你还没有安装的话): npm install -g vue/cli 创建一个新的Vue项目: 假设你希望项目名为my…...

C语言——文件缓冲区
一、用户缓冲区和系统缓冲区 缓冲区的概念确实可以分为多个层次,其中最常见的两个层次是用户缓冲区和系统缓冲区。 这里的用户缓冲区和系统缓冲区都包括输入输出缓冲区。 1、用户缓冲区(User-space Buffer) 用户缓冲区是指由用户程序&…...
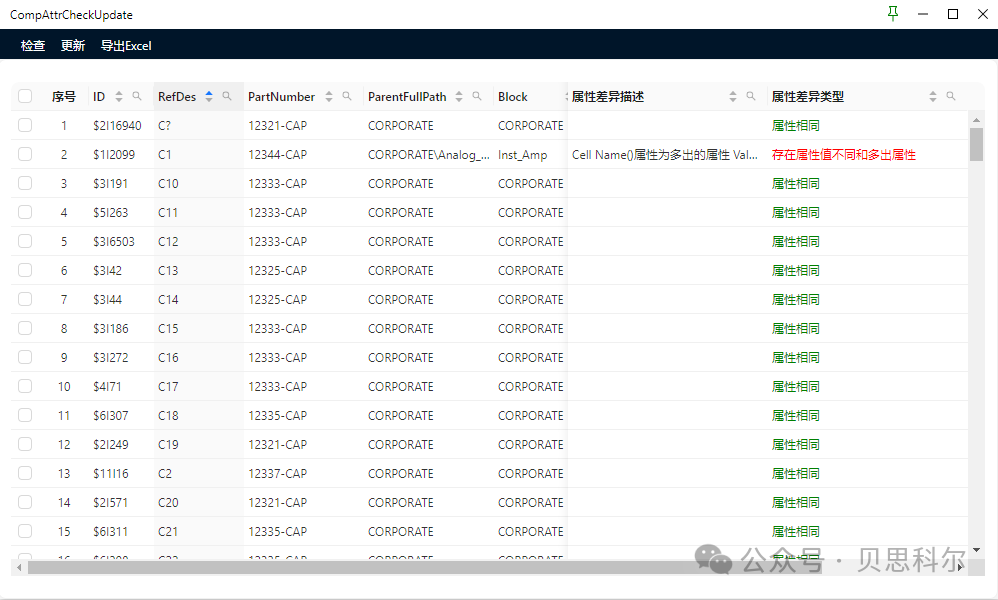
如何快速检测原理图中的元器件与PLM系统的一致性,提高原理图设计准确性
背景介绍 保证原理图中的元器件来源于公司的PLM系统、ERP系统的,是输出有效BOM的根源,初始BOM的准确率,能大大降低ECN的数量,提高生产备料的时效,缩短采购周期。 然而,原理图设计过程中,由于…...

英特尔处理器排行
英特尔的处理器性能排行通常是根据其发布的不同代数和型号来划分的,以下是一些高性能的英特尔处理器: Intel 酷睿 i9 14900K:这是目前英特尔桌面平台中的旗舰处理器之一,提供了极高的性能,适合高端游戏和专业工作负载…...

【日志革新】在ThinkPHP5中实现高效TraceId集成,打造可靠的日志追踪系统
问题背景 最近接手了一个骨灰级的项目,然而在项目中遇到了一个普遍的挑战:由于公司采用 ELK(Elasticsearch、Logstash、Kibana)作为日志收集和分析工具,追踪生产问题成为了一大难题。尽管 ELK 提供了强大的日志分析功…...
)
英译汉早操练-(二十)
hello大家好,这篇跟随十九,继续真题学习。如果想看全部请返回到第十九篇。 英译汉早操练-(十九)-CSDN博客 The political upheaval in Libya and elsewhere in North Africa has opened the way for thousands of new migrants to…...
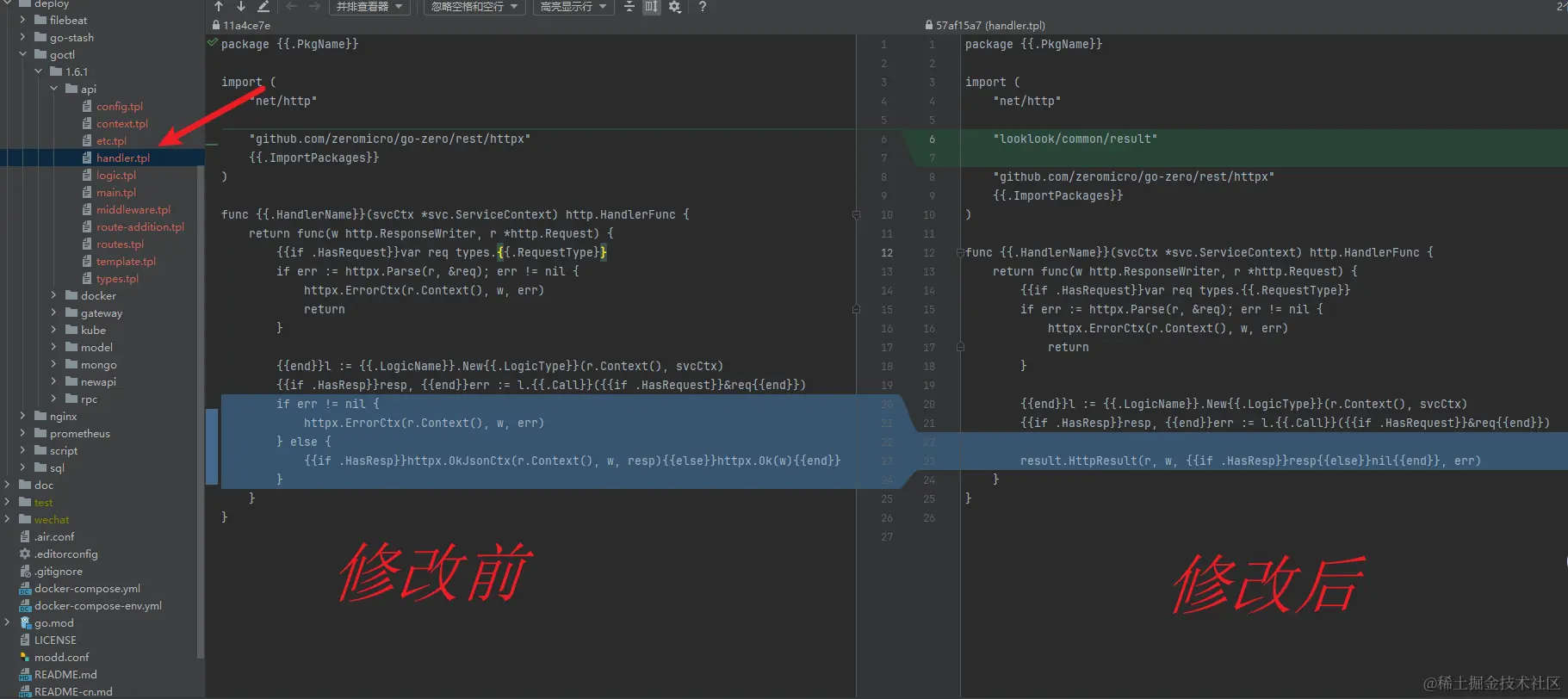
Go-Zero自定义goctl实战:定制化模板,加速你的微服务开发效率(四)
前言 上一篇文章带你实现了Go-Zero和goctl:解锁微服务开发的神器,快速上手指南,本文将继续深入探讨Go-Zero的强大之处,并介绍如何使用goctl工具实现模板定制化,并根据实际项目业务需求进行模板定制化实现。 通过本文…...

(五)STM32F407 cubemx IIC驱动OLED(1)IIC协议篇
(五)STM32F407 cubemx IIC驱动OLED(1)IIC协议篇 这篇文章主要是个人的学习经验,想分享出来供大家提供思路,如果其中有不足之处请批评指正哈。 废话不多说直接开始主题,本人是基于STM32F407V…...

OpenCV特征匹配总结
1.概述 在深度学习出现之前,图像中的特征匹配方法主要有 2.理论对比 3.代码实现 #include <iostream> #include <opencv2/opencv.hpp>int main(int argc, char** argv) {if(argc ! 3) {std::cerr << "Usage: " << argv[0] <…...
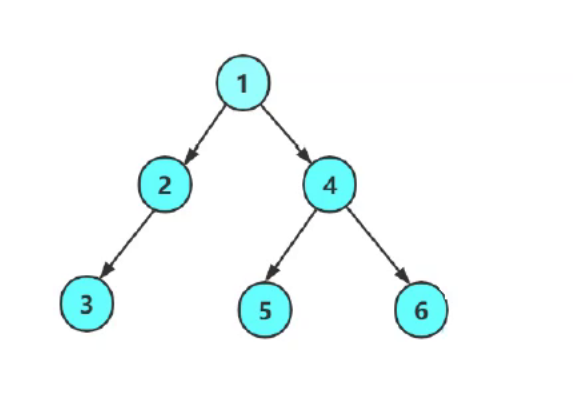
二叉树的四种遍历代码实现
二叉树的遍历大致能分为以下几种 1.前序:根 左 右 2.中序:左 根 右 3.后序:左 右 根 4.层序:从根开始一层一层的向下 如上图访问顺序: 前序:1 2 3 N N N 4 5 N N 6 N N 中序:N 3 N 2 N 1 N 5 N 4 N …...

系统和功能测试:确保软件的功能和易用性
目录 概述 功能测试 LOSED 模型 用例的设计 等价类划分 边界值分析 循环结构测试的综合方法 因果图 决策表 功能图 正交实验设计 易用性测试 内部易用性测试 外部易用性测试 功能性测试 正向功能性测试 负向功能性测试 功能性测试工具 结语 概述 在软件开发…...

关于服务端接口知识的汇总
大家好,今天给大家分享一下之前整理的关于接口知识的汇总,对于测试人员来说,深入了解接口知识能带来诸多显著的好处。 一、为什么要了解接口知识? 接口是系统不同模块之间交互的关键通道。只有充分掌握接口知识,才能…...
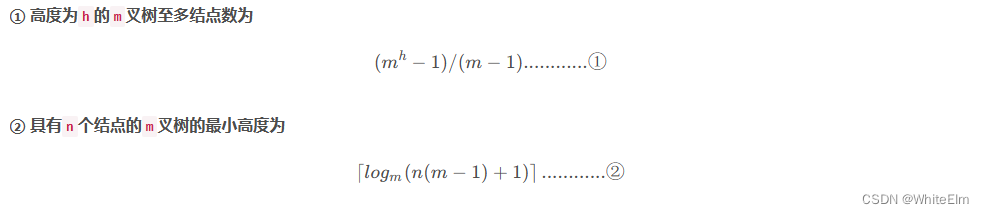
树(数据结构)
树的定义 一个根结点,其余结点分为 m 个不相交的集合, 其中每个集合本身又是一棵树,并且称为根的子树。 树的根结点没有前驱,其他结点有且仅有一个前驱。 所有结点可以有0个或多个后继。 基本术语 结点的度 树的度 : 树…...
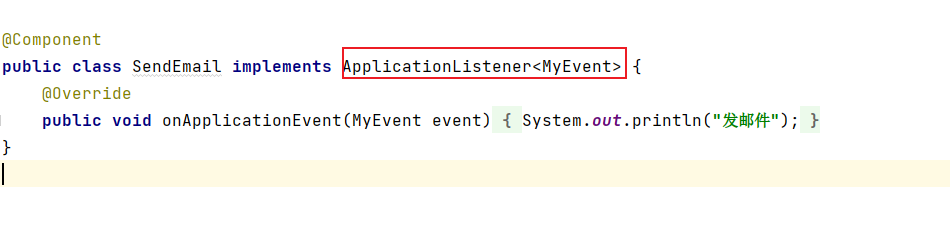
Spring底层入门(十一)
1、条件装配 在上一篇中,我们介绍了Spring,Spring MVC常见类的自动装配,在源码中可见许多以Conditional...开头的注解: Conditional 注解是Spring 框架提供的一种条件化装配的机制,它可以根据特定的条件来控制 Bean 的…...
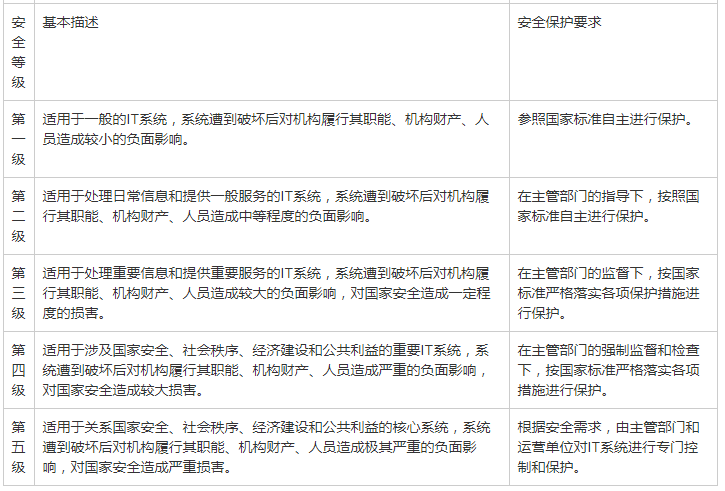
优质资料:大型制造企业等级保护安全建设整改依据,系统现状分析,网络安全风险分析
第1章 项目概述 XX 大型制造型企业是国内一家大型从事制造型出口贸易的大型综合企业集团,为了落实国家及集团的信息安全等级保护制度,提高信息系统的安全防护水平,细化各项信息网络安全工作措施,提升网络与信息系统工作的效率&am…...

几种监控工具学习
在Linux上有很多监控工具,比如Zabbix、Prometheus、APM和ELK 监控工具是确保系统稳定运行的关键组件之一,它可以帮助系统管理员和开发人员及时发现并解决问题。 以下是几种流行的监控工具的简要介绍: Zabbix: Zabbix 是一个企…...

树莓派python开发
树莓派自带thonny 点亮LED灯 import RPi.GPIO as GPIO import time# 设置GPIO模式为BCM GPIO.setmode(GPIO.BCM)# 设置LED引脚 led_pin 18# 设置LED引脚为输出 GPIO.setup(led_pin, GPIO.OUT)# 点亮LED GPIO.output(led_pin, GPIO.HIGH)# 延时2秒 time.sleep(2)# 关闭LED GPI…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...
