代码随想录算法训练营Day 41| 动态规划part03 | 343. 整数拆分、96.不同的二叉搜索树
代码随想录算法训练营Day 41| 动态规划part03 | 343. 整数拆分、96.不同的二叉搜索树
文章目录
- 代码随想录算法训练营Day 41| 动态规划part03 | 343. 整数拆分、96.不同的二叉搜索树
- 343. 整数拆分
- 一、动态规划
- 二、贪心(不需要掌握)
- 96.不同的二叉搜索树
- 一、动态规划
343. 整数拆分
题目链接
- 确定dp数组以及下标的含义
dp[i]:分拆数字i,可以得到的最大乘积为dp[i]。- 确定递推公式
想要求dp[i][j],只能有两个方向来推导出来,即dp[i - 1][j] 和 dp[i][j - 1]
状态转移方程 dp[i][j] = dp[i - 1][j] + dp[i][j - 1];- dp数组如何初始化
dp[i][0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0][j]也同理;
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;- 确定遍历顺序
看一下递推公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1],dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。- 打印dp数组
一、动态规划
class Solution(object):def integerBreak(self, n):""":type n: int:rtype: int"""dp=[0]*(n+1)dp[1]=1dp[2]=1for i in range(3,n+1):for j in range(1,i): # 优化版本可以写为 for j in range(1,i//2+1)dp[i]=max(j*dp[i-j],j*(i-j),dp[i])return dp[n]
二、贪心(不需要掌握)
class Solution:def integerBreak(self, n):if n == 2: # 当n等于2时,只有一种拆分方式:1+1=2,乘积为1return 1if n == 3: # 当n等于3时,只有一种拆分方式:2+1=3,乘积为2return 2if n == 4: # 当n等于4时,有两种拆分方式:2+2=4和1+1+1+1=4,乘积都为4return 4result = 1while n > 4:result *= 3 # 每次乘以3,因为3的乘积比其他数字更大n -= 3 # 每次减去3result *= n # 将剩余的n乘以最后的结果return result
96.不同的二叉搜索树
题目链接
- 确定dp数组以及下标的含义
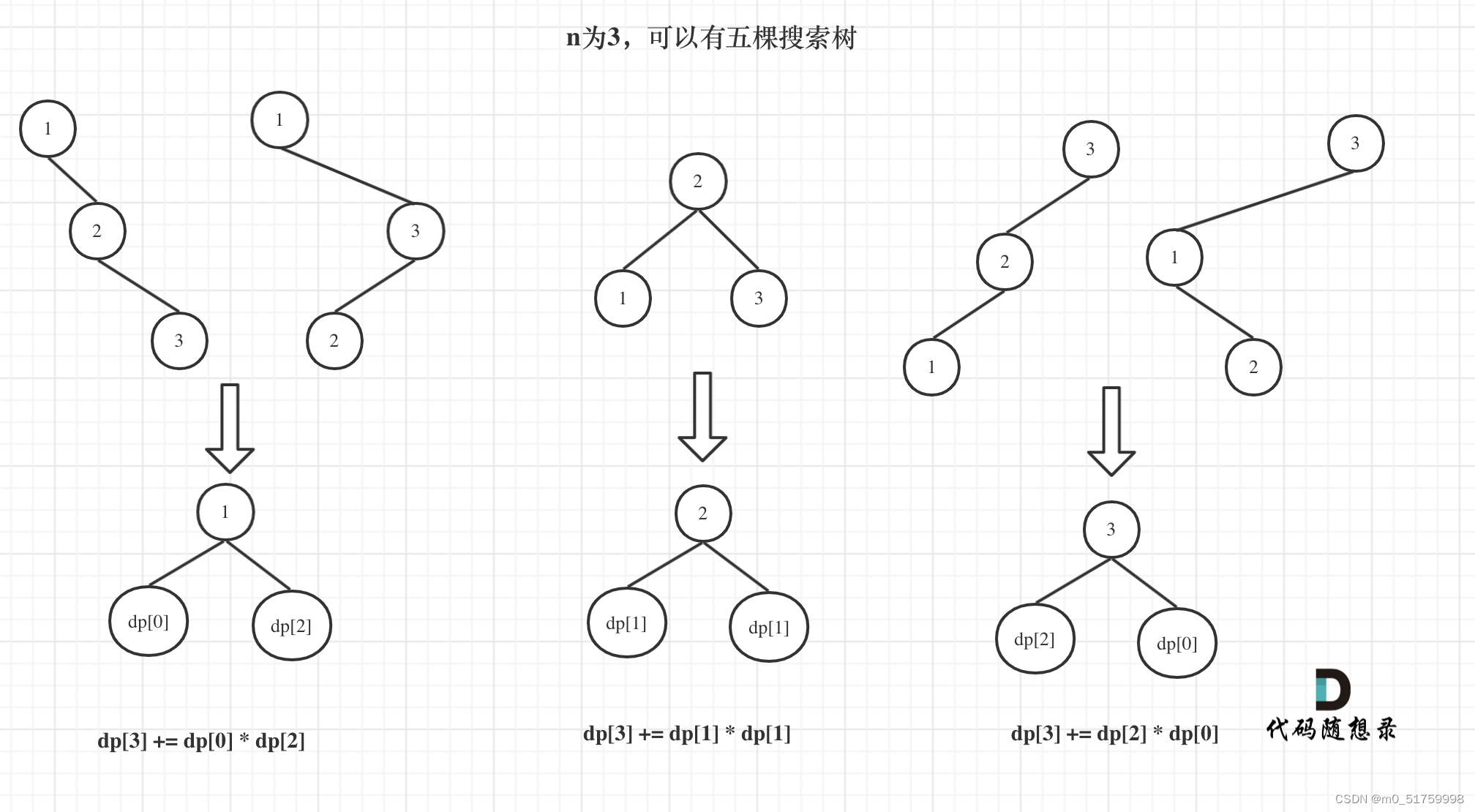
dp[i] : 1到i为节点组成的二叉搜索树的个数为dp[i]- 确定递推公式
, dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]
j相当于是头结点的元素,从1遍历到i为止。
所以递推公式:dp[i] += dp[j - 1] * dp[i - j]; ,j-1 为j为头结点左子树节点数量,i-j 为以j为头结点右子树节点数量- dp数组如何初始化
d从定义上来讲,空节点也是一棵二叉树,也是一棵二叉搜索树
从递归公式上来讲,dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量] 中以j为头结点左子树节点数量为0,也需要dp[以j为头结点左子树节点数量] = 1, 否则乘法的结果就都变成0了。
所以初始化dp[0] = 1- 确定遍历顺序
首先一定是遍历节点数,从递归公式:dp[i] += dp[j - 1] * dp[i - j]可以看出,节点数为i的状态是依靠 i之前节点数的状态。- 打印dp数组
一、动态规划
class Solution(object):def numTrees(self, n):""":type n: int:rtype: int"""dp=[0]*(n+1)dp[0]=1 # 当n为0时,只有一种情况,即空树,所以dp[0] = 1for i in range(2,n+1):# 遍历从1到n的每个数字for j in range(1,i+1): # 对于每个数字i,计算以i为根节点的二叉搜索树的数量dp[i] += dp[j-1]*dp[i-j] # 利用动态规划的思想,累加左子树和右子树的组合数量return dp[n]
相关文章:

代码随想录算法训练营Day 41| 动态规划part03 | 343. 整数拆分、96.不同的二叉搜索树
代码随想录算法训练营Day 41| 动态规划part03 | 343. 整数拆分、96.不同的二叉搜索树 文章目录 代码随想录算法训练营Day 41| 动态规划part03 | 343. 整数拆分、96.不同的二叉搜索树343. 整数拆分一、动态规划二、贪心(不需要掌握) 96.不同的二叉搜索树一…...
多模态产品在智能文档处理应用的展望------以TextIn模型为例
前言发展现状TextIn 文档解析技术文本向量化展望合合信息 前言 第十四届视觉与学习青年学者研讨会(VALSE 2024)于5月5日-7日在山城重庆渝北区悦来国际会议中心举办。大会聚焦计算机视觉、模式识别、多媒体和机器学习等领域的国际前沿和热点方向。大会中,合合信息智能…...

上海市计算机学会竞赛平台2024年3月月赛丙组最近的数字
题目描述 给定两个正整数 𝑛n 与 𝑑d ,请找到所有最接近 𝑛n 且是 𝑑d 的倍数的整数。 输入格式 第一行:单个整数表示 𝑛n第二行:单个整数表示 𝑑d 输出格式 若干行…...

RFID在汽车制造中的应用如何改变行业
随着工业4.0和中国制造2025的推进,企业对于智能化、自动化的需求日益增长,RFID射频技术在制造业中已经相当普遍了。在如今这瞬息万变的行业与时代中,RFID技术可以帮助企业获得竞争优势,简化日益复杂的生产流程,推动企业…...

sCrypt受邀在中国人民大学举办《区块链与数字经济》课程讲座
4月17日,可一科技特邀美国sCrypt公司的开发工程师周全,在中国人民大学的《区块链与数字经济》课程上进行了讲座。周全讲解了区块链的分布式设计、不可篡改特性,以及智能合约的基本原理,利用“智能家居触发机制”等生动比喻&#x…...

pc端的鼠标箭头变换
<div style"cursor:pointer"></div>...

ICode国际青少年编程竞赛- Python-2级训练场-for循环练习2
ICode国际青少年编程竞赛- Python-2级训练场-for循环练习2 1、 for i in range(5):Dev.step(9 - i * 2)Dev.turnLeft()2、 for i in range(3):Spaceship.step(i 1)Spaceship.turnRight()Spaceship.step(i 1)Spaceship.turnLeft()3、 for i in range(4):Dev.step(10 - i…...
RiPro主题美化【支付弹窗底部提示语根据入口不同有不同的提示】ritheme主题美化RiProV2 增加支付提示语,按支付类型不同,入口不同提示语不同的设置
RiPro主题美化【支付弹窗底部提示语根据入口不同有不同的提示】ritheme主题美化RiProV2 增加支付提示语,按支付类型不同,入口不同提示语不同的设置 背景: 接上文:https://www.uu2id.com/827.html 付费组件在以下几个地方会弹出:1)文章隐藏内容付费;2)付费资源下载;3…...

MSMQ消息队列
MQ是一种企业服务的消息中间节技术,这种技术常常伴随着企业服务总线相互使用,构成了企业分布式开发的一部分,如果考虑到消息的发送和传送之间是可以相互不联系的并且需要分布式架构,则可以考虑使用MQ做消息的中间价技术࿰…...
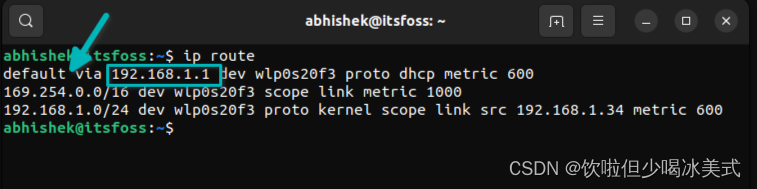
树莓派nmap扫描
debian系统安装nmap: sudo apt install nmap安装nmap完成后,输入 ip route 来查看当前Wi-Fi路由器的ip地址。 第一行的default via后显示的便是网关地址,也就是路由器地址。 获取到路由器ip地址后,在终端中输入: …...
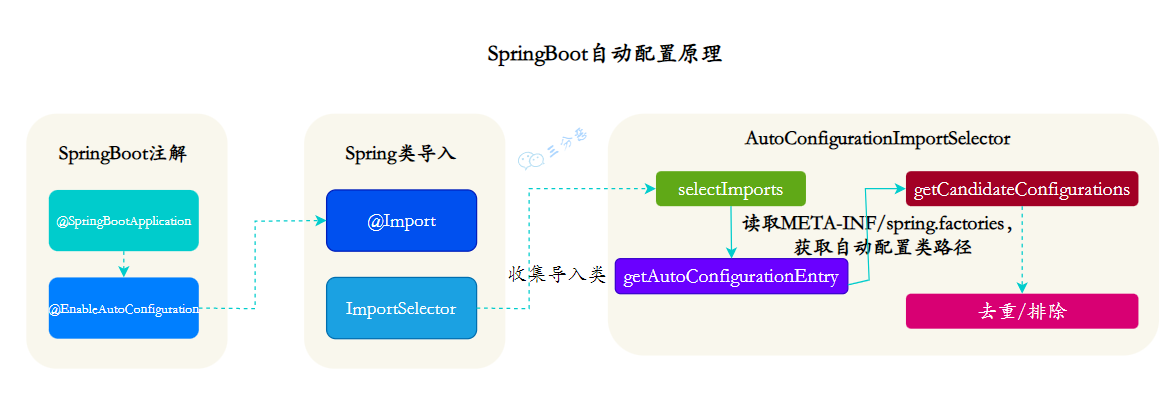
【必看】Spring系列面试题
Spring Core Container, AOP, Data Access, Web... 基础 1. 简单介绍Spring 一款开源的轻量级 Java 开发框架,旨在提高开发人员的开发效率以及系统的可维护性。Spring 支持 IoC(Inversion of Control:控制反转) 和 AOP(Aspect-Oriented Pro…...

wordpress增加谷歌分析
wordpress增加谷歌分析 为了更好的浏览体验,欢迎光顾勤奋的凯尔森同学个人博客 http://www.huerpu.cc:7000 一、创建谷歌分析账号与媒体应用 谷歌分析地址:https://analytics.google.com/analytics 创建一个账号,如果你没有的话。 在该账…...
linux的信号量的使用
1.信号量 在多线程情况下,线程要进入关键代码就得获取信号量(钥匙){sem_init(&sem, 0, 0);},没有信号量的情况下就一直等待sem_wait(&sem),只到别人把钥匙(sem_post(&sem))给你。 …...

C--贪吃蛇
前言 贪吃蛇游戏是一个耳熟能详的小游戏,本次我们讲解他的简单的实现,需要掌握基本的API知识(http://t.csdnimg.cn/uHH6y),简单的C语言知识和基本的数据结构链表 简单的准备工作 蛇的节点 在游戏运⾏的过程中,蛇每次吃⼀个⻝物,蛇的⾝体就会变⻓⼀节&a…...

element ui的确认提示框按钮样式修改
修改确认提示框的默认按钮样式,使用css强制修改 例: js代码: this.$confirm("您确定要删除吗?此操作无法撤销并且将永久删除所有数据。", "提示", { type: "warning", cancelButtonClass: "…...

【vue】keep-alive:true缓存导致页面数据不刷新
keep-alive生命周期钩子函数:activated、deactivated activated:页面第一次进入的时候,钩子触发的顺序是created->mounted->activated deactivated: 页面退出的时候会触发deactivated, 当再次前进或者后退的时候只触发acti…...

Golang — map的使用心得和底层原理
map作为一种基础的数据结构,在算法和项目中有着非常广泛的应用,以下是自己总结的map使用心得、实现原理、扩容机制和增删改查过程。 1.使用心得: 1.1 当map为nil和map为空时,增删改查操作时会出现的不同情况 我们可以发现&#…...
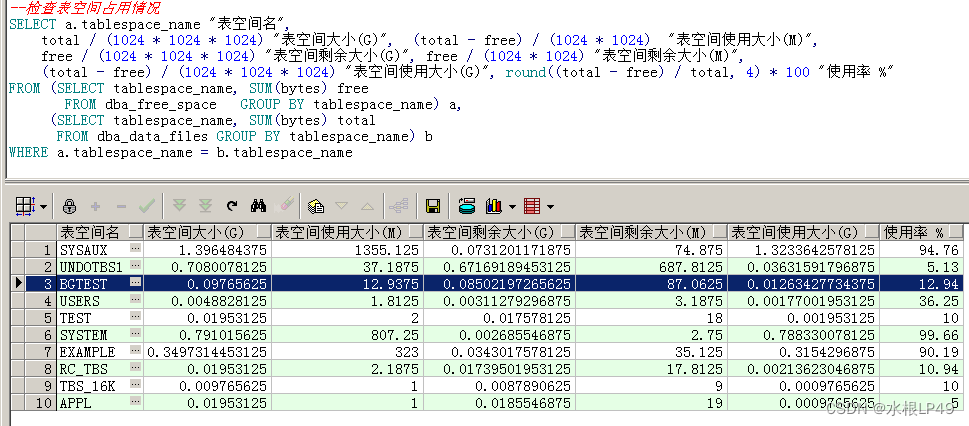
Oracle如何收缩减小表空间大小
比如我们发现一个表空间占用比较大,但是空闲空间很大,想要减小表空间占用大小。查看表空间的情况 发现BETEST表空间占用大,但是剩余大小比较大,可以减小存储占用。 如果我们想减小到100MB,那么就登录其用户执行&#…...
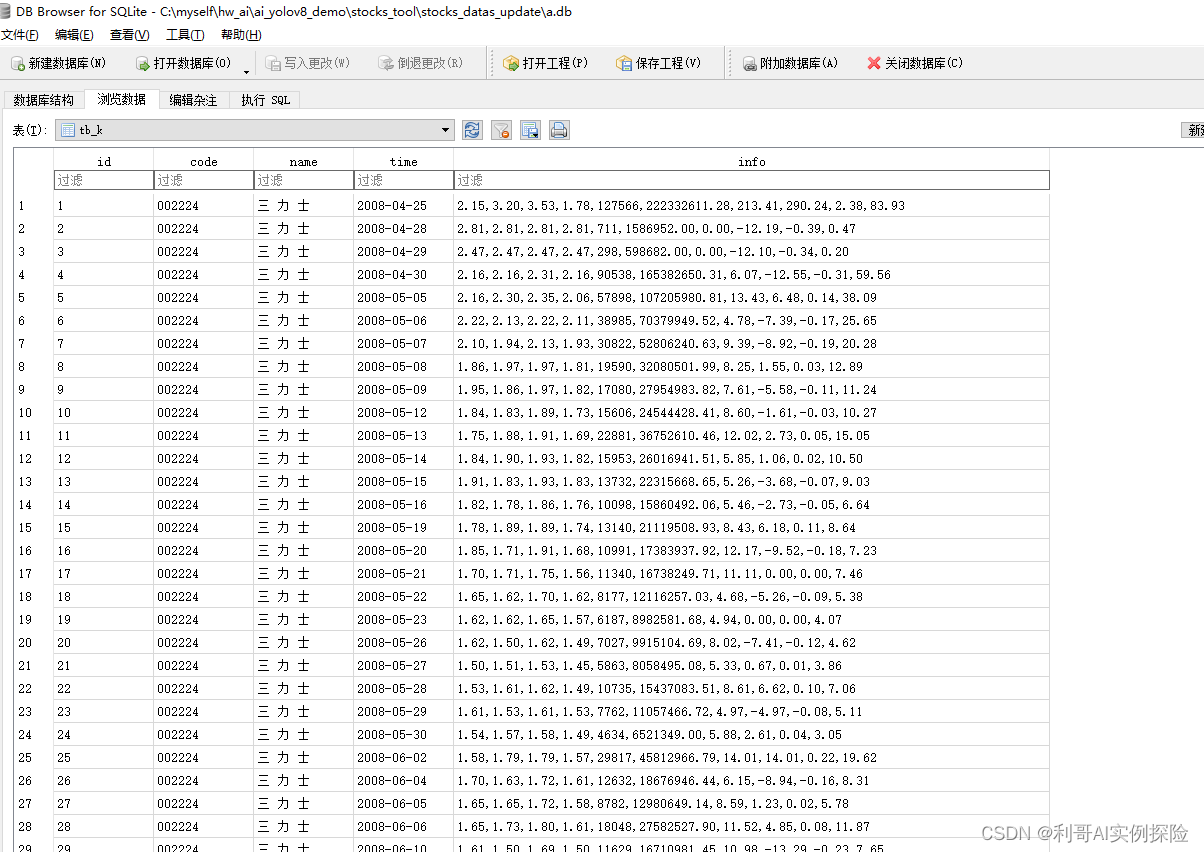
【爬虫】爬取股票历史K线数据写入数据库(三)
前几天有写过两篇: 【爬虫】爬取A股数据写入数据库(二) 【爬虫】爬取A股数据写入数据库(一) 现在继续完善,分析及爬取股票的历史K线数据通过ORM形式批量写入数据库。 2024/05,本文主要内容如下…...

文心一言指令
文心一言(ERNIE Bot)是百度公司开发的人工智能语言模型,它可以接收各种指令来执行不同的任务。以下是一些可能的指令示例: 知识问答: 指令:“请问什么是人工智能?”文心一言会回答关于人工智能…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...
