CTF-密码学基础
概述

-
密码学(Cryptolopy):是研究信息系统安全保密的科学
-
密码学研究的两个方向:
- 密码编码学(Cryptography):主要研究对信息进行编码,实现对信息的隐蔽
- 密码分析学(Cryptanalytics):主要研究加密信息的破译或消息的伪造
-
具体作用:
- 提供保密性——密码技术可用于加解密
- 用于鉴别——解决身份冒充的问题
- 消息的接收者能够确认消息的来源,发送者不可能伪装成他人
- 发送者也要能够确认接收者是否是自称的,接收者不可能伪装成他人
- 提供完整性——解决篡改问题
- 消息的接收者应该能够验证在传递过程中消息没有被修改
- 抗抵赖
- 发送者或接收者事后不可虚假地否认其发送或接收到的信息
古典密码
- 古典密码体制比较简单,容易破解,但了解它们的设计原理对理解、设计和分析现代密码体制十分重要
- 古典密码体制的核心思想:代替和置换
- 代替:将明文中的每一个字符替换成另一个字符从而形成密文
- 置换:重新排列明文消息中元素的位置而不改变元素本身从而形成密文
单表代换密码
- 明文中所有字母的加密都使用同一个映射关系:
- 设 S p S_p Sp是明文字母空间, S c S_c Sc是密文字母空间
- 映射关系 f : S p − > S c f:S_p->S_c f:Sp−>Sc
- 一般情况下,f是一一映射,即对相同的明文字母映射为相同的密文字母
棋盘密码

——这只是其中一个例子,这里棋盘排列是可以随意按加密人的想法进行排列

移位密码


当key=3时的移位密码,又称为“凯撒密码”
代换密码

仿射密码

- k 1 k_1 k1与 k 2 k_2 k2是后续需要选定的值



多表代换密码
维吉尼亚密码

- 先得到密钥字和对应的key
- 明文按密钥字长度进行划分
- 明文本身的数字+密钥对应数字 mod 26得到对应的字母

由于引入的密钥字,因此同一个明文字母可以被映射为不同的密文字母
希尔密码
- 一种基于矩阵运算的加密算法



比较分析
- 单表代换密码体制中,明文中单字母出现的频率分布与密文中相同。这会带来密码的安全性问题,比如我们就可以通过频率分布来推测对应的字母是什么
- 在维吉尼亚密码和希尔密码体制中,将明文进行分组,对每组成组进行替换,使得同一个明文字母可以对应不同的密文,改变了单表代换密码中密文的唯一性
置换密码
- 在代换密码中,可以认为明文中各字母的相对顺序在加密成密文后仍保持不变,只是将它们用其他符号代替
- 置换密码是,通过改变明文中各元素的相对位置来进行加密,但元素本身的取值或内容形式不变

- 按m个数,将明文分组,每组m个字符
- 然后按照pai的位置放置,比如i放3号位,n放1号位,f放4号位,o放2号位,依次得到密文
密码学抽象概念
- 香农在论文《保密系统的通信理论》中提出的保密通信模型:

-
通信中的参与者
- 发送者:在双方交互中合法的信息发送实体
- 接收者:在双方交互中合法的信息接收实体
- 分析者:破坏通信接收和发送双方正常安全通信的其他实体
-
明文和密文
- 明文或消息(plaintext,message):
- 尚未隐藏或未被加密的信息,用P或M表示
- 明文的集合称为明文信息空间,用 S p S_p Sp表示
- 密文(ciphertext):
- 被加密(encryption)后的消息称为密文,用C表示
- 所有密文构成密文信息空间,用 S c S_c Sc表示
- 明文或消息(plaintext,message):
-
密钥
- 明文到密文的转换由一些特殊函数完成,控制这些函数的参数称为密钥key,用K表示
- 一般是由用户事先选定的较短的字符或数字序列
- 所有的密钥集合构成密钥空间,用 S k S_k Sk表示
- 密钥空间中不相同密钥的个数称为密钥体制的密钥量,它是衡量密码体制安全性的一个重要指标
- 一般情况下,密钥长度越大,密文越安全,但是加密速度越慢
-
加密
-
在密钥K的作用下,把明文P从Sp对应到Sc的一种变换
E k : S p − > S c E_k:S_p->S_c Ek:Sp−>Sc -
则明文和密文的关系可表示为
C = E k ( P ) C=E_k(P) C=Ek(P)
-
-
解密
-
加密变换的逆变换,把密文C从Sc对应到Sp
D k : S c − > S p P = D k ( C ) = D k ( E k ( P ) ) D_k:S_c->S_p\\ P=D_k(C)=D_k(E_k(P)) Dk:Sc−>SpP=Dk(C)=Dk(Ek(P)) -
信息的保密性依赖于密钥K的保密性
-
-
密码体制:
一个完整的密码体制(cryptosystem)由5部分组成
- 明文信息空间Sp
- 密文信息空间Sc
- 密钥空间Sk
- 加密变换族Ek
- 解密变换族Dk
-
信道:
从一个实体向另一个实体传递信息的通路
- 安全信道:分析者没有能力对其上的信息进行阅读、删除、修改、添加的信道
- 公共信道:分析者可以任意对其上的信息进行阅读、删除、修改、添加的信道
攻击手段

现代密码

- 古典密码:数据的安全基于算法的保密
- 现代密码:数据的安全基于密钥,算法公开
- 判断现代密码的标准:加密算法应建立在算法公开不影响明文和密钥安全的基础上
现代密码体制的一种分类方法
根据对明文的处理方法不同分为分组密码和流密码:
- 分组密码:将明文分成固定长度的组,用同一密钥和算法对每一组加密,输出也是固定长度的密文
- 流密码:每次加密一位或一字节的明文
散列哈希函数

MD算法家族
- MD5目前主要的用途:
- 一致性验证
- 数字签名
- 安全访问认证
- ……
SHA家族
- 与MD5类似
- 美国国家标准密码体系
- 主要应用领域:
- 主要用于SSL\TTL等证书数字签名,用于可信第三方签发身份验证信息
SM家族
- 中国国家标准密码体系
- SM1是对称加密。其加密强度与AES相当。该算法不公开,调用该算法时,需要通过加密芯片的接口进行调用
- SM2是非对称加密,基于ECC
- SM3信息摘要,可以用MD5作为对比理解,算法已公开,校验结果为256位
- SM4无线局域网标准的分组数据算法。对称加密,密钥长度和分组长度均为128位
MD5算法详解
雪崩效应
- 虽然Hash函数的散列值空间远小于输入空间,但是哈希函数对于数据的改变具有极高的敏感性
- 1Bit数据的改变会造成散列值极大的改变
具体流程
-
处理原文,对原文进行数据填充,使得消息长度对512取模得到448
设消息长度为 X ,即满足 X m o d 512 = 448 设消息长度为X,即满足Xmod \ 512=448 设消息长度为X,即满足Xmod 512=448
填充方法在原文后面进行填充,填充第一位为1,其余为0 -
添加消息长度,在第一步结果之后再填充上原消息的长度,可用来进行存储的长度为64位(512-448)
如果消息长度大于 2 64 2^{64} 264,则只使用其低64位的值,即消息长度对2^64取模
在此步骤进行完毕后,最终消息长度就是512的整数倍

-
设置初始值,MD5的散列值长度位为128位,按每32位分成一组,一共4组
这4组的结果是由4个初始值A/B/C/D经过多轮(轮数由输入的信息长度决定)不断演变得到
-
循环运算(MD5算法核心)



对称加密算法
- 分组密码就是对称密码体制的一种形式,加解密的密钥相同


n是输出块的长度,m是输入块的长度
- 若n>m,则为有数据扩展的分组密码
- 若n<m,则为有数据压缩的分组密码
- 若n=m,则为无数据扩展也无压缩的分组密码
DES密码
- 总体结构
- 分组长度为64位
- 循环次数位16
- 密钥长度位64位(包括8位奇偶校验位)

- 总体描述
- 初始置换IP,将64位明文分为两个部分
- 之后进行16轮加密运算,称为函数f
- 最后进行末尾置换 I P − 1 IP^{-1} IP−1为初始置换的逆运算

非对称加密算法
RSA算法
先阐述几个概念
- 质数:只能被1和他本身整除的自然数
- 互质数:公约数只有1的两个数
- 同余运算:给定正整数m,如果两个整数a和b满足a-b能被m整除,即 ( a − b ) m o d m = 0 (a-b)mod\ m=0 (a−b)mod m=0,那么就称整数a与b对模m同余


加密示例

解密示例

密钥生成算法



CTF常见编码
BASE家族

Base16编码之后的特征:还有字符A~F还有数字0~9

Base32编码之后的特征:有数字A~Z,还有数字2~7,还有=号

URL编码
-
URL编码是一种浏览器用来打包表单输入的格式
-
URL编码就是一个字符ASCII码的十六进制。需要前面加上%
比如”\“,它的ASCII码是92,92的十六进制是5c,所以”\“的URL编码是%5c
-
URL编码的特征就是”%“加上2位16进制数
Unicode编码
- Unicode是计算机科学领域里的一项业界标准,包括字符集、编码方案等
- 你好 ——>\u4f60\u597d
- Unicode编码的特征就是”\u“加上4位16进制数
莫斯密码
-
具体内容可以查看隐写术中涉及的音频隐写部分
CTF-隐写术-CSDN博客

CTF密码学实战
编码题解题思路
- 一般没有密钥的就是编码题
- 编码题对密文的特征进行分析
- 通常不会作为单独的考题出现,一般是出现在其中的某一步

因为密文中有大写字母,小写字母,因此第一反应可以通过Base64进行解码,最后得到flag

根据题目回旋13的提示,移位算法rot13解码,即可得到答案

RSA算法解题

- 压缩包文件有两个,一个flag.enc是密文的二进制文件,一个是pubkey.pem是公钥
- 通过公钥来获取私钥,来解密这个加密之后的二进制文件
-
私钥第一步要解决的是,如何求到p和q
我们先用openssl工具把公钥文件进行解析

-
获取到了16进制的相乘的值,我们可以利用python等工具,将十进制转换出来

-
获取到十进制数后,我们利用工具yafu来寻找p和q,这一步一般需要比较长的时间
GitHub - bbuhrow/yafu: Automated integer factorization
.\yafu-Win32.exe factor(放入十进制数)
-
然后我们知道了p,q,n,e 现在求解d——可以在网上找,也可以自己写脚本文件
import gmpy2 import rsa p= q= n=相乘的大n数 e=65537 d=int(gmpy2.invert(e,(p-1)*(q-1))) privatekey=rsa.PrivateKey(n,e,d,p,q) with open("密文二进制文件地址","rb") as f:print(rsa.decrypt(f.read(),privatekey).decode())
未知编码方式解题思路
- 使用搜索引擎搜索部分密文,可能能够搜索到编码方式(抽象)
相关文章:

CTF-密码学基础
概述 密码学(Cryptolopy):是研究信息系统安全保密的科学 密码学研究的两个方向: 密码编码学(Cryptography):主要研究对信息进行编码,实现对信息的隐蔽密码分析学(Cryptanalytics):主要研究加密信息的破译或消息的伪造…...

代码随想录算法训练营day22 | 654.最大二叉树、617.合并二叉树、700.二叉搜索树中的搜索、98.验证二叉搜索树
654.最大二叉树 和构造二叉树差不多,本题使用索引的方式 class Solution:def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:return self.traversal(nums, 0, len(nums)-1)def traversal(self, nums, left, right):if left > r…...

企业信息防泄漏软件分析:盘点常用企业信息防泄漏软件
在当今数字化时代,企业信息防泄漏软件已成为保障企业数据安全不可或缺的一环。市面上众多的防泄漏软件各具特色,如何从中挑选出最适合自己企业的产品,成为了一个值得深入探讨的话题。 一、企业信息防泄漏软件分析 首先,我们需要…...

Rancher-Kubewarden-保姆级教学-含Demo测试
一、什么是Kubewarden? What is Kubewarden? | Kubewarden 1、就是容器集群的准入策略引擎。 1、使用的策略其实就是k8s原生的security context. 2、使用WebAssembly来编写策略。 1、WebAssembly,可以使用擅长的开发语言来编写策略。(下面的…...

Lumerical Script ------ array 数组类型 和 matrix 矩阵类型
Lumerical Script ------ array 数组类型 和 matrix 矩阵类型 引言正文array 数组类型matrix 矩阵类型引言 这篇仅仅用作个人笔记,因为作者本人比较擅长 Python,每次写 Lumerical Script 总是会写错代码。 正文 array 数组类型 Lumerical Script 脚本有些像 Matlab 脚本,…...
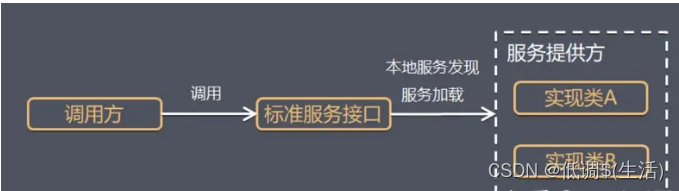
Springboot自动装配源码分析
版本 <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>2.3.4.RELEASE</version><relativePath/> <!-- lookup parent from repository --> </par…...
模型详解 动图讲解)
Visual Transformer (ViT)模型详解 动图讲解
1 Vit简介 1.1 Vit的由来 ViT是2020年Google团队提出的将Transformer应用在图像分类的模型,虽然不是第一篇将transformer应用在视觉任务的论文,但是因为其模型“简单”且效果好,可扩展性强(scalable,模型越大效果越好),成为了transformer在CV领域应用的里程碑著作,也…...
(std::forward))
C++:完美转发(一)(std::forward)
一、理解引用折叠 (一)引用折叠 1. 在C中,“引用的引用”是非法的。像 auto& &rx x;(注意两个&之间有空格)这种直接定义引用的引用是不合法的,但是编译器在通过类型别名或模板参数推导等语境…...

西部首个全域直播基地,打造西部直播基地领军形象
天府锋巢直播产业基地作为西部直播产业的领军者,以其前瞻性的战略布局和卓越的服务体系,正加速推动全域直播的快速发展,助力直播产业实现新升级。该基地作为成都规模最大的直播基地,以加快全域直播为核心目标,通过促进…...

钟表——蓝桥杯十三届2022国赛大学B组真题
问题分析 这个问题的关键有两点:1.怎么计算时针,分针,秒针之间的夹角,2.时针,分针,秒针都是匀速运动的,并非跳跃性的。问题1很好解决看下面的代码就能明白,我们先考虑问题2…...

CSS 之 圆形波浪进度条效果
一、简介 本篇博客讲述了如何实现一个圆形波浪进度条的样式效果,具体效果参考下方GIF图。该样式的加载进度条可以用在页面跳转或数据处理等情况下的加载动画,比起普通的横条进度条来说,样式效果更生动美观。 实现思路: 这…...
)
按下鼠标进行拖拽,让元素跟随鼠标进行移动,鼠标抬起,元素停止移;js鼠标拖拽 (鼠标按下事件:onmousedown、鼠标移动事件:onmousemove、鼠标抬起事件:onmouseup)
需求如下: 按下鼠标进行拖拽,让元素跟随鼠标进行移动,鼠标抬起,元素停止移动。 解析: 鼠标按下事件:onmousedown 鼠标移动事件:onmousemove 鼠标抬起事件:onmouseup <!DOCT…...

第十二章 项目采购管理
12.1 规划采购管理 12.2 实施采购 12.3 控制采购 项目经理通常没有签订合同的权限,但必须熟悉正规的采购流程; 协议是采购的核心文件,关于协议我们要知道: 协议包括:合同、服务水平协议、谅解、协议备忘录或采购订单 ❗…...

PSFR-GAN复现
写在前面:本博客仅作记录学习之用,部分图片来自网络,如需引用请注明出处,同时如有侵犯您的权益,请联系删除! 文章目录 前言快速开始安装依赖权重下载及复原 训练网络数据集训练脚本 代码详解训练BaseOptio…...

函数和数组
一、函数 1.函数使用方法 定义函数再引用函数 2.基本函数格式 基本格式1: function 函数名{ 命令序列 } 基本格式2: 函数名(){ 命令序列 } 基本格式3: function func_name () {…...
docker安装时报错:Error: Nothing to do
安装docker时报以下错误 解决方法: 1.下载关于docker的相关依赖环境 yum -y install yum-utils device-mapper-persistent-data lvm22.设置下载Docker的镜像源 yum-config-manager --add-repo http://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo3…...

白盒测试:覆盖测试及测试用例设计
白盒测试:覆盖测试及测试用例设计 一、实验目的 1、掌握白盒测试的概念。 2、掌握逻辑覆盖法。 二、实验任务 某工资计算程序功能如下:若雇员月工作小时超过40小时,则超过部分按原小时工资的1.5倍的加班工资来计算。若雇员月工作小时超过…...

Java高级开发2024高频面试提问题目
1、请先简单自我介绍一下自己?(一般不超过5min) 2、你最熟悉的项目是哪一个,讲一下用了哪些技术栈?(尽量讲出系统架构图使用到的技术组件和为什么选型这个组件?) 3、你项目中使用什…...

Kamailio openssl 3.0.x 需要注意的事项
我们留意到 Debian Bookworm 安装的 openssl 版本是 3.0.x 这里有几个地方要注意: modparam("tls", "init_mode", 1)核心参数 tls_threads_mode 配置为 1 或者 配置为 2,默认为 0版本建议用 5.8.1,貌似 5.7.x 也行 参…...
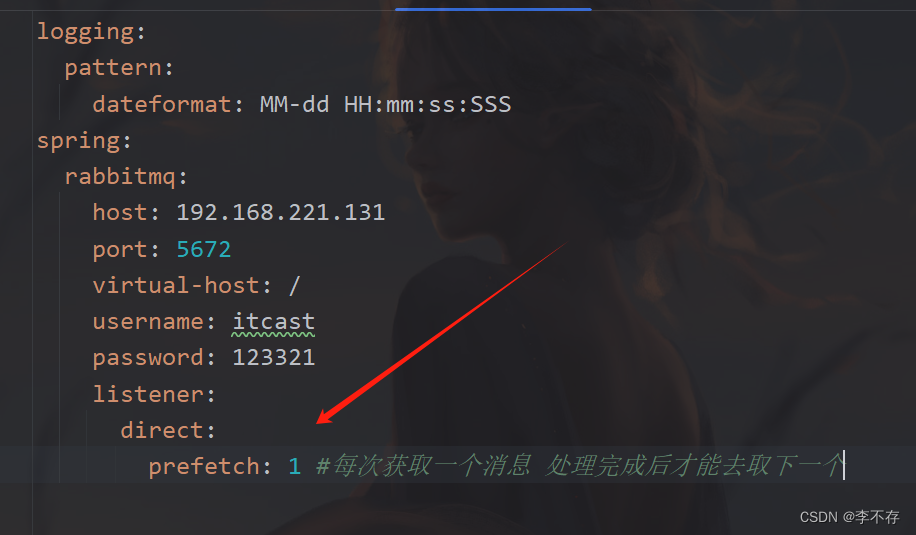
SpringAMQP Work Queue 工作队列
消息模型: 代码模拟: 相较于之前的基础队列,该队列新增了消费者 不再是一个,所以我们通过代码模拟出两个consumer消费者。在原来的消费者类里写两个方法 其中消费者1效率高 消费者2效率低 RabbitListener(queues "simple.queue")public voi…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...
