每日一练-等差数列
等差数列
- 🍀题目描述
- 🌿解题思路
- 🌸Python源码
- 📧Summary
📆Date: 2023年2月10日
🎬Author: 小 y 同 学
📃Classify: 蓝桥杯每日一练
🔖Language: Python
🍀题目描述
题意
数学老师给小明出了一道等差数列求和的题目。但是粗心的小明忘记了一部分的数列,只记得其中 N 个整数。
现在给出这 N 个整数,小明想知道包含这 N 个整数的最短的等差数列有几项?输入格式
输入的第一行包含一个整数 N。
第二行包含 N 个整数 A1, A2, · · · , AN。(注意 A1 ∼ AN 并不一定是按等差数列中的顺序给出)输出格式
输出一个整数表示答案。样例输入
5 2 6 4 10 20
- 样例输出
10
样例说明
包含 2、6、4、10、20 的最短的等差数列是 2、4、6、8、10、12、14、16、18、20。评测用例规模与约定
对于所有评测用例,2 ≤ N ≤ 100000,0 ≤ Ai ≤ 109。
🌿解题思路
- 题目梳理
题目会给出一串数字,我们需要做的就是找出包含这些数字的等差数列,且这个等差数列的项数最小,注意我们要输出的是等差数列的项数,不是等差数列的元素或者其求和。- 核心处理
首先给出的数字串是没有顺序的,我们首先肯定是想到将给出的数字排序。然后我们要做的就是寻找公差:起初小y想的是排序完的数组每相邻两项做差,然后最小的就是公差,但是仔细一想:如果排序完的数组中的相邻两项差一个是2,一个是3:例如数组:1、3、6;要想组成等差数列,必须以1为公差;随后就想到了取2和3的最大公因数也就是1来作为公差;同样的思路,就可以类比出给出的任意数列对应的公差。随后就是求项数,给出的数列最小的和最大的一定是等差数列的首尾项,我们可以由an=a1+(n−1)×da_n=a_1+(n-1)\times dan=a1+(n−1)×d推导出n=an−a1d+1n=\frac{a_n - a_1}{d}+1n=dan−a1+1,但是我们要注意d为0的情况分开讨论!
🌸Python源码
# _*_coding:utf-8_*_ # created by cy on 2023/2/10 import math# 求最大公因数 def gcd_many(li, n): g = 0 for i in range(n):if i == 0:g = li[i]else:g = math.gcd(g, li[i]) return gn = int(input()) A = list(map(int, input().split())) A.sort() d_li = [] for i in range(n - 1): d_li.append(A[i + 1] - A[i]) if min(d_li) == 0: # 公差为0的情况 print(n) else: d = gcd_many(A, n) print(int((A[-1] - A[0]) / d + 1))
📧Summary
小y的今日一练到此画上了句号,欢迎友友们多给建议🌼🌼🌼
有兴趣一起学习编程的小伙伴可以私聊小y一起学习,小y在Python,c/c++和matlab语言上均有一定的基础😜😜😜
相关文章:

每日一练-等差数列
等差数列🍀题目描述🌿解题思路🌸Python源码📧Summary📆Date: 2023年2月10日 🎬Author: 小 y 同 学 📃Classify: 蓝桥杯每日一练 🔖Language: Python 🍀题目描述 题意 …...
使用动态参数构建CUDA图
文章目录使用动态参数构建CUDA图使用显式 API 调用构建 CUDA 图使用流捕获构建 CUDA 图组合方法执行结果总结使用动态参数构建CUDA图 自从在 CUDA 10 以来,CUDA Graphs 已被用于各种应用程序。 上图将一组 CUDA 内核和其他 CUDA 操作组合在一起,并使用指…...

在Fortran中调用Python教程
前言Python是机器学习领域不断增长的通用语言。拥有一些非常棒的工具包,比如scikit-learn,tensorflow和pytorch。气候模式通常是使用Fortran实现的。那么我们应该将基于Python的机器学习迁移到Fortran模型中吗?数据科学领域可能会利用HTTP AP…...
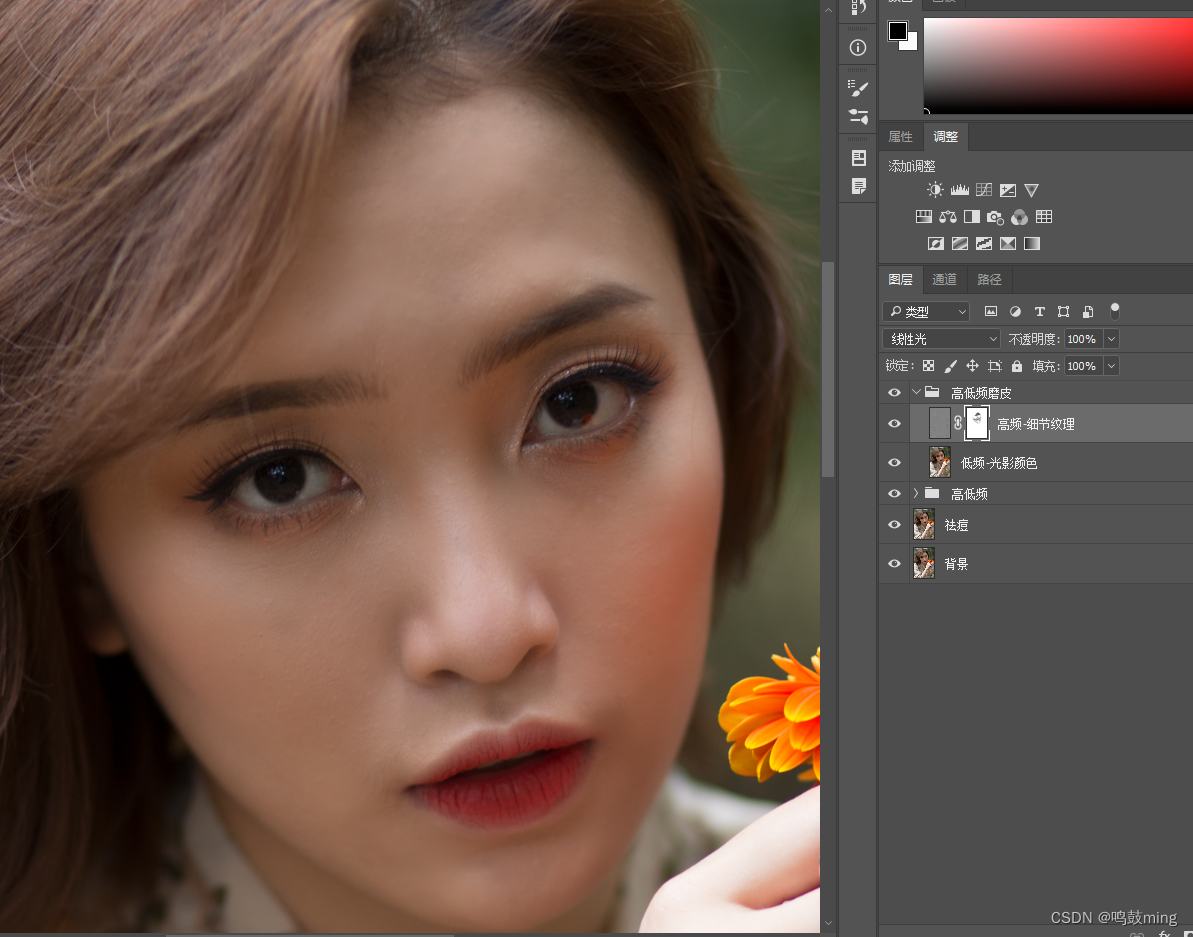
04-PS人像磨皮方法
1.高斯模糊磨皮 这种方法的原理就是建立一个将原图高斯模糊后图层, 然后用蒙版加画笔或者历史画笔工具将需要磨皮的地方涂抹出来, 通过图层透明度, 画笔流量等参数来控制磨皮程度 1.新建图层(命名为了高斯模糊磨皮), 混合模式设置为正常, 然后选择高斯模糊, 模糊数值设置到看…...
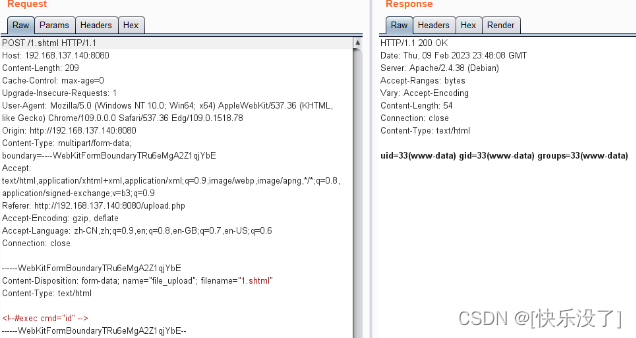
nginx反向代理+负载均衡上传webshell重难点+apache漏洞
nginx反向代理 nginx 负载均衡 负载均衡的策略 1、轮询:nginx默认就是轮询其权重都默认为1,服务器处理请求的顺序:ABABABABAB… upstream mysvr { server 192.168.137.131; server 192.168.137.136; }2、weight:跟据配置…...

transition组件的使用
<template><button click"flag !flag">切换</button><transition name"fade"><div v-if"flag" class"box"></div></transition> </template><script setup lang"ts"&g…...
多行文本在块元素中垂直居中
单行文本垂直居中对齐 在块元素中,让单行文本居中,可以使用line-height等于块元素的高,即可让该单行文本垂直居中对齐。 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><me…...

在 WebAssembly 中使用 C/C++ 和 libbpf 编写 eBPF 程序
作者:于桐,郑昱笙 eBPF(extended Berkeley Packet Filter)是一种高性能的内核虚拟机,可以运行在内核空间中,用来收集系统和网络信息。随着计算机技术的不断发展,eBPF 的功能日益强大,…...

leveldb源码解析六——compact
compact分为manual_compaction、minor_compaction、major_compaction,统一由MaybeScheduleCompaction触发: void DBImpl::MaybeScheduleCompaction() {mutex_.AssertHeld();if (background_compaction_scheduled_) {// Already scheduled} else if (shu…...

数据结构(二):单向链表、双向链表
数据结构(二)一、什么是链表1.数组的缺点2.链表的优点3.链表的缺点4.链表和数组的区别二、封装单向链表1. append方法:向尾部插入节点2. toString方法:链表元素转字符串3. insert方法:在任意位置插入数据4.get获取某个…...

COCO物体检测评测方法简介
本文从ap计算到map计算,最后到coco[0.5:0.95:0.05] map的计算,一步一步拆解物体检测指标map的计算方式。 一、ap计算方法 一个数据集有多个类别,对于该数据库有5个gt,算法检测出来10个bbox,对于人这个类别来说检测有…...

记一次上环境获取资源失败的案例
代码结构以及资源位置 测试代码 RestController RequestMapping("/json") public class JsonController {GetMapping("/user/1")public String queryUserInfo() throws Exception {// 如果使用全路径, 必须使用/开头String path JsonController.class.ge…...

实战超详细MySQL8离线安装
在RedHat中,RPM Bundle 方式安装MySQL8。建议一定要用 RPM Bndle 版本安装,包全。官网下载:https://dev.mysql.com/downloads/mysql/1.卸载mariadb,会与MySQL安装冲突。rpm -qa | grep mariadb 查看有无mariadb如果有࿰…...

依赖倒置原则|SOLID as a rock
文章目录 意图动机:违反依赖倒置原则解决方案:C++中依赖倒置原则的例子依赖倒置原则的优点1、可复用性2、可维护性在C++中用好DIP的标准总结本文是关于 SOLID as Rock 设计原则系列的五部分中的 最后一部分。 SOLID 设计原则侧重于开发 易于维护、可重用和可扩展的软件。 在…...
Webpack的知识要点
在前端开发中,一般情况下都使用 npm 和 webpack。 npm是一个非常流行的包管理工具,帮助开发者管理项目中使用的依赖库和工具。它可以方便地为项目安装第三方库,并在项目开发过程中进行版本控制。 webpack是一个模块打包工具ÿ…...
handler解析(2) -Handler源码解析
目录 基础了解: 相关概念解释 整体流程图: 源码解析 Looper 总结: sendMessage 总结: ThreadLocal 基础了解: Handler是一套 Android 消息传递机制,主要用于线程间通信。实际上handler其实就是主线程在起了一…...

【算法】kmp
KMP算法 名称由来 是由发明这个算法的三个科学家的名称首字母组成 作用 用于字符串的匹配问题 举例说明 字符串 aabaabaaf 模式串 aabaaf 传统匹配方法 第一步 aabaabaaf aabaaf 此时,b和f不一致,则把模式串从头和文本串的第二个字符开始比 第…...
git 常用命令之 git checkout
大家好,我是 17。 git checkout 是 git 中最重要最常用的命令之一,本文为大家详细解说一下。 恢复工作区 checkout 的用途之一是恢复工作区。 git checkout . checkout . 表示恢复工作区的所有更改,未跟踪的文件不会有变化。 恢复工作区的所有文件风…...
一些常见错误
500状态码: 代表服务器业务代码出错, 也就是执行controller里面的某个方法的过程中报错, 此时在IDEA的控制台中会显示具体的错误信息, 所以需要去看IDEA控制台的报错404状态码: 找不到资源找不到静态资源 检查请求地址是否拼写错误 检查静态资源的位置是否正确 如果以上都没有问…...
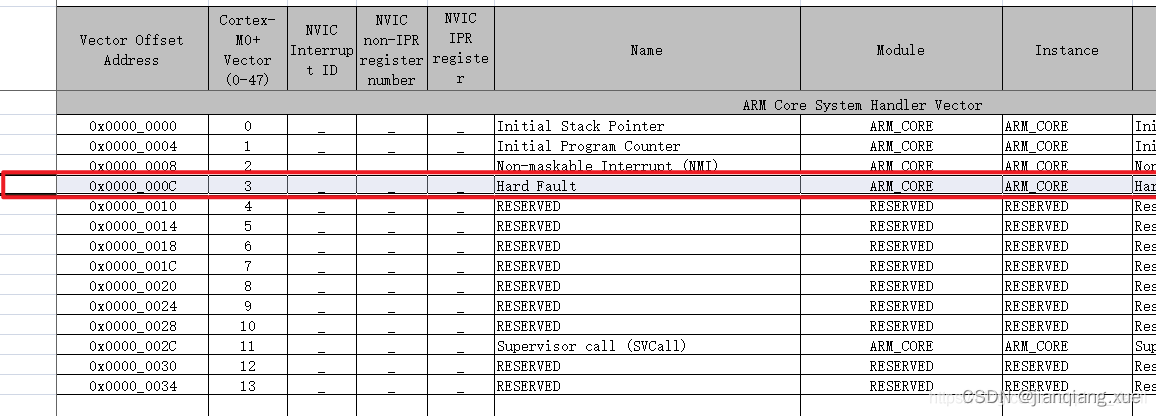
[单片机框架][调试功能] 回溯案发现场
程序莫名死机跑飞,不知道问题,那么下面教你回溯错误源 回溯案发现场一、修改HardFault_Handler1. xx.s 在启动文件,找到HardFault_Handler。并修改。2. 定义HardFault_Handler_C函数。(主要是打印信息并存储Flash)3. 根…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...
