【机器学习】逻辑化讲清PCA主成分分析
碎碎念:小编去年数学建模比赛的时候真的理解不了主成分分析中的“主成分”的概念!!但是,时隔两年,在机器学习领域我又行了,终于搞明白了!且看正文!再分享一个今天听到的播客中非常触动我的一句话吧:“人生也许没有诗和远方,你脚下的苟且就是你没有发现的诗和远方。”来自钱婧老师的新书《我有自己的宇宙》
第一次更新:2024/5/10
目录
一. 引入
1. 为什么要降维
2. 如何降维
二. PCA(Principal Component Analysis)主成分分析
1. 主要思想
1.1 相关性理解
1.2 特征空间重构
1.3 主成分
2. 数学建模
2.1 最大投影方差
2.2 最小重构代价
3. 算法原理
4. matlab代码
一. 引入
1. 为什么要降维
数据的维度增高在机器学习中会带来“维度灾难”:高维度数据(如大型矩阵或稠密向量)可能会占用大量存储空间,并且计算复杂性和时间可能会随着维度的增加而急剧增加。这可能导致计算资源和存储空间的瓶颈,从而影响算法性能和系统效率。同时,高维数据也会带来数据稀疏,怎么理解这个稀疏呢?
假设我们有一个全世界总人口的数据集,如果我们按照性别这个特征关注数据,会发现此时数据是稠密并且相对均匀分布的;如果我们加入年龄、学历又会发现,此时的数据相对原来有一点点稀疏;如果再加入性格、身高、外貌等多个维度的特征时会发现满足这些特征的数据只有你一个,这个维度下的数据当然是稀疏的。
所以为了提高我们处理数据的模型的性能,降低计算的复杂度我们就会用到“降维”这个手段了。
2. 如何降维
我们常见的降维手段主要包括三类:特征降维、线性降维、非线性降维。
- 特征降维主要思想就是人为或者机器来筛选我们需要的特征,将不需要的特征变量删除;
- 线性降维是最常用的降维手段,主要包括PCA主成分降维和多维缩放降维;
- 非线性降维主要思想是主要思想是利用非线性映射将原始数据从原始空间映射到一个低维空间,主要包括IsoMAP、LLE算法等。
二. PCA(Principal Component Analysis)主成分分析
1. 主要思想
先来搜一下常见定义:
主成分分析(PCA:Principal Component Analysis)旨在通过正交变换将可能存在相关性的变量转换为一组线性不相关的变量,即主成分。PCA的核心是数据降维思想,通过降维手段实现多指标向综合指标的转化,使得转化后的综合指标(主成分)之间互不相关,并且尽可能地保留原始数据集的信息。
但看这一段是不是很懵?我也很懵,咱别看它,开始我们的正文。
我们知道一个数据集的如果特征较多的话就可能导致某些特征之间是存在相关性的,降维的一个切入点就可以是尽量让可以代表一类特征的一个变量来代替很多变量,进一步可以设想达到我们降维后的变量之间的相关性非常小,这样就说明我们降维后的变量是“有代表性的”。在数学中如何刻画这种相关性呢?我们分为几何角度和代数角度:
1.1 相关性理解
几何角度
我们先来看一个二维特征空间:
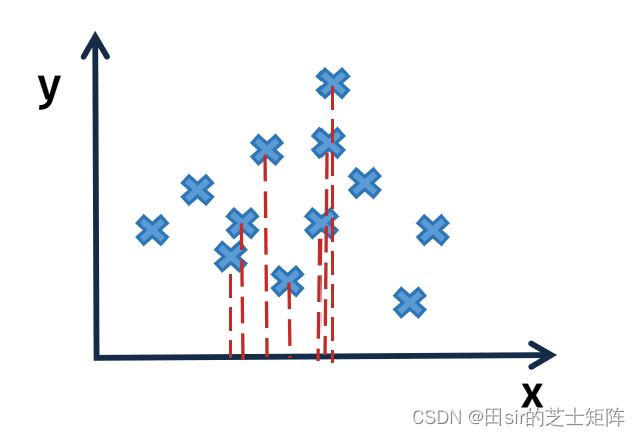
我们发现在x轴上数据呈现出明显的“拥挤”现象,即特征变量的相关性较高在几何上通常表现为线条的聚集或重叠。这意味着多个特征变量在图形上表现出较为接近的分布,它们的线条有时会交叉或重叠。这表明这些变量之间存在较高的相关关系,即一个变量的变化往往伴随着另一个变量的相应变化。
代数角度
数据在某一方向上的“拥挤”在数学上可以理解为在这个方向上数据的波动性较小(总体方差较小)。当特征变量之间高度相关时,在数据集中不同的特征变量波动方向和大小通常相近,因此总体方差相对较小。
同时高度相关的特征变量之间可能存在多重共线性问题,即它们之间存在相互依赖的关系。这可能导致方差解释性的降低,因为多重共线性的存在可能会混淆变量之间的因果关系。
1.2 特征空间重构
我们在原有的方向上特征重合度较高,主成分分析给予我们一个思路:换个角度看
如果旋转一下坐标系,使得在新坐标系下不同特征“分得很开”,会更有利于我们理解数据:

当我们在新的坐标系再观察数据时会发现,从
的方向上看数据已经相对不再那么“拥挤”了,此时数据在
方向上的离散程度最大,即方差最大。
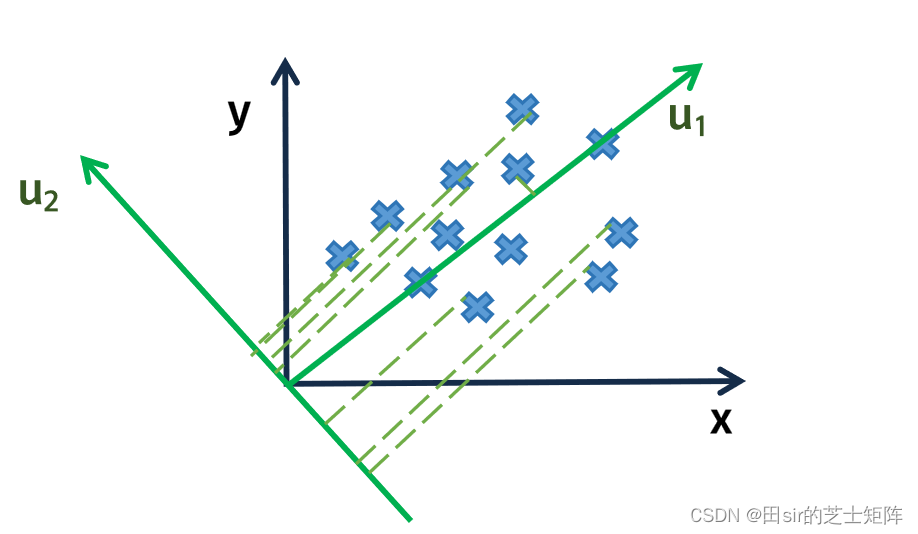
与此同时在轴上的方差较小。
所构建的新的特征空间简化了系统结构。
1.3 主成分
在主成分分析中,主成分指的是数据方差最大的方向,即数据在某一方向上的变化。
在我们的二维例子中,方向的方差最大,也就是第一主成分;其次,
为第二主成分。
在高维坐标系下我们做的工作也只是构建一个特征空间,按照每个坐标轴(也就是该特征空间下的基)方向的方差大小排序,就可以得到第一、第二、第三...主成分了。
通过将原始数据投影到主成分的坐标系中,我们可以减少数据的维度,同时保留原始数据中的大部分信息。主成分分析的目标是找到数据的主成分,这些主成分能够最大限度地保留原始数据的方差,同时尽可能减少彼此之间的相关性。
在主成分分析中,第一个主成分通常包含原始数据集中的大部分信息,因为它对应于数据的主要变化方向。后续的主成分通常包含的数据信息逐渐减少,因为它们更多地反映原始数据中的冗余或重复信息。
2. 数学建模
主成分分析的核心数学原理借鉴b站博主的又红又专的总结:一个中心,两个基本点
- 一个中心:对原始特征空间的重构,将相关特征转化为无关特征
- 两个基本点:(1)最大投影方差 (2)最小重构代价
机器学习-白板推导系列(五)-降维(Dimensionality Reduction)_哔哩哔哩_bilibili
在主要思想板块我们详细讲了特征空间的重构,这里就不过多赘述了,下面我们来手推两个基本点
2.1 最大投影方差
前提:
数据中心化:
向量长度: 即

数学模型:
结论:
主成分方向就是特征值λ的最大特征向量方向
2.2 最小重构代价

数学模型:
结论:
前q个主成分最大的方向就是协方差阵的前q个特征向量
3. 算法原理
基本的算法思路如下:
- 数据标准化:在PCA之前,所有数据都应该标准化(归一化)。这是由于PCA通过线性变换对特征进行降维,所以任何具有非零均值的特征都可能被误导。
- 计算协方差矩阵:PCA基于协方差矩阵对数据进行降维。在这个过程中,我们假设所有变量之间都存在某种相关性。
- 计算协方差矩阵的特征向量和特征值:协方差矩阵的特征向量表示了数据的主要变化方向,而特征值的平方根表示了每个方向上的方差贡献。
- 选择主成分:选择前k个主成分,其中k是我们要降到的维度数。通常会选择那些特征值占总特征值之和的95%以上的主成分。
- 应用主成分:对于原始数据中的每个样本,我们可以通过将其投影到选定的主成分上,从而将其降维到新的维度数。
4. matlab代码
function [tg xs q px newdt]=pca(h)
%数据标准化
h=zscore(h); %计算相关系数矩阵
r=corrcoef(h);
disp('计算的相关系数矩阵如下:');
disp(r)%计算特征向量与特征值
[x,y,z]=pcacov(r);
s=zeros(size(z));%创建0矩阵
for i=1:length(z)s(i)=sum(z(1:i));
end%主成分贡献率计算
disp('前几个特征根及其贡献率:');
disp([z,s])
tg=[z,s];
f=repmat(sign(sum(x)),size(x,1),1);
x=x.*f;%主成分选择
n=input('请选择前n个需要计算的主成分:\n');
disp('由此可得选择的主成分系数分别为:');
for i=1:nxs(i,:)=(x(:,i)');
end
newdt=h*xs';
disp('以主成分的贡献率为权重,构建主成分综合评价模型系数:');
q=((z(1:n)./100)')
w=input('是否需要进行主成分综合评价?(y or n)\n');
if w==ydf=h*x(:,1:n);tf=df*z(1:n)/100;[stf,ind]=sort(tf,'descend'); %按照降序排列disp('主成分综合评价结果排序:');px=[ind,stf]
elsereturn;
end相关文章:
【机器学习】逻辑化讲清PCA主成分分析
碎碎念:小编去年数学建模比赛的时候真的理解不了主成分分析中的“主成分”的概念!!但是,时隔两年,在机器学习领域我又行了,终于搞明白了!且看正文!再分享一个今天听到的播客中非常触…...

Vue常见的指令
Vue.js 提供了许多内置指令,这些指令可以在模板中用于处理元素的显示、行为等。以下是 Vue.js 中常见的 7 个指令及其详细代码示例: 1、v-bind:用于属性绑定,可以动态更新 HTML 属性。 html<template> <div> <img…...
【Ansible】ansible-playbook剧本
playbook 是ansible的脚本 playbook的组成 1)Tasks:任务;通过tasks 调用ansible 的模板将多个操作组织在一个playbook中运行 2)Variables:变量 3)Templates:模板 4)Handles…...
Linux的命令
; 昨天学习了七个命令,分别是:cd命令(切换目录)、pwd命令(当前目录)、mkdir命令(创建目录)、touch命令(创建文件)、date命令(显…...

No known conditions for “./lib/locale/lang/zh-cn“ entry in “element-plus“ pa
yarn的安装和卸载 npm install -g yarn npm uninstall yarn -g //yarn卸载 改用yarn卸载试试 先安装yarn npm install -g yarn 卸载掉原来的element-plus yarn remove element-plus 重新安装原有的element-plus版本 yarn add element-plus2.3.1 低版本页面引用为 i…...
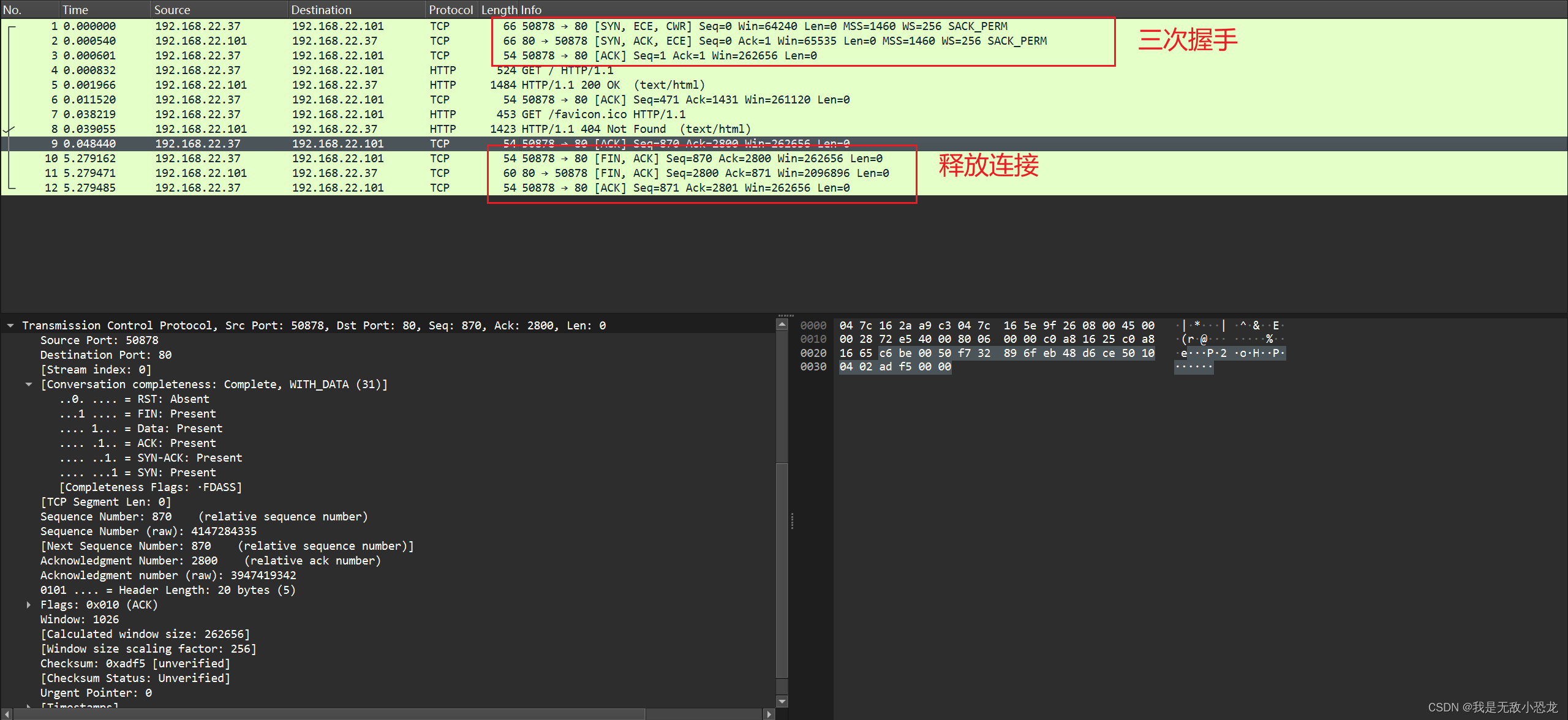
实验名称:TCP 连接管理
目录 前言 TCP报文段格式 TCP建立连接 TCP释放连接 实验目的 实验原理 实验步骤 1. 启动WireShark,设置抓包状态 2. 访问指定服务器 ,通过Wireshark抓取通信数据报文 3. 分析TCP连接建立的三次握手和连接释放的四次握手过程 原始数据记录 实验…...
)
go语言map底层及扩容机制原理详解(上)
底层数据结构-哈希表 go语言map的底层数据结构是哈希表:通过哈希表来存储键值对,通过hash函数把键值对散列到一个个桶(bucket)中。 什么是哈希表? 在顺序结构以及平衡树中,元素与其的存储位置之间没有对应关系,因此…...

互联网职场说 | “领导找我谈话,原来是给我涨薪,但却只涨了200,还偷偷叮嘱我保密,这次只给我涨了薪”
职场中,一般当领导找你谈话时,心里总是会涌起两种心理活动:问责和表扬。不过很多人第一反应就是有点担心害怕,其次才会想有什么好事临到我了! 一位职场网友分享说,有天领导忽然找她谈话,当时心…...

Android 如何启用user版本的adb源码分析
Android调试桥(ADB, Android Debug Bridge)是一个Android命令行工具,包含在SDK 平台工具包中,adb可以用于连接Android设备,或者模拟器,实现对设备的控制,比如安装和调试应用。和Appium一样,adb也是基于C/S架…...
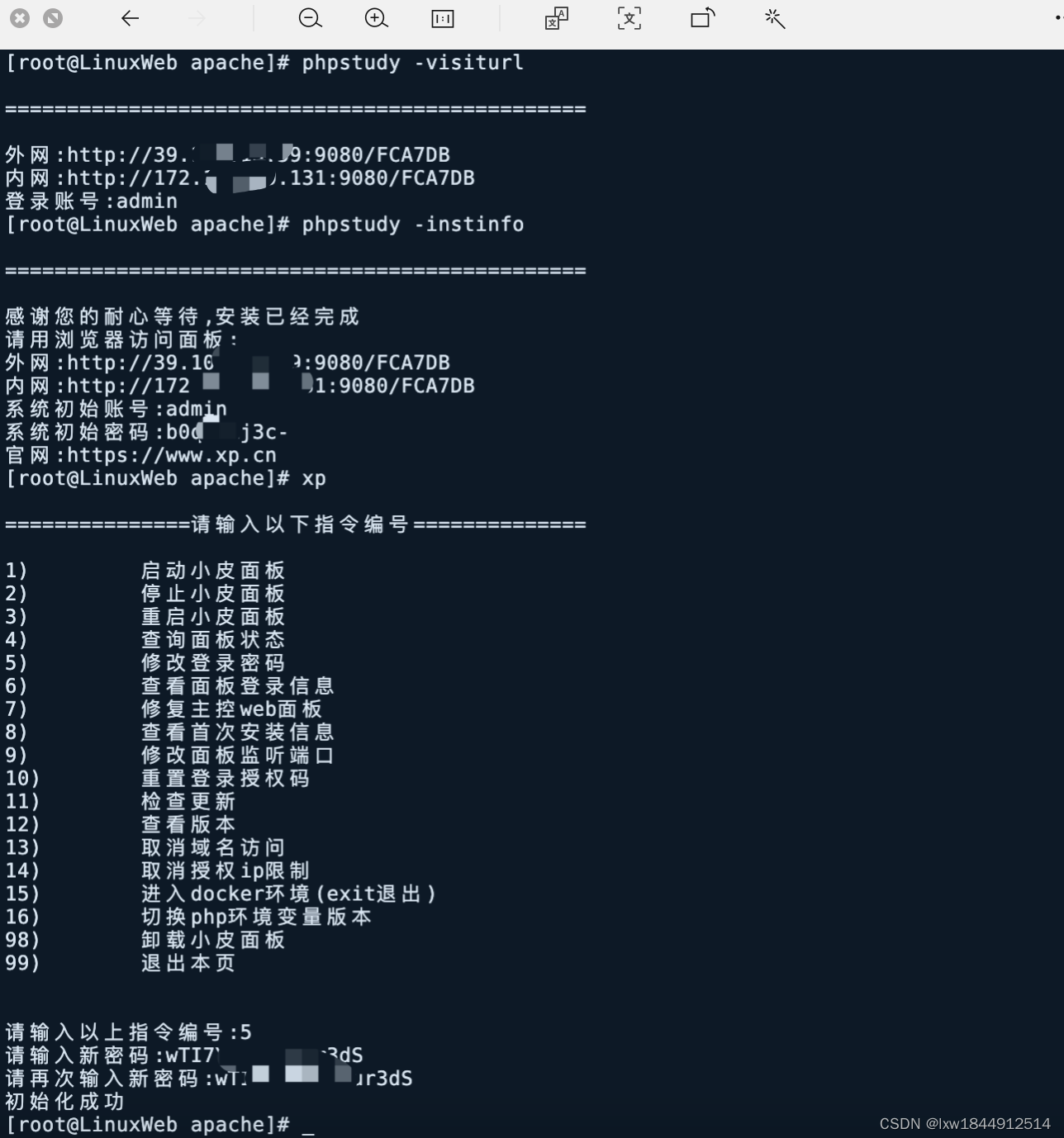
linux phpstudy 重启命令
[rootLinuxWeb phpstudy]# ./system/phpstudyctl restart 查看命令 1) phpstudy -start 启动小皮面板 2) phpstudy -stop 停止小皮面板 3) phpstudy -restart 重启小皮面板 4) phpstudy -status 查询面板状态 5) phpstudy -in…...
台式电脑屏幕亮度怎么调节?让你的眼睛更舒适!
在日常使用台式电脑时,调节屏幕亮度是一项常见的需求。不同的环境和个人偏好可能需要不同的亮度设置。因此,了解台式电脑屏幕亮度怎么调节是非常重要的。本文将介绍三种常见的方法,帮助您轻松调节台式电脑屏幕亮度,以满足您的需求…...

打造安全的 Linux 环境:实用配置指南
唠唠闲话 一开始接触服务器,我只是把它当博客的托管网站,源文件用 GitHub 备份,所以网站被黑了也没啥关系。但随着使用深入,网站逐渐加入我的日常工作流中,而且有了使用更多服务的需求。在这种情况下,服务…...

神经网络有哪些算法
神经网络算法是人工智能领域的重要组成部分,它通过模拟人类神经系统的结构和功能,实现对复杂问题的处理和分析。以下是对神经网络算法的详细概述,包括常见的算法和它们的特点、应用等,力求达到约2500字的篇幅。 一、神经网络算法概述 神经网络算法是一种基于人工神经元的…...

计算机网络期末试题
第一章 概述 一. 单选题(共13题,36.4分) 1. (单选题) 因特网起源于( )网络。 A. ARPANETB. EthernetC. CATVD. CERNET 我的答案: A:ARPANET;正确答案: A:ARPANET; 2.8分 2. (单选题)人们把( )年作为因特网的诞…...

Unity学习笔记---图层
渲染层级 1,调整Sprite Renderer中的Order in Layer可以调整图层层级。 2,在Edit--Project Setting--Graphics中,调整TransParency Sort Mode为Custom Axis, 并将TransParency Sort Axis中的Z值默认的1改为0,将Y改为…...

【简单探索微软Edge】
🎥博主:程序员不想YY啊 💫CSDN优质创作者,CSDN实力新星,CSDN博客专家 🤗点赞🎈收藏⭐再看💫养成习惯 ✨希望本文对您有所裨益,如有不足之处,欢迎在评论区提出…...

YOLOv5独家改进:backbone改进 | 微软新作StarNet:超强轻量级Backbone | CVPR 2024
💡💡💡创新点:star operation(元素乘法)在无需加宽网络下,将输入映射到高维非线性特征空间的能力,这就是StarNet的核心创新,在紧凑的网络结构和较低的能耗下展示了令人印象深刻的性能和低延迟 💡💡💡如何跟YOLOv5结合:替代YOLOv5的backbone 收录 YOL…...

概率密度函数pdf的某种解释与洞察
1.一个想法实验 我在想一个数,姑且称之为X,介于0和10之间(含0和10)。如果我不告诉你别的,你会想象X = 0的概率是多少?X = 4?假设我对任何特定的数字都没有偏好,你会想象十一个整数0,1,2,.….,10也是一样。因为所有的概率加起来必须是1,所以逻辑上的结论是给11个选项…...
)
【OceanBase诊断调优】—— 转储错误(错误代码 4138/ORA-01555)
当读事务很长时,租户进行转储会报 4138/ORA-01555 错误。本文介绍该错误的处理方法。 适用版本 OceanBase 数据库 V2.X 及以后的版本 问题现象 当读事务很长,租户进行转储时会出现以下错误。 Oracle 租户: ORA-01555:snapsho…...

Python面试题【数据结构和算法部分101-130】
Python面试题【数据结构和算法部分101-130】 Python面试题【数据结构和算法部分101-130】 Python面试题【数据结构和算法部分101-130】 问题:如何在Python中实现二分查找? 答案: def binary_search(arr, target):low, high 0, len(arr) - 1…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...
