爬虫应该选择住宅ip代理还是数据中心代理?
住宅代理
住宅代理是互联网服务提供商 (ISP) 提供的 IP 地址,它们是附加到实际物理位置的真实IP地址。住宅代理允许用户通过目标区域内的真实IP地址连接到互联网。
数据中心代理
数据中心代理是指是使用数据中心拥有并管理IP的代理,IP地址来源于数据中心机房,不需要其他设备再进行路由。这可以让数据中心更好地直接控制速度并保障安全性。
爬虫应该选择住宅ip代理还是数据中心代理?
选择代理ip,首先肯定要根据自身的业务场景来决定,自身业务与代理ip是否符合需求。下面小编就再来给大家介绍一下它们俩的一些对比
1、安全性
安全性分为很多方面,我们以匿名性来分析。住宅ip代理和数据中心代理都有一定程度的匿名性。但数据中心ip时连号的,就是使用的时候上一个ip和下一个ip时连号的,对于目标站点更容易识别。住宅ip因为是真实的家庭ip地址,所以更加真实安全。
2、代理速度
因为设备的原因,数据中心代理是在中心机房中,设备是比较完善的;而住宅ip就相当于家庭设备。所以在速度上数据中心代理是高于住宅ip代理的。
3、价格
价格上数据中心因其设备的完善更高,配置也就越高,所以在价格上数据中心代理要高于住宅ip代理。
总结:如果需要再业务执行的效率上快的话,就选择数据中心代理。如果需要安全性高的话,更加真实,且价格要求低,就选择住宅ip代理。
以上就是爬虫应该选择住宅ip代理还是数据中心代理,希望对大家有所帮助!
相关文章:

爬虫应该选择住宅ip代理还是数据中心代理?
住宅代理 住宅代理是互联网服务提供商 (ISP) 提供的 IP 地址,它们是附加到实际物理位置的真实IP地址。住宅代理允许用户通过目标区域内的真实IP地址连接到互联网。 数据中心代理 数据中心代理是指是使用数据中心拥有并管理IP的代理,IP地址来源于数据中…...

百面算法工程师目录 | 深度学习目标检测、语义分割、分类上百种面试问答技巧
本文给大家带来的百面算法工程师是深度学习面试目录大纲,文章内总结了常见的提问问题,旨在为广大学子模拟出更贴合实际的面试问答场景。在这篇文章中,可以点击题目直达问题答案处,方便查找问题寻找答案。节约大家的时间。通过对这…...
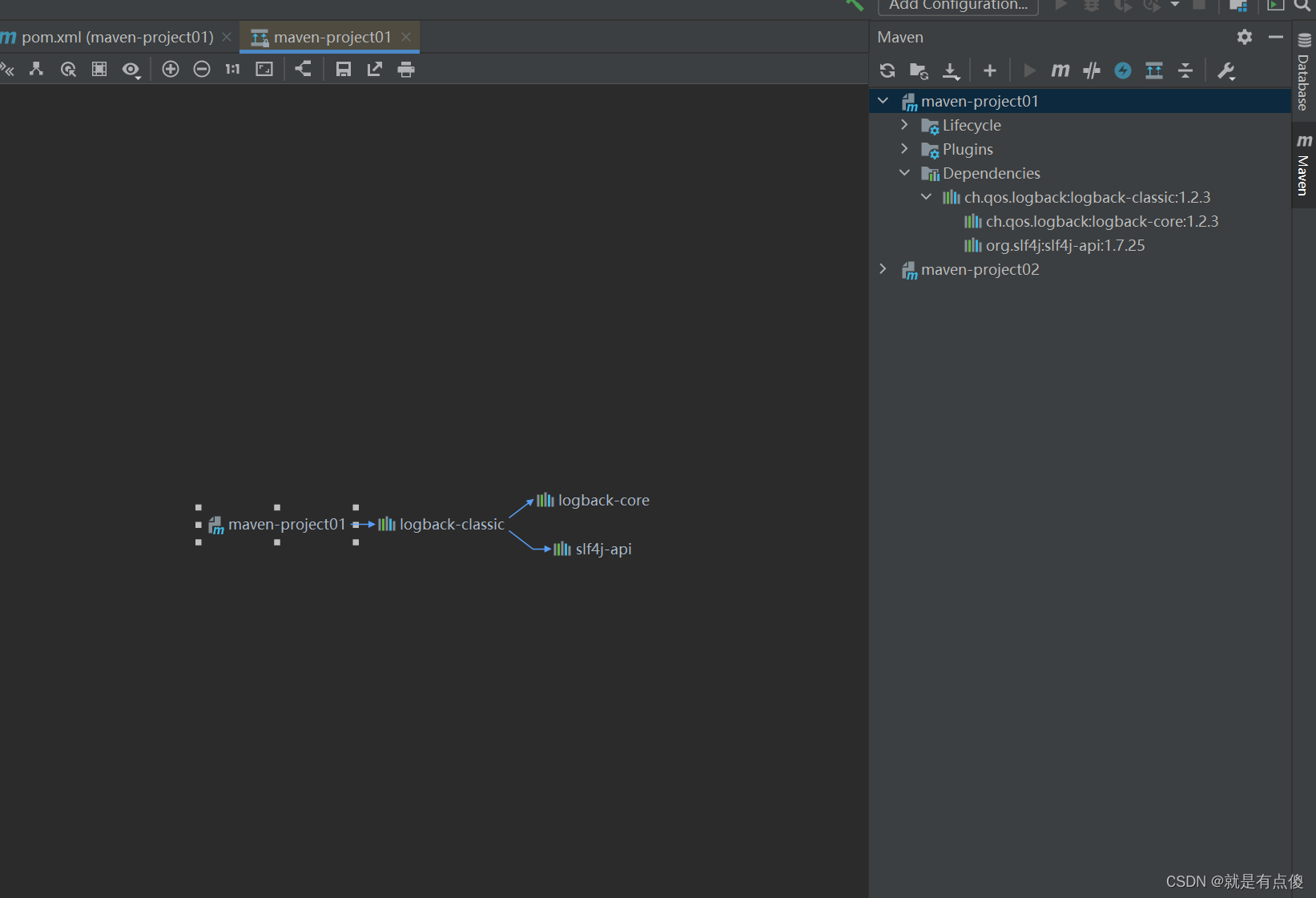
Java中Maven的依赖管理
依赖介绍 是指当前项目运行所需要的jar包,一个项目中可以引入多个依赖 配置 在pom.xml中编写<dependencies>标签 在<dependencies>中使用<dependency>引入标签 定义坐标的groupId、rtifactId、version 点击刷新按钮、引入新坐标 例如引入下…...
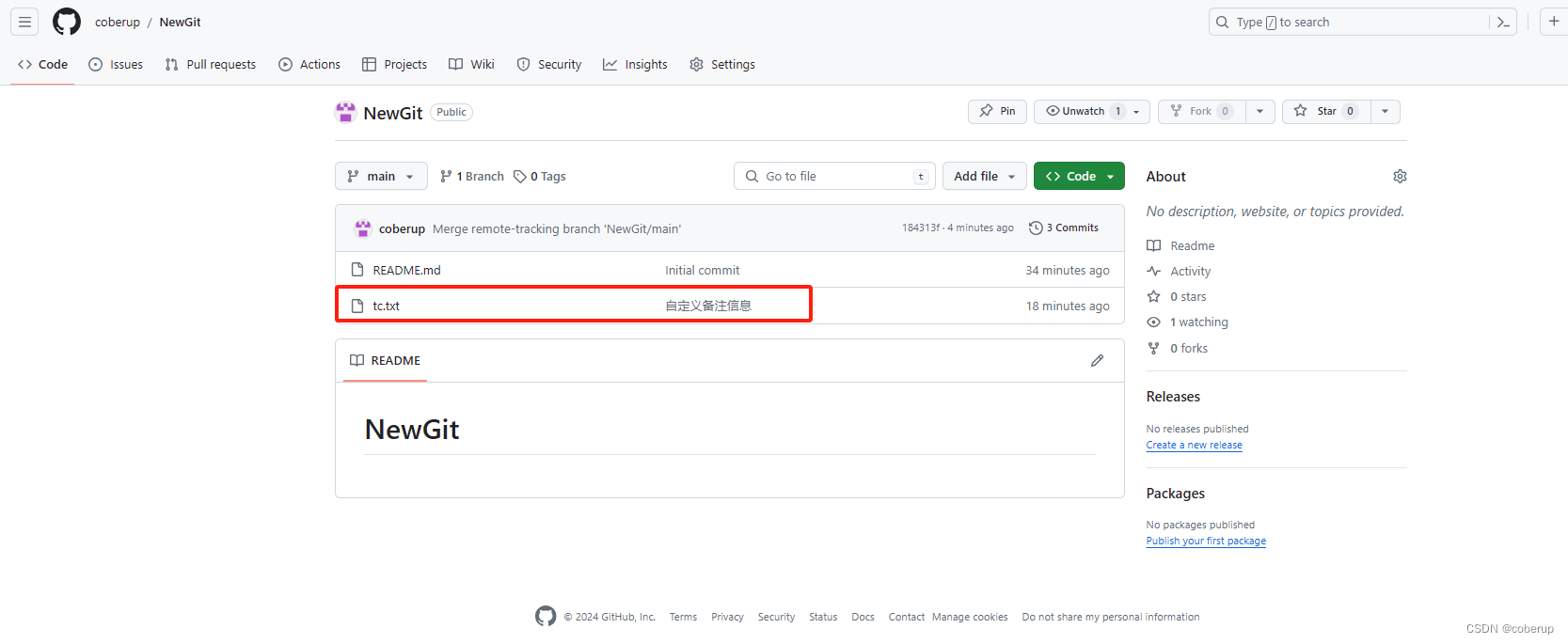
Github新手入门使用方法
**存在问题:**新手如何快速入门github,能够下载开源文件,并且修改后更新远程github仓库; 解决方案: 参考: http://www.360doc.com/content/24/0301/12/60419_1115656653.shtml https://blog.csdn.net/gongd…...
期权隐含波动率到底是什么意思?
今天期权懂带你了解期权隐含波动率到底是什么意思?期权隐含波动率解析。通俗的说,期权隐含波动率是在期权市场中买家和卖家对于,某一期权合约价格变动幅度大小的判断。 期权隐含波动率到底是什么意思? 隐含波动率是根据期权市场价…...

28、Flink 为管理状态自定义序列化
为管理状态自定义序列化 a)概述 对状态使用自定义序列化,包含如何提供自定义状态序列化程序、实现允许状态模式演变的序列化程序。 b)使用自定义状态序列化程序 注册托管 operator 或 keyed 状态时,需要 StateDescriptor 来指…...
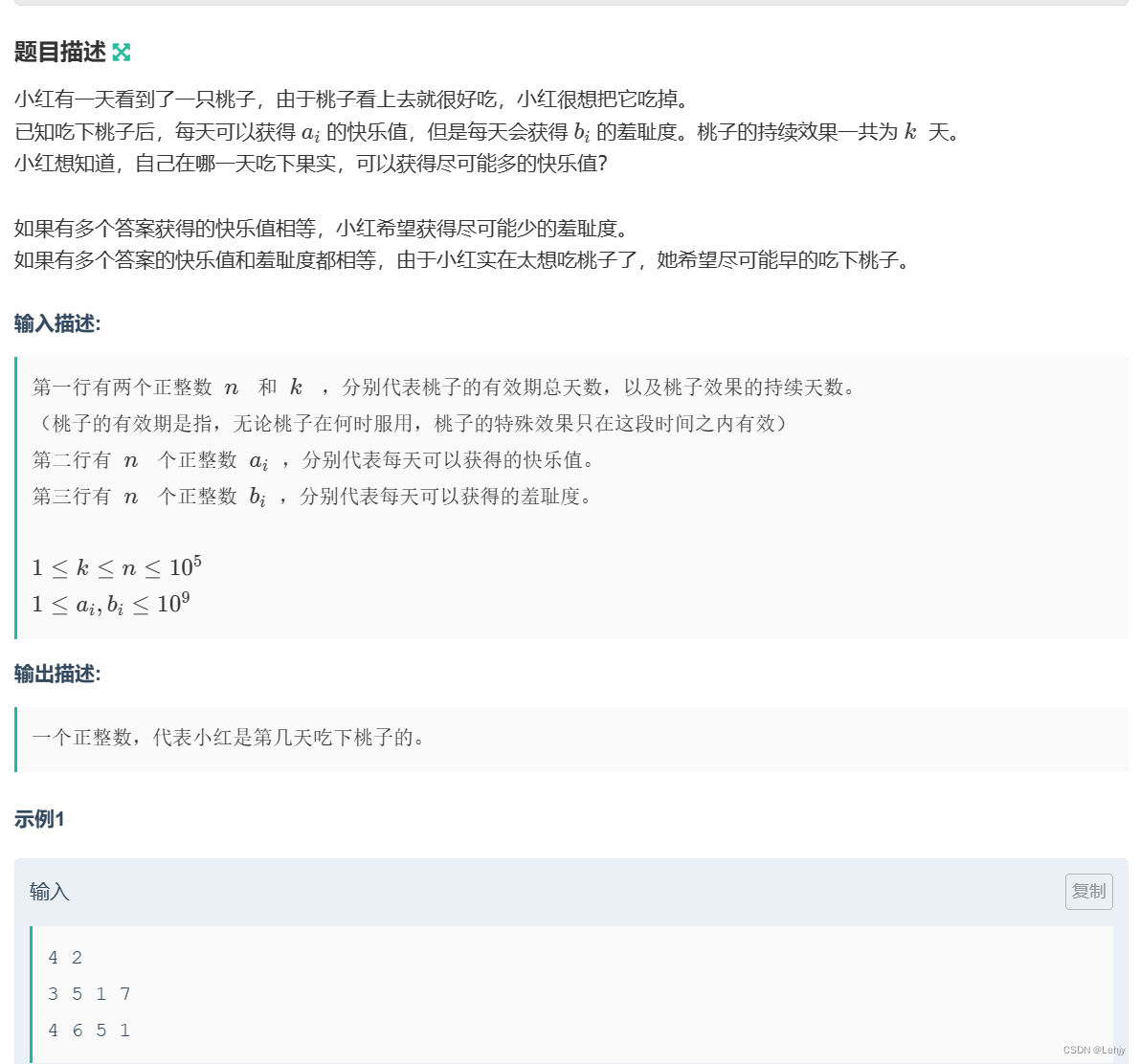
【强训笔记】day17
NO.1 思路:用一个字符串实现,stoi函数可以转化为数字并且去除前导0。 代码实现: #include <iostream> #include<string> using namespace std;string s;int main() {cin>>s;for(int i0;i<s.size();i){if(s[i]%20) s[…...
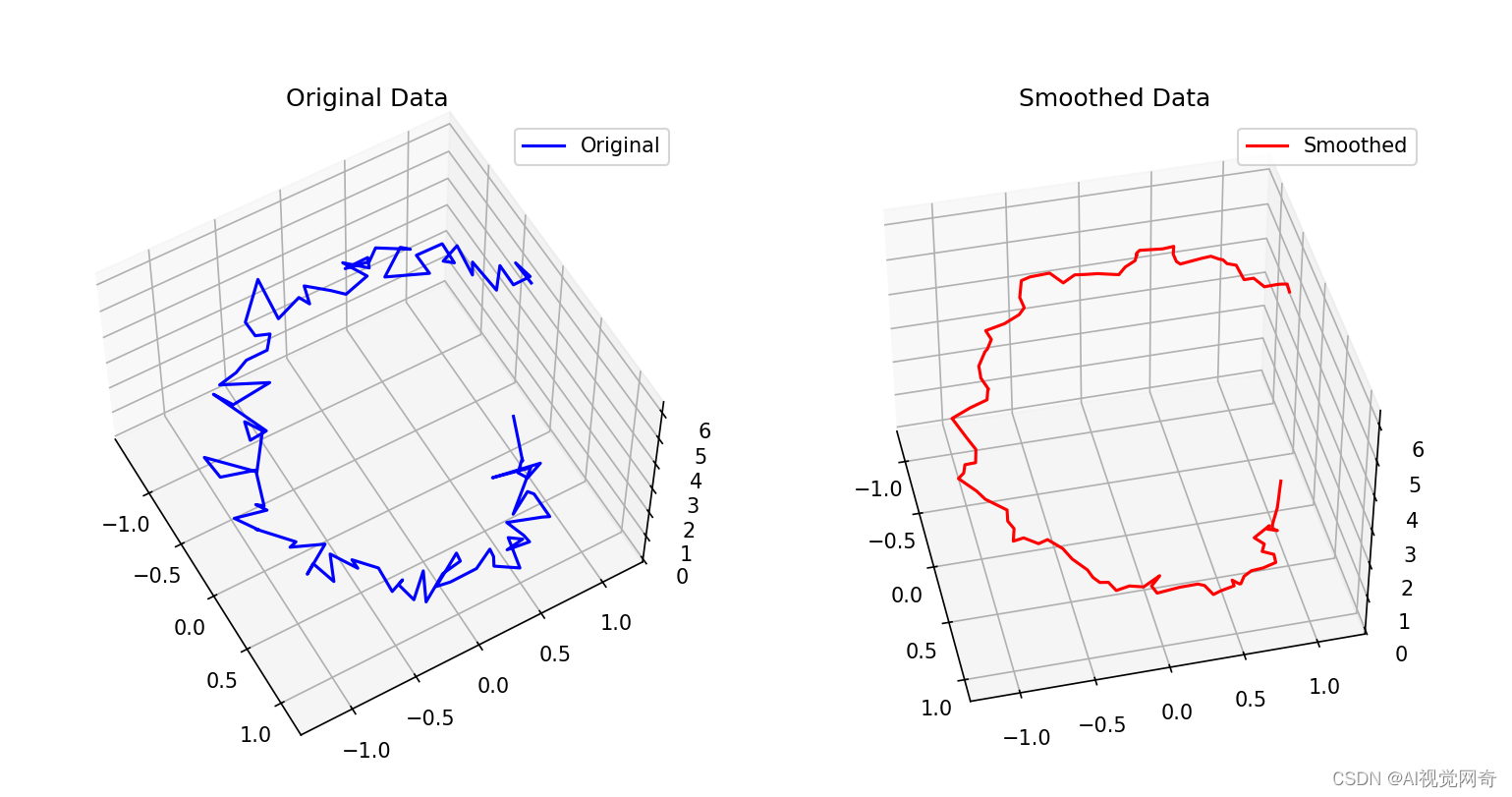
平滑 3d 坐标
3d平滑 import torch import torch.nn.functional as F import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3Dclass SmoothOperator:def smooth(self, vertices):# 使用一维平均池化进行平滑vertices_smooth F.avg_pool1d(vertices.p…...

Go解析的数据类型可能含有不同数据结构的处理方式
最近做一个需求,各种业务消息都会往我的消息队列中写各种类型的数据,服务端需要接受各种不同的参数然后转换为本地数据结构,Go语言不确定上游传过来的数值是什么类型,然后又下面四种解决方案。 1. 类型断言和类型切换 func (Mis…...

Java网络编程基础
Java网络编程基础主要涉及进程间通信、网络通信协议、IP地址和端口以及Java提供的网络应用编程接口等核心概念。 进程间通信是Java网络编程的基础。进程是运行中的程序,而进程间通信则是指不同进程之间进行数据交换和共享信息的过程。在Java中,进程间的…...

鸿蒙DevEco Studio 4.1 Release-模拟器启动方式错误
软件版本:DevEco Studio 4.1 Release 报错提示: 没有权限查看处理指导 Size on Disk 显示1.0MB 尝试方案(统统无效): 1、“windows虚拟机监控程序平台”、"虚拟机平台"已开启 启用CPU虚拟化 2、C…...
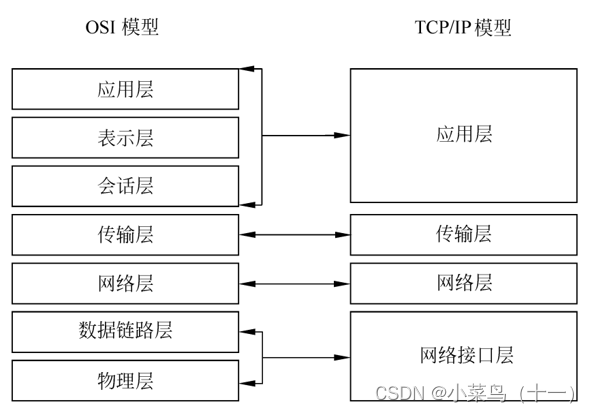
Linux与windows网络管理
文章目录 一、TCP/IP1.1、TCP/IP概念TCP/IP是什么TCP/IP的作用TCP/IP的特点TCP/IP的工作原理 1.2、TCP/IP网络发展史1.3、OSI网络模型1.4、TCP/IP网络模型1.5、linux中配置网络网络配置文件位置DNS配置文件主机名配置文件常用网络查看命令 1.6、windows中配置网络CMD中网络常用…...

一站式、低成本 | 等保一体机安全解决方案
方案建设背景 等级保护是我国关于信息安全的基本政策,相关政策制度要求单位开展等级保护工作。单位信息系统存在的安全隐患和不足,进行安全整改之后,提高信息系统的信息安全防护能力,降低系统被攻击的风险,维护单位良…...

Grafana(CVE-2021-43798)、Apache Druid 代码执行漏洞
文章目录 一、Grafana 8.x 插件模块目录穿越漏洞(CVE-2021-43798)二、Apache Druid 代码执行漏洞(CVE-2021-25646) 一、Grafana 8.x 插件模块目录穿越漏洞(CVE-2021-43798) Grafana是一个系统监测工具。 利…...
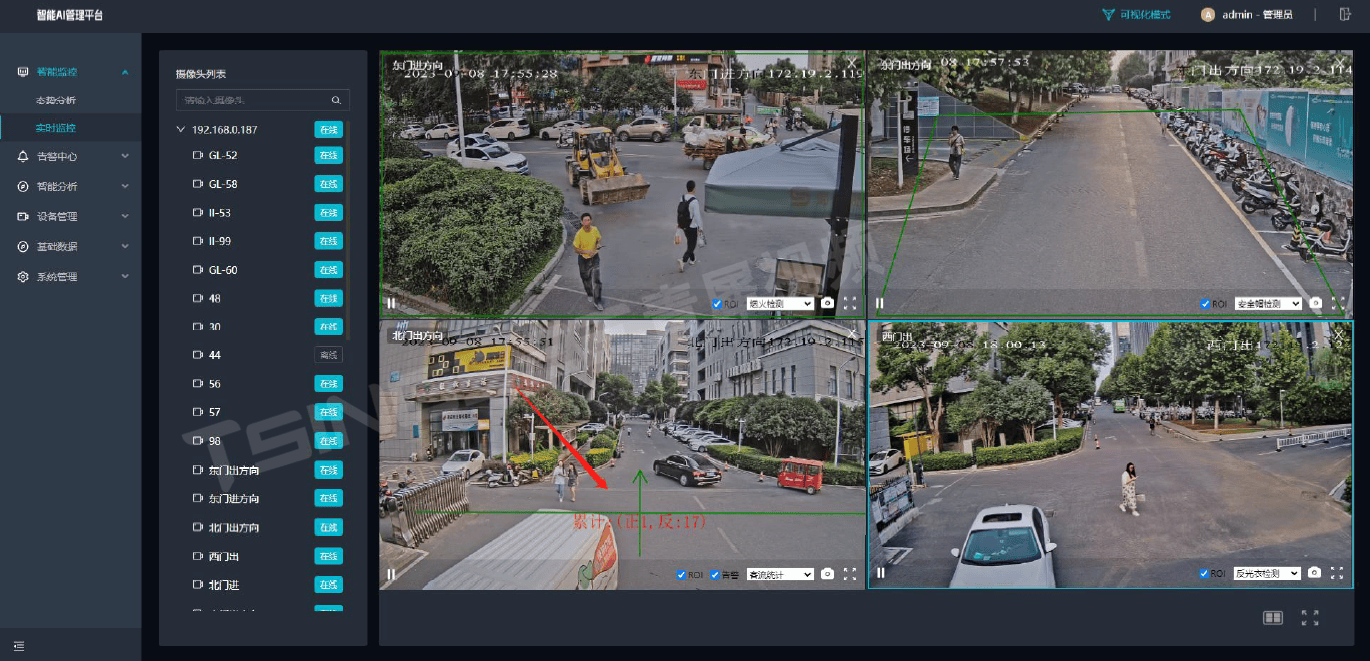
AI赋能EasyCVR视频汇聚/视频监控平台加快医院安防体系数字化转型升级
近来,云南镇雄一医院发生持刀伤人事件持续发酵,目前已造成2人死亡21人受伤。此类事件在医院层出不穷,有的是因为医患纠纷、有的是因为打架斗殴。而且在每日大量流动的人口中,一些不法分子也将罪恶的手伸到了医院,实行扒…...
)
Cocos Creator 3.x 实现触摸拖动物体(record)
参考:如何实现拖动物体 - Creator 3.x - Cocos中文社区 //注册触摸事件 node.on(Node.EventType.TOUCH_MOVE, this.onTouchMove, this); //事件回调函数 onTouchMove(event) {const location event.getUILocation();event.target.setWorldPosition(location.x, lo…...

漏桶算法:稳定处理大量突发流量的秘密武器!
漏桶算法的介绍 我们经常会遇到这样一种情况:数据包的发送速率不稳定,而网络的带宽有限。如果在短时间内有大量的数据包涌入,那么网络就会出现拥塞,数据包的丢失率就会增大。为了解决这个问题,人们提出了一种叫做“漏…...

淘宝数据分析——Python爬虫模式♥
大数据时代, 数据收集不仅是科学研究的基石, 更是企业决策的关键。 然而,如何高效地收集数据 成了摆在我们面前的一项重要任务。 本文将为你揭示, 一系列实时数据采集方法, 助你在信息洪流中, 找到…...
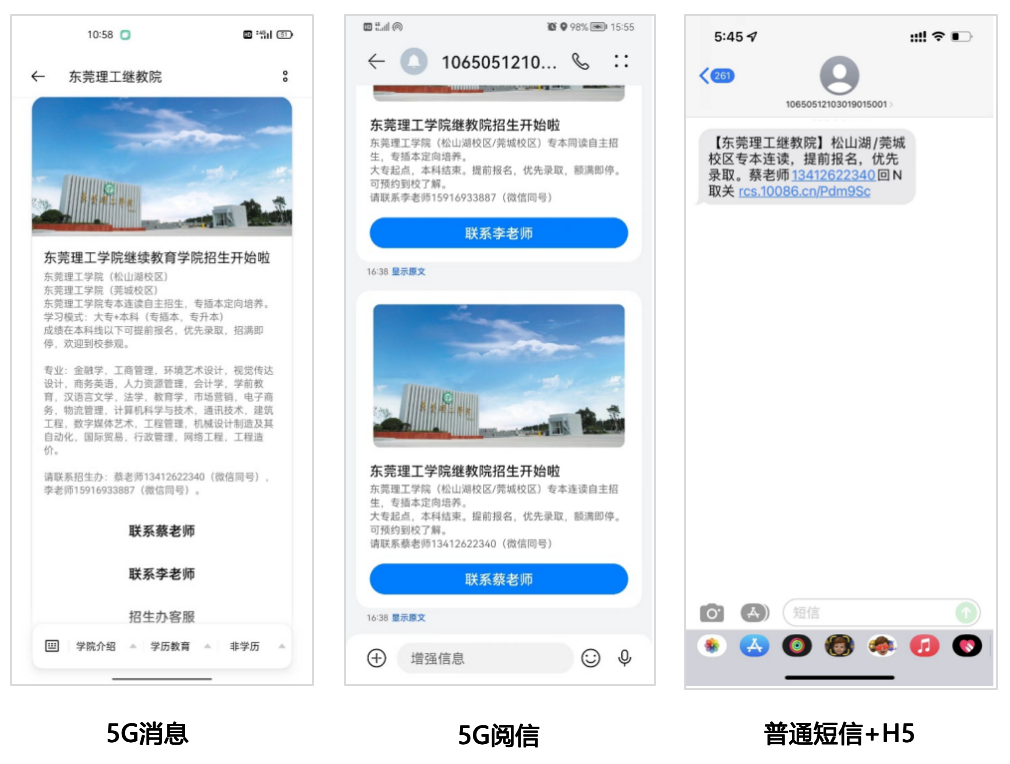
5G消息和5G阅信的释义与区别 | 赛邮科普
5G消息和5G阅信的释义与区别 | 赛邮科普 在 5G 技术全面普及的当下,历史悠久的短信服务也迎来了前所未有的变革。5G 阅信和 5G 消息就是应运而生的两种短信形态,为企业和消费者带来更加丰富的功能和更加优质的体验。 这两个产品名字和形态都比较接近&am…...

数据结构第一次实验
删除进程未完成 代码: #include "stdio.h" #include <stdlib.h> #include <conio.h> #define getpch(type) (type*)malloc(sizeof(type)) #define NULL 0// PCB struct pcb{// char name[10];// char state;// int super;int ntime;int …...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...
