算法学习笔记(LCA)
L C A LCA LCA:树上两个点的最近公共祖先。(两个节点所有公共祖先中,深度最大的公共祖先)
L C A LCA LCA的性质:
- 在所有公共祖先中, L C A ( x , y ) LCA(x,y) LCA(x,y)到 x x x和 y y y的距离都最短。
- x x x, y y y之间最短的路径经过 L C A ( x , y ) LCA(x,y) LCA(x,y)。
- x x x, y y y本身也可以是它们自己的公共祖先。若 y y y是 x x x的祖先,则有 L C A ( x , y ) = y LCA(x,y) = y LCA(x,y)=y。
- L C A ( x , y , z ) = L C A ( x , L C A ( y , z ) ) LCA(x,y,z) = LCA(x, LCA(y,z)) LCA(x,y,z)=LCA(x,LCA(y,z))
- L C A ( x 1 , x 2 , . . . , x n ) = L C A ( d f s 序最大点, d f s 序最小点 ) LCA(x_1, x_2,...,x_n) = LCA(dfs序最大点,dfs序最小点) LCA(x1,x2,...,xn)=LCA(dfs序最大点,dfs序最小点)
本文主要介绍求 L C A LCA LCA的两种方法:倍增法和 T a r j a n Tarjan Tarjan。
先引入例题:
【模板】LCA
题目描述
给定一个 n n n个点以结点 1 1 1为根的树,有 q q q次询问,每次询问给出两个点 u , v u,v u,v,求 L C A ( u , v ) LCA(u,v) LCA(u,v)。
L C A ( u , v ) LCA(u,v) LCA(u,v)表示 u , v u,v u,v的最近公共祖先。
输入描述
第一行一个整数 n n n表示结点个数。 ( 1 ≤ n ≤ 2 × 1 0 5 ) (1 \leq n \leq 2 \times 10^5) (1≤n≤2×105)
第二行 n − 1 n−1 n−1个整数,表示 2 ∼ n 2∼n 2∼n结点的父亲。
第三行一个整数 q q q,表示询问次数。 ( 1 ≤ q ≤ 2 × 1 0 5 ) (1 \leq q \leq 2 \times 10^5) (1≤q≤2×105)
接下来 q q q行,每行两个整数 u , v u,v u,v。 ( 1 ≤ u , v ≤ n ) (1≤u,v≤n) (1≤u,v≤n)
输出描述
对于每次询问,一行一个整数表示结果。
输入样例1
5
1 1 2 3
3
1 2
2 4
1 5
输出样例1
1
2
1
倍增法:
大体就是让两个点不断向上走,直到走到最近的相同的点。如何快速地走?这里就需要用倍增法来实现。倍增法的原理利用了二进制的性质:任意一个数字都可以由一个或几个 2 2 2的幂相加得到,所以可以以 1 , 2 , 4 , 8... 1,2,4,8... 1,2,4,8...这种 2 2 2的幂作为一步的长度向上走。
因为我们不知道应该走多大,所以应该先尝试走大数,能走即走,再尝试走小步。
为了快速地进行跳跃,我们需要预处理出一个帮助我们进行跳跃的数组 f a [ N ] [ 20 ] fa[N][20] fa[N][20]( f a [ x ] [ i ] fa[x][i] fa[x][i]表示从 x x x出发向上走 2 i 2^{i} 2i步到达的位置)。计算 f a fa fa数组时用到了 d p dp dp的思路,这里有个递推公式: f a [ x ] [ i ] = f a [ f a [ x ] [ i − 1 ] ] [ i − 1 ] fa[x][i] = fa[fa[x][i - 1]][i - 1] fa[x][i]=fa[fa[x][i−1]][i−1],意思是从点 x x x出发,先跳 2 i − 1 2 ^ {i - 1} 2i−1步,再跳 2 i − 1 2 ^ {i - 1} 2i−1步。由小推到大。
得到这个数组之后,就可以快速地计算 L C A LCA LCA了。具体步骤如下:
先将点 x x x和点 y y y处理至同一深度。让深度较大的数以祖先链上深度与深度较小的那个点相等的点为目标进行跳跃。特殊的,如果该点就是深度较浅的那个点,则使用上述 L C A LCA LCA的性质中的第三条。
之后,点 x x x和点 y y y再同时向上跳跃。直至分别跳到 L C A ( x , y ) LCA(x,y) LCA(x,y)的两个儿子上。即 x ≠ y x \not = y x=y并且 f a [ x ] [ 0 ] = f a [ y ] [ 0 ] fa[x][0] = fa[y][0] fa[x][0]=fa[y][0]。
最后得到的 f a [ x ] [ 0 ] fa[x][0] fa[x][0]就是 L C A ( x , y ) LCA(x,y) LCA(x,y)。
时间复杂度为: O ( n l o g 2 n + q l o g 2 n ) O(nlog_2n + qlog_2n) O(nlog2n+qlog2n)
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 9, T = 20;vector<int> g[N];
int fa[N][30], dep[N];void dfs(int x)
{dep[x] = dep[fa[x][0]] + 1; //预处理各个节点深度//预处理fa数组for(int i = 1; i <= T; ++i) fa[x][i] = fa[fa[x][i - 1]][i - 1];for(const auto &i : g[x]){dfs(i);}
}int lca(int u, int v)
{if(dep[u] < dep[v]) swap(u, v); //不妨设点u深度大于等于点v//跳跃,先走大步再走小步//将u点跳至于点v相同高度for(int i = T; i >= 0; --i){if(dep[fa[u][i]] >= dep[v]) u = fa[u][i];}if(u == v) return u;//一起往上跳for(int i = T; i >= 0; --i){if(fa[u][i] != fa[v][i]) u = fa[u][i], v = fa[v][i];}return fa[u][0];
}int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int n; cin >> n;for(int i = 2; i <= n; ++i){cin >> fa[i][0];g[fa[i][0]].push_back(i);}dfs(1);int q; cin >> q;while(q--){int u, v; cin >> u >> v;cout << lca(u, v) << '\n';}return 0;
}
Tarjan
大概流程:
还是采用 d f s dfs dfs,访问到一个点的时候,先标记被访问,然后向下处理它的儿子节点,看儿子节点是否为所求 L C A LCA LCA有关的点,处理完儿子节点之后回溯上来时再处理自己,看自己是否为所求 L C A LCA LCA有关的点。再向上合并,合并采用并查集进行合并且使用路径压缩。
因为有多组询问,所以需要将询问离线。
对于一对点中的一个点处理的时候,若另一个点已经被访问过了,那么那个点在的并查集中的根节点就是它们的 L C A LCA LCA,这和 d f s dfs dfs的性质有关。都访问到的时候,它们一定在同一棵子树上,并且这颗子树的根显然就是它们的 L C A LCA LCA。
时间复杂度为: O ( n + q ) O(n + q) O(n+q)
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 9;int pre[N], dep[N], ans[N], fa[N];
vector<int> g[N];
vector<pair<int, int>> Q[N];
bitset<N> vis;//并查集基础操作
int find(int x)
{return pre[x] = (pre[x] == x ? x : find(pre[x]));
}void merge(int x, int y) //将深度大的向深度小的合并,向上合并
{int fx = find(x), fy = find(y);if(dep[fx] < dep[fy]) swap(fx, fy);pre[fx] = fy;
}void dfs(int x)
{//顺手计算深度,合并时使用dep[x] = dep[fa[x]] + 1;vis[x] = true;for(const auto &y : g[x]) dfs(y); //先处理所有儿子for(const auto &[y, id] : Q[x]) //在处理自己{if(!vis[y]) continue; //如果对方未被访问就跳过ans[id] = find(y);}merge(x, fa[x]);
}void solve()
{int n; cin >> n;for(int i = 1; i <= n; ++i) pre[i] = i;for(int i = 2; i <= n; ++i){cin >> fa[i];g[fa[i]].push_back(i);}int q; cin >> q;//将询问离线for(int i = 1; i <= q; ++i){int x, y; cin >> x >> y;Q[x].push_back({y, i});Q[y].push_back({x, i});}dfs(1);for(int i = 1; i <= q; ++i) cout << ans[i] << '\n';
}int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int _ = 1;while(_--) solve();return 0;
}
L C A LCA LCA可以求树上两点之间的最短距离,也可以做树上差分,这里就不过多赘述。
相关文章:
)
算法学习笔记(LCA)
L C A LCA LCA:树上两个点的最近公共祖先。(两个节点所有公共祖先中,深度最大的公共祖先) L C A LCA LCA的性质: 在所有公共祖先中, L C A ( x , y ) LCA(x,y) LCA(x,y)到 x x x和 y y y的距离都最短。 x …...

记一次苹果appstore提审拒审问题1.2
有关苹果appstore审核1.2问题的处理方案 2023.8.6苹果回复 Bug Fix Submissions The issues weve identified below are eligible to be resolved on your next update. If this submission includes bug fixes and youd like to have it approved at this time, reply to thi…...
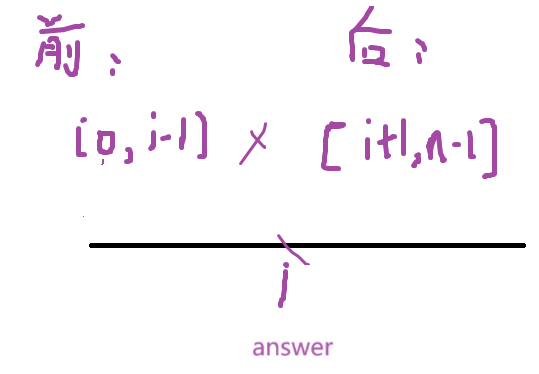
在做题中学习(59):除自身以为数组的乘积
238. 除自身以外数组的乘积 - 力扣(LeetCode) 解法:前缀积和后缀积 思路:answer中的每一个元素都是除自己以外所有元素的和。那就处理一个前缀积数组和后缀积数组。 而前缀积(f[i])是:[0,i-1]所有元素的乘积 后缀…...

centos 把nginx更新到最新版本
yum install epel-release # 添加 EPEL 软件仓库,这是 Nginx 官方软件仓库的依赖项 yum install yum-utils # yum-utils 包含了 yum-config-manager 工具,它可以让您轻松地启用、禁用或配置 yum 软件仓库 vi /etc/yum.repos.d/nginx.repo # 增加以下内容…...
01.认识HTML及常用标签
目录 URL(统一资源定位系统) HTML(超文本标记语言) 1)html标签 2)head标签 3)title标签 4)body标签 标签的分类 DTD文档声明 基础标签 1)H系列标签 2)…...

从零开始:C++ String类的模拟实现
文章目录 引言1.类的基本结构2.构造函数和析构函数3.基本成员函数总结 引言 在C编程中,字符串操作是非常常见且重要的任务。标准库中的std::string类提供了丰富且强大的功能,使得字符串处理变得相对简单。然而,对于学习C的开发者来说&#x…...
银河麒麟服务器操作系统V10-SP2部署gitlab服务
安装依赖 yum -y install python3-policycoreutils openssh-server openssh-clients postfix cronie curl下载gitlab-ce-15.4.2-ce.0.el8.x86_64.rpm安装包。 wget --content-disposition https://packages.gitlab.com/gitlab/gitlab-ce/packages/el/8/gitlab-ce-15.4.2-ce.0…...
【计算机毕业设计】基于SSM+Vue的线上旅行信息管理系统【源码+lw+部署文档+讲解】
目录 1 绪论 1.1 研究背景 1.2 设计原则 1.3 论文组织结构 2 系统关键技术 2.1JSP技术 2.2 JAVA技术 2.3 B/S结构 2.4 MYSQL数据库 3 系统分析 3.1 可行性分析 3.1.1 技术可行性 3.1.2 操作可行性 3.1.3 经济可行性 3.1.4 法律可行性 3.2系统功能分析 3.2.1管理员功能分析 3.2.…...

链表CPP简单示例
链表创建 链表打印全部内容 获取链表长度 链表根据指定位置添加元素 链表根据指定位置删除元素 #include <iostream> using namespace std;// 1、创建结构体// typedef 经常在结构中使用 typedef 别名 typedef struct node {int date;struct node* next; // 必须要自己…...

智能EDM邮件群发工具哪个好?
企业之间的竞争日益激烈,如何高效、精准地触达目标客户,成为每个市场战略家必须面对的挑战。在此背景下,云衔科技凭借其前沿的AI技术和深厚的行业洞察,匠心推出了全方位一站式智能EDM邮件营销服务平台,重新定义了邮件营…...

低代码与AI技术发展:开启数字化新时代
随着数字化转型的深入推进,低代码和AI技术逐渐成为各行各业关注的焦点。这两种技术的发展不仅改变了传统开发模式,还为企业创新和产业升级提供了新契机。本文将探讨这两种技术在实际应用中的相互促进作用,以及它们为我国经济社会发展带来的机…...

风电功率预测 | 基于遗传算法优化BP神经网络实现风电功率预测(附matlab完整源码)
风电功率预测 风电功率预测 | 基于遗传算法优化BP神经网络实现风电功率预测(附matlab完整源码)完整代码风电功率预测 | 基于遗传算法优化BP神经网络实现风电功率预测(附matlab完整源码) 基于遗传算法优化BP神经网络是一种常见的方法,用于改进BP神经网络在风电功率预测中的性…...

uni-segmented-control插件使用
dcloud插件市场 前端/uniapp 1.HBuildX打开目标项目 2.进入dcloud插件市场下载目标插件 3.看到如下提示(已经可以在目标项目中使用插件啦) 4.项目正式使用...

被动防护不如主动出击
自网络的诞生以来,攻击威胁事件不断涌现,网络攻防对抗已然成为信息时代背景下的一场无硝烟的战争。然而,传统的网络防御技术,如防火墙和入侵检测技术,往往局限于一种被动的敌暗我明的防御模式,面对攻击者无…...
ollama离线部署llama3(window系统)
首先介绍下ollama是什么?Ollama是一个开源的大型语言模型服务工具,旨在为用户提供本地化的运行环境,满足个性化的需求。具体来说,Ollama是一个功能强大的开源框架,可以简化在Docker容器中部署和管理大型语言模型&a…...

基于Django实现的(bert)深度学习文本相似度检测系统设计
基于Django实现的(bert)深度学习文本相似度检测系统设计 开发语言:Python 数据库:MySQL所用到的知识:Django框架工具:pycharm、Navicat、Maven 系统功能实现 登录页面 注册页面:用户账号,密码…...
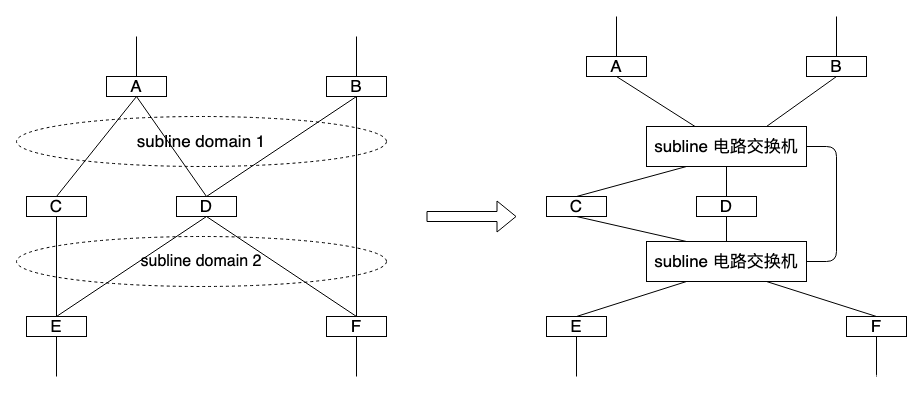
数据中心网络随想-电路交换
数据中心网络扩容并不容易,涉及设备上架,切换等又硬又大的动作,期间对所有应用都会产生影响,所以理论上 “加钱加硬件” 这种看起来很简单的事实际上真不如 “写一个随时部署升级的端到端拥塞控制算法” 更容易实施。 傍晚绕小区…...
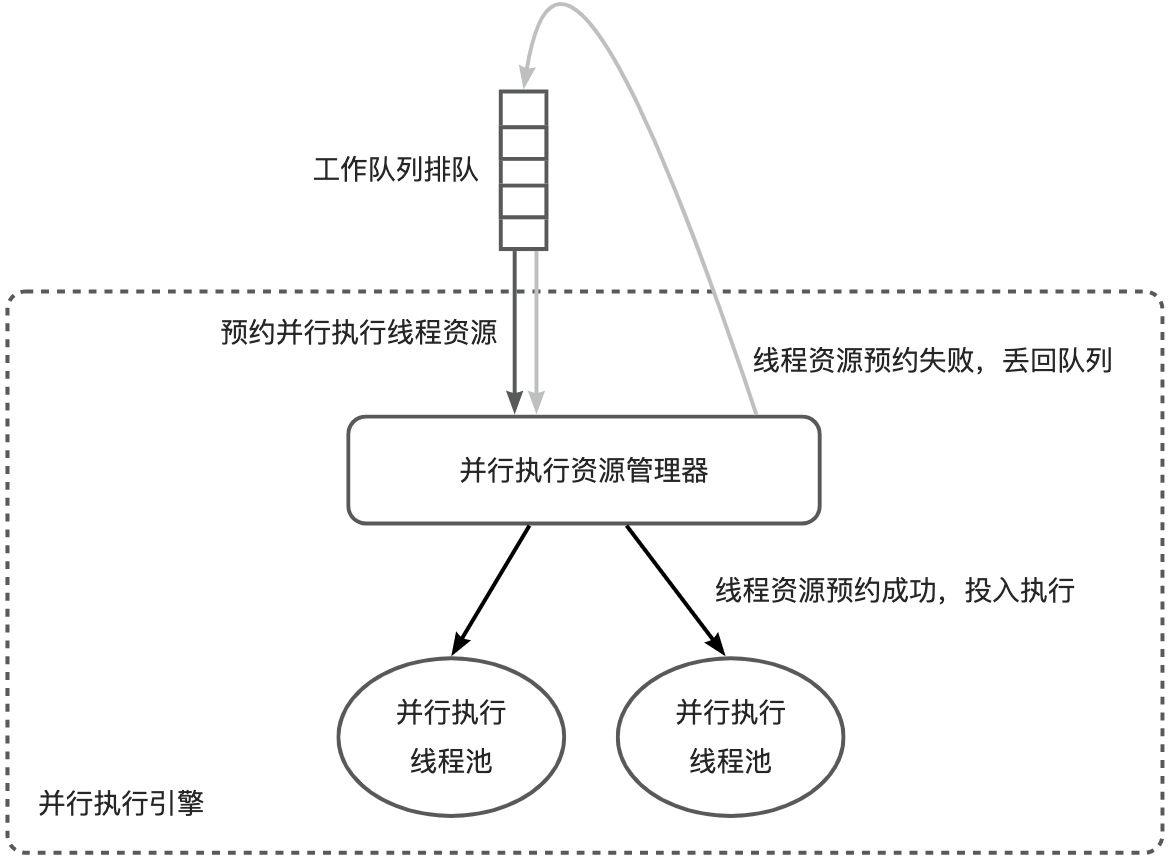
并行执行线程资源管理方式——《OceanBase 并行执行》系列 3
在某些特定场景下,由于需要等待线程资源,并行查询会遇到排队等待的情况。本篇博客将介绍如何管理并行执行线程资源,以解决这种问题。 《OceanBase并行执行》系列的内容分为七篇博客,本篇是其中的第三篇。 一并行执行概念二如何手…...

数据库系统概论(个人笔记)(第二部分)
数据库系统概论(个人笔记) 文章目录 数据库系统概论(个人笔记)2、关系模型简介2.1 关系数据库的结构2.2 数据库模式2.3 键2.4 模式图2.5 关系查询语言2.6 关系代数 2、关系模型简介 2.1 关系数据库的结构 Structure of Relational…...
WebView基础知识以及Androidx-WebKit的使用
文章目录 摘要WebView基础一、启动调整模式二、WebChromeClient三、WebViewClient四、WebSettings五、WebView和Native交互 Androidx-WebKit一、启动安全浏览服务二、设置代理三、安全的 WebView 和 Native 通信支持四、文件传递五、深色主题的支持六、JavaScript and WebAssem…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...
