Linux第四节--常见的指令介绍集合(持续更新中)
点赞关注不迷路!本节涉及初识Linux第四节,主要为常见的几条指令介绍。
如果文章对你有帮助的话
欢迎 评论💬 点赞👍🏻 收藏 ✨ 加关注👀期待与你共同进步!
1. more指令
语法:more [选项][文件]
功能:more命令,功能类似 cat
常用选项: -n 对输出的所有行编号 q 退出more
举例:
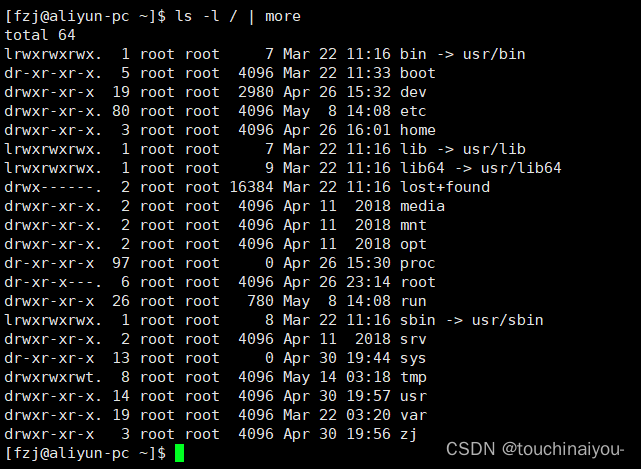
2. less指令
less 工具也是对文件或其它输出进行分页显示的工具,应该说是linux正统查看文件内容的工具,功能极其强大。less 的用法比起 more 更加的有弹性。在 more 的时候,我们并没有办法向前面翻, 只能往后面看但若使用了 less 时,就可以使用 [pageup] [pagedown] 等按键的功能来往前往后翻看文件,更容易用来查看一个文件的内容!
除此之外,在 less 里头可以拥有更多的搜索功能,不止可以向下搜,也可以向上搜
语法: less [参数] 文件
功能:
less与more类似,但使用less可以随意浏览文件,而more仅能向前移动,却不能向后移动,而且less在查看之前不会加载整个文件。
选项:
-i 忽略搜索时的大小写
-N 显示每行的行号
/字符串:向下搜索“字符串”的功能
?字符串:向上搜索“字符串”的功能
n:重复前一个搜索(与 / 或 ? 有关)
N:反向重复前一个搜索(与 / 或 ? 有关)
q:quit
3. head指令
head 与 tail 就像它的名字一样的浅显易懂,它是用来显示开头或结尾某个数量的文字区块,head 用来显示档案的开头至标准输出中,而 tail 想当然尔就是看档案的结尾。
语法: head [参数]... [文件]...
功能:
head 用来显示档案的开头至标准输出中,默认head命令打印其相应文件的开头10行。
选项:-n<行数> 显示的行数
4. tail指令
tail 命令从指定点开始将文件写到标准输出.使用tail命令的-f选项可以方便的查阅正在改变的日志文件,tail -f filename会把filename里最尾部的内容显示在屏幕上,并且不但刷新,使你看到最新的文件内容.
语法: tail[必要参数][选择参数][文件]
功能: 用于显示指定文件末尾内容,不指定文件时,作为输入信息进行处理。
常用查看日志文件。
选项:-f 循环读取
-n<行数> 显示行数
举例:(简单讲解重定向和管道)
有一个文件共有100行内容,请取出第50行内容<br>
seq 1 100 > test # 生成1到100的序列装入test
方法1 head -n50 test > tmp #将前50行装入临时文件tmp
tail -n1 tmp #得到中建行
方法2 head -n50 test | tail -n1
点赞关注不迷路!本节涉及初识Linux第四节,主要为常见的几条指令介绍。
如果文章对你有帮助的话
欢迎 评论💬 点赞👍🏻 收藏 ✨ 加关注👀期待与你共同进步!
相关文章:

Linux第四节--常见的指令介绍集合(持续更新中)
点赞关注不迷路!本节涉及初识Linux第四节,主要为常见的几条指令介绍。 如果文章对你有帮助的话 欢迎 评论💬 点赞👍🏻 收藏 ✨ 加关注👀 期待与你共同进步! 1. more指令 语法:more [选项][文件]…...
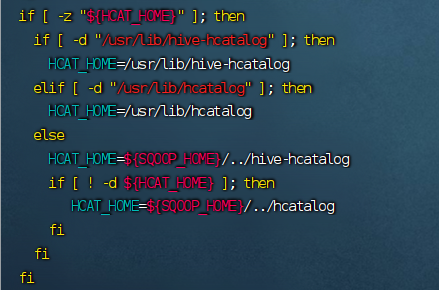
Apache Sqoop:高效数据传输工具搭建与使用教程
目录 引言一、环境准备二、安装sqoop下载sqoop包解压文件 三、配置Sqoop下载mysql驱动拷贝hive的归档文件配置环境变量修改sqoop-env.sh配置文件替换版本的commons-lang的jar包 验证Sqoop安装查看Sqoop版本测试Sqoop连接MySQL数据库是否成功查看数据库查看数据表去除警告信息 四…...
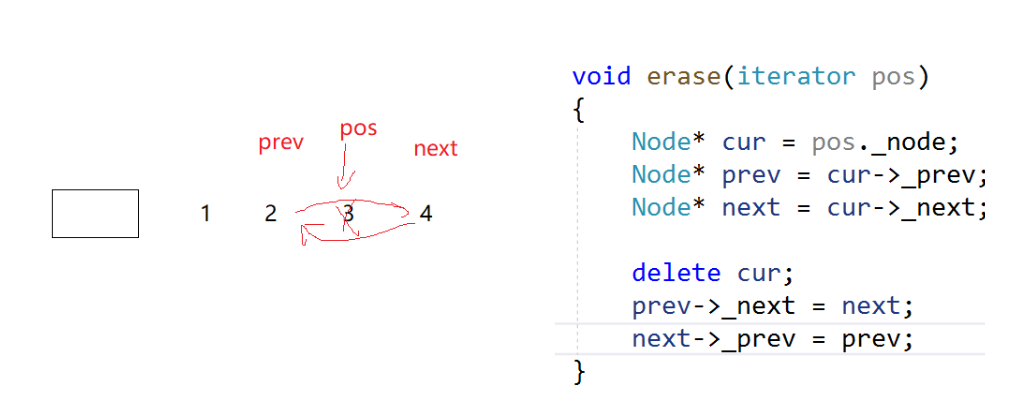
【C++初阶】第十一站:list的介绍及使用
目录 list的介绍及使用 1.list的含义 2.list的介绍 3.list的使用 1.list的构造 2.list iterator的使用 3.list capacity 4.list element access 5 list modifiers 尾插尾删 和 头插头删 insert 和 erase resize swap clear 6.list sort and reverse 7.list copy vector copy li…...

【devops】Linux 日常磁盘清理 ubuntu 清理大文件 docker 镜像清理
日常磁盘清理 1、查找大文件 find / -type f -size 1G2、清理docker无用镜像(drone产生的残余镜像文件) docker system prune -a一、清理服务器磁盘 1、查找大文件 在Ubuntu系统中,你可以使用find命令来查找大文件。find命令是一个强大的…...

2024年资阳市企业技术中心申报条件、流程要求及支持政策须知
第一章 总则 第一条 为深入贯彻中央、省、市大力实施创新驱动发展战略的部署要求,进一步强化企业技术创新主体地位,引导和支持企业增强技术创新能力,健全技术创新市场导向机制,规范我市企业技术中心(下称“市企业技术…...

社交媒体数据恢复:如流
如流,原名百度Hi,是百度公司开发的一款即时通讯软体。百度Hi具备文字消息、视讯、通话、文件传输等功能。 查找备份:如果您之前有备份如流中的数据,您可以尝试从备份中恢复。如流支持备份至云端,如百度网盘等。 联系客…...

【微信小程序开发(从零到一)【婚礼邀请函】制作】——任务分析和效果实现的前期准备(1)
👨💻个人主页:开发者-曼亿点 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 曼亿点 原创 👨💻 收录于专栏:…...

独孤思维:模仿别人赚钱太难,很痛苦
01 独孤早年混群的时候,想着成为群红,引流。 结果不得其法,别人要什么项目,我就把满是钩子的副业资料发群里。 被群主踢了出去。 我当时还不理解。 后来自己做了社群以后,才明白,这种行为,…...

图片转base64【Vue + 纯Html】
1.template <el-form-item label"图片"><div class"image-upload-container"><input type"file" id"imageUpload" class"image-upload" change"convertToBase64" /><label for"imageU…...

【从零开始学习Redis | 第十一篇】快速介绍Redis持久化策略
前言: Redis 作为一种快速、高效的内存数据库,被广泛应用于缓存、消息队列、会话存储等场景。然而,由于其特性是基于内存的,一旦服务器进程退出,内存中的数据就会丢失。为了解决这一问题,Redis 提供了持久…...

在Ubuntu中如何解压zip压缩包??
2024年5月15日,周三上午 使用 unzip 命令 unzip 文件名.zip这会将压缩包中的内容解压到当前目录。如果想解压到特定目录,可以使用 -d 选项,例如: unzip 文件名.zip -d 目标目录使用 7-zip 还可以安装 7-zip 工具来解压 ZIP 文件。…...

LeetCode 126题:单词接龙 II
❤️❤️❤️ 欢迎来到我的博客。希望您能在这里找到既有价值又有趣的内容,和我一起探索、学习和成长。欢迎评论区畅所欲言、享受知识的乐趣! 推荐:数据分析螺丝钉的首页 格物致知 终身学习 期待您的关注 导航: LeetCode解锁100…...
)
5.14(Vue2)
1.单页应用程序是指所有功能都在一个html页面上 单页面应用程序,之所以开发效率高,性能好,应用体验好,最大的原因就是:页面按需更新。 2.Vue中的路由 路径和组件的映射关系 Vue中的路由插件:VueRouter&…...

使用openssl生成自签名证书
使用openssl生成自签名证书 1. 交互式生成2. 一步生成参考 1. 交互式生成 自签名 SSL 证书的生成涉及一个简单的 3 步过程: 步骤 1:创建服务器私钥 openssl genrsa -out cert.key 2048步骤 2:创建证书签名请求 (CSR) openssl req -new -k…...
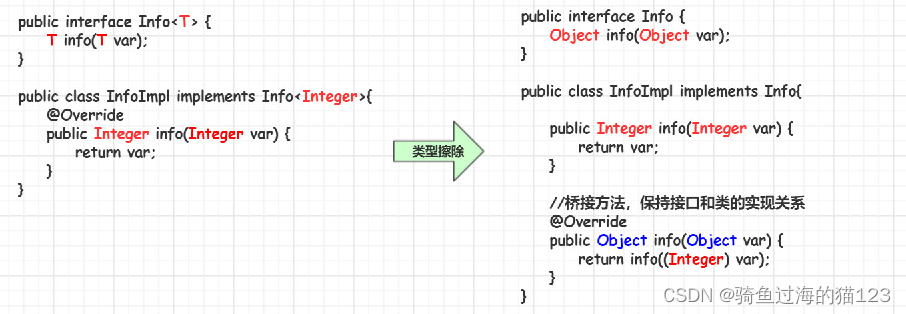
【java】泛型
文章目录 1. 什么是泛型?1.1 背景1.2 泛型的概念1.3 泛型的好处 2. 泛型类、接口...2.1 泛型类2.2 从泛型类派生子类2.2.1 子类也是泛型类,子类和父类的泛型类型要一致2.2.2 子类不是泛型类,父类要明确泛型的数据类型 2.3 泛型接口2.4 泛型方…...

计算思维的理解
2006年,卡内基梅隆大学周以真教授首次系统性地定义了计算思维。这一年,她在美国计算机权威期刊《Communications of the ACM》上发表了题为《Computational Thinking》的论文,由此开启了计算思维大众化的全新历程。 周以真(Jeanne…...
Python中tkinter编程入门4
在Python中tkinter编程入门3-CSDN博客中创建了Button控件,点击该控件就会产生一个点击事件,在创建Button控件时指定该点击事件的处理程序后,按键控件就会对用户的点击事件产生响应。 1 定义事件处理器 定义事件处理器就是一个自定义的函数。…...
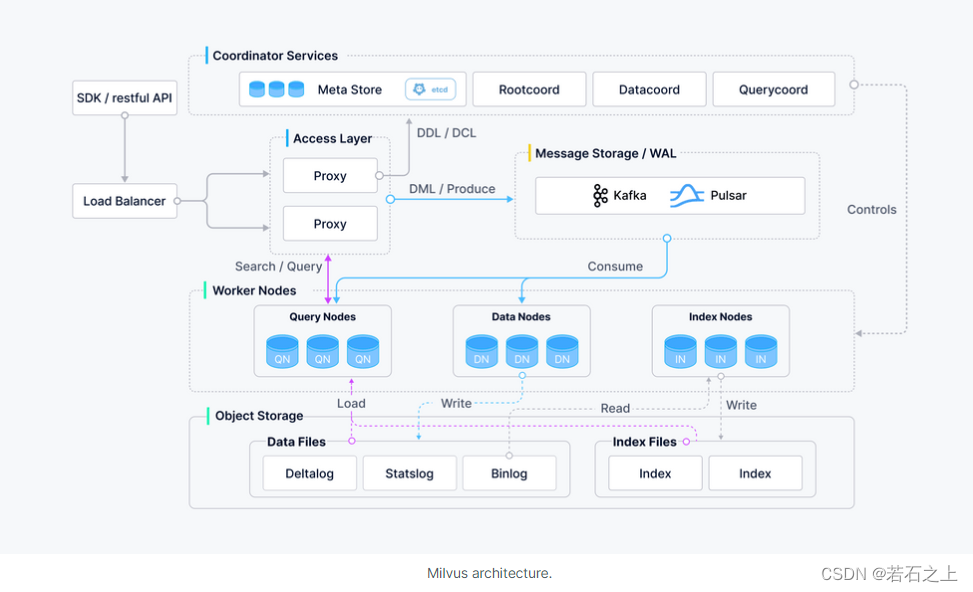
Milvus的系统架构
简介 Milvus的构建在许多知名的向量搜索库比如Faiss, HNSW, DiskANN, SCANN等之上的,它针对稠密向量数据集的相似搜索而设计,能支持百万、十亿甚至万亿级别的向量搜索。 Milvus支持数据分片,流式数据插入,动态schema,…...

MFC中关于CMutex类的学习
MFC中关于CMutex类的学习 最近在项目中要实现两个线程之间的同步,MFC中提供了4个类,分别是CMutex(互斥量)、CCriticalSection(临界区)、CEvent(事件对象)、CSemaphore(信号量)。有关这4个类的说明,大家可以参考微软官方文档: CM…...

删除表空间
Oracle从入门到总裁:https://blog.csdn.net/weixin_67859959/article/details/135209645 当某个表空间中的数据不再需要时,或者新创建的表空间不符合要求时,可以考虑删除这个表空间。若要删除表空间,则需要用户具有 DROP TABLESP…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...
