嵌入式开发四大平台介绍
MCU(Micro Control Unit)四大平台介绍)
- 单片机
- 优点:
- 缺点:
- 总结:
- DSP digital signal processing
- ARM
- 优点:
- 缺点:
- 总结
- FPGA
- 什么事FPGA(集成元件库)
- FPGA开发方法——
- FPGA三大方向
- FPGA缺点:
- FPGA优点——On chip to rule them all
- 总结:
- 总结
- 典型应用场景:
- 未来发展方向:
- 基本学习路线:
单片机
优点:
1.结构简单(体积小,价格低,功耗低)
2.开发时间短
3.有诸多现成接口:I2C,SPI,AD,PWM
缺点:
1.速度低(几十兆-百兆)(一般是冯诺依曼结构)
2.接口不够丰富(没有USB OTG、网口、MIPI、SATA等)
总结:
1.适合控制
2.不适合 算法、数据传输、高速数据处理
DSP digital signal processing
数字滤波器
高吞吐量(哈弗结构)
高处理速度(主频高、硬件卷积运算(累加器、硬件乘法器、桶形移位寄存器))
总结:
1.适合处理单路串行信号、运行DSP算法
2.不适合控制
ARM
优点:
1.能装OS——线程调度
2.接口丰富——以太网、USB、MIPI、SATA,只要OS支持
3.配置灵活——丰富点CPU、简单点单片机、也能做视频解决方案等
缺点:
1.软件开发门槛更高
2.器件更加复杂(体积大、价格高、功耗高)
总结
1.适合 数据处理、数据传输、CPU
2.不适合 ?? 感觉没有
FPGA
什么事FPGA(集成元件库)
1.导线——wire
2.寄存器——reg
3.乘法器
4.时钟管理器——PLL、DCM、MMCM
5.存储器——RAM、双口RAM、FIFO
6.存储控制器——DDR2、3、4
6.高速串行器——光纤、PCIE、SATA
7.CPU
单片机(软)——Microblaze(TM)
x86(硬)——IBM PowerPC
ARM(硬)——7系列以后,Zync
8.AD转换器
FPGA开发方法——
硬件描述语言HDL——开发套件画电路——
综合 把HDL转成原理图
实现 把原理图变成电路图
FPGA三大方向
1.逻辑开发——时序发生
2.DSP开发——雷达
3.嵌入式开发——ARM+处理电路
FPGA缺点:
1.价格高
2.接口不丰富
3.开发门槛高,周期长
4.外围器件多,PCB设计复杂
5.体积大,功耗高
FPGA优点——On chip to rule them all
总结:
1.适合 并行高速信号处理、芯片设计前期验证、不值得流片的高端设计
2.不适合 低成本
总结
典型应用场景:
单片机——白色家电等
DSP——视频直播
ARM——各种应用
FPGA——芯片验证、高端应用
未来发展方向:
单片机——精简的ARM(比如STM32)
DSP——加了DSP硬件的ARM——ARM9(哈弗结构)、TI的DSP集成C-M4核
ARM——加了各种专用电路的ARM(SOC)
FPGA——带了可编程电路的ARM
基本学习路线:
1.简单的单片机STM32
2.STM32+RTOS(学完这里的时候软件硬件都要会了)
3.ARM处理器+Linux
相关文章:

嵌入式开发四大平台介绍
MCU(Micro Control Unit)四大平台介绍) 单片机优点:缺点:总结: DSP digital signal processingARM优点:缺点:总结 FPGA什么事FPGA(集成元件库)FPGA开发方法—…...
《Python编程从入门到实践》day28
# 昨日知识点回顾 安装Matplotlib 绘制简单的折线图 # 今日知识点学习 15.2.1 修改标签文字和线条粗细 # module backend_interagg has no attribute FigureCanvas. Did you mean: FigureCanvasAgg? # 解决办法:matplotlib切换图形界面显示终端TkAgg。 #…...
STC8增强型单片机开发【定时器Timer⭐】
目录 一、引言 二、定时器基础知识 三、STC8定时器配置 四、代码示例 五、总结 一、引言 在单片机开发中,定时器(Timer)是一个极其重要的组件,它允许开发者基于时间触发各种事件或任务。STC8增强型单片机作为一款功能丰富的…...

C语言实训项目源码-02餐厅饭卡管理系统-C语言实训C语言大作业小项目
C语言餐厅饭卡管理系统 一、主要功能 主要功能模块 页面名称 实现功能 负责人 进入页面 进入程序 主函数 系统主要功能 修改密码函数 修改密码 充值,显示函数 饭卡充值与信息显示 购买饭菜…...
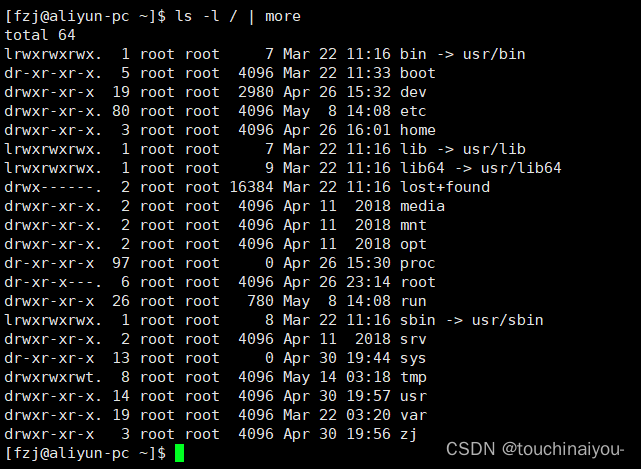
Linux第四节--常见的指令介绍集合(持续更新中)
点赞关注不迷路!本节涉及初识Linux第四节,主要为常见的几条指令介绍。 如果文章对你有帮助的话 欢迎 评论💬 点赞👍🏻 收藏 ✨ 加关注👀 期待与你共同进步! 1. more指令 语法:more [选项][文件]…...
Apache Sqoop:高效数据传输工具搭建与使用教程
目录 引言一、环境准备二、安装sqoop下载sqoop包解压文件 三、配置Sqoop下载mysql驱动拷贝hive的归档文件配置环境变量修改sqoop-env.sh配置文件替换版本的commons-lang的jar包 验证Sqoop安装查看Sqoop版本测试Sqoop连接MySQL数据库是否成功查看数据库查看数据表去除警告信息 四…...
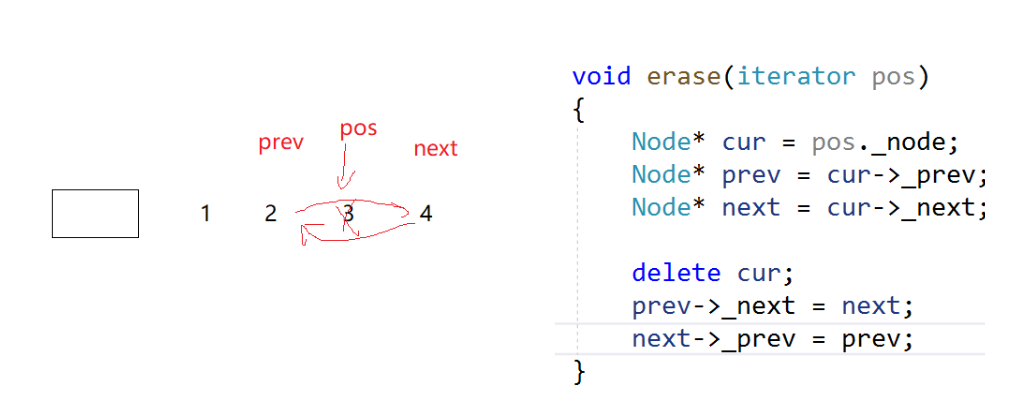
【C++初阶】第十一站:list的介绍及使用
目录 list的介绍及使用 1.list的含义 2.list的介绍 3.list的使用 1.list的构造 2.list iterator的使用 3.list capacity 4.list element access 5 list modifiers 尾插尾删 和 头插头删 insert 和 erase resize swap clear 6.list sort and reverse 7.list copy vector copy li…...

【devops】Linux 日常磁盘清理 ubuntu 清理大文件 docker 镜像清理
日常磁盘清理 1、查找大文件 find / -type f -size 1G2、清理docker无用镜像(drone产生的残余镜像文件) docker system prune -a一、清理服务器磁盘 1、查找大文件 在Ubuntu系统中,你可以使用find命令来查找大文件。find命令是一个强大的…...

2024年资阳市企业技术中心申报条件、流程要求及支持政策须知
第一章 总则 第一条 为深入贯彻中央、省、市大力实施创新驱动发展战略的部署要求,进一步强化企业技术创新主体地位,引导和支持企业增强技术创新能力,健全技术创新市场导向机制,规范我市企业技术中心(下称“市企业技术…...

社交媒体数据恢复:如流
如流,原名百度Hi,是百度公司开发的一款即时通讯软体。百度Hi具备文字消息、视讯、通话、文件传输等功能。 查找备份:如果您之前有备份如流中的数据,您可以尝试从备份中恢复。如流支持备份至云端,如百度网盘等。 联系客…...

【微信小程序开发(从零到一)【婚礼邀请函】制作】——任务分析和效果实现的前期准备(1)
👨💻个人主页:开发者-曼亿点 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 曼亿点 原创 👨💻 收录于专栏:…...

独孤思维:模仿别人赚钱太难,很痛苦
01 独孤早年混群的时候,想着成为群红,引流。 结果不得其法,别人要什么项目,我就把满是钩子的副业资料发群里。 被群主踢了出去。 我当时还不理解。 后来自己做了社群以后,才明白,这种行为,…...

图片转base64【Vue + 纯Html】
1.template <el-form-item label"图片"><div class"image-upload-container"><input type"file" id"imageUpload" class"image-upload" change"convertToBase64" /><label for"imageU…...

【从零开始学习Redis | 第十一篇】快速介绍Redis持久化策略
前言: Redis 作为一种快速、高效的内存数据库,被广泛应用于缓存、消息队列、会话存储等场景。然而,由于其特性是基于内存的,一旦服务器进程退出,内存中的数据就会丢失。为了解决这一问题,Redis 提供了持久…...

在Ubuntu中如何解压zip压缩包??
2024年5月15日,周三上午 使用 unzip 命令 unzip 文件名.zip这会将压缩包中的内容解压到当前目录。如果想解压到特定目录,可以使用 -d 选项,例如: unzip 文件名.zip -d 目标目录使用 7-zip 还可以安装 7-zip 工具来解压 ZIP 文件。…...

LeetCode 126题:单词接龙 II
❤️❤️❤️ 欢迎来到我的博客。希望您能在这里找到既有价值又有趣的内容,和我一起探索、学习和成长。欢迎评论区畅所欲言、享受知识的乐趣! 推荐:数据分析螺丝钉的首页 格物致知 终身学习 期待您的关注 导航: LeetCode解锁100…...
)
5.14(Vue2)
1.单页应用程序是指所有功能都在一个html页面上 单页面应用程序,之所以开发效率高,性能好,应用体验好,最大的原因就是:页面按需更新。 2.Vue中的路由 路径和组件的映射关系 Vue中的路由插件:VueRouter&…...

使用openssl生成自签名证书
使用openssl生成自签名证书 1. 交互式生成2. 一步生成参考 1. 交互式生成 自签名 SSL 证书的生成涉及一个简单的 3 步过程: 步骤 1:创建服务器私钥 openssl genrsa -out cert.key 2048步骤 2:创建证书签名请求 (CSR) openssl req -new -k…...
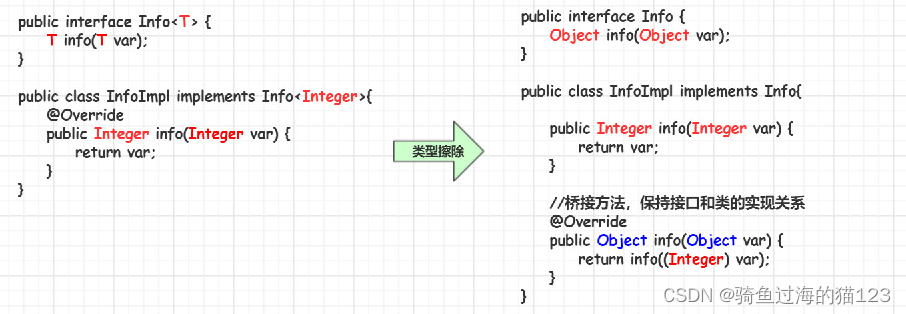
【java】泛型
文章目录 1. 什么是泛型?1.1 背景1.2 泛型的概念1.3 泛型的好处 2. 泛型类、接口...2.1 泛型类2.2 从泛型类派生子类2.2.1 子类也是泛型类,子类和父类的泛型类型要一致2.2.2 子类不是泛型类,父类要明确泛型的数据类型 2.3 泛型接口2.4 泛型方…...

计算思维的理解
2006年,卡内基梅隆大学周以真教授首次系统性地定义了计算思维。这一年,她在美国计算机权威期刊《Communications of the ACM》上发表了题为《Computational Thinking》的论文,由此开启了计算思维大众化的全新历程。 周以真(Jeanne…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...
