【回溯】1240. 铺瓷砖
本文涉及知识点
回溯
LeetCode1240. 铺瓷砖
你是一位施工队的工长,根据设计师的要求准备为一套设计风格独特的房子进行室内装修。
房子的客厅大小为 n x m,为保持极简的风格,需要使用尽可能少的 正方形 瓷砖来铺盖地面。
假设正方形瓷砖的规格不限,边长都是整数。
请你帮设计师计算一下,最少需要用到多少块方形瓷砖?
示例 1:

输入:n = 2, m = 3
输出:3
解释:3 块地砖就可以铺满卧室。
2 块 1x1 地砖
1 块 2x2 地砖
示例 2:

输入:n = 5, m = 8
输出:5
示例 3:
输入:n = 11, m = 13
输出:6

提示:
1 <= n <= 13
1 <= m <= 13
回溯
aHas[r][c] 记录第r行,第c列是否已经铺设瓷砖。
先行后列处理第一个没有铺设的单格,从大到小尝试铺设瓷砖。
回溯最后一个层次:所有单格都已经铺满瓷砖。回溯结束:使用的磁盘是否小于结果。
一层回溯:
GetNext获取下一个没有铺瓷砖的单元格格。
如果所有单格都铺了瓷砖,则本次回溯失败。
计算最大能铺maxLen的瓷砖。注意:右下可能已有瓷砖。2*2的瓷砖无法放下。

len = maxLen :1
将len所在单格铺上瓷砖
回溯下一层次
将len所在单格瓷砖取消
小技巧
如果cnt已经大于等于res,则直接返回。
r,c 不必从0,0开始,从r,c+len开始。如果c+len >= m,则r++,c=0。
回溯代码
核心代码
template<class ELE,class ELE2>
void MinSelf(ELE* seft, const ELE2& other)
{*seft = min(*seft,(ELE) other);
}template<class ELE>
void MaxSelf(ELE* seft, const ELE& other)
{*seft = max(*seft, other);
}class Solution {
public:int tilingRectangle(int n, int m) {bool vHas[13][13] = { false };int iRet = n * m;auto GetNext = [&](int& r, int& c) {if (c >= m) {r++;c = 0;}if (r >= n) { return true; };if (!vHas[r][c]) { return true; }c++;return false;};std::function<void(int, int,int)> BackTrack = [&](int r, int c,int cnt) {if (cnt >= iRet) { return; }while (!GetNext(r, c));if (r >= n) {iRet = min(iRet, cnt);return;}int maxLen = min(n - r, m - c);for (int i = r; i < r + maxLen; i++) {for (int j = c; j < c + maxLen; j++) {if (vHas[i][j]) {MinSelf(&maxLen, i - r);MinSelf(&maxLen, j - c);}}}for (int len = maxLen; len > 0; len--) {for (int i = r; i < r + len; i++) {for (int j = c; j < c + len; j++) {vHas[i][j] = true;}}BackTrack(r, c + len, cnt + 1);for (int i = r; i < r + len; i++) {for (int j = c; j < c + len; j++) {vHas[i][j] = false;}}} }; BackTrack(0, 0, 0);return iRet;}
};
测试用例
template<class T>
void Assert(const vector<T>& v1, const vector<T>& v2)
{if (v1.size() != v2.size()){assert(false);return;}for (int i = 0; i < v1.size(); i++){assert(v1[i] == v2[i]);}
}template<class T>
void Assert(const T& t1, const T& t2)
{assert(t1 == t2);
}int main()
{{Solution slu;auto res = slu.tilingRectangle(1, 1);Assert(1, res);}{Solution slu;auto res = slu.tilingRectangle(1, 2);Assert(2, res);}{Solution slu; auto res = slu.tilingRectangle(2, 3);Assert(3, res);}{Solution slu;auto res = slu.tilingRectangle(5, 8);Assert(5, res);}{Solution slu;auto res = slu.tilingRectangle(11, 13);Assert(6, res);}
}

扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 《喜缺全书算法册》以原理、正确性证明、总结为主。 |
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【回溯】1240. 铺瓷砖
本文涉及知识点 回溯 LeetCode1240. 铺瓷砖 你是一位施工队的工长,根据设计师的要求准备为一套设计风格独特的房子进行室内装修。 房子的客厅大小为 n x m,为保持极简的风格,需要使用尽可能少的 正方形 瓷砖来铺盖地面。 假设正方形瓷砖的…...

【Unity Shader入门精要 第7章】基础纹理(一)
1. 纹理映射 每一张纹理可以看作拥有一个属于自己的2D坐标空间,其横轴用U表示,纵轴用V表示,因此也称为UV坐标空间。 UV空间的坐标范围为[0,0]到[1,1],在Unity中,UV空间也是从左下到右上&#…...

el-checkbox选中后的值为id,组件显示为label中文
直接上代码 方法一 <el-checkbox v-for"item in list" :key"item.id" :label"item.id">{{中文}} </el-checkbox> 方法二 <el-checkbox-group class"flex_check" v-model"rkStatusList" v-for"item…...

03-数据结构(一)
链接:C# 数据结构_哔哩哔哩_bilibili https://www.bilibili.com/video/BV1a541147Nk/?spm_id_from333.337.search-card.all.click&vd_source6eb7d966aa03ff5cb02b63725f651e68 链接:使用 C#.Net 学习掌握数据结构 (更新中)_哔哩哔哩_bilibili 一…...

MySQL问题记录-主机被锁问题
主机被锁问题 描述:"Host ‘113.109.111.217’ is blocked because of many connection errors 原因:同一个ip在短时间内产生太多中断的数据库连接而导致的阻塞; 超过mysql数据库max_connection_errors的最大值; 解决方法…...

用好 explain 妈妈再也不用担心我的 SQL 慢了
大家好,我是聪,一个乐于分享的小小程序员。在不久之前我写了一个慢 SQL 分析工具,可以用来分析 Java Mybatis 项目的 SQL 执行情况,其中刚好涉及到了 explain 的使用。感兴趣的可以了解一下。 Github 地址⭐:https://…...
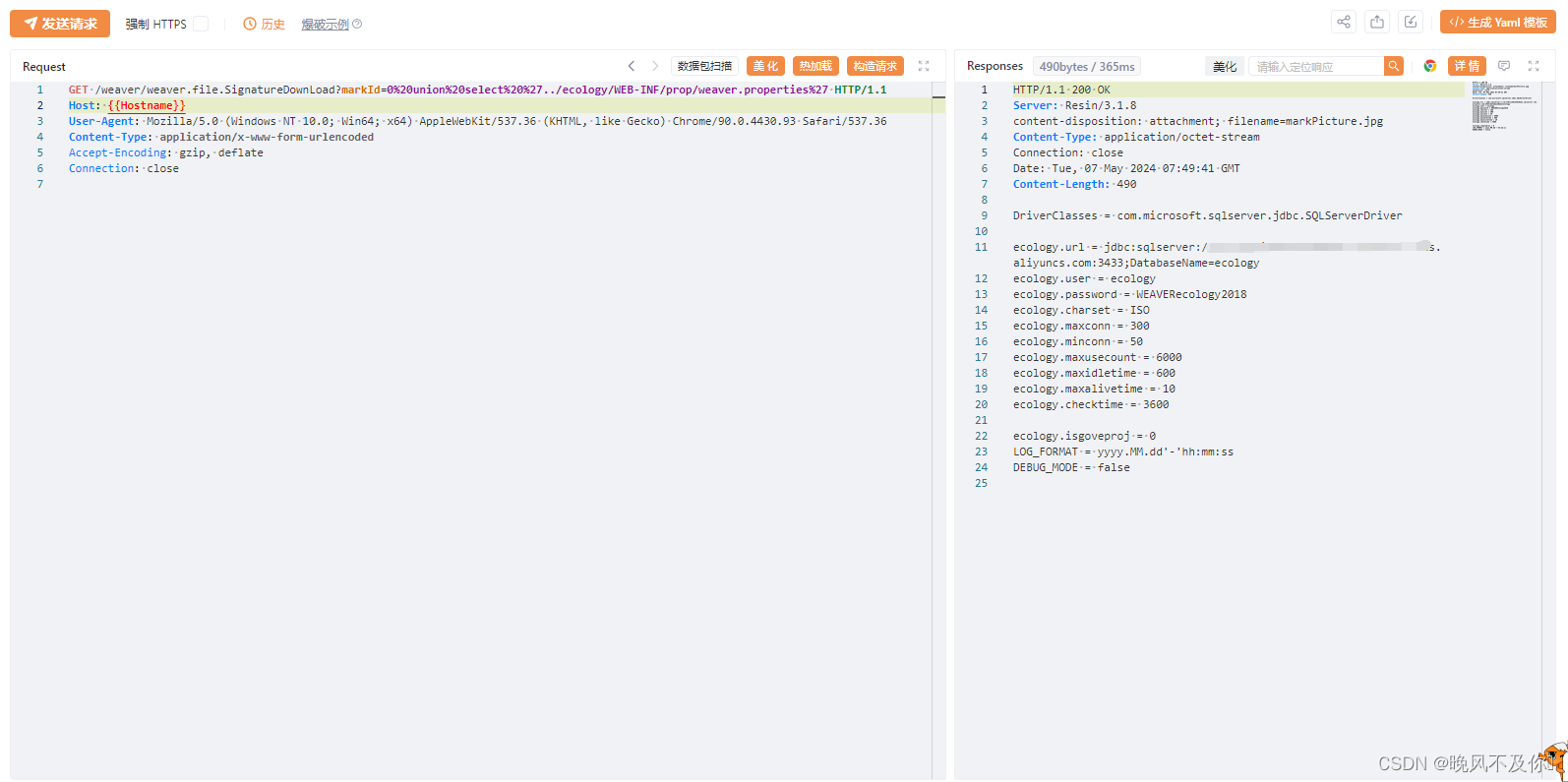
【漏洞复现】泛微OA E-Cology SignatureDownLoad SQL注入漏洞
漏洞描述: 泛微OA E-Cology是一款面向中大型组织的数字化办公产品,它基于全新的设计理念和管理思想,旨在为中大型组织创建一个全新的高效协同办公环境。泛微OA E-Cology SignatureDownLoad存在SQL注入漏洞,允许攻击者非法访问和操…...
前端工程化,前端监控,工作流,部署,性能
开发规范 创建项目的时候,配置下 ESlint,stylelint, prettier, commitlint 等; ESLint 主要功能: ESLint 是一个静态代码检查工具,用于在 JavaScript 代码中识别和报告模式。它的目标是提供一个插件化的 …...

浅析Java贪心算法
浅析Java贪心算法 在计算机科学中,贪心算法(Greedy Algorithm)是一种在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望导致结果是全局最好或最优的算法。贪心算法并不总是能够得到全…...
vue3.0(五) reactive全家桶
文章目录 1 reactive1.1 reactive的应用1.2 reactive的特点1.3 reactive的注意1.4 reactive的局限性 2 toRefs3 isReactive4 shallowReactive5 readonly5.1 readonly 详细信息5.2 readonly函数创建一个只读的响应式对象5.3 如何修改嵌套在只读响应式对象中的对象? 6 isReadonl…...

Selenium 自动化 —— 四种等待(wait)机制
更多关于Selenium的知识请访问CSND论坛“兰亭序咖啡”的专栏:专栏《Selenium 从入门到精通》 目录 目录 需要等待的场景 自己实现等待逻辑 Selenium 提供的三种等待机制 隐式等待(Implicit Waits) 隐式等待的优点 隐式等待的缺点 …...
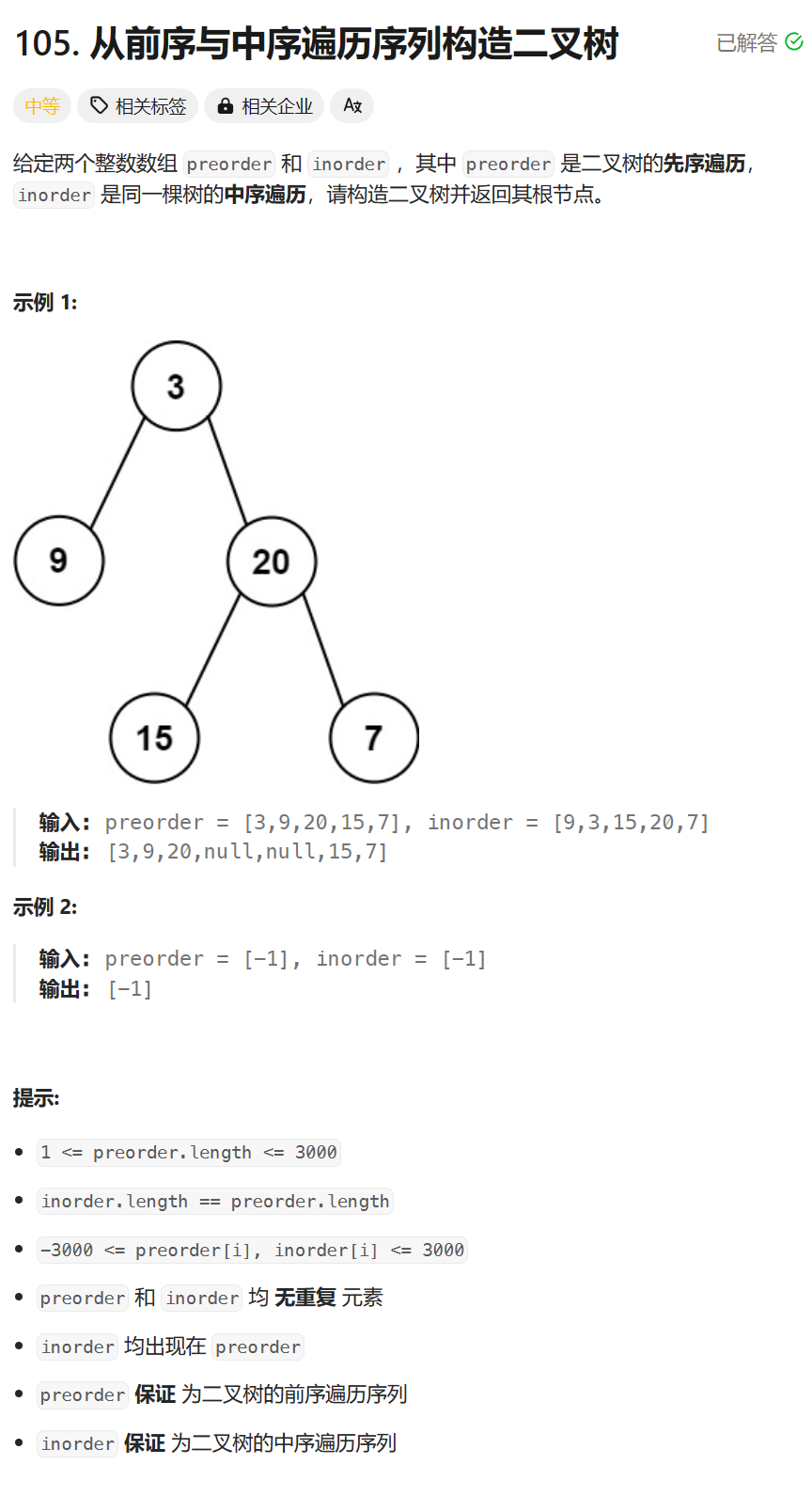
每日两题 / 437. 路径总和 III 105. 从前序与中序遍历序列构造二叉树(LeetCode热题100)
437. 路径总和 III - 力扣(LeetCode) 前序遍历时,维护当前路径(根节点开始)的路径和,同时记录路径上每个节点的路径和 假设当前路径和为cur,那么ans 路径和(cur - target)的出现次数 /*** D…...
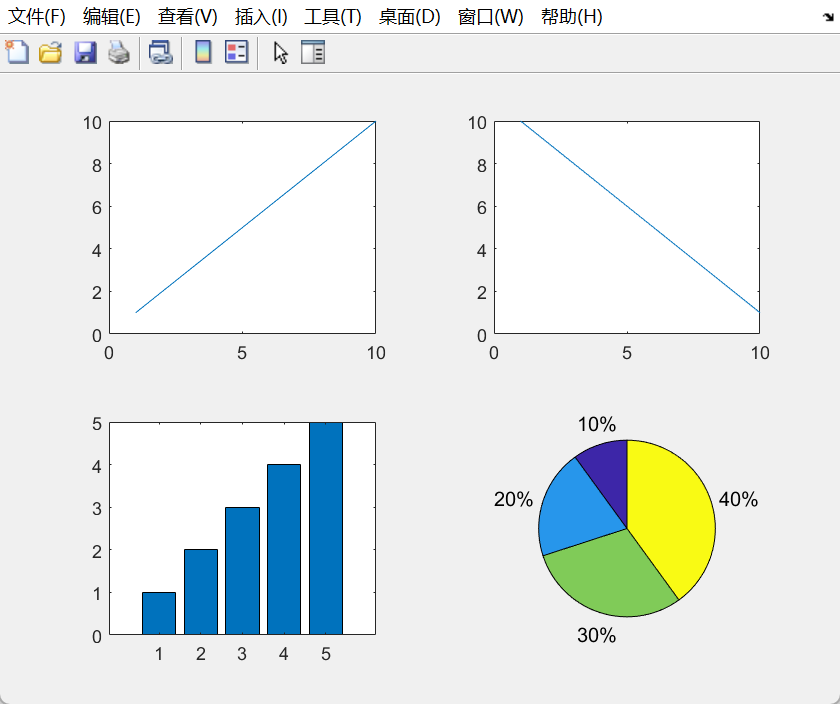
matlab使用2-基础绘图
matlab使用2-基础绘图 文章目录 matlab使用2-基础绘图1. 二维平面绘图2. 三维立体绘图3. 图形窗口的分割 1. 二维平面绘图 % 创建一些二维数据 x 0:0.01:10; % x轴的数据点,从0到10,间隔为0.01 y sin(x); % y轴的数据点,是x的正弦…...

嵌入式开发四大平台介绍
MCU(Micro Control Unit)四大平台介绍) 单片机优点:缺点:总结: DSP digital signal processingARM优点:缺点:总结 FPGA什么事FPGA(集成元件库)FPGA开发方法—…...
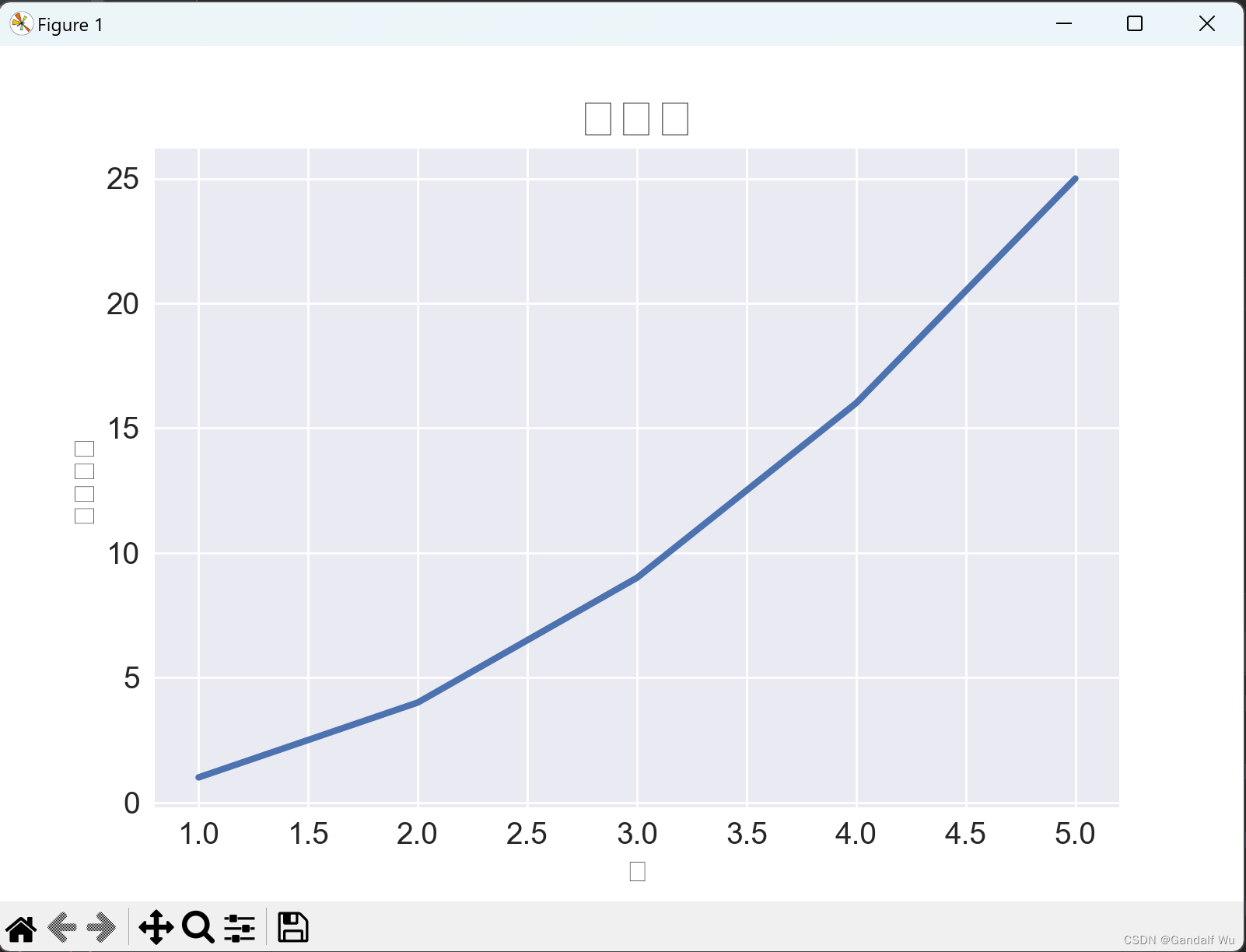
《Python编程从入门到实践》day28
# 昨日知识点回顾 安装Matplotlib 绘制简单的折线图 # 今日知识点学习 15.2.1 修改标签文字和线条粗细 # module backend_interagg has no attribute FigureCanvas. Did you mean: FigureCanvasAgg? # 解决办法:matplotlib切换图形界面显示终端TkAgg。 #…...
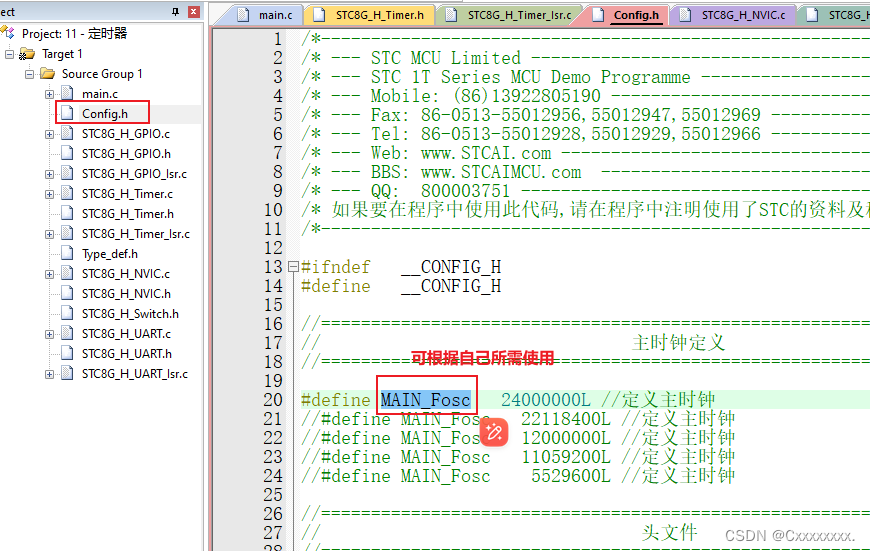
STC8增强型单片机开发【定时器Timer⭐】
目录 一、引言 二、定时器基础知识 三、STC8定时器配置 四、代码示例 五、总结 一、引言 在单片机开发中,定时器(Timer)是一个极其重要的组件,它允许开发者基于时间触发各种事件或任务。STC8增强型单片机作为一款功能丰富的…...

C语言实训项目源码-02餐厅饭卡管理系统-C语言实训C语言大作业小项目
C语言餐厅饭卡管理系统 一、主要功能 主要功能模块 页面名称 实现功能 负责人 进入页面 进入程序 主函数 系统主要功能 修改密码函数 修改密码 充值,显示函数 饭卡充值与信息显示 购买饭菜…...
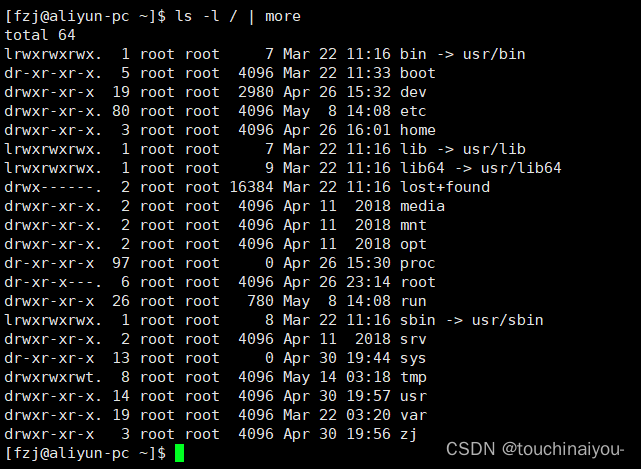
Linux第四节--常见的指令介绍集合(持续更新中)
点赞关注不迷路!本节涉及初识Linux第四节,主要为常见的几条指令介绍。 如果文章对你有帮助的话 欢迎 评论💬 点赞👍🏻 收藏 ✨ 加关注👀 期待与你共同进步! 1. more指令 语法:more [选项][文件]…...
Apache Sqoop:高效数据传输工具搭建与使用教程
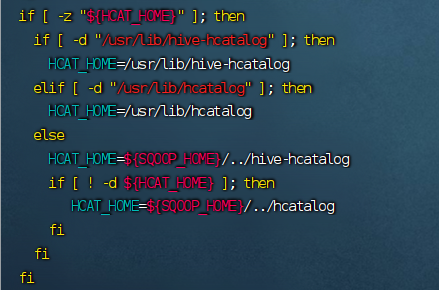
目录 引言一、环境准备二、安装sqoop下载sqoop包解压文件 三、配置Sqoop下载mysql驱动拷贝hive的归档文件配置环境变量修改sqoop-env.sh配置文件替换版本的commons-lang的jar包 验证Sqoop安装查看Sqoop版本测试Sqoop连接MySQL数据库是否成功查看数据库查看数据表去除警告信息 四…...
【C++初阶】第十一站:list的介绍及使用
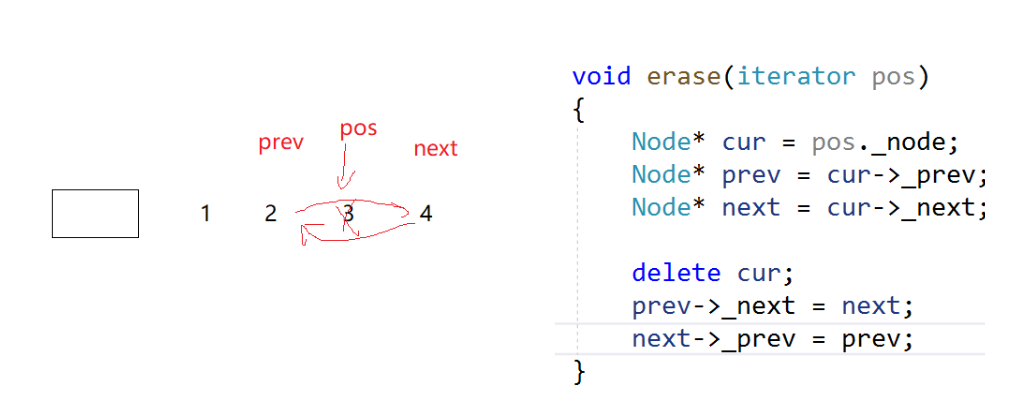
目录 list的介绍及使用 1.list的含义 2.list的介绍 3.list的使用 1.list的构造 2.list iterator的使用 3.list capacity 4.list element access 5 list modifiers 尾插尾删 和 头插头删 insert 和 erase resize swap clear 6.list sort and reverse 7.list copy vector copy li…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...
