Hive建表高阶语句
CTAS -as select方式建表
CREATE TABLE ctas_employee as SELECT * FROM employee;CTE (CTAS with Common Table Expression)
CREATE TABLE cte_employee AS
WITH
r1 AS (SELECT name FROM r2 WHERE name = 'Michael'),
r2 AS (SELECT name FROM employee WHERE gender= 'Male'),
r3 AS (SELECT name FROM employee WHERE gender = 'Female')
SELECT * FROM r1 UNION ALL SELECT * FROM r3;LIKE
CREATE TABLE employee_like LIKE employee;创建临时表--temporary
临时表是应用程序自动管理在复杂查询期间生成的中间数据的方法
表只对当前session有效,session退出后自动删除
表空间位于/tmp/hive-<user_name>(安全考虑)
如果创建的临时表表名已存在,实际用的是临时表
CREATE TEMPORARY TABLE tmp_table_name1 (c1 string);
CREATE TEMPORARY TABLE tmp_table_name2 AS..
CREATE TEMPORARY TABLE tmp_table_name3 LIKE..清空表数据--truncate
TRUNCATE TABLE employee; 创建动态分区
---动态分区需设定属性
set hive.exec.dynamic.partition=true; ---是否开启动态分区
set hive.exec.dynamic.partition.mode=nonstrict;
---建表
create table employee_dt(name string,workplace array<string>,skills_score map<string,int>,depart_title map<string,string>
) partitioned by (gender string,age int )row format delimited fields terminated by ','collection items terminated by '-'map keys terminated by ':'lines terminated by "\n";动态表插入数据
/*将employeept中的数据导入到employee_dt表中*/
insert into table employee_dt partition (age,gender)
select name, workplace, skills_score, depart_title,gender,agefrom employee2;查询分区
show partitions employee_dt;添加分区
alter table employee_dtadd partition (gender = "Male",age = 28);删除分区
alter table employee_dtdrop partition (gender = "Male",age = 28);修改表(alter针对元数据)
改名
alter table employee rename to new_employee;修正表文件格式
alter table employee set fileformat rcfile; 修改列名
alter table employee change name employee_name string; 添加列
alter table employee add columns (work string);替换列
alter table employee replace columns (name string);Hive视图(view)
视图:通过隐藏子查询、连接和函数来简化查询的逻辑结构;只保存定义,不存储数据;如果删除或更改基础表,则查询视图将失败;视图是只读的,不能插入或装载数据
创建视图
create view view_name as select statement;查看视图定义
show create table view_name;删除视图
drop view_name;更改视图属性
alter view view_name set tblproperties ('comment' = 'This is a view');更改视图定义
alter view view_name as select statement;Hive侧视图(Lateral View)
select name,wps,gender_age.gender, gender_age.age,skill,score,depart,title
from employeelateral view explode(workplace) work_place as wpslateral view explode(skills_score) sks as skill, scorelateral view explode(depart_title) ga as depart, title;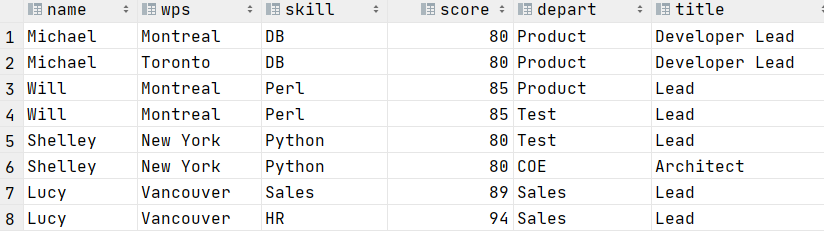
相关文章:

Hive建表高阶语句
CTAS -as select方式建表CREATE TABLE ctas_employee as SELECT * FROM employee;CTE (CTAS with Common Table Expression)CREATE TABLE cte_employee AS WITH r1 AS (SELECT name FROM r2 WHERE name Michael), r2 AS (SELECT name FROM employee WHERE gender Male), r3 …...

面向新时代,海泰方圆战略升级!“1465”隆重发布!
过去四年,海泰方圆“1344”战略一直在引领公司前行,搭建了非常坚实的战略框架基座,并推动全员在实践和行动中达成深度共识。 “1344”战略 1个定位,代表着当前机构用户的一组共性需求,密码安全数据治理信创工程。 3…...
带你感受一次JVM调优实战
本文分成两部分,先了解理论,然后再进行实战。 理论篇 1.1 调优目标 JVM调优的两大目标是: 提高应用程序的性能和吞吐量: 通过优化JVM的垃圾回收机制、调整线程池大小和优化代码,可以提高应用程序的性能和吞吐量。…...

ALG和STUN
目录 ALG 应用层网关讲解 Client1使用FTP主动模式建立FTP Client1使用FTP被动模式建立FTP STUN讲解 ALG 应用层网关讲解 用来替换应用层信息 Client1使用FTP主动模式建立FTP 主动模式:服务器收到客户端发来的请求FTP的地址和端口 服务器使用20端口直接向客户端建…...

原生HTML放大镜
该放大区域用背景图片放大 <!DOCTYPE html> <html lang"zh"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><meta http-equiv"X-UA-Compat…...

C++——模板
文章目录1 泛型编程2 函数模板2.1 函数模板概念2.2 函数模板格式2.3 函数模板的实例化2.3.1 隐式实例化2.3.1.1 定义2.3.1.2 代码演示2.3.1.3 运行结果2.3.1.4 缺点2.3.2 显式实例化2.3.2.1 格式2.3.2.2 代码演示2.3.2.3 运行结果2.4 模板参数的匹配原则2.4.12.4.22.4.33 类模板…...

Chapter2.1:线性表基础
该系列属于计算机基础系列中的《数据结构基础》子系列,参考书《数据结构考研复习指导》(王道论坛 组编),完整内容请阅读原书。 1.线性表的定义和基本操作 1.1 线性表的定义 线性表是具有相同数据类型的n(n≥0)n(n≥0)n(n≥0)个数据元素的有限序列&…...

Spring源码解析-Spring 循环依赖
Spring源码解析简图: Spring 如何解决循环依赖,⽹上的资料很多,但是感觉写得好的极少,特别是源码解读⽅⾯,我就⾃⼰单独出⼀ 篇,这篇⽂章绝对肝! 文章目录: 一. 基础知识 1.1 什么…...
从零开始学架构——架构设计的目的
软件架构的历史背景 软件架构真正流行是从20世纪90年代开始的,由于在Rational和Microsoft内部的相关活动,软件架构的概念开始越来越流行。 卡内基梅隆高校的玛丽肖(Mary Shaw)和戴维加兰 (David Garlan)对软件架构做了许多讨论,他们在 1994 年的一篇文章…...
)
Python 异步: 异步生成器(16)
动动发财的小手,点个赞吧! 生成器是 Python 的基本组成部分。生成器是一个至少有一个“yield”表达式的函数。它们是可以暂停和恢复的函数,就像协程一样。 实际上,Python 协程是 Python 生成器的扩展。Asyncio 允许我们开发异步生…...
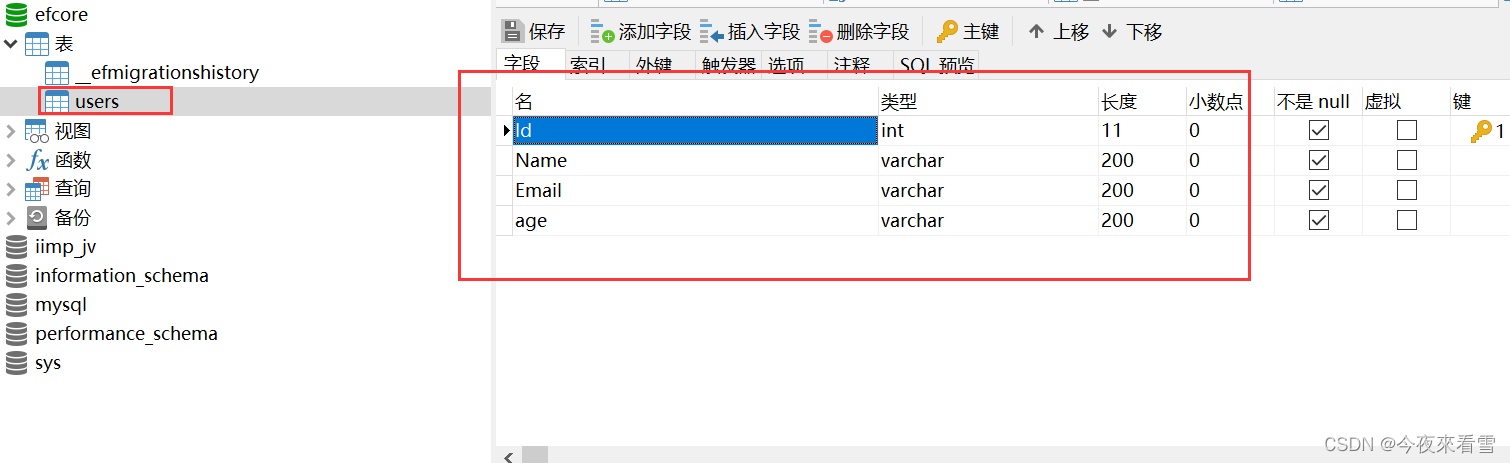
.net6 web api使用EF Core,根据model类自动生成表
1.安装EF Core和mysql数据库的nuget包 Microsoft.EntityFrameworkCore Pomelo.EntityFrameworkCore.MySql 2.创建models文件夹,在文件夹下创建实体类 public class Users{public int Id { get; set; }[Column(TypeName "varchar(200)"), Required]publ…...
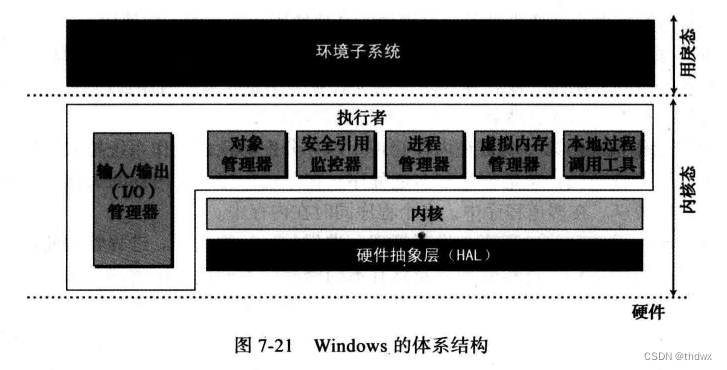
计算机科学导论笔记(五)
目录 七、操作系统 7.1 引言 7.1.1 操纵系统 7.1.2 自举过程 7.2 演化 7.3 组成部分 7.3.1 用户界面 7.3.2 内存管理器 7.3.3 进程管理器 7.3.4 设备管理器 7.3.5 文件管理器 7.4 操作系统 7.4.1 UNIX 7.4.2 Linux 7.4.3 Windows 七、操作系统 7.1 引言 计算机…...

通过命令打Java可执行jar包
文章目录1.背景2.操作步骤2.1. 准备好java源文件2.2 确认java源文件中是否有包名2.3 编译java文件2.4 初步打包2.5 解压jar包,得到MANIFEST.MF文件2.6 修改MANIFEST.MF文件2.7 再次打包3.验证4.打包参数参考5.参考文章1.背景 今天,无意中翻出了N年之前年…...
 接口和抽象类)
java基础系列(九) 接口和抽象类
一. 接口 简单的说,接口就是一种被规范的标准,只要符合这个标准都可以通用,接口的表现 在于对行为的抽象. 1.1 创建接口的格式 格式1: public interface 接口名 格式2: interface 接口名 1.2 在JDK1.8之后, 在接口中可以定义实现的方…...

Docker启动问题docker is starting…
环境window 10 家庭最新版直接上官网安装的 Docker DeskTop问题启动应用后setting打开一直转圈圈;主界面一直显示 docker is starting…解决方案3.1 先确定hyper-v是否开启搜hyper-v,点击启动或关闭Windows功能如下,选中Hyper-V服务3.2 进入任务管理期&a…...

Django/Vue实现在线考试系统-03-开发环境搭建-MySQL安装
1.概述 MySQL是一种关系型数据库管理系统,所使用的 SQL 语言是用于访问数据库的最常用标准化语言。MySQL 软件采用了双授权政策,分为社区版和商业版,由于其体积小、速度快、总体拥有成本低,尤其是开放源码这一特点,一般中小型和大型网站的开发都选择 MySQL 作为网站数据库…...
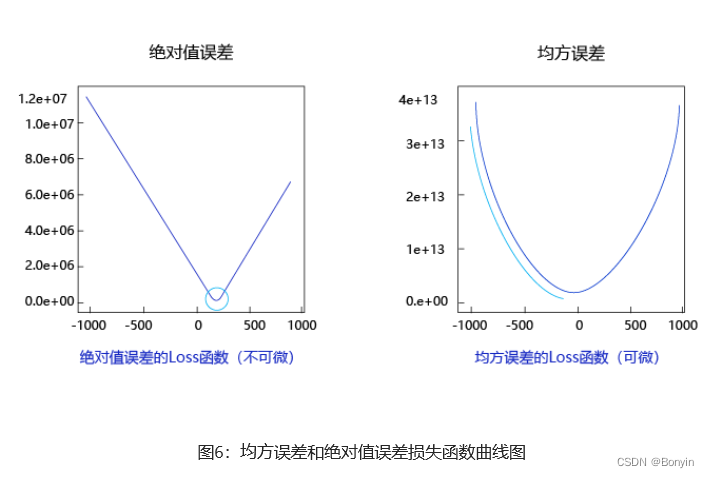
python实现波士顿房价预测
波士顿房价预测 目标 这是一个经典的机器学习回归场景,我们利用Python和numpy来实现神经网络。该数据集统计了房价受到13个特征因素的影响,如图1所示。 对于预测问题,可以根据预测输出的类型是连续的实数值,还是离散值ÿ…...

Pinia不酸,保甜
为什么是Pinia 怎么说呢,其实在过往的大部分项目里面,我并没有引入过状态管理相关的库来维护状态。因为大部分的业务项目相对来说比较独立,哪怕自身功能复杂的时候,可能也仅仅是通过技术栈自身的提供的状态管理能力来处理业务场景…...

uniapp生命周期
uniapp生命周期 uniapp生命周期不同于vue生命周期,uniapp生命周期分为: 应用生命周期 页面生命周期 组件生命周期 应用生命周期(官网) 注意 应用生命周期仅可在App.vue中监听,在其它页面监听无效。 onlaunch里进行页面跳转,如遇白…...
)
经典卷积模型回顾11—Xception实现图像分类(matlab)
Xception是一种深度卷积神经网络,它采用了分离卷积来实现深度神经网络的高准确性和高效率。Xception的名称来自“extreme inception”,意思是更加极致的Inception网络。 在传统的卷积神经网络中,每个卷积层都有若干个滤波器(即卷…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

对象回调初步研究
_OBJECT_TYPE结构分析 在介绍什么是对象回调前,首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例,用_OBJECT_TYPE这个结构来解析它,0x80处就是今天要介绍的回调链表,但是先不着急,先把目光…...

内窥镜检查中基于提示的息肉分割|文献速递-深度学习医疗AI最新文献
Title 题目 Prompt-based polyp segmentation during endoscopy 内窥镜检查中基于提示的息肉分割 01 文献速递介绍 以下是对这段英文内容的中文翻译: ### 胃肠道癌症的发病率呈上升趋势,且有年轻化倾向(Bray等人,2018&#x…...
