Cannot read properties of undefined (reading ‘init‘)报错

出现这个报错是印象项目没有引echarts包
npm i echarts 下包
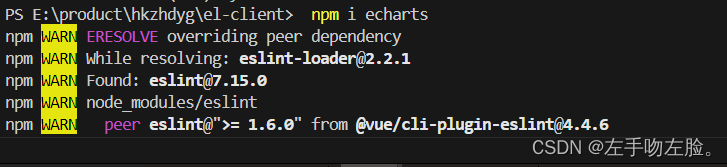
然后在main.js中引入
import echarts from 'echarts'
Vue.prototype.$echarts = echarts
如果还不行
import * as echarts from 'echarts';
更改一下引入方式
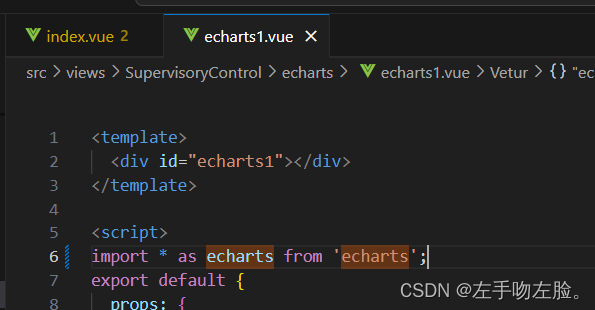
ok了
相关文章:

Cannot read properties of undefined (reading ‘init‘)报错
出现这个报错是印象项目没有引echarts包 npm i echarts 下包 然后在main.js中引入 import echarts from echarts Vue.prototype.$echarts echarts 如果还不行 import * as echarts from echarts; 更改一下引入方式 ok了...

golang html/template模板中使用自定义函数/方法的2种方法总结
在golang的html/template模板库中我们如果希望在视图文件中调用自定义的函数 或者方法可以通过以下2种方法实现: 1. 调用自定义函数 可通过将自定义的函数加入到 template.FuncMap中,然后再使用 template.New("xxx.html").Funcs(funcMap)来在…...

浅析vue3自定义指令
vue3中可以像下面这样使用自定义指令。 这里我们只是定义了一个vFoucs变量,vue怎么知道这是一个指令呢? 这是因为约定大于配置,vue3中有这样一个约定(截图来自官方文档): 注意这里说的是驼峰命令&#x…...
后仿真中的关于延时问题(延迟类型选择和脉冲控制)
目录 通过前面的文章提到,从物理特性角度出发,仿真中存在两种延时:惯性延时和传输延时。那么,实际仿真电路过程中,我们究竟选择的哪种模式呢? 一 指定传输延迟类型 传输延迟类型不是默认的延迟类型。我们需要显示指定它。 1.1 module-path delay VCS 仿真中添加如下三…...
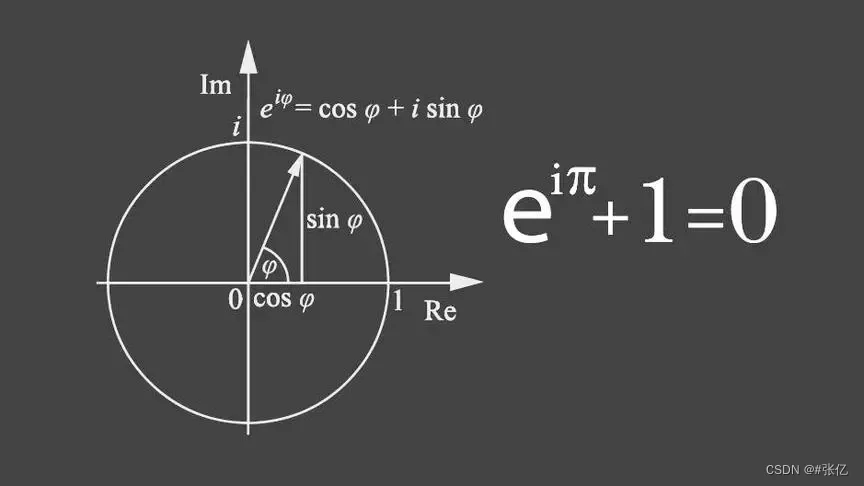
欧拉公式e^(ix)=(cos x+isin x)
啊,哈喽,小伙伴们大家好。我是#张亿,今天呐,学的是欧拉公式 在不同的学科中有着不同的含义和应用。在复变函数中,欧拉公式表述为e^(ix)(cos xisin x),其中e是自然对数的底,i是虚数单位&#x…...

Android 获取已安装应用、包名、应用名、版本号、版本名
1、相关代码 List<ApplicationInfo> installedApps getPackageManager().getInstalledApplications(0);for (ApplicationInfo appInfo : installedApps) {CharSequence getAppName getPackageManager().getApplicationLabel(appInfo);String appNamegetAppName.toStrin…...
2024数学建模深圳杯B题成品论文43页word+完整可视化结果图+可执行代码
【无水印word】2024深圳杯B题成品论文43页(附带1-4小问完整py解题代码思路)https://www.jdmm.cc/file/2710664 批量工件并行切割下料优化研究 摘 要 本研究针对批量工件并行切割下料问题展开了深入的探讨与分析。通过建立数学模型和运用优化算法&…...
达梦(DM) SQL查询及联合查询
达梦DM SQL查询及联合查询 查询结果排序多表联合查询 这里继续讲解DM数据库的Sql查询操作 查询结果排序 为提高查询结果可读性,我们可以对查询结果按照一定顺序排列,或者也可以将列名替换成数字,例如 ORDER BY 1 DESC,意思是按第…...
【重生之我在学Android】WorkManager (章一)
相关文章 【重生之我在学Android原生】ContentProvider(Java) 【重生之我在学Android原生】Media3 【重生之我在学Android】WorkManager (章一) 前言 官方文档 官方推荐 - 前台服务、后台服务都可以使用WorkManger来实现 案例 语言:JA…...
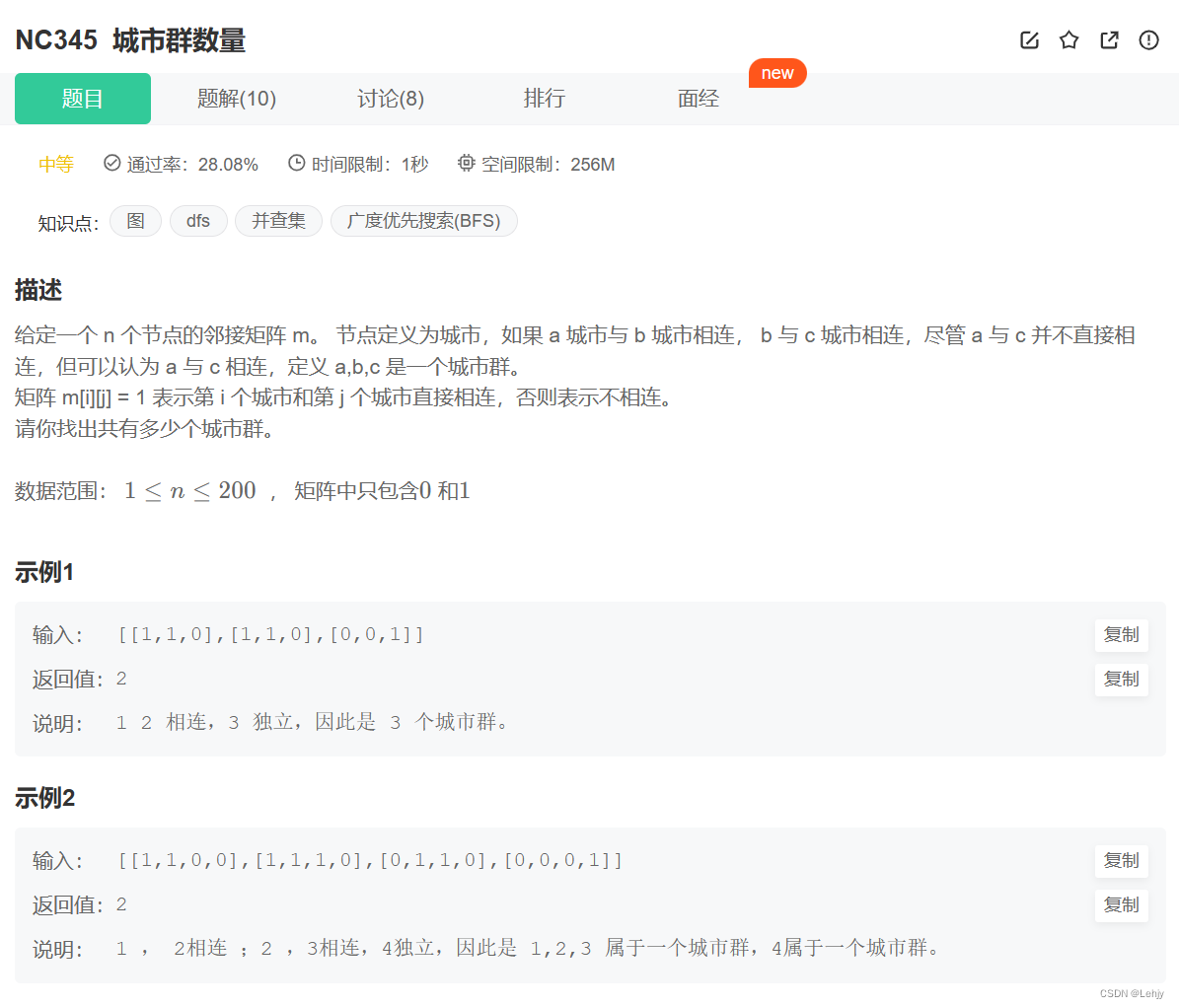
【强训笔记】day23
NO.1 思路:直接计算结果,先计算怪物可以抗几次攻击,再计算勇士受到的伤害,如果勇士的攻击力大于等于怪物的血量,那么就可以击杀无数只,如果勇士的血量正好是受到攻击的整数倍,那么击杀的怪物数…...

C语言-STM32:介绍PWM,并使用PWM实现呼吸灯
1、什么是PWM PWM,全称为Pulse Width Modulation,中文名为脉冲宽度调制。这是一种模拟控制技术,通过改变脉冲信号的宽度来表征一个连续变量的平均值,通常用于对模拟信号的数字化控制,特别是在功率转换和信号处理中非常…...

SpringBean详解
文章目录 概述Spring获取Bean的流程依赖注入bean的作用域Spring 中的 Bean 是线程安全的吗Spring如何处理线程并发问题bean 的自动装配和方式Resource和Autowired的区别bean的自动装配bean的生命周期BeanFactoryBeanFactory 常用的实现类有哪些BeanFactory与FactoryBean的不同A…...

hive获取这周五到下周四的区间,周一到周日的区间
-- 获取每个日期所在周期的开始和结束时间 SELECTcreated_date AS date_in_period,CASEWHEN date_format(created_date, u) < 5 THEN date_sub(created_date, cast(date_format(created_date, u) AS INT) 2)ELSE date_sub(created_date, cast(date_format(created_date, u)…...
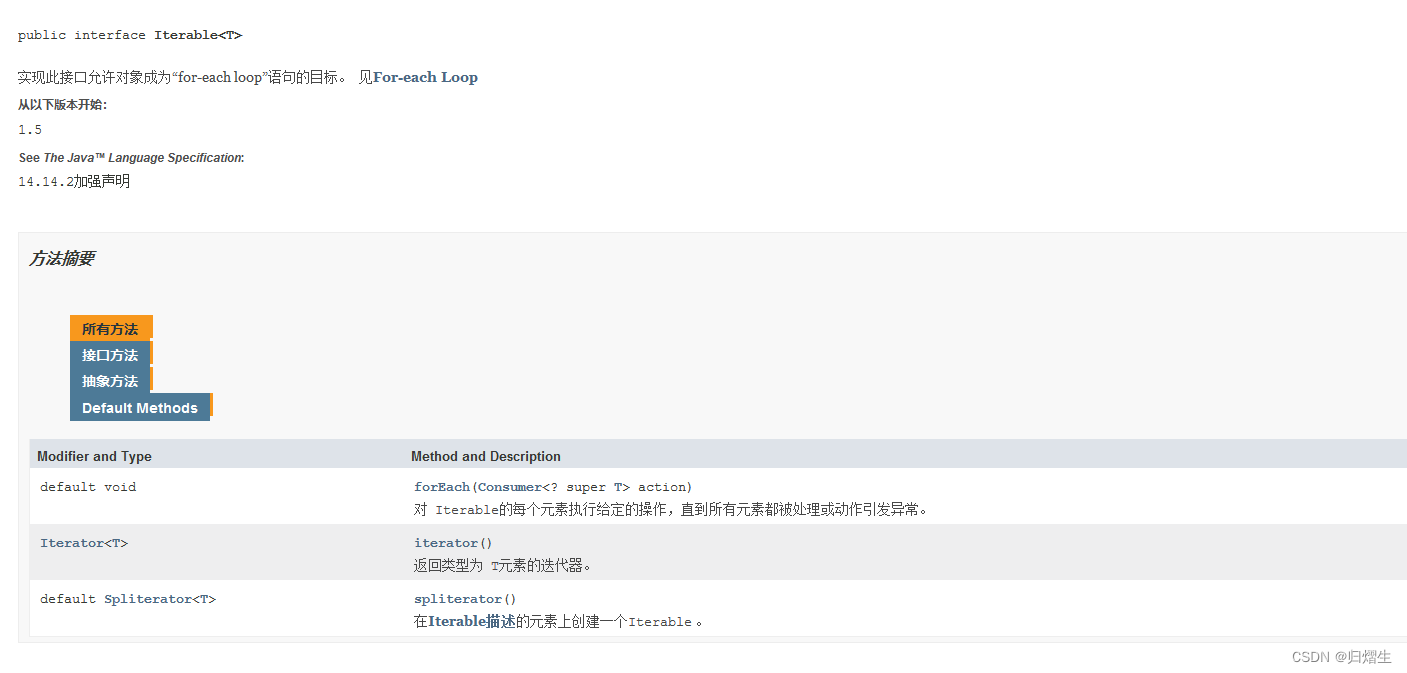
Iterable与Iterator
Iterator public interface Iterator<E> {} terator是一个接口,它是集合的迭代器。集合可以通过Iterator去遍历集合中的元素。Iterator提供的API接口如下: forEachRemaining(Consumer<? super E> action):为每个剩余元素执行给…...

免费Premiere模板,几何图形元素动画视频幻灯片模板素材下载
Premiere Pro模板,几何图形元素动画视频幻灯片模板 ,组织良好,易于自定义。包括PDF教程。 项目特点: 使用Adobe Premiere Pro 2021及以上版本。 19201080全高清。 不需要插件。 包括帮助视频。 免费下载:https://prmu…...

数据结构与算法学习笔记九---循环队列的表示和实现(C++)
目录 前言 1.为什么要使用循环队列 2.队列的顺序存储方式的实现 1.定义 2.队列初始化 3.销毁 4.清空队列 5.队列是否为空 6.队列长度 7.队头 8.入队 9.出队 10.遍历队列 11.完整代码 3.参考资料 前言 这篇文章介绍循环队列的表示和用法。 1.为什么要使用循环队…...

Mysql获取当前时间
1、今天开始时间和结束时间 SELECT DATE_FORMAT(NOW(),’%Y-%m-%d 00:00:00’) AS ‘今天开始’; SELECT DATE_FORMAT(NOW(),’%Y-%m-%d 23:59:59’) AS ‘今天结束’;2、昨天的开始时间和结束时间 SELECT DATE_FORMAT( DATE_SUB(CURDATE(), INTERVAL 1 DAY), ‘%Y-%m-%d 00:…...

计算机服务器中了locked勒索病毒怎么解决,locked勒索病毒解密恢复工具
在网络技术飞速发展的时代,通过网络开展各项工作业务成为众多企业的首选,网络也为企业的生产运营提供了极大便利,大大提升了企业办公效率,但是利用网络避免不了网络威胁的存在,数据安全问题一直是企业关心的主要话题。…...

基于springboot实现的在线动漫信息平台
开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7(一定要5.7版本) 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven…...
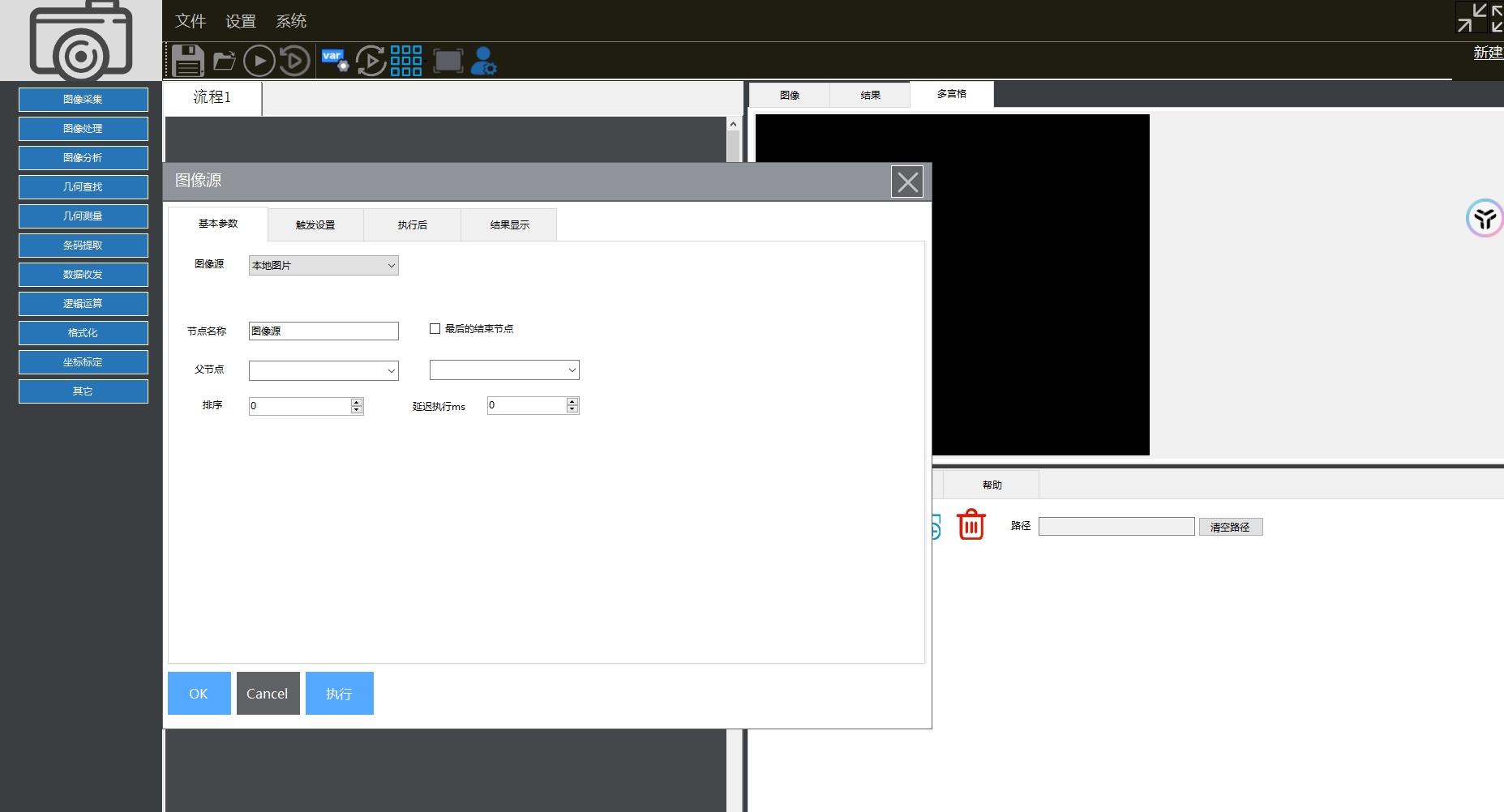
C# Winform+Halcon结合标准视觉工具
介绍 winform与halcon结合标准化工具实例 软件架构 软件架构说明 基于NET6 WINFORMHALCON 实现标准化视觉检测工具 集成相机通讯 集成PLC通讯 TCP等常见通讯 支持常见halcon算子 图形采集blob分析高精度匹配颜色提取找几何体二维码提取OCR识别等等 。。。 安装教程 …...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...
