【二叉树】(三)二叉树的基础修改构造及属性求解2
(二)二叉树的基础修改构造及属性求解2
- 二叉树的所有路径
- 思路
- 递归法
- 迭代法
- 左叶子之和
- 递归法
- 迭代法
- 找树左下角的值
- 递归法
- 迭代法
- 路径总和
- 从中序与后序遍历序列构造二叉树
- 最大二叉树
- 合并二叉树
二叉树的所有路径
力扣原题链接:257. 二叉树的所有路径
给定一个二叉树,返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。
示例:

思路
- 这道题目要求从根节点到叶子的路径,所以需要前序遍历,这样才方便让父节点指向孩子节点,找到对应的路径。
- 在这道题目中将第一次涉及到回溯,因为我们要把路径记录下来,需要回溯来回退一个路径再进入另一个路径。
前序遍历以及回溯的过程如图:

由于回溯算法将在下个章节重点学习,这里先提前了解一下即可,核心还在于前序的递归遍历的设计。
递归法
1. 递归函数参数以及返回值
要传入根节点,记录每一条路径的path,和存放结果集的result,这里递归不需要返回值,代码如下:
void traversal(TreeNode* node, vector<int>&path, vector<string>& res)
2. 确定递归终止条件
在写递归的时候都习惯了这么写:
if (cur == NULL) {终止处理逻辑
}
但是本题的终止条件这样写会很麻烦,因为本题要找到叶子节点,就开始结束的处理逻辑了(把路径放进result里)。
那什么时候算是找到叶子节点? 是当 cur不为空,其左右孩子都为空的时候,就找到叶子节点。
所以本题的终止条件是:
//访问到子节点
if(node->left == NULL && node->right == NULL)
{//终止处理逻辑//把path内的数据封装成string格式,并添加至res
}
这里我们先使用vector结构的path容器来记录路径,那么终止处理逻辑如下:
//访问到子节点
if(node->left == NULL && node->right == NULL)
{string buf;for(int i = 0; i < path.size()-1; i++){buf += to_string(path[i]);buf += "->";}buf += to_string(path[path.size() - 1]);res.push_back(buf);return;
}
3. 确定单层递归逻辑
因为是前序遍历,需要先处理中间节点,中间节点就是我们要记录路径上的节点,先放进path中。
//中 先把叶子节点的值放入path
path.push_back(node->val);
回溯和递归是一一对应的,有一个递归,就要有一个回溯。所以回溯要和递归永远在一起,世界上最遥远的距离是你在花括号里,而我在花括号外!
//左
if(node->left)
{traversal(node->left, path, res);path.pop_back(); //回溯
}//右
if(node->right)
{traversal(node->right, path, res);path.pop_back(); //回溯
}
那么本题整体代码如下:
class Solution {
public:void traversal(TreeNode* node, vector<int>&path, vector<string>& res){//中 先把叶子节点的值放入pathpath.push_back(node->val);//访问到子节点if(node->left == NULL && node->right == NULL){string buf;for(int i = 0; i < path.size()-1; i++){buf += to_string(path[i]);buf += "->";}buf += to_string(path[path.size() - 1]);res.push_back(buf);return;}//左if(node->left){traversal(node->left, path, res);path.pop_back(); //回溯}//右if(node->right){traversal(node->right, path, res);path.pop_back(); //回溯}}vector<string> binaryTreePaths(TreeNode* root) {vector<int> path;vector<string> res;if(root == NULL)return res;traversal(root,path,res);return res;}
};
迭代法
至于非递归的方式,我们可以依然可以使用前序遍历的迭代方式来模拟遍历路径的过程,这里除了模拟递归需要一个栈,同时还需要一个栈来存放对应的遍历路径。
左叶子之和
力扣原题链接:404. 左叶子之和
计算给定二叉树的所有左叶子之和。
示例:

左叶子的明确定义:节点A的左孩子不为空,且左孩子的左右孩子都为空(说明是叶子节点),那么A节点的左孩子为左叶子节点
那么判断当前节点是不是左叶子是无法判断的,必须要通过节点的父节点来判断其左孩子是不是左叶子。
如果该节点的左节点不为空,该节点的左节点的左节点为空,该节点的左节点的右节点为空,则找到了一个左叶子,判断代码如下:
if (node->left != NULL && node->left->left == NULL && node->left->right == NULL) {左叶子节点处理逻辑
}
递归法
1. 确定递归函数的参数和返回值
判断一个树的左叶子节点之和,那么一定要传入树的根节点,递归函数的返回值为数值之和,所以为int。
int traversal(TreeNode* node)
2. 确定终止条件
- 如果遍历到空节点,那么左叶子值一定是0
if(node == NULL) //根节点为空 返回return 0; - 注意,只有当前遍历的节点是父节点,才能判断其子节点是不是左叶子。 所以如果当前遍历的节点是叶子节点,那其左叶子也必定是0,那么终止条件为:
if(node == NULL) //根节点为空 返回return 0; if(node->left == NULL && node->right == NULL) //叶子节点return 0;
3. 确定单层递归的逻辑
当遇到左叶子节点的时候,记录数值,然后通过递归求取左子树左叶子之和,和 右子树左叶子之和,相加便是整个树的左叶子之和
//递归遍历 左子树
int leftSum = sumOfLeftLeaves(node->left);
//存在左叶子
if(node->left && node->left->left == NULL && node->left->right == NULL)leftSum = node->left->val;//递归遍历 右子树
int rightSum = sumOfLeftLeaves(node->right);return leftSum + rightSum; //中
整体递归代码如下:
class Solution {
public:int traversal(TreeNode* node){int sum = 0;if(node == NULL) //根节点为空 返回return 0;if(node->left == NULL && node->right == NULL) //叶子节点return 0;//递归遍历 左子树int leftSum = sumOfLeftLeaves(node->left); //存在左叶子if(node->left && node->left->left == NULL && node->left->right == NULL)leftSum = node->left->val;//递归遍历 右子树int rightSum = sumOfLeftLeaves(node->right);return leftSum + rightSum; //中}int sumOfLeftLeaves(TreeNode* root) {int sum = traversal(root);return sum; }
};
迭代法
找树左下角的值
力扣原题链接:513. 找树左下角的值
本题要找出树的最后一行的最左边的值,显然此题用迭代法层序遍历最适合不过,其实用迭代法比递归法更简单一点点,至于迭代法比较简单,记录每层最左边一个元素后,最后返回即可,因此这里还是用递归法进行详细展开,迭代法只记录最后的实现代码
递归法
- 如果使用递归法,判断是最后一行其实就是深度最大的叶子节点一定是最后一行。
- 如何找最左边的呢?可以使用前序遍历(当然中序,后序都可以,因为本题没有 中间节点的处理逻辑,只要左优先就行),保证优先左边搜索,然后记录深度最大的叶子节点,此时就是树的最后一行最左边的值。
递归三部曲:
1. 确定递归函数的参数和返回值
- 参数必须有要遍历的树的根节点,还有就是一个int型的变量用来记录最长深度。 这里就不需要返回值了,所以递归函数的返回类型为
void。 - 本题还需要类里的两个全局变量,
maxDepth用来记录最大深度,res记录最大深度最左节点的数值。//递归函数 void traversal(TreeNode* node, int depth)
2. 确定终止条件
当遇到叶子节点的时候,就需要统计一下最大的深度了,所以需要遇到叶子节点来更新最大深度,代码如下:
//找到叶子节点
if(node->left == NULL && node->right == NULL)
{if(depth > maxDepth){maxDepth = depth;res = node->val;}
}
3. 确定单层递归的逻辑
在找最大深度的时候,递归的过程中依然要使用回溯,代码如下:
if(node->left) //左
{depth++; //加入左节点 深度+1traversal(node->left, depth);depth--; //回溯
}if(node->right) //右
{depth++; //加入右节点 深度+1traversal(node->right, depth);depth--; //回溯
}
完整代码如下:
class Solution {
public://递归法int maxDepth = -1;int res;//递归函数void traversal(TreeNode* node, int depth){//找到叶子节点if(node->left == NULL && node->right == NULL){if(depth > maxDepth){maxDepth = depth;res = node->val;} }//中 不需要处理if(node->left) //左{depth++; //加入左节点 深度+1traversal(node->left, depth);depth--; //回溯}if(node->right) //右{depth++; //加入右节点 深度+1traversal(node->right, depth);depth--; //回溯}}int findBottomLeftValue(TreeNode* root) {traversal(root,0);return res;}
}
迭代法
迭代法的核心即覆盖记录每层最左边元素的值,最后返回记录的值即可。
class Solution {
public://层序遍历int findBottomLeftValue(TreeNode* root) {if(root == NULL)return 0;int size;queue<TreeNode*> que;int ret; //记录每层最左边的节点值que.push(root);while(!que.empty()){//获取每层的节点个数size = que.size();ret = que.front()->val;while(size--){TreeNode* node = que.front();que.pop();if(node->left)que.push(node->left);if(node->right)que.push(node->right);}size = que.size(); //跟新}return ret;}
};
路径总和
力扣原题链接:112. 路径总和
给定二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。

输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
1. 确定递归函数的参数和返回类型
参数: 需要二叉树的根节点,还需要一个计数器,这个计数器用来计算二叉树的一条边之和是否正好是目标和,计数器为int型。
返回值: 本题是找一条符合条件的路径,所以递归函数需要返回值,从下图可以看出,遍历的路线,并不要遍历整棵树,所以递归函数需要返回值,可以用bool类型表示。

所以代码如下:
bool traversal(TreeNode* node, int count)
2. 确定终止条件
- 不要去累加然后判断是否等于目标和,那么代码比较麻烦,可以用递减,让计数器count初始为目标和,然后每次减去遍历路径节点上的数值。
- 如果最后count == 0,同时到了叶子节点的话,说明找到了目标和。
- 如果遍历到了叶子节点,count不为0,就是没找到。
递归终止条件代码如下:
//遇到可行路径的叶子节点
if(node->left == NULL && node->right == NULL && count == 0)return true; //一路减下来 是目标路径
//其他叶子节点
if(node->left == NULL && node->right == NULL)return false;
3. 确定单层递归的逻辑
- 因为终止条件是判断叶子节点,所以递归的过程中就不要让空节点进入递归了。
- 递归函数是有返回值的,如果递归函数返回
true,说明找到了合适的路径,应该立刻返回。
代码如下:
//向左遍历
if(node->left)
{count -= node->left->val;bool ret = traversal(node->left,count);if(ret) //如果存在 一路返回return true;count += node->left->val; //回溯count
}
//向右遍历
if(node->right)
{count -= node->right->val;bool ret = traversal(node->right,count);if(ret) //如果存在 一路返回return true;count += node->right->val; //回溯count
}
return false;
整体代码如下:
class Solution {
public://递归函数bool traversal(TreeNode* node, int count){//遇到可行路径的叶子节点if(node->left == NULL && node->right == NULL && count == 0)return true; //一路减下来 是目标路径//其他叶子节点if(node->left == NULL && node->right == NULL)return false;//向左遍历if(node->left){count -= node->left->val;bool ret = traversal(node->left,count);if(ret) //如果存在 一路返回return true;count += node->left->val; //回溯count }//向右遍历if(node->right){count -= node->right->val;bool ret = traversal(node->right,count);if(ret) //如果存在 一路返回return true;count += node->right->val; //回溯count }return false;}bool hasPathSum(TreeNode* root, int targetSum) {if(root == NULL)return false;int res = traversal(root, targetSum - root->val);return res;}
};
从中序与后序遍历序列构造二叉树
力扣原题链接:106. 从中序与后序遍历序列构造二叉树
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
输入:
- 中序遍历:inorder = [9,3,15,20,7]
- 后序遍历:postorder = [9,15,7,20,3],返回如下二叉树:

思路
以 后序数组的最后一个元素为切割点,先切中序数组,根据中序数组,反过来再切后序数组。一层一层切下去,每次后序数组最后一个元素就是节点元素。
流程如图:

那么代码应该怎么写呢?
说到一层一层切割,就应该想到了递归。
来看一下一共分几步:
-
第一步:如果数组大小为零的话,说明是空节点了。
-
第二步:如果不为空,那么取后序数组最后一个元素作为节点元素。
-
第三步:找到后序数组最后一个元素在中序数组的位置,作为切割点
-
第四步:切割中序数组,切成中序左数组和中序右数组 (顺序别搞反了,一定是先切中序数组)
-
第五步:切割后序数组,切成后序左数组和后序右数组
-
第六步:递归处理左区间和右区间
根据思路写出每一步的代码,完整代码如下,但要注意以下几个点:
- 切割标准的定义:这里使用的是左闭右开
- 切割点在后序数组的最后一个元素,就是用这个元素来切割中序数组的,所以必要先切割中序数组
- 切割后续数组时,有一个很重的点,就是中序数组大小一定是和后序数组的大小相同的,后序数组就可以按照左中序数组的大小来切割,切成左后序数组和右后序数组。
- 代码写出来一定是各种问题,所以一定要加日志来调试,看看是不是按照自己思路来切割的,不要大脑模拟,那样越想越糊涂。
class Solution {
public:TreeNode* traversal(vector<int>& inorder, vector<int>& postorder){//1. 后续数组为空 返回if(postorder.empty())return NULL;//2. 获取根节点的值(后续数组中的最后一个值)int val = postorder[postorder.size() - 1];TreeNode* root = new TreeNode(val);if(postorder.size() == 1) //只有1个叶子节点return root;//3. 找切割点 计算根节点的值在中序数组中的下标 int idx; //根节点值在中序数组中的下标for(idx = 0; idx < postorder.size(); idx++){if(inorder[idx] == val)break; }//要确定顺序得看后序,因为中序不知道中间节点在哪//4. 切割中序数组vector<int> inleft; //左中序 [0,idx)vector<int> inright; //右中序 [idx+1,size)for(int i = 0; i < idx; i++) inleft.push_back(inorder[i]); for(int i = idx+1; i < inorder.size(); i++) inright.push_back(inorder[i]);//5. 切割后续数组vector<int> postleft; //左后序 [0,size)vector<int> postright; //右后序 [inleft.size, size)for(int i = 0; i < inleft.size(); i++) postleft.push_back(postorder[i]);//左侧数组长度是一样的for(int i = inleft.size(); i < postorder.size() - 1; i++) postright.push_back(postorder[i]);/*cout << "------------debug------------------" << endl;cout << "------------inorder------------------"<< endl;for(int i = 0; i < inorder.size();i++)cout << inorder[i] << " ";cout << endl;cout << "------------postorder------------------"<< endl;for(int i = 0; i < postorder.size();i++)cout << postorder[i] << " ";cout << endl;cout << "val = " << val << endl;cout << "idx = " << idx << endl;cout << "------------inleft------------------"<< endl;for(int i = 0; i < inleft.size();i++)cout << inleft[i] << " ";cout << endl;cout << "------------inright------------------"<< endl;for(int i = 0; i < inright.size();i++)cout << inright[i] << " ";cout << endl;cout << "------------postleft------------------"<< endl;for(int i = 0; i < postleft.size();i++)cout << postleft[i] << " ";cout << endl;cout << "------------postright------------------"<< endl;for(int i = 0; i < postright.size();i++)cout << postright[i] << " ";cout << endl;
*/ //6. 递归处理左区间、右区间root->left = traversal(inleft,postleft);root->right = traversal(inright,postright);return root;}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {if(inorder.size() == 0 || postorder.size() == 0)return NULL;return traversal(inorder, postorder);}
};
最大二叉树
力扣原题链接:654. 最大二叉树
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
-
创建一个根节点,其值为 nums 中的最大值。
-
递归地在最大值 左边 的 子数组前缀上 构建左子树。
-
递归地在最大值 右边 的 子数组后缀上 构建右子树。

如果对于上一题有较好的理解与设计的话,那么本题相对比较简单,本题思路与上一题完全相似,且更简单。
思路
最大二叉树的构建过程如下:

1. 确定递归函数的参数和返回值
参数传入的是存放元素的数组,返回该数组构造的二叉树的头结点,返回类型是指向节点的指针。
代码如下:
TreeNode* traversal(vector<int>& nums)
2. 确定终止条件
那么当递归遍历的时候,如果传入的数组大小为1,说明遍历到了叶子节点了。
那么应该定义一个新的节点,并把这个数组的数值赋给新的节点,然后返回这个节点。 这表示一个数组大小是1的时候,构造了一个新的节点,并返回。
代码如下:
TreeNode* node = new TreeNode(0);
if (nums.size() == 1) {node->val = nums[0];return node;
}
3. 确定单层递归的逻辑
这里有四步工作
-
先要找到数组中最大的值和对应的下标, 最大的值构造根节点,下标用来下一步分割数组。
int maxValue = *max_element(nums.begin(),nums.end()); int maxPosition = max_element(nums.begin(),nums.end()) - nums.begin(); -
最大值所在的下标左区间 构造左子树
vector<int> leftNums; //[0,pos) for(int i = 0; i < maxPosition; i++)leftNums.push_back(nums[i]); -
最大值所在的下标右区间 构造右子树
vector<int> rightNums; //[Pos+1,size) for(int i = maxPosition + 1; i < nums.size(); i++)rightNums.push_back(nums[i]); -
递归处理左右数组
//4. 递归处理左右区间 root->left = traversal(leftNums); root->right = traversal(rightNums);return root;
完整版本代码:
class Solution {
public://做完106 再独立做这题 显得轻而易举 对比学习TreeNode* traversal(vector<int>& nums) {//1. 数组为空 返回if(nums.size() == 0)return NULL;//2. 获取最大值与最大值的下标int maxValue = *max_element(nums.begin(),nums.end());int maxPosition = max_element(nums.begin(),nums.end()) - nums.begin();TreeNode* root = new TreeNode(maxValue);//如果只有一个节点if(nums.size() == 1)return root;//3. 分割数组 形成左数组与右数组vector<int> leftNums; //[0,pos)vector<int> rightNums; //[Pos+1,size)for(int i = 0; i < maxPosition; i++)leftNums.push_back(nums[i]);for(int i = maxPosition + 1; i < nums.size(); i++)rightNums.push_back(nums[i]);//4. 递归处理左右区间root->left = traversal(leftNums);root->right = traversal(rightNums);return root;}TreeNode* constructMaximumBinaryTree(vector<int>& nums) {if(nums.size() == 0)return NULL;return traversal(nums);}
};
合并二叉树
力扣原题链接:617. 合并二叉树
给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点。
示例1:

示例2:

思路
- 其实和遍历一个树逻辑是一样的,只不过传入两个树的节点,同时操作。
- 本题使用哪种遍历都是可以的!
我们下面以前序遍历为例。
动画如下:

那么我们来按照递归三部曲来解决:
1. 确定递归函数的参数和返回值:
首先要合入两个二叉树,那么参数至少是要传入两个二叉树的根节点,返回值就是合并之后二叉树的根节点,代码如下:
TreeNode* traversal(TreeNode* root1, TreeNode* root2)
2. 确定终止条件:
因为是传入了两个树,那么就有两个树遍历的节点t1 和 t2,如果t1 == NULL 了,两个树合并就应该是 t2 了
//终止条件
if(root1 == NULL)return root2;
if(root2 == NULL)return root1;
3. 确定单层递归的逻辑:
这里重复利用一下t1这个树,t1就是合并之后树的根节点(就是修改了原来树的结构)。
-
那么单层递归中,就要把两棵树的元素加到一起。
-
接下来t1 的左子树是:合并 t1左子树 t2左子树之后的左子树。
-
t1 的右子树:是合并 t1右子树 t2右子树之后的右子树。
最终t1就是合并之后的根节点,代码如下:
root1->val += root2->val; //中
root1->left = traversal(root1->left, root2->left); //左
root1->right = traversal(root1->right, root2->right); //右return root1;
完整代码如下:
class Solution {
public:TreeNode* traversal(TreeNode* root1, TreeNode* root2){//终止条件if(root1 == NULL)return root2;if(root2 == NULL)return root1;root1->val += root2->val; //中root1->left = traversal(root1->left, root2->left); //左root1->right = traversal(root1->right, root2->right); //右return root1;}TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {return traversal(root1, root2);}
};
相关文章:

【二叉树】(三)二叉树的基础修改构造及属性求解2
(二)二叉树的基础修改构造及属性求解2 二叉树的所有路径思路递归法迭代法 左叶子之和递归法迭代法 找树左下角的值递归法迭代法 路径总和从中序与后序遍历序列构造二叉树最大二叉树合并二叉树 二叉树的所有路径 力扣原题链接:257. 二叉树的所…...
PyCharm2024安装教程
PyCharm是一款功能强大的Python集成开发环境(IDE),它提供了许多工具和功能来帮助开发者编写、调试和测试Python代码。以下是使用PyCharm的基本步骤: 安装PyCharm:首先,你需要从JetBrains官方网站下载并安装…...

JavaScript基础知识强化:变量提升、作用域逻辑及TDZ的全面解析
🔥 个人主页:空白诗 文章目录 ⭐️ 引言🎯 变量提升(Hoisting)👻 暂时性死区(Temporal Dead Zone, TDZ)解释📦 var声明🔒 let与const声明📖 函数声明 与 函数表达式函数声…...
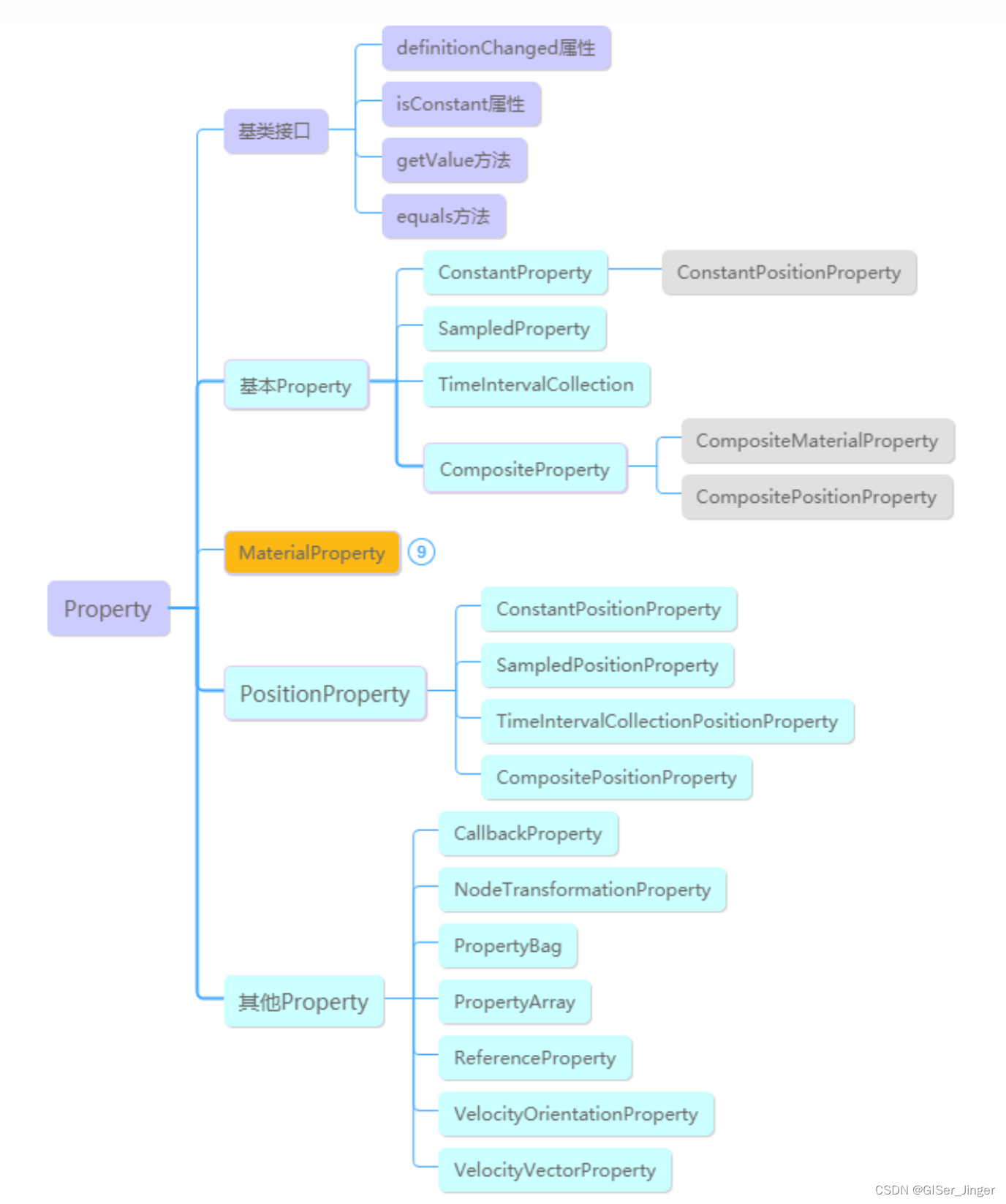
[Cesium]Cesium基础学习——Primitive
Cesium开发高级篇 | 01空间数据可视化之Primitive - 知乎 Primitive由两部分组成:几何体(Geometry)和外观(Appearance)。几何体定义了几何类型、位置和颜色,例如三角形、多边形、折线、点、标签等ÿ…...

java相等忽略音调
来自百度,亲测可用 java相等忽略音调 在Java中,如果你想比较两个字符串而忽略它们的音调符号,你可以使用java.text.Collator类来进行区域敏感的字符串比较。Collator类提供了根据特定区域的规则进行字符串比较的能力,可以设置忽略音调的选项…...

自养号测评实战指南:Shopee、Lazada销量翻倍不再是难题
对于速卖通、亚马逊、eBay、敦煌网、SHEIN、Lazada、虾皮等平台的卖家而言,提高店铺流量并转化为实际销量是共同追求的目标。在这个过程中,自养号进行产品测评显得尤为重要。通过精心策划和执行的测评活动,卖家不仅能够显著增加产品的销量&am…...
)
【Java开发面试系列】JVM相关面试题(精选)
【Java开发面试系列】JVM相关面试题(精选) 文章目录 【Java开发面试系列】JVM相关面试题(精选)前言一、JVM组成二、类加载器三、垃圾回收四、JVM实践(调优) 🌈你好呀!我是 山顶风景独…...

解决Win11下SVN状态图标显示不出来
我们正常SVN在Windows资源管理器都是有显示状态图标的, 如果不显示状态图标,可能你的注册表的配置被顶下去了,我们查看一下注册表 运行CMD > regedit 打开注册表编辑器 然后打开这个路径:计算机\HKEY_LOCAL_MACHINE\SOFTWARE…...

代码随想录训练营第四十天 | 343. 整数拆分、96.不同的二叉搜索树
343. 整数拆分 题目链接:. - 力扣(LeetCode) 文档讲解:代码随想录 视频讲解:动态规划,本题关键在于理解递推公式!| LeetCode:343. 整数拆分_哔哩哔哩_bilibili 状态:未通…...

python爬取数据并将数据写入execl表中
文章目录 概要 概要 提示:python爬取数据并将数据写入execl表中,仅供学习使用,代码是很久前的,可能执行不通,自行参考学习。 # -*- coding: utf-8 -*- import datetime # 日期库 import requests # 进行网络请求 im…...

Linux动静态库
Linux动静态库 1.动静态库介绍 在程序翻译的链接阶段,其实就是把一堆.o文件链接在一起形成.exe文件。如果一个程序中需要链接很多个.o文件,那么这些.o文件就需要被打包才方便管理,**库文件本质就是把.o文件打包。**库文件是一种提高开发效率…...
)
线程与进程___(一)
1、线程 Thread 类创建得线程为前台线程,线程池中的为后台线程,,,Main方法结束后,前台线程仍然运行,直到完成,而后台线程立刻结束。 调用线程时候不会立刻进入 Running 状态, 而是…...

Google IO 2024有哪些看点呢?
有了 24 小时前 OpenAI 用 GPT-4o 带来的炸场之后,今年的 Google I/O 还未开始,似乎就被架在了一个相当尴尬的地位,即使每个人都知道 Google 将发布足够多的新 AI 内容,但有了 GPT-4o 的珠玉在前,即使是 Google 也不得…...

纯血鸿蒙APP实战开发——Navigation页面跳转对象传递案例
介绍 本示例主要介绍在使用Navigation实现页面跳转时,如何在跳转页面得到转入页面传的类对象的方法。实现过程中使用了第三方插件class-transformer,传递对象经过该插件的plainToClass方法转换后可以直接调用对象的方法, 效果图预览 使用说…...

Windows C++ 读取、修改配置文件.ini
目录 一、INI文件基础介绍 二、GetPrivateProfileString和WritePrivateProfileString 解释: 一、INI文件基础介绍 INI文件(初始化文件)是一种简单的文本文件,用于存储程序的配置设置。它们通常用于Windows操作系统环境中&#x…...
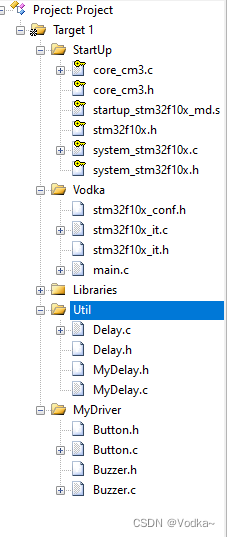
物联网D3——按键控制LED、光敏传感蜂鸣器
按键控制LED 按键抖动,电平发生变化,可用延时函数抵消按键抖动对系统的影响 传感器电路图 按键电路图 c语言对应类型 “_t”后缀表示使用typedef重命名的数据类型 枚举类型 #include<iostream> using namespace std; //定义枚举类型 typedef enu…...
Spring初学入门(跟学笔记)
一、Spring概述 Spring是一款主流的Java EE轻量级开源框架。 Spring的核心模块:IoC(控制反转,指把创建对象过程交给Spring管理 )、AOP(面向切面编程,在不修改源代码的基础上增强代码功能) 二、…...
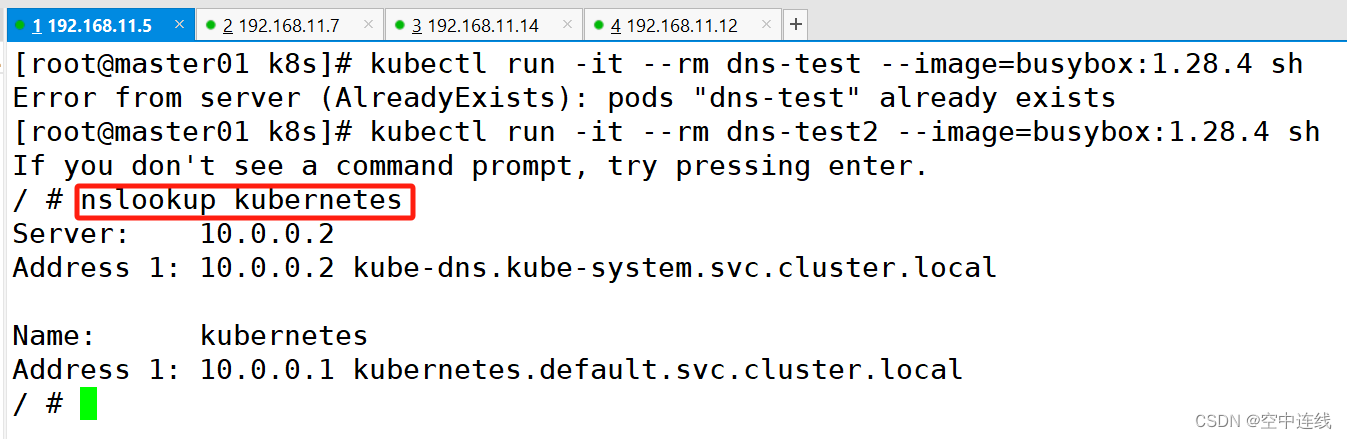
二进制部署k8s---下篇
一 master02 节点部署 1 先在master01 添加映射master02 对master02进行环境初始化 3 从 master01 节点上拷贝证书文件、各master组件的配置文件和服务管理文件到 master02 节点 scp -r /opt/etcd/ root192.168.11.12:/opt/ scp -r /opt/kubernetes/ root192.168.11.12:/opt…...

基于Sentinel-1遥感数据的水体提取
本文利用SAR遥感图像进行水体信息的提取,相比光学影像,SAR图像不受天气影响,在应急情况下应用最多,针对水体,在发生洪涝时一般天气都是阴雨天,云较多,光学影像质量较差,基本上都是利…...

C++自定义头文件使用(函数和类)
简单案例需求: 1,计算正方形和三角形的周长——函数 2,模拟不同类型的动物叫声——类 一、创建项目 C空项目 Class_Study 二、创建主函数 在源文件下添加新建项,main.cpp 三、自定义头文件——函数 需求:1&a…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
