MATLAB数组
文章目录
- 数组
- 创建
- 通过冒号创建一维数组
- 通过logspace函数创建一维数组
- 通过linspace函数创建一维数组
- 通过randperm生成随机整数排列
- 运算
- 算术运算
- 关系运算
- 逻辑运算
- 优先顺序
- 矩阵
- 创建
- 矩阵操作
- 下标引用
- 矩阵信息提取
- 删除与扩展
- 合并
- 矩阵元素的运算
- 矩阵运算
数组
在MATLAB中一般使用方括号"[]“、逗号”,“,空格号和分号”;"来创建数组,数组中同一行的元素使用逗号或空格进行分隔,不同行之间用分数进行分隔。
创建
通过冒号创建一维数组
x=A:step:B
A是创建一维数组的第一个变量,step是每次递增或递减的数值,直到最后一个元素和B的差的绝对值小于等于step的绝对值为止。
通过logspace函数创建一维数组
y=logspace(a,b)
该函数创建行向量,第一个元素为 1 0 a 10^a 10a,最后一个元素 1 0 b 10^b 10b,形成总数为50个元素的等比数列。
y=logspace(a,b,n)
该函数创建行向量,第一个元素为 1 0 a 10^a 10a,最后一个元素 1 0 b 10^b 10b,形成总数为n个元素的等比数列。
通过linspace函数创建一维数组
y=linspace(a,b)
该函数创建行向量,第一个元素为 a a a,最后一个元素 b b b,形成总数为100个元素的等差数列。
y=linspace(a,b,n)
该函数创建行向量,第一个元素为 a a a,最后一个元素 b b b,形成总数为n个元素的等差数列。
通过randperm生成随机整数排列
P=randperm(N);%生成一个[1,2,..,N]的一个随机排列
P=randperm(N,K);%生成一个长度为K的向量,其中元素取自1~N间的整数,无重复
perms(a);%返回向量a的全排列
运算
算术运算
- +,-:数组间加法、减法运算直接对对应元素进行操作,要求是数组A、B维数相同
- ./、.*、.\:数组间的乘除运算直接对对应元素进行操作,要求是数组A、B维数相同,其中A./B=B.\A
- .^:实现乘方,数组对数组表示数组各个元素对另一个数组各个元素进行乘方操作,要求维数相同,标量对数组乘方和数组对标量都是各个元素与标量之间的运算
- dot():点积操作,要求维数相同
关系运算
<、<=、>、>=、==、~=
逻辑运算
&、|、~
优先顺序
- 括号
- 转置和乘幂
- 乘除
- 加减
- 冒号
- 关系运算
- 逻辑运算
矩阵
矩阵是数学上的概念,而数组是计算机程序设计领域的概念。
创建
矩阵的创建有两种方法,一种是采用"[]",将矩阵元素置于方括号内,同行元素之间用空格或逗号隔开,行与行之间用分号隔开,另一种就是创建特殊矩阵。
OneMatrix = ones(2);%构建全1矩阵 ones(m,n,...,p)
zerosMatrx = zeros(2);%构建全0矩阵 zeros(m,n,...,p)
Identity = eye(2);%构建单位矩阵 eye(2,3) eye(3,2)
Random = rand(2,3);%构建随机矩阵,0到1之间均匀分布
R=randi(IMAX,N);%返回一个N*N随机矩阵,矩阵中的元素为1~MAX之间的均匀分布随机整数
R=randi(IMAX,M,N);%返回一个N*M随机矩阵,矩阵中的元素为1~MAX之间的均匀分布随机整数
矩阵操作
Randoma = randn(1,4);%构建随机矩阵,均值为0,单位方差的正态分布随机数
Randoma = reshape(Randoma,2,2);%生成2*2的矩阵,元素按现行索引的顺序从Randoma中取
Randoma = fliplr(Rnadoma);%将矩阵的每一行逆序排列
下标引用
矩阵可以通过双下标引用和单下标引用两种方式获得元素,其中单下标引用列优先。
IND = sub2ind(size,i,j);%将双下标索引转换为单下标索引
[I J] = ind3sub(size,ind);%将单下标转换为双下标索引
矩阵信息提取
%获取矩阵结构
A = zeres(4,4);%构造全0矩阵
isempty(A);%判断矩阵A是否为空
isscalar(A);%判断矩阵A是否是标量
isvector(A);%判断矩阵A是否是向量
issparse(A);%判断矩阵A是否为稀疏矩阵%获取矩阵大小
ndims(A);%获取矩阵维数
[m,n]=size(A);%获取矩阵各维长度
length(A);%获取最长维的长度
numel(A);%获取矩阵元素个数
删除与扩展
A=[1 1;2 2];%初始化矩阵
A(3,:)=3;%整行扩展赋值
A(4,1)=4;A(4,2)=5;%单个元素赋值增加新元素
A(2,:)=[];%删除整行
合并
A=[2 0 -1;1 3 2];
B=[1 7 -1;4 2 3;2 0 1];
C=[1 0 1 0;-1 2 0 1];
MAB1=cat(1,A,B);%按行合并=horcat(A,B)=[A,B]
MAB2=cat(2,A,C);%按列合并==vercat(A,C)=[A;C]
Y=blkdiag(A,B,C);%构造对角化矩阵
矩阵元素的运算
基本运算和数组类似
A\B;%表示A的逆矩阵乘以B
A/B;%表示A乘以B的逆矩阵B=sort(A);%表示对A按列进行升序排序
B=sort(A,dim);%若dim为1按列升序,若dim为2,按行升序
B=sort(A,dim,mode);%若mode为'ascend',则升序,若mode为'descend',则降序B=sum(A);%计算各列元素之和,返回行向量
B=sum(A,dim);%若dim为1,则同上;若为2,则计算各行向量之和,返回列向量
B=cumsum(A);%返回一个矩阵,第n行表示每列第1到n个数的和
B=cumsum(A,dim);%若dim为1,则同上;若为2,则返回一个矩阵,第n列表示每行第1到n个数的和%下列是求积运算,形式与求和一样
B=prod(A);
B=prod(A,dim);
B=cumprod(A);
B=cumprod(A,dim);%差分运算:将矩阵元素某行(列)减去上一行(列)的结果保存在该行(列)
A=magic(3);
B=diff(A);%将矩阵元素某行减去上一行的结果保存在该行
C=diff(A,2);%2阶差分,即对一阶差分的矩阵再做一次差分
D=diff(A,1,dim);%dim取1表示按列,取2表示按行
矩阵运算
%范数
a=[1 2 3;4 5 6;7 8 9;];
b=norm(a);%默认二阶范数,可带参数%秩
c=rank(a);%行列式
d=det(a);%迹,表示对角线元素的和
e=trace(a);
相关文章:

MATLAB数组
文章目录 数组创建通过冒号创建一维数组通过logspace函数创建一维数组通过linspace函数创建一维数组 通过randperm生成随机整数排列运算算术运算关系运算逻辑运算优先顺序 矩阵创建矩阵操作下标引用矩阵信息提取删除与扩展合并矩阵元素的运算矩阵运算 数组 在MATLAB中一般使用…...
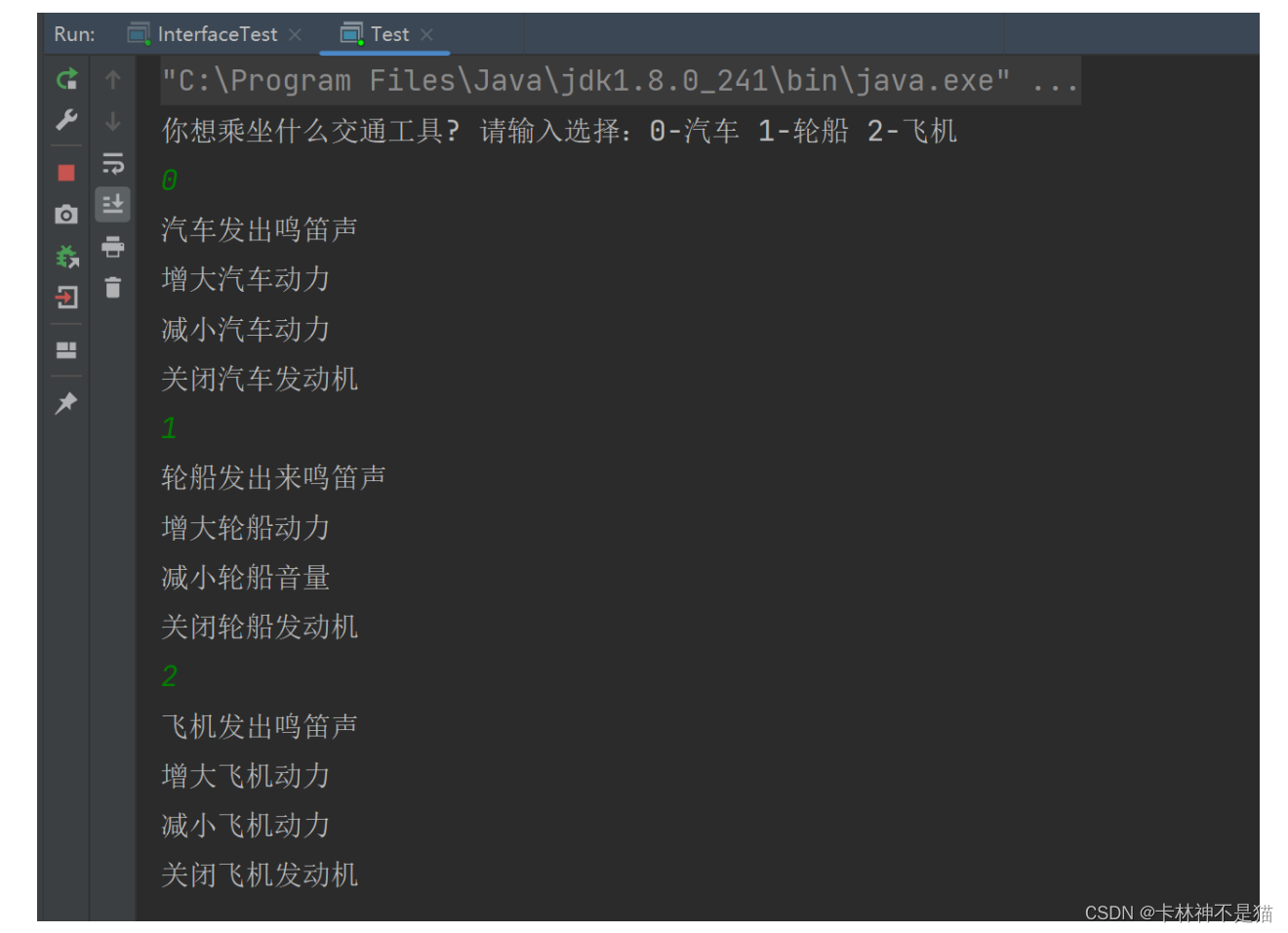
JAVA实验项目(二): 抽象类、接口的定义与使用
实验项目二 抽象类、接口的定义与使用 Tips:"分享是快乐的源泉💧,在我的博客里,不仅有知识的海洋🌊,还有满满的正能量加持💪,快来和我一起分享这份快乐吧😊&…...

JVM内存模型最新面试题(持续更新)
问题:java中创建的对象一般放在哪里?(全流程包含从创建到回收) 回答 大部分对象在堆中,这个基本都知道; 少部分对象是会在栈中的,比如作用域不局限于方法内的方法内部变量,这类对象的特征一般就是生命周期…...

Nginx wss to ws 折腾记
jssip 或 sipml5 <----wss--->nginx<---ws---->fs(5066) fs_cli -x sofia loglevel all 9 日志如下: REGISTER sip:192.168.43.135 SIP/2.0 Via: SIP/2.0/WSS df7jal23ls0d.invalid;branchz9hG4bKurFnCK9qJuXQlSrbszSL1S6wbCokKlLr;rport From: <…...

Java入门基础学习笔记22——程序流程控制
程序流程控制:控制程序的执行顺序。 程序有哪些执行顺序? 顺序、分支和循环。 分支结构: if、switch 循环: for、while、do-while 顺序结构是程序中最简单最基本的流程控制,没有特定的语法结构,按照代码…...

java医院信息系统HIS源码SaaS模式Java版云HIS系统 接口技术RESTful API + WebSocket + WebService
java医院信息系统HIS源码SaaS模式Java版云HIS系统 接口技术RESTful API WebSocket WebService 云HIS是基于云计算的医疗卫生信息系统(Cloud-Based Healthcare Information System),它运用云计算、大数据、物联网等新兴信息技术,…...

2024年成都高新区支持企业申报国家、省级、市级大数据产业发展、新一代信息技术与制造业融合发展、工业互联网推广应用等试点示范项目申报对象条件和奖补
一、申报对象 (一)本政策支持注册地址、税收关系在成都高新区,具有独立法人资格的企业。 (二)管理规范,无不良信用记录,自觉遵守安全生产、环境保护等方面的法律法规,近三年未发生…...

让《行列视》解放数据力量,提升业务洞察
在当今信息化浪潮下,数据已经成为企业发展的核心驱动力之一。如何更好地管理和利用数据,已成为企业发展过程中亟需解决的问题之一。而报表工具作为数据可视化和分析的利器,正逐渐受到企业的重视和青睐。 一、《行列视》作为报表工具的重要性…...

LeetCode 每日一题 ---- 【2244.完成所有任务需要的最少轮数】
LeetCode 每日一题 ---- 【2244.完成所有任务需要的最少轮数】 2244.完成所有任务需要的最少轮数方法:哈希表贪心 2244.完成所有任务需要的最少轮数 方法:哈希表贪心 用哈希表统计每个等级出现的次数 每次处理优先消费 3 个,m % 3 后&#…...

【RAG 去噪】引入 NLI 模型来为 RAG 去噪
论文:Making Retrieval-Augmented Language Models Robust to Irrelevant Context ⭐⭐⭐ ICLR 2024, arXiv:2310.01558 Code: github.com/oriyor/ret-robust 论文速读 这篇论文引入 NLI(Natural Language Inference)模型来判定 retrieved d…...
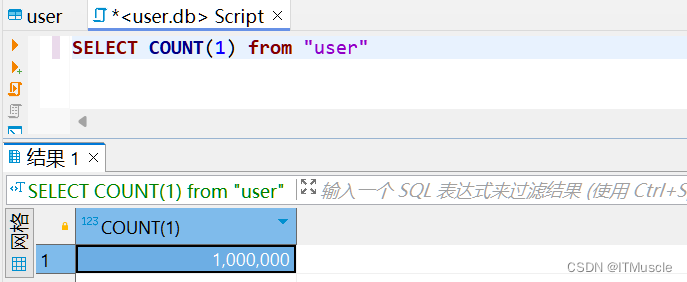
SQLite利用事务实现批量插入(提升效率)
在尝试过SQLite批量插入一百万条记录,执行时长高达20多分钟后,就在想一个问题,这样的性能是不可能被广泛应用的,更不可能出现在真实的生产环境中,那么对此应该如何优化一下呢? 首先分析一下批量插入的逻辑 …...

使用Python处理Excel数据:去除列中的双引号
目录 引言 技术背景 步骤概述 代码示例 案例分析 扩展内容 1. 处理多个列中的双引号 2. 处理大型Excel文件 3. 自定义函数处理数据 4. 错误处理和日志记录 结论 引言 在当今信息爆炸的时代,数据已经成为了各个行业最宝贵的资源之一。而Excel,…...

未来互联网:Web3的技术革新之路
引言 随着技术的不断发展和社会的日益数字化,互联网作为信息交流和社交媒介的重要平台已经成为我们生活中不可或缺的一部分。然而,传统的互联网架构在数据安全、隐私保护和去中心化等方面存在着诸多挑战。为了解决这些问题,Web3技术应运而生…...

【练习】分治--快排思想
🎥 个人主页:Dikz12🔥个人专栏:算法(Java)📕格言:吾愚多不敏,而愿加学欢迎大家👍点赞✍评论⭐收藏 目录 颜色分类 题目描述 题解 代码实现 排序数组 题目描述 题解 代码…...

Unity读书系列《Unity高级编程:主程手记》——C#技术要点
文章目录 前言一、业务逻辑优化技巧二、Unity3d中C#的底层原理三、List底层源码剖析四、Dictionary底层源码剖析五、浮点数的精度问题六、委托、事件、装箱、拆箱七、算法总结 前言 本文旨在总结某一概念的性质,并引出相关的技术要点。如果读者希望深入了解相关技术…...
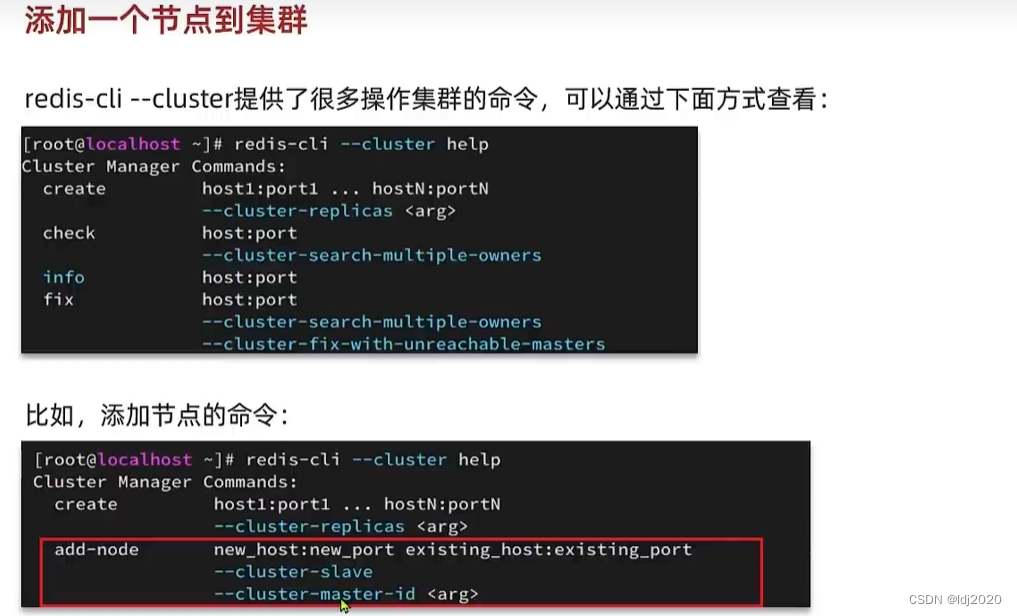
Redis分片集群
哨兵集群虽然解决了高可用和高并发读问题,但是还是有缺陷 1. 因为是主节点是单节点,并发写存在瓶颈 2.数据量大了每个节点存储相同的数据,造成内存紧张,资源浪费 redis.conf文件 port 6379 # 开启集群功能 cluster-enabled yes…...

Math.Round()函数说明
Math.Round()并不是严格意义上的是四舍五入函数。它默认的执行的是“银行家舍入”算法,即四舍六入五取偶。概括为:四舍六入五考虑、五后非零就进一,五后皆零看奇偶,五前为偶应舍去、五前为奇要进一。 当为5时,取离着最…...

001 定期同步mysql数据到es 删除数据库记录同时删除es记录 es全文搜索分词和高亮
文章目录 ProductController.javaProduct.javaElasticsearchSyncListener.javaProductElasticSearchMapper.javaProductMapper.javaProductDeletedEvent.javaProductServiceImpl.javaSyncProductService.javaIProductService.javaElasticSearchSpringDemoApplication.javaServl…...

Vue 快速入门:Vue初级
语法规则 前端渲染 渲染有几种方式:原生js、js模板、Vue模板语法 原生js 使用字符串拼接 js模板语法 Vue.js 模板语法概述 Vue.js 是一个用于构建用户界面的渐进式框架,其模板语法非常灵活和直观。Vue 的模板语法基于 HTML,可以通过指令…...
什么是IP跳变?
IP 跳跃(也称为 IP 跳动)的概念已引起使用代理访问网站的用户的极大关注。但 IP 跳跃到底是什么?为什么它对于各种在线活动至关重要? 在本文中,我们将深入探讨 IP 跳跃的世界,探索其实际应用、用例、潜在问…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...
