洛谷 P3203:弹飞绵羊 ← 分块算法(单点更新、单点查询)
【题目来源】
https://www.acwing.com/problem/content/2168/
https://www.luogu.com.cn/problem/P3203
【题目描述】
某天,Lostmonkey 发明了一种超级弹力装置,为了在他的绵羊朋友面前显摆,他邀请小绵羊一起玩个游戏。
游戏一开始,Lostmonkey 在地上沿着一条直线摆上 n 个装置,每个装置设定初始弹力系数 ki,当绵羊达到第 i 个装置时,它会往后弹 ki 步,达到第 i+ki 个装置,若不存在第 i+ki 个装置,则绵羊被弹飞。
绵羊想知道当它从第 i 个装置起步时,被弹几次后会被弹飞。为了使得游戏更有趣,Lostmonkey 可以修改某个弹力装置的弹力系数,任何时候弹力系数均为正整数。
【输入格式】
第一行包含一个整数 n,表示地上有 n 个装置,装置的编号从 0∼n−1。
接下来一行有 n 个正整数,依次为那 n 个装置的初始弹力系数。
第三行有一个正整数 m,表示操作次数。接下来 m 行每行至少有两个数 i,j。
(1)若 i=1,你要输出从编号为 j 的装置出发被弹几次后被弹飞
(2)若 i=2,则还会再输入一个正整数 k,表示编号为 j 的弹力装置的系数被修改成 k。
【输出格式】
对于每个 i=1 的操作,输出一行一个整数表示答案。
【输入样例】
4
1 2 1 1
3
1 1
2 1 1
1 1
【输出样例】
2
3
【算法分析】
● 本题其实就是动态树 LCT 的模板题,这里用来练习分块。
● 分块算法(区间更新、区间查询)代码实例详见:https://blog.csdn.net/hnjzsyjyj/article/details/138863063
本例介绍各数组下标从 0 开始的分块算法(单点更新、单点查询)代码。
● 分块是用线段树的分区思想改良的暴力法。代码比线段树简单。效率比普通暴力法高。分块适合求解 m=n=10^5 规模的问题。或 m*sqrt(n)≈10^7 的问题。其中,n 为元素个数,m 为操作次数。
● 分块操作的基本要素
(1)块的大小用 block 表示。通常,令 block=sqrt(n)。其中,n 为元素个数。
(2)块的数量用 cnt 表示。计算块的数量的代码如下:
int block=sqrt(n);
int cnt=n/block;
if(n % block) cnt++;(3)块的左边界 le[] 及右边界 ri[]。
若用 le[i] 和 ri[i] 分别表示块 i 的第一个和最后一个元素的位置。
若下标从 1 开始,则有:
le[1]=1, ri[1]=block;
le[2]=block+1, ri[2]=2*block;
……
le[i]=(i-1)*block+1, ri[i]=i*block;
……若下标从 0 开始,则有:
le[0]=0, ri[0]=block-1;
le[1]=block, ri[1]=2*block-1;
……
le[i]=i*block, ri[i]=(i+1)*block-1;
……(4)定义 pos[i] 为第 i 个元素所在的块。
若下标从 1 开始,则有 pos[i]=(i-1)/block+1。其中,block=sqrt(n)。
若下标从 0 开始,则有 pos[i]=i/block。其中,block=sqrt(n)。
● 数组 step[x],表示从 x 跳出当前块所用步数;数组 to[x],表示从 x 跳出当前块到达的位置。
【算法代码】
#include <bits/stdc++.h>
using namespace std;const int maxn=1e6+5;
int a[maxn],le[maxn],ri[maxn];
int pos[maxn];
int to[maxn],step[maxn];
int n,m;void build(int n) {int block=sqrt(n);int cnt=n/block;if(n%block) cnt++;for(int i=0; i<cnt; i++) {le[i]=i*block;ri[i]=(i+1)*block-1;}ri[cnt-1]=n-1;for(int i=0; i<n; i++) pos[i]=i/block;
}void update(int L, int R) {for(int i=R; i>=L; i--) {if(i+a[i]>ri[pos[i]]) {to[i]=i+a[i];step[i]=1;} else {to[i]=to[i+a[i]];step[i]=step[i+a[i]]+1;}}
}int query(int x) {int ans=0;while(x<n) {ans+=step[x];x=to[x];}return ans;
}int main() {cin>>n;for(int i=0; i<n; i++) cin>>a[i];build(n), update(0,n-1);cin>>m;while(m--) {int op,x,y;cin>>op>>x;if(op==1) cout<<query(x)<<endl;else {cin>>y;a[x]=y;update(le[pos[x]],ri[pos[x]]);}}return 0;
}/*
in:
4
1 2 1 1
3
1 1
2 1 1
1 1out:
2
3
*/
【参考文献】
https://blog.csdn.net/hnjzsyjyj/article/details/138863063
https://www.acwing.com/solution/content/92055/
https://www.acwing.com/solution/content/170541/
https://www.luogu.com.cn/problem/solution/P3203
https://www.cnblogs.com/xuyixuan/p/9462001.html
相关文章:
)
洛谷 P3203:弹飞绵羊 ← 分块算法(单点更新、单点查询)
【题目来源】https://www.acwing.com/problem/content/2168/https://www.luogu.com.cn/problem/P3203【题目描述】 某天,Lostmonkey 发明了一种超级弹力装置,为了在他的绵羊朋友面前显摆,他邀请小绵羊一起玩个游戏。 游戏一开始,L…...
程序验证之Dafny--证明霍尔逻辑的半自动化利器
一、What is Dafny?【来自官网介绍 Dafny 】 1)介绍 Dafny 是一种支持验证的编程语言,配备了一个静态程序验证器。 通过将复杂的自动推理与熟悉的编程习语和工具相结合,使开发者能够编写可证明正确的代码(相对于 {P}S{Q} 这种…...

Flutter 中的 SafeArea 小部件:全面指南
Flutter 中的 SafeArea 小部件:全面指南 在移动应用开发中,处理设备屏幕的边缘是一个常见的挑战,尤其是考虑到现代设备通常具有不同的屏幕形状,如刘海屏、曲面屏等。为了确保应用内容不会覆盖这些屏幕区域,Flutter 提…...
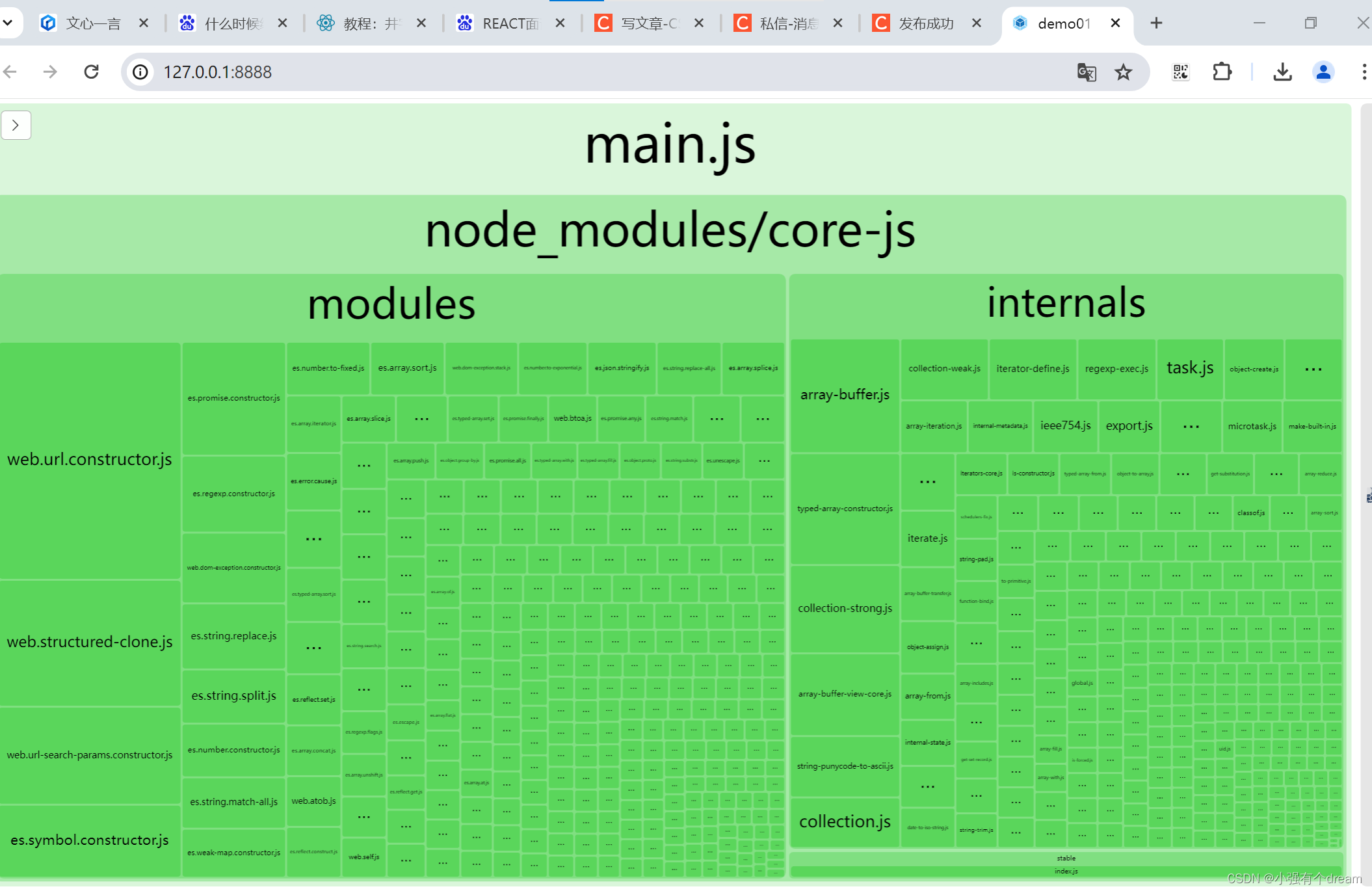
webpack生成模块关系依赖图示例:查看构建产物的组成部分 依赖关系图
npm i -D webpack-bundle-analyzer core-js babel-loaderwebpack.config.js const BundleAnalyzerPlugin require(webpack-bundle-analyzer).BundleAnalyzerPlugin; module.exports {entry: ./src/index.js,output: {filename: main.js,},// mode: production, // 或者 produ…...

Spacy的安装与使用教程
官网安装指导教程 https://spacy.io/usage 安装指令 需要根据自己系统的cuda版本选择 nvcc -V pip install -U pip setuptools wheel pip install -U spacy[cuda12x] python -m spacy download zh_core_web_sm python -m spacy download en_core_web_sm...

Pathlib,一个不怕迷路的 Python 向导
大家好!我是爱摸鱼的小鸿,关注我,收看每期的编程干货。 一个简单的库,也许能够开启我们的智慧之门, 一个普通的方法,也许能在危急时刻挽救我们于水深火热, 一个新颖的思维方式,也许能…...

详解绝对路径和相对路径的区别
绝对路径和相对路径是用于描述文件或目录在文件系统中位置的两种不同方式。 绝对路径(Absolute Path)是从文件系统的根目录开始的完整路径,可以唯一地确定一个文件或目录的位置。在不同的操作系统中,根目录的表示方式可能略有不同…...
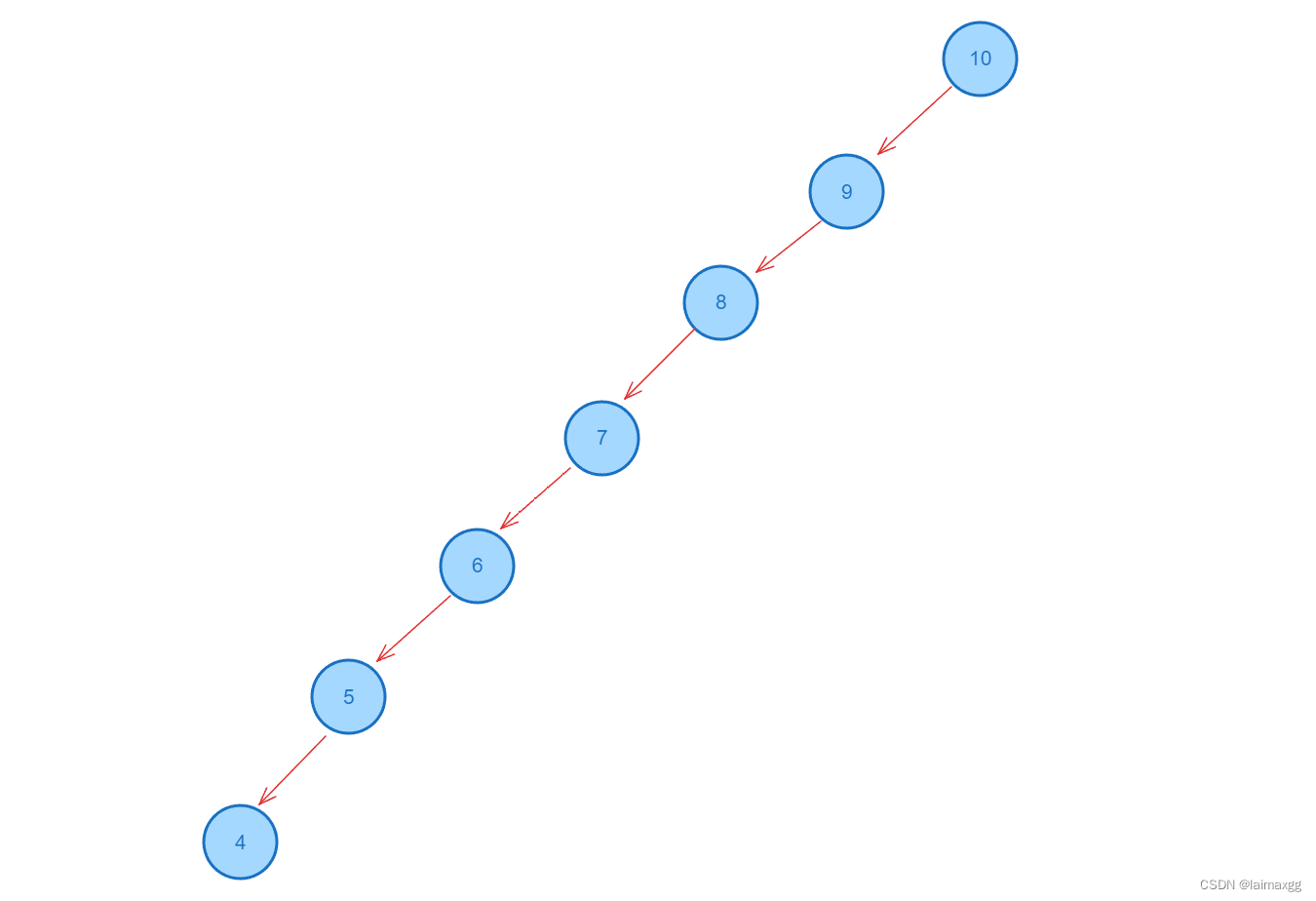
C++二叉搜索树搜索二叉树二叉排序树
C二叉搜索树 1. 二叉搜索树的概念 二叉搜索树(BST,Binary Search Tree),也称为二叉排序树或二叉查找树。它与一般二叉树的区别在于:每个结点必须满足“左孩子大于自己,右孩子小于自己”的规则。在这种规则的约束下,二…...

Java 自然排序和比较器排序区别?Comparable接口和Comparator比较器区别?
注:如果你对排序不理解,请您耐心看完,你一定会明白的。文章通俗易懂。建议用idea运行一下案例。 1)自然排序和比较器排序的区别? 自然排序是对象本身定义的排序规则,由对象实现 Comparable 接口ÿ…...

【CV】opencv调用DIS/LK等计算光流,前一帧和当前帧写反了有什么影响?
当在计算光流时,将前一帧和当前帧输入反了,会导致一系列问题。 在计算光流时,通常是将前一帧作为模板,根据当前帧计算光流。因为光流是描述相邻帧之间像素移动的一种方法,它通过比较两帧之间的像素强度或特征点的移动…...

C语言学习细节|C语言面向对象编程!函数指针如何正确使用
文章目录 1.函数指针定义2.格式3.应用回调函数动态函数调用函数的间接调用 4.结构体与函数指针结合 1.函数指针定义 函数指针就是一个指向函数的指针变量,与指向数据的指针不同,函数指针保存的是函数的地址,这使得程序可以动态地调用不同的函…...

C语言简要(一)
总得让她开心吧 helloworld #include <stdio.h>int main() {printf("hello world!\n");return 0; } 程序框架 #include <stdio.h> int main {return 0; }输出 printf("hello world!\n"); "里面的内容叫做“字符串”,prin…...

那些年我与c++的叫板(一)--string类自实现
引子:我们学习了c中的string类,那我们能不能像以前数据结构一样自己实现string类呢?以下是cplusplus下的string类,我们参考参考! 废话不多说,直接代码实现:(注意函数之间的复用&…...
)
二刷算法训练营Day08 | 字符串(1/2)
今日任务: 344.反转字符串 541. 反转字符串II卡码网:54.替换数字 151.翻转字符串里的单词卡码网:55.右旋转字符串 详细布置: 1. 344. 反转字符串 编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 …...

使用高防IP是应对网络安全的重要措施
使用高防IP(High Defense IP)在现代网络环境中显得尤为重要,这主要源于以下几个方面的原因: 一、网络安全形势严峻 随着互联网的快速发展,网络安全问题日益突出。各种网络攻击手段层出不穷,如分布式拒绝服…...

代码随想录-算法训练营day40【动态规划03:整数拆分、不同的二叉搜索树】
代码随想录-035期-算法训练营【博客笔记汇总表】-CSDN博客 第九章 动态规划part03● 343.整数拆分 ● 096.不同的二叉搜索树 详细布置 今天两题都挺有难度,建议大家思考一下没思路,直接看题解,第一次做,硬想很难想出来。343. 整数…...
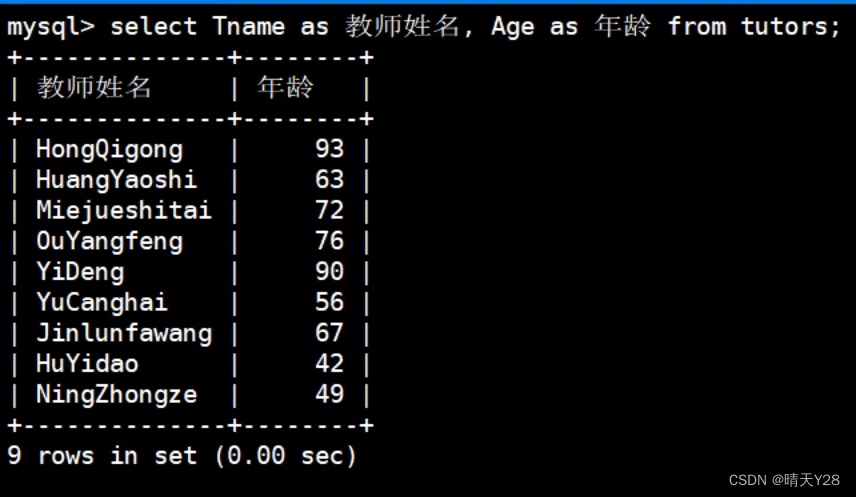
MySQL数据库中基本数据管理操作
使用SQL语句实现基本数据管理操作——即DML语句 1.添加数据 insert into 表名(字段名称,字段名称,字段名称)values(数据,数据,数据) 在MySQL数据库中,除了数字&#x…...

记录一下Hql遇到的零碎问题
建表相关 -- 地区维度表 drop table dim_province_full; create table dim_province_full( id string comment 编号, name string comment 省份名称, region_id string comment 大区id, area_code string comment 行政区位码, iso_code string comment 国际编码, iso_3166_2 s…...

Flutter 中的 TextField 小部件:全面指南
Flutter 中的 TextField 小部件:全面指南 在 Flutter 中,TextField 是一个允许用户输入文本的小部件。它非常灵活,支持多种文本输入场景,如单行文本、多行文本、密码输入、数值输入等。TextField 还提供了丰富的定制选项…...
GPT-4o:全面深入了解 OpenAI 的 GPT-4o
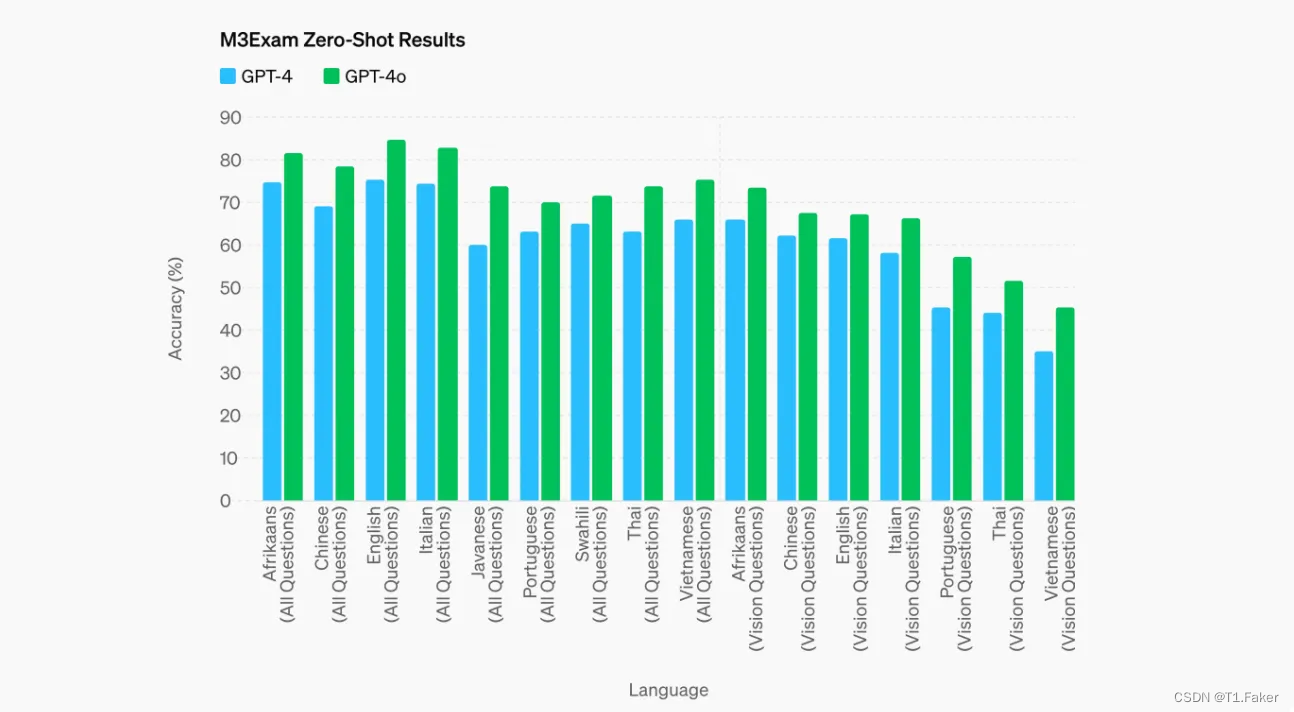
GPT-4o:全面深入了解 OpenAI 的 GPT-4o 关于 GPT-4o 的所有信息ChatGPT 增强的用户体验改进的多语言和音频功能GPT-4o 优于 Whisper-v3M3Exam 基准测试中的表现 GPT-4o 的起源追踪语言模型的演变GPT 谱系:人工智能语言的开拓者多模式飞跃:超越…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...
