一篇讲透排序算法之插入排序and选择排序
1.插入排序
1.1算法思想
先将数组的第一个元素当作有序,让其后一个元素与其比较,如果比第一个元素小则互换位置,之后再将前两个元素当作有序的,让第三个元素与前两个元素倒着依次进行比较,如果第三个元素比第二个元素小的话,则交换位置,之后再比较第二个元素和第一个元素。
之后我们重复以上操作即可完成插入排序。
为了帮助大家理解,现在我们一步步完成这些操作。
1.2实现逻辑以及具体实现
首先,如果第二个元素小于第一个元素,则交换位置。
if (a[1] < a[0]){int tmp = a[1];a[1] = a[0];a[0] = tmp;}之后,我们就可以让第三个元素依次与前两个元素进行比较了。
在这里,我们要记录一下第二个元素的位置,否则我们不知道如何比较。
因此我们在这里定义一个end来记录第二个元素的位置。
int end = 1;
while (end)
{//如果第三个元素和第二个元素发生了交换//则比较第一个元素和新的第二个元素if (a[end + 1] < a[end]){int tmp = a[end + 1];a[end + 1] = a[end];a[end] = tmp;}//由于前end个元素已经有序,所以有一次没有进if就可以跳出循环了else{break;}end--;
}现在我们就完成了单趟的循环,但我们需要比较多趟,而每趟的比较中不一样的变量就是end,每趟的比较end都会+1,因此我们在外层再写一个循环即可。
for (int i = 0; i < n-1; i++){int end = i;while (end >= 0){if (tmp < a[end]){int tmp = a[end + 1];a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;}到这里我们已经完成了一次插入排序,最后我们只需要将这些内容放在函数定义当中即可彻底完成!
void InsertSort(int* a, int n)
{for (int i = 0; i < n-1; i++){int end = i;while (end >= 0){if (tmp < a[end]){int tmp = a[end + 1];a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;}
}2.选择排序
2.1算法思想
先遍历一遍数组,找出最小的元素,然后与第一个元素交换位置。
之后从数组的第二个数开始,再遍历一遍数组,找出此次遍历中最小的数,与第二个数交换位置。
之后重复以上的操作即可完成任务。
使用上述的原理遍历数组,每次遍历都可以选出一个最小的数,放到对应的位置上面去。
2.2实现逻辑以及具体实现
现在我们来逐步实现这个排序算法
首先,我们应遍历数组,找出最小的元素。
int min=a[0];
for (int i = 0; i < n; i++)
{if (a[i] < min){int tmp = min;min = a[i];a[i] = tmp;}
}我们这样写出现了一个问题,我们交换了min和a[i]的数值,但是a[0]处的数值并没有随着min的改变而改变,对此,我们应该怎么做呢?
这里我们可以将两数交换封装为一个函数,之后我们不再让min记录数值,而是记录下标即可。
//假设最小的是下标为0处的元素
int min = 0;
for (int i = 0; i < n; i++)
{if (a[i] < a[min]){//交换下标,每次交换后,min中记录的则是较小数的下标//之后进入下一次循环,继续比较min = i;}
}
//比较完毕之后,交换数值即可
swap(&arr[min], &arr[0]);//这个函数自己写,我没贴上来。现在我们已经找到了最小的数,而且已经将其放到了第一个位置上去。
现在我们只需要在外面再套一层循环,每次不断更新下标,即可完成选择排序。
for (int i = 0; i <n-1; i++)//一共需要比较n-1趟
{//此时i下标元素最小int min = i;for (int j = i+1; j < n; j++)//前i个有序,因此j=i+1,比较n个元素,因此j<n{//假设最小的是下标为j处的元素if (a[j] < a[min]){//交换下标,每次交换后,min中记录的则是较小数的下标//之后进入下一次循环,继续比较min = j;}}//比较完毕之后,交换数值即可swap(&arr[min], &arr[0]);
}我们将其封装在函数体内,即可完成一次排序。
void SelectSort(int* arr, int len)
{for (int i = 0; i < len - 1; i++){int min = i;for (int j = i + 1; j < len; j++){if (arr[j] < arr[min]){mini = j;}}swap(&arr[min], &arr[i]);}
}
2.3选择排序的优化
我们的选择排序还可以进行一下优化,我们可以一次循环同时找最小和最大的数据,只需要在每次比较时定义一个min,一个max,即可在一次循环中找到最小和最大的数据。
这里我们还是先完成第一趟排序,代码如下
int max = 0;
int min = 0;
for (int j =1; j < n; j++)//前i个有序,因此j=i+1,比较n个元素,因此j《n
{//假设最小的是下标为j处的元素if (a[j] < a[min]){//交换下标,每次交换后,min中记录的则是较小数的下标min = j;}if (a[j] > a[max]){//交换下标,每次交换后,min中记录的则是较大数的下标max = j;}
}
swap(&arr[min], &arr[0]);
swap(&arr[max], &arr[n-1]);通过上面这段代码,我相信大家可以了解优化的原理了。
现在我们就可以着手于完成优化后的选择排序了。
由于我们在一个循环体内同时寻找最小值和最大值,并交换位置。
因此我们需要两个变量记录每次循环中最左边的值和最右边的值的下标,我们将其定义为begin和end。
当begin和end相遇时,我们的循环就结束了。这时我们的数组就有序了。
当begin>=end时,她们就有序了。因此我们的循环条件可以写为begin<end。
void SelectSort(int* arr, int len)
{int begin = 0;int end = len - 1;while (begin < end){//假设mini和maxi都是beginint mini = begin;int maxi = begin;for (int i = begin + 1; i <= end; i++){//找大if (arr[mini] > arr[i]){mini = i;}//找小if (arr[maxi] < arr[i]){maxi = i;}}swap(&arr[mini], &arr[begin]);swap(&arr[maxi], &arr[end]);begin++;end--;}}
}到了这里,我们的选择排序已经基本完成了,
但是请大家思考一个问题:
如果我们的begin和maxi重合的话,上面这段代码的执行逻辑是什么样的呢?
如果begin和maxi重合,根据我们的代码逻辑,我们首先会交换mini和begin位置处的值。
此时我们的begin下标处的值已经更新成了mini处的值,而由于我们的maxi和begin是相同的,因此此时我们maxi下标处的值其实是mini处的值。
文字表述可能比较抽象,我们现在将文字具象化为代码。
swap(&arr[mini], &arr[begin]);swap(&arr[begin], &arr[end]);
那么应该怎么解决这个问题呢?很简单,因为我们的下标重合了,因此我们在进行完第一个交换之后更新一下maxi的值即可。
void SelectSort(int* arr, int len)
{int begin = 0;int end = len - 1;while (begin < end){//假设mini和maxi都是beginint mini = begin;int maxi = begin;for (int i = begin + 1; i <= end; i++){//找大if (arr[mini] > arr[i]){mini = i;}//找小if (arr[maxi] < arr[i]){maxi = i;}}swap(&arr[mini], &arr[begin]);//begin处的值和mini处的值交换了位置//因此现在mini处保存的值为最大值//我们将maxi更新为mini即可。if (begin == maxi){maxi = mini;}swap(&arr[maxi], &arr[end]);begin++;end--;}}
}相关文章:

一篇讲透排序算法之插入排序and选择排序
1.插入排序 1.1算法思想 先将数组的第一个元素当作有序,让其后一个元素与其比较,如果比第一个元素小则互换位置,之后再将前两个元素当作有序的,让第三个元素与前两个元素倒着依次进行比较,如果第三个元素比第二个元素…...

CompletableFuture的主要用途是什么?
CompletableFuture 的主要用途是为复杂的异步编程模型提供一种更简单,更具可读性的方式。它主要用于以下几个方面: 非阻塞计算:CompletableFuture 为处理高延迟的计算任务提供了非阻塞的解决方案。你可以启动一个计算任务,而不需要…...

QtCreator,动态曲线实例
样式图: .ui 在sloem1.ui文件中,拖入一个label控件, 头文件.h #include "QtGui/QPainter.h" #include "QtCore/QTimer.h"protected:bool eventFilter(QObject *obj,QEvent *event);void labelPaint();public slots: /…...
)
Model-Based Pose Estimation for Rigid Objects(基于SIFT)
6D目标检测工程落地需求的小算力算法,本文具有借鉴意义,但对于特征点少的目标不太好用。 摘要 在多个实际应用中,经常会遇到确定图像中出现的物体姿态的问题。处理这一挑战的最有效策略是按照基于模型的范式进行,这涉及构建物体…...
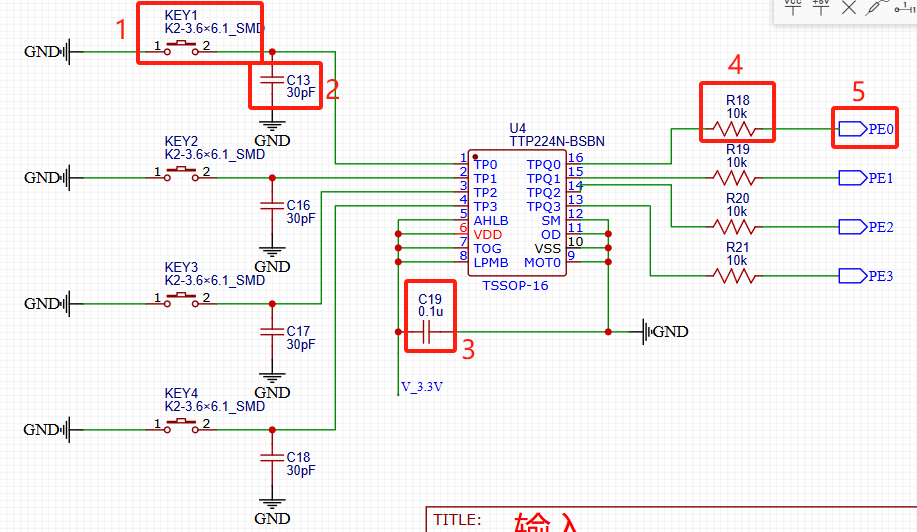
STM32自己从零开始实操02:输入部分原理图
一、触摸按键 1.1指路 项目需求: 4个触摸按键,主控芯片 TTP224N-BSBN(嘉立创,封装 TSSOP-16),接入到 STM32 的 PE0,PE1,PE2,PE3。 1.2走路 1.2.1数据手册重要信息提…...

JavaScript异步编程——03-Ajax传输json和XML的技术文档
JavaScript异步编程——03-Ajax传输json和XML的技术文档 目录 JavaScript异步编程——03-Ajax传输json和XML的技术文档 一、引言 二、Ajax简介 三、Ajax传输JSON数据 四、Ajax传输XML数据 五、总结 一、引言 在现代Web开发中,Ajax技术已经成为实现前后端数据交…...

移动端常用meta
在移动端开发中,<meta> 标签用于提供关于HTML文档的元数据,这些元数据不会显示在页面上,但可以被浏览器解析,用于控制页面的行为和外观。以下是一些在移动端开发中常用的 标签: 1. 视口设置 这是移动端开发中最…...
C++_C++11的学习
1. 统一的列表初始化 1.1{}初始化 在C98 中,标准就已经允许使用花括号 {} 对数组或者结构体元素进行统一的列表初始值设定。而到了C11,标准扩大了用大括号括起的列表 ( 初始化列表 )的使用范围,使其能适用于所有的内…...
RAC11G参数修改错误导致启库失败处理
问题描述 部署完一套3节点的11g RAC后,进行了内存的参数优化,优化时忘记了先备份参数文件,忘记了计算内存参数眼盲的复制粘贴执行内存优化sql导致优化后重启实例启动失败。艾,由于粗心自己给自己挖了个坑。 切记更改参数步骤&am…...

UE4打包Win64项目命令行
仅用于个人记录,写的粗糙,勿喷 BuildProject.bat 具体命名参数请参照UE引擎RunUAT源码(Programs\AutomationTool下Program.cs) 参数1:引擎安装路径 参数2:uproject路径 参数3:输出路径 参数…...

c语言bug汇总中篇5
40. 不关注代码风格一致性 代码风格一致性有助于提高代码的可读性和可维护性。如果团队成员使用不同的代码风格,会导致代码看起来杂乱无章,增加阅读和理解的成本。 为了保持代码风格的一致性,程序员应该: - 遵循团队或项目约定的…...

【linux】进程(一)
1. 冯诺依曼体系结构 计算机基本都遵循着冯诺依曼体系 我们使用的计算器是由一个个硬件构成的: 中央控制器(CPU) : 运算器 控制器 等输入设备 : 键盘,鼠标,网卡 等输出设备 : 显示器,网卡 等…...
手把手教你用Python轻松玩转SQL注入
一、浅谈SQL注入 SQL注入其实就是把SQL命令插入到WEB表单中提交或者输入一些页面请求的查询字符串,比如我们输网址,就是相当于这种操作,只不过我们不是在测试SQL注入漏洞,而仅仅只是为了输入后看到相应网页上的内容而已。一般方法…...

redis的几种部署模式及注意事项
Redis 可以以多种部署模式来满足不同的需求,其中一些常见的部署模式包括:单节点部署、主从复制部署、哨兵模式部署和集群部署。这些部署模式各有特点,适用于不同的场景和需求: 概念 单节点部署: 特点:单…...

使用Python生成一束玫瑰花
520到了,没时间买花?我们来生成一个电子的。 Python不仅是一种强大的编程语言,用于开发应用程序和分析数据,它也可以用来创造美丽的艺术作品。在这篇博客中,我们将探索如何使用Python生成一束玫瑰花的图像。 准备工作…...

紫光同创PGL22G开发板|盘古22K开发板,国产FPGA开发板,接口丰富
盘古22K开发板是基于紫光同创Logos系列PGL22G芯片设计的一款FPGA开发板,全面实现国产化方案,板载资源丰富,高容量、高带宽,外围接口丰富,不仅适用于高校教学,还可以用于实验项目、项目开发,一板…...

大模型的实践应用24-LLaMA-Factory微调通义千问qwen1.5-1.8B模型的实例
大家好,我是微学AI,今天给大家介绍一下大模型的实践应用24-LLaMA-Factory微调通义千问qwen1.5-1.8B模型的实例, LLaMA-Factory是一个专门用于大语言模型微调的框架,它支持多种微调方法,如LoRA、QLoRA等,并提供了丰富的数据集和预训练模型,便于用户进行模型微调。通义千问…...
)
力扣爆刷第142天之二叉树五连刷(构造树、搜索树)
力扣爆刷第142天之二叉树五连刷(构造树、搜索树) 文章目录 力扣爆刷第142天之二叉树五连刷(构造树、搜索树)一、106. 从中序与后序遍历序列构造二叉树二、654. 最大二叉树三、617. 合并二叉树四、700. 二叉搜索树中的搜索五、98. …...
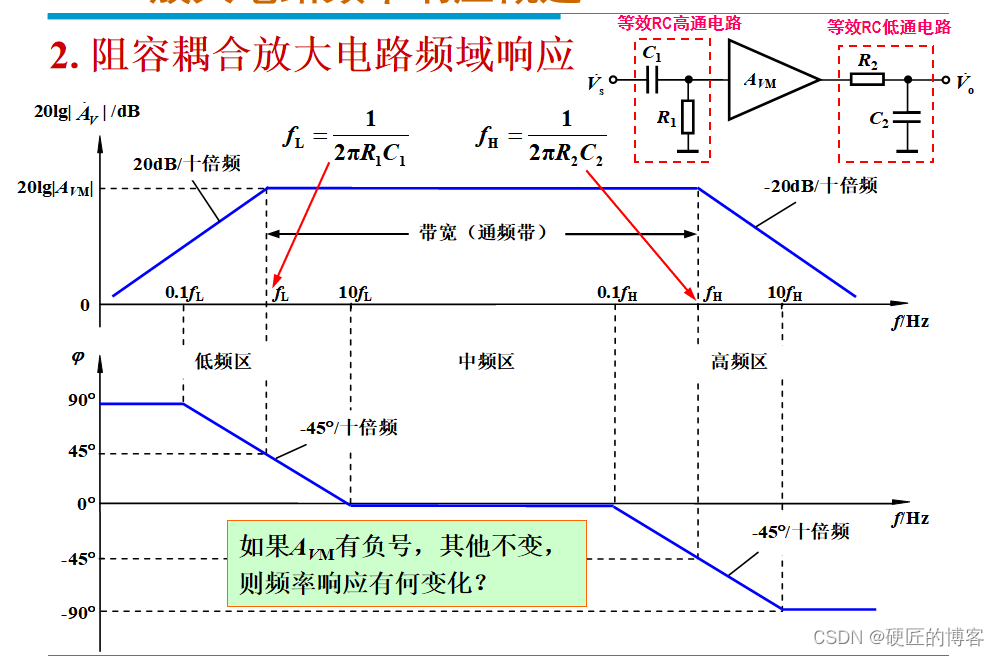
0407放大电路的频率响应
放大电路的频率响应 单时间常数RC电路的频率响应中频响应高频响应低频响应全频域响应 放大电路频率响应概述1. 直接耦合放大电路频域响应阻容耦合放大电路频域响应 4.7.1 单时间常数RC电路的频率响应 4.7.2 放大电路频率响应概述 4.7.3 单级共射极放大电路的频率响应 4.7.4 单级…...
)
数据分析必备:一步步教你如何用Pandas做数据分析(6)
1、Pandas 函数应用 Pandas 重建索引操作实例 要将您自己或其他库的函数应用于Pandas对象,您应该了解三个重要的方法。方法如下所述。要使用的适当方法取决于您的函数是希望对整个数据帧进行操作,还是行操作还是按列操作,还是按元素操作。 表…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

WEB3全栈开发——面试专业技能点P4数据库
一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库,基于 mysql 库改进而来,具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点: 支持 Promise / async-await…...

Python环境安装与虚拟环境配置详解
本文档旨在为Python开发者提供一站式的环境安装与虚拟环境配置指南,适用于Windows、macOS和Linux系统。无论你是初学者还是有经验的开发者,都能在此找到适合自己的环境搭建方法和常见问题的解决方案。 快速开始 一分钟快速安装与虚拟环境配置 # macOS/…...
