蓝桥杯-合并数列
小明发现有很多方案可以把一个很大的正整数拆成若干正整数的和。他采取了其中两种方案,分别将它们列为两个数组 {a1, a2, …, an} 和 {b1, b2, …, bm}。两个数组的和相同。
定义一次合并操作可以将某数组内相邻的两个数合并为一个新数,新数的值是原来两个数的和。小明想通过若干次合并操作将两个数组变成一模一样,即 n=m 且对于任意下标 i 满足 ai=bi。请计算至少需要多少次合并操作可以完成小明的目标。
输入格式
输入共 3 行。
第一行为两个正整数 n, m。
第二行为 n 个由空格隔开的整数 a1, a2, …, an。
第三行为 m 个由空格隔开的整数 b1, b2, …, bm。
输出格式
输出共 1 行,一个整数。
样例输入
4 3
1 2 3 4
1 5 4
样例输出
1
样例说明
只需要将 a2 和 a3 合并,数组 a 变为 {1, 5, 4},即和 b 相同。
评测用例规模与约定
对于 20% 的数据,保证 n, m ≤ 10^3。
对于 100% 的数据,保证 n, m ≤ 10^5,0 < ai, bi ≤ 10^5。
题解:
这题有两种写法, 第一种:模拟队列, 第二种:前缀和+二分
题解一:
模拟队列法
对于两个序列 a 和 b 的开头包含三种情况:
- a[0]等于b[0], 此时把两个开头都删除掉
- b[0] < a[0], 此时把b[0]和b[1]相加, 然后删除b[0]和b[1], 把b[0]和b[1]相加的结果放到b的开头, 相当于是合并b的前两个数, cnt ++ (cnt是总操作数)
- a[0] < b[0], 此时把a[0]和a[1]相加, 然后删除a[0]和a[1], 把a[0]和a[1]相加的结果放到a的开头, 相当于是合并a的前两个数, cnt ++
ac代码👇
#include <bits/stdc++.h>
using namespace std;
#define int long long // 序列中的数最大是1e5, 如果两个都是1e5, 那么这两个数相加会爆int
const int N = 1e5 + 10;
int a[N], b[N];signed main()
{int n, m; cin >> n >> m;for (int i = 0; i < n; i ++) cin >> a[i];for (int j = 0; j < m; j ++) cin >> b[j];int i = 0, j = 0, cnt = 0;while (i < n && j < m) // 也可以用dequeue, 但运行效率会低一些{if (a[i] == b[j]) i ++, j ++; else if (a[i] < b[j]) a[i + 1] = a[i] + a[i + 1], i ++, cnt ++;else if (b[j] < a[i]) b[j + 1] = b[j] + b[j + 1], j ++, cnt ++;}cout << cnt << endl;return 0;
}
题解二:
前缀和+二分法
- 先对两个序列都求一次前缀和
- 当前缀和相同的时候跳过, 不同的时候分为两种情况:
- a<b的时候, 用二分查找一下"第一个等于b的值得下标", 然后加上操作次数; b<a的时候, 用二分查找一下"第一个等于a的值得下标", 然后加上操作次数
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e5 + 10; // 会爆int
int a[N], b[N];signed main()
{int n, m; cin >> n >> m;for (int i = 1; i <= n; i ++) {cin >> a[i];a[i] += a[i - 1]; // 求前缀和}for (int j = 1; j <= m; j ++) {cin >> b[j];b[j] += b[j - 1]; // 求前缀和}int i = 1, j = 1, cnt = 0;while (i <= n && j <= m) {if (a[i] == b[j]) i ++, j ++;else if (a[i] < b[j]){int l = i, r = n;while (l < r){int mid = l + r >> 1;if (a[mid] >= b[j]) r = mid; // 找到的是第一个满足 条件的下标 else l = mid + 1;}cnt += l - i;i = l;}else if (b[j] < a[i]){int l = j, r = m;while (l < r){int mid = l + r >> 1;if (b[mid] >= a[i]) r = mid; // 找到的是第一个满足 条件的下标else l = mid + 1;}cnt += l - j;j = l;}}cout << cnt << endl;return 0;
}
觉得写的不错的话, 点个赞吧~
相关文章:

蓝桥杯-合并数列
小明发现有很多方案可以把一个很大的正整数拆成若干正整数的和。他采取了其中两种方案,分别将它们列为两个数组 {a1, a2, …, an} 和 {b1, b2, …, bm}。两个数组的和相同。 定义一次合并操作可以将某数组内相邻的两个数合并为一个新数,新数的值是原来两…...

《web应用技术》第9次课后作业
一、将前面的代码继续完善功能 1、采用XML映射文件的形式来映射sql语句; 2、采用动态sql语句的方式,实现条件查询的分页。 二、学习git的使用。 1、每个小组将自己的项目上传到gitee,学会协作开发; 2、学会从gitee上拉取项目…...
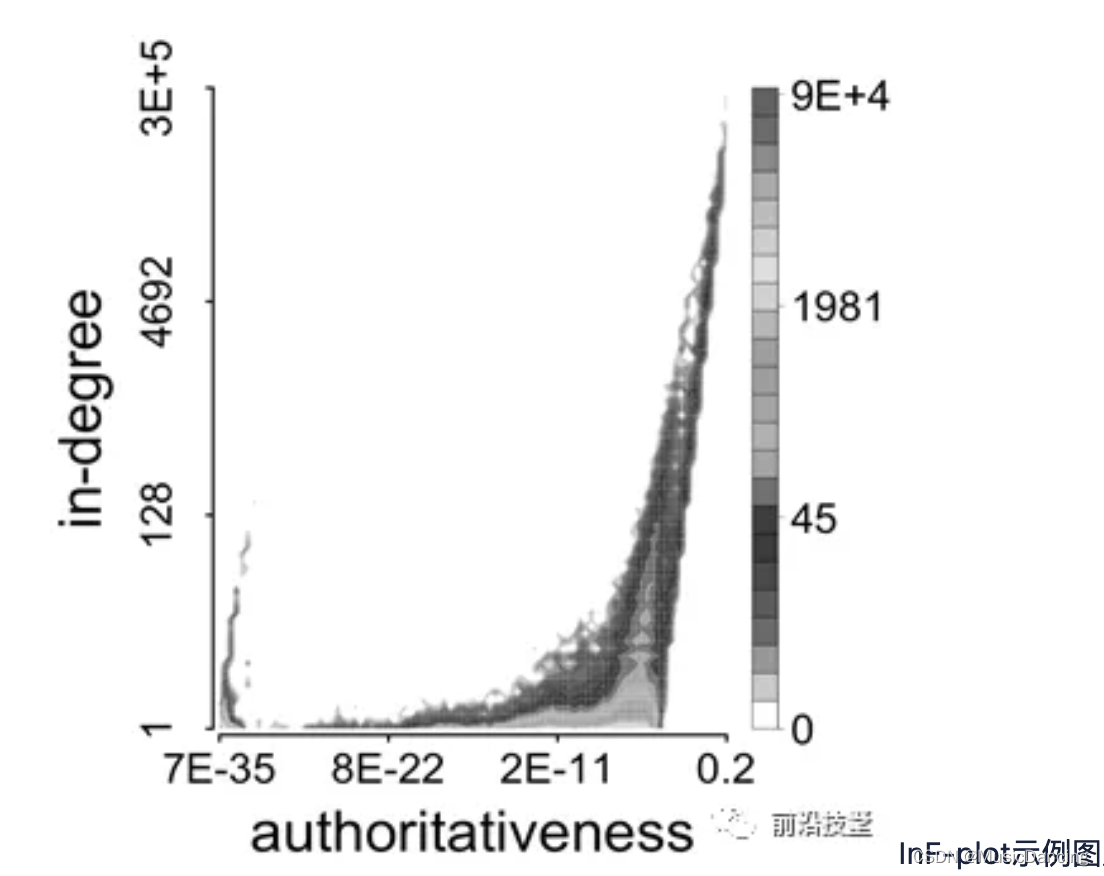
FRAUDARCatchSync算法简介
参考:https://blog.51cto.com/u_15127663/2778705 1. 背景 Fraudar 要解决的问题是:找出社交网络中最善于伪装的虚假用户簇。虚假用户会通过增加和正常用户的联系来进行伪装,而这些伪装(边)会形成一个很密集的子网络,可以通过定义…...
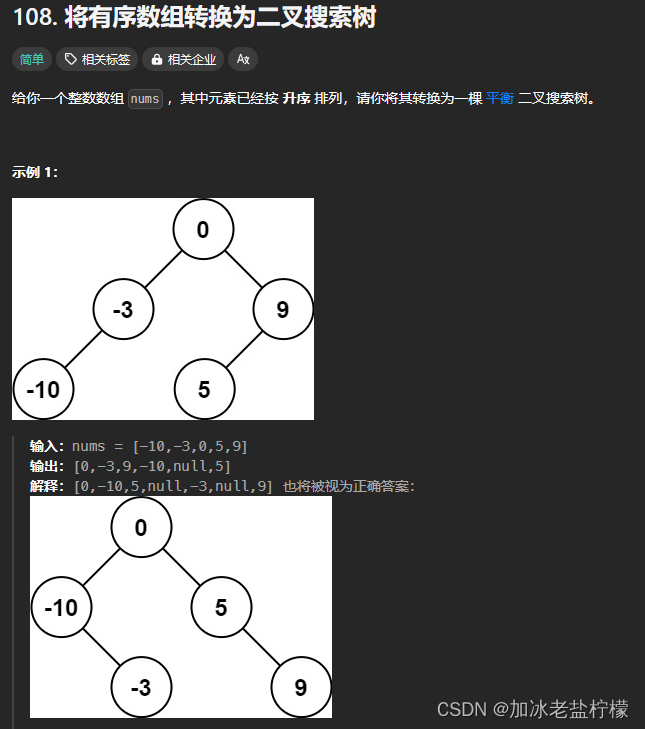
刷题之将有序数组转换成二叉搜索树(leetcode)
将有序数组转换成二叉搜索树 正常递归,中序遍历 递归经常会把自己绕晕,还是得画图分析 /*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(null…...
)
K-means聚类模型教程(个人总结版)
K-means聚类是一种广泛应用于数据挖掘和数据分析的无监督学习算法。它通过将数据点分成K个簇(cluster),使得同一簇内的数据点之间的相似度最大,不同簇之间的相似度最小。本文将详细介绍K-means聚类算法的背景、基本原理、具体实现…...

android怎么告诉系统不要回收
在Android中,如果你想告诉系统不要回收你的应用程序,可以通过设置Activity的属性来实现。你可以设置android:configChanges属性,指定在哪些配置更改时不重新创建Activity。 例如,如果你想指示系统在屏幕方向更改时不要重新创建Ac…...
)
【FAQ】HarmonyOS SDK 闭源开放能力 —IAP Kit(2)
1.问题描述: 应用内支付IAP Kit和Payment Kit的区别以及适用场景? 解决方案: IAP Kit是四方支付,仅支持在线虚拟商品,如会员,游戏钻石等,双框架支持全球,目前单框架暂时只支持国内…...
ubuntu设置root开机登录,允许root用户ssh远程登录
ubuntu与centos系统不同,默认root开机不能登录。 1、输入一下命令创建root密码,根据提示输入新密码 sudo passwd root 2、打开gdm-autologin文件,将auth required pam_succeed_if.so user ! root quiet_success这行注释掉,这行就…...
)
Web测试面试题(二)
一:简述HTTP协议的状态码包含哪些? 2XX,表示成功 3XX,表示重定向 4XX,表示客户端错误 5XX,表示服务器错误 二:HTTP和HTTPS的区别? 《1》安全性上的区别: HTTPS&#x…...

VBA宏指令写的方法突然不能用了
背景:项目组有个自动化测试项目,实在excel中利用VBA开发的;时间比较久远,我前面的哥们走后,这个软件一直在用,最近系统不知道是不是更新的缘故;有些代码除了问题; 先上源码: Dim Conn As Object, Rst As Object Dim sqlStr$ Dim str_start_SN$, str2$ str_start_SN …...

第13章 Python建模库介绍
以下内容参考自https://github.com/iamseancheney/python_for_data_analysis_2nd_chinese_version/blob/master/%E7%AC%AC05%E7%AB%A0%20pandas%E5%85%A5%E9%97%A8.md 《利用Python进行数据分析第2版》 用以学习和记录。 本书中,我已经介绍了Python数据分析的编程基…...
IP学习——ospf1
OSPF:开放式最短路径优先协议 无类别IGP协议:链路状态型。基于 LSA收敛,故更新量较大,为在中大型网络正常工作,需要进行结构化的部署---区域划分、ip地址规划 支持等开销负载均衡 组播更新 ---224.0.0.5 224.0.0.6 …...
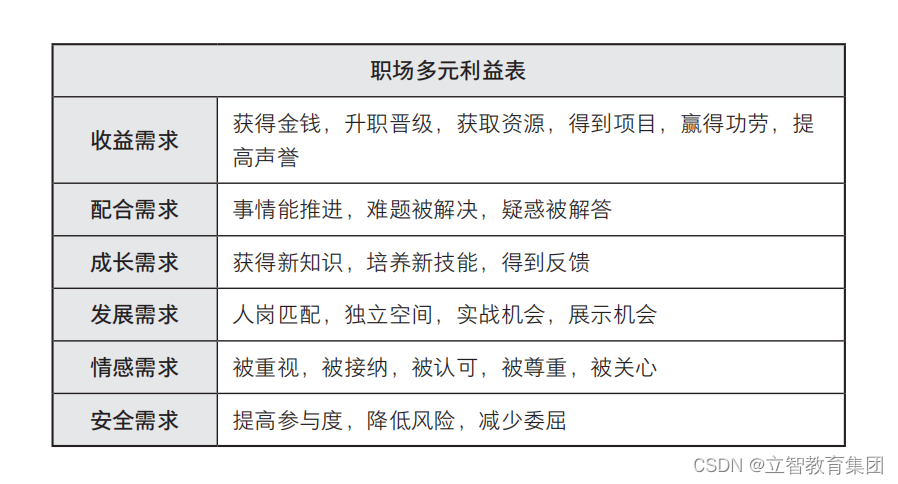
别说废话!说话说到点上,项目高效沟通的底层逻辑揭秘
假设你下周要在领导和同事面前汇报项目进度,你会怎么做?很多人可能会去网上搜一个项目介绍模板,然后按照模板来填充内容。最后,汇报幻灯片做了 80 页,自己觉得非常充实,但是却被领导痛批了一顿。 这样的境…...

前后端编程语言和运行环境的理解
我已重新检查了我的回答,并确保信息的准确性。以下是常用的编程语言,以及它们通常用于前端或后端开发,以及相应的框架和运行环境: 前端开发 JavaScript 框架:React, Angular, Vue.js, Ember.js, Backbone.js运行环境:Web 浏览器HTML (HyperText Markup Language) 不是编…...
一顿五元钱的午餐
在郑州喧嚣的城市一隅,藏着一段鲜为人知的真实的故事。 故事的主角是一位年过半百的父亲,一位平凡而又伟大的劳动者。岁月在他脸上刻下了深深的痕迹,但他眼神中闪烁着不屈与坚韧。 他今年52岁,为了给远在家乡的孩子们一个更好的…...

【前端每日基础】day60——TDK三大标签及SEO引擎优化
TDK 是指 Title(标题)、Description(描述)、Keywords(关键词)这三个网页的重要元信息标签,对于 SEO(搜索引擎优化)至关重要。下面是它们的作用和 SEO 优化建议࿱…...
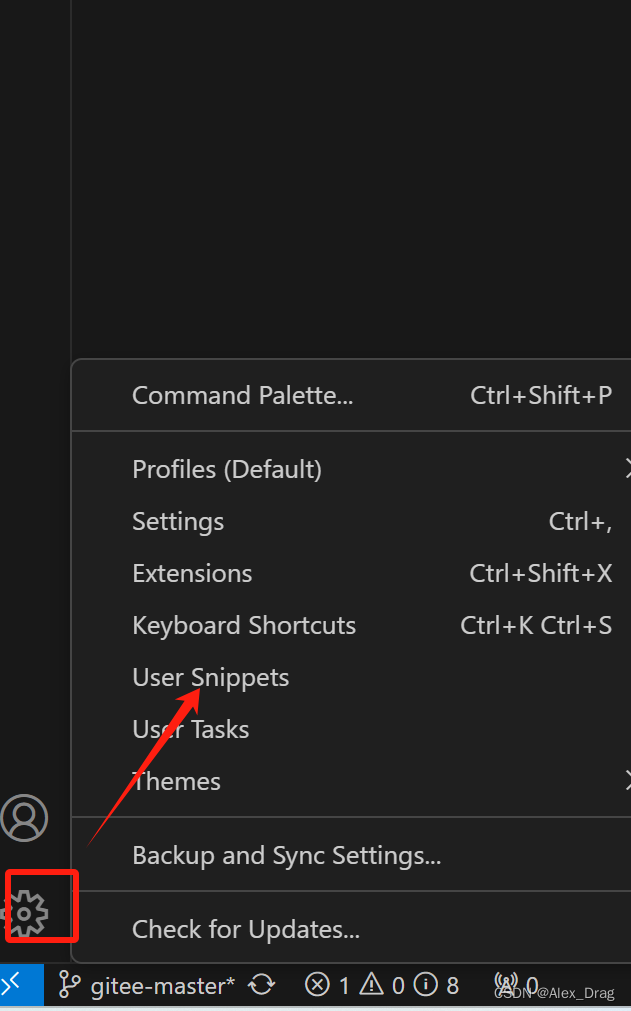
vscode添加代办相关插件,提高开发效率
这里写目录标题 前言插件添加添加TODO Highlight安装TODO Highlight在项目中自定义需要高亮显示的关键字 TODO Tree安装TODO Tree插件 单行注释快捷键 前言 在前端开发中,我们经常会遇到一些未完成、有问题或需要修复的部分,但又暂时未完成或未确定如何处…...
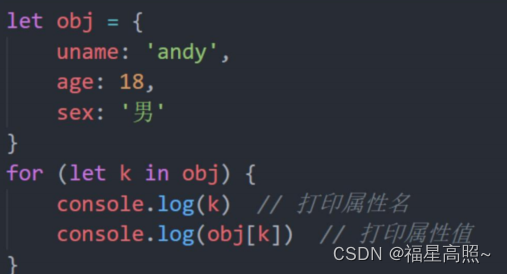
JS对象超细
目录 一、对象是什么 1.对象声明语法 2.对象有属性和方法组成 二、对象的使用 1.对象的使用 (1)查 (2)改 (3)增 (4)删(了解) (5…...
远程PLC、工控设备异地调试,贝锐蒲公英异地组网方案简单高效
北京宇东宁科技有限公司专门提供非标机电设备,能够用于金属制品的加工制造。设备主要采用西门子的PLC作为控制系统,同时能够连接上位机用于产量、温度、压力、电机运行数据的监控,以及工厂的大屏呈现需求。目前,客户主要是市场上的…...

【算法】梦破碎之地---三数之和
相信大家都有做过两数之和, 题目链接: 15. 三数之和 - 力扣(LeetCode) 在文章的开始让我们回顾一下三数之和吧! 题目描述: 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], …...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...
