K-means聚类模型教程(个人总结版)
K-means聚类是一种广泛应用于数据挖掘和数据分析的无监督学习算法。它通过将数据点分成K个簇(cluster),使得同一簇内的数据点之间的相似度最大,不同簇之间的相似度最小。本文将详细介绍K-means聚类算法的背景、基本原理、具体实现步骤、算法优化方法、优劣势以及应用实例。
一、算法背景
1.1 聚类分析的历史
聚类分析是一种重要的数据分析技术,可以追溯到20世纪50年代。其目的是将数据集分成若干个簇,使得同一个簇内的数据点尽可能相似,不同簇的数据点尽可能不同。聚类分析在许多领域有广泛应用,如模式识别、图像分析、市场研究、生物信息学等。
1.2 K-means算法的提出
K-means算法最早由Hugo Steinhaus在1956年提出,并由Stuart Lloyd在1957年进一步发展。其核心思想是通过迭代优化,使得每个数据点所属的簇中心与其距离最小,从而实现数据的聚类。
二、K-means聚类的基本原理
K-means聚类算法的目标是通过最小化簇内数据点到簇中心(centroid)的平方距离,使得每个簇内的数据点尽可能接近簇中心。具体步骤如下:
- 选择K个初始簇中心。
- 分配数据点到最近的簇中心。
- 重新计算簇中心:对于每个簇,计算其所有数据点的平均值,作为新的簇中心。
- 重复步骤2和步骤3,直到簇中心不再变化或达到预定的迭代次数。
三、K-means聚类的具体实现步骤
3.1 数据准备
在开始聚类之前,需要准备数据集。假设我们有一个二维数据集,每个数据点有两个特征。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs# 生成示例数据
X, y = make_blobs(n_samples=300, centers=4, random_state=42, cluster_std=0.60)# 可视化数据
plt.scatter(X[:, 0], X[:, 1], s=50)
plt.show()
3.2 选择初始簇中心
初始化K个簇中心可以随机选择数据点或使用其他初始化方法(如K-means++)。
def initialize_centroids(X, k):indices = np.random.choice(X.shape[0], k, replace=False)return X[indices]# 初始化簇中心
k = 4
centroids = initialize_centroids(X, k)
print("Initial centroids:\n", centroids)
3.3 分配数据点到最近的簇中心
计算每个数据点到所有簇中心的距离,并将其分配到最近的簇中心。
def assign_clusters(X, centroids):distances = np.sqrt(((X - centroids[:, np.newaxis])**2).sum(axis=2))return np.argmin(distances, axis=0)# 分配数据点到最近的簇中心
labels = assign_clusters(X, centroids)
print("Initial cluster assignments:\n", labels)
3.4 重新计算簇中心
根据分配结果,计算每个簇的新中心。
def compute_centroids(X, labels, k):return np.array([X[labels == i].mean(axis=0) for i in range(k)])# 重新计算簇中心
new_centroids = compute_centroids(X, labels, k)
print("New centroids:\n", new_centroids)
3.5 迭代步骤
重复分配数据点和重新计算簇中心,直到簇中心不再变化或达到最大迭代次数。
def kmeans(X, k, max_iters=100):centroids = initialize_centroids(X, k)for _ in range(max_iters):labels = assign_clusters(X, centroids)new_centroids = compute_centroids(X, labels, k)if np.all(centroids == new_centroids):breakcentroids = new_centroidsreturn centroids, labels# 运行K-means聚类
centroids, labels = kmeans(X, k)
print("Final centroids:\n", centroids)# 可视化聚类结果
plt.scatter(X[:, 0], X[:, 1], c=labels, s=50, cmap='viridis')
plt.scatter(centroids[:, 0], centroids[:, 1], s=200, c='red', marker='X')
plt.show()
四、K-means聚类的优化方法
4.1 K-means++初始化
K-means++是一种改进的初始化方法,通过更好地选择初始簇中心,减少了K-means的收敛时间,提高了结果的稳定性。
from sklearn.cluster import KMeans# 使用K-means++初始化
kmeans = KMeans(n_clusters=k, init='k-means++', max_iter=300, n_init=10, random_state=42)
y_kmeans = kmeans.fit_predict(X)# 可视化结果
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=200, c='red', marker='X')
plt.show()
4.2 确定最佳簇数
使用肘部法或轮廓系数等方法,可以帮助确定数据的最佳簇数。
4.2.1 肘部法
肘部法通过计算不同簇数下的总误差平方和(SSE),选择SSE下降速度减缓的点作为最佳簇数。
sse = []
for k in range(1, 11):kmeans = KMeans(n_clusters=k, init='k-means++', max_iter=300, n_init=10, random_state=42)kmeans.fit(X)sse.append(kmeans.inertia_)# 可视化肘部法
plt.plot(range(1, 11), sse, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('SSE')
plt.show()
4.2.2 轮廓系数
轮廓系数通过计算簇内和簇间的距离,评估不同簇数下的聚类效果。
from sklearn.metrics import silhouette_scoresilhouette_scores = []
for k in range(2, 11):kmeans = KMeans(n_clusters=k, init='k-means++', max_iter=300, n_init=10, random_state=42)y_kmeans = kmeans.fit_predict(X)silhouette_scores.append(silhouette_score(X, y_kmeans))# 可视化轮廓系数
plt.plot(range(2, 11), silhouette_scores, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Silhouette Score')
plt.show()
五、K-means聚类的优劣势
5.1 优势
- 简单易懂:K-means算法的基本思想简单直观,易于理解和实现。
- 计算效率高:对于大规模数据集,K-means算法的计算效率较高,适合快速聚类。
- 结果解释性强:聚类结果易于解释,可以直接通过簇中心和簇内数据点之间的关系进行分析。
5.2 劣势
- 对初始值敏感:K-means算法对初始簇中心的选择非常敏感,不同的初始值可能导致不同的聚类结果。
- 需要预先确定K值:K-means算法需要预先指定簇的数量K,这在实际应用中可能不容易确定。
- 对噪声和异常值敏感:K-means算法对数据中的噪声和异常值较为敏感,可能影响聚类结果的准确性。
- 适用数据类型有限:K-means算法主要适用于数值型数据,对于类别型数据或高维稀疏数据的效果不佳。
六、K-means聚类的应用实例
6.1 图像压缩
K-means聚类可以用于图像压缩,将图像像素分配到K个簇,从而减少颜色数量,实现图像压缩。
from skimage import io
from sklearn.utils import shuffle# 加载图像
image = io.imread('path/to/your/image.jpg')
image = np.array(image, dtype=np.float64) / 255# 将图像像素展开为二维数组
w, h, d = image.shape
image_array = np.reshape(image, (w * h, d))# 使用K-means进行图像压缩
k = 16
image_array_sample = shuffle(image_array, random_state=42)[:1000]
kmeans = KMeans(n_clusters=k, random_state=42).fit(image_array_sample)
labels = kmeans.predict(image_array)
compressed_image = kmeans.cluster_centers_[labels].reshape(w, h, d)# 显示压缩后的图像
plt.imshow(compressed_image)
plt.show()
6.2 客户细分
K-means聚类可以用于客户细分,根据客户的购买行为、人口统计数据等,将客户分成不同的簇,帮助企业进行精准营销。
import pandas as pd# 加载客户数据
data = pd.read_csv('path/to/your/customer_data.csv')# 选择特征进行聚类
X = data[['Annual Income (k$)', 'Spending Score (1-100)']]# 使用K-means进行客户细分
kmeans = KMeans(n_clusters=5, random_state=42)
y_kmeans = kmeans.fit_predict(X)# 可视化客户细分结果
plt.scatter(X.iloc[:, 0], X.iloc[:, 1], c=y_kmeans, s=50, cmap='viridis')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=200, c='red', marker='X')
plt.xlabel('Annual Income (k$)')
plt.ylabel('Spending Score (1-100)')
plt.show()
七、总结
K-means聚类是一种简单高效的无监督学习算法,广泛应用于图像处理、市场营销、客户细分等领域。通过详细介绍K-means聚类的基本原理、具体实现步骤、算法优化方法和应用实例,希望能帮助读者更好地理解和应用这一重要的机器学习技术。在实际应用中,选择合适的簇数和初始化方法,并结合具体问题的需求进行调整和优化,将有助于获得更好的聚类效果。
参考文献
为了深入理解和应用K-means聚类算法,建议参考以下资料:
- 《机器学习》 - 周志华
- 《模式分类》 - Duda, Hart, Stork
- 《数据挖掘:概念与技术》 - Han, Kamber, Pei
- K-means++: The Advantages of Careful Seeding - Arthur, Vassilvitskii (2007)
- A Comparison of the K-means and K-medoids Algorithms - Park, Jun (2009)
这些资料将提供更深入的理论背景和实践指南,帮助读者进一步掌握K-means聚类算法及其应用。
相关文章:
)
K-means聚类模型教程(个人总结版)
K-means聚类是一种广泛应用于数据挖掘和数据分析的无监督学习算法。它通过将数据点分成K个簇(cluster),使得同一簇内的数据点之间的相似度最大,不同簇之间的相似度最小。本文将详细介绍K-means聚类算法的背景、基本原理、具体实现…...

android怎么告诉系统不要回收
在Android中,如果你想告诉系统不要回收你的应用程序,可以通过设置Activity的属性来实现。你可以设置android:configChanges属性,指定在哪些配置更改时不重新创建Activity。 例如,如果你想指示系统在屏幕方向更改时不要重新创建Ac…...
)
【FAQ】HarmonyOS SDK 闭源开放能力 —IAP Kit(2)
1.问题描述: 应用内支付IAP Kit和Payment Kit的区别以及适用场景? 解决方案: IAP Kit是四方支付,仅支持在线虚拟商品,如会员,游戏钻石等,双框架支持全球,目前单框架暂时只支持国内…...
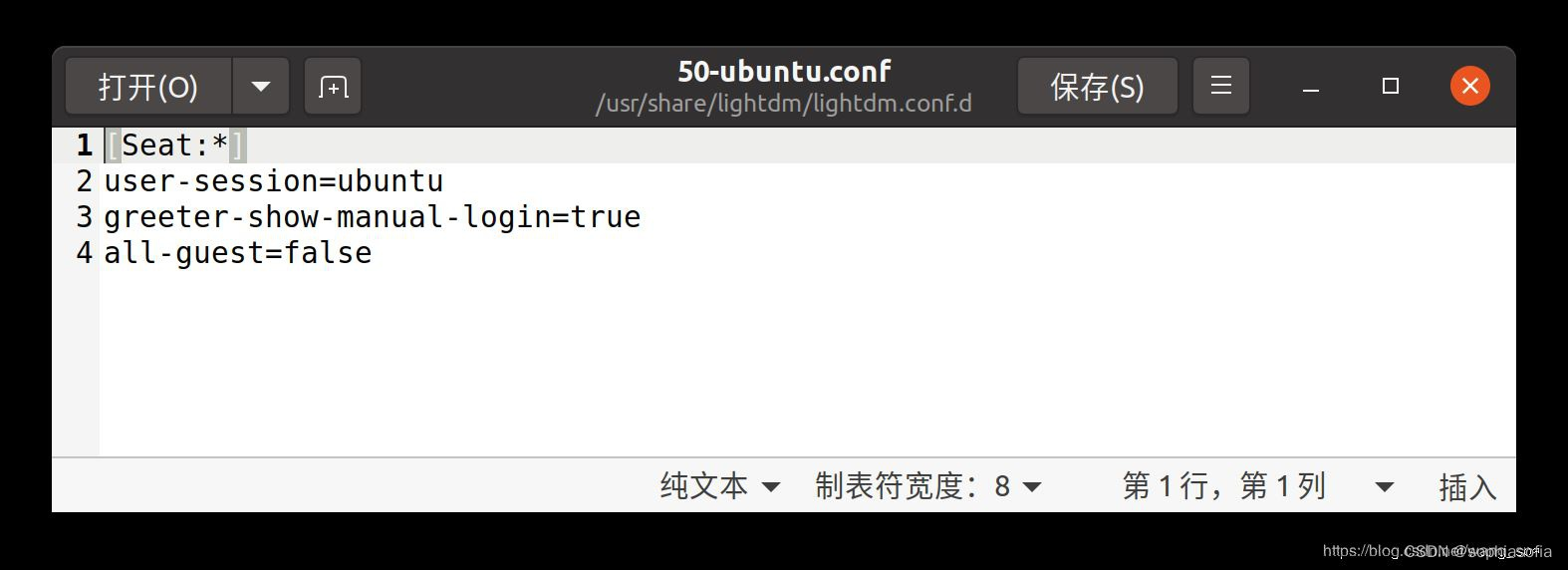
ubuntu设置root开机登录,允许root用户ssh远程登录
ubuntu与centos系统不同,默认root开机不能登录。 1、输入一下命令创建root密码,根据提示输入新密码 sudo passwd root 2、打开gdm-autologin文件,将auth required pam_succeed_if.so user ! root quiet_success这行注释掉,这行就…...
)
Web测试面试题(二)
一:简述HTTP协议的状态码包含哪些? 2XX,表示成功 3XX,表示重定向 4XX,表示客户端错误 5XX,表示服务器错误 二:HTTP和HTTPS的区别? 《1》安全性上的区别: HTTPS&#x…...

VBA宏指令写的方法突然不能用了
背景:项目组有个自动化测试项目,实在excel中利用VBA开发的;时间比较久远,我前面的哥们走后,这个软件一直在用,最近系统不知道是不是更新的缘故;有些代码除了问题; 先上源码: Dim Conn As Object, Rst As Object Dim sqlStr$ Dim str_start_SN$, str2$ str_start_SN …...

第13章 Python建模库介绍
以下内容参考自https://github.com/iamseancheney/python_for_data_analysis_2nd_chinese_version/blob/master/%E7%AC%AC05%E7%AB%A0%20pandas%E5%85%A5%E9%97%A8.md 《利用Python进行数据分析第2版》 用以学习和记录。 本书中,我已经介绍了Python数据分析的编程基…...
IP学习——ospf1
OSPF:开放式最短路径优先协议 无类别IGP协议:链路状态型。基于 LSA收敛,故更新量较大,为在中大型网络正常工作,需要进行结构化的部署---区域划分、ip地址规划 支持等开销负载均衡 组播更新 ---224.0.0.5 224.0.0.6 …...
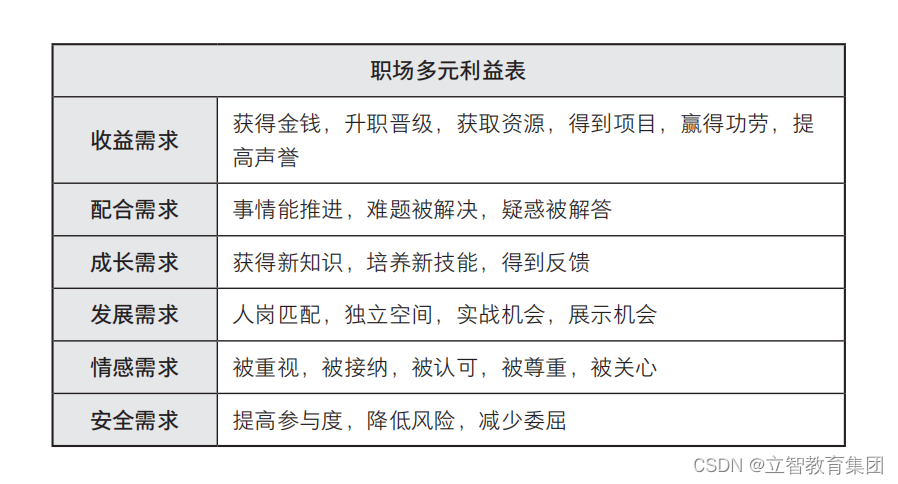
别说废话!说话说到点上,项目高效沟通的底层逻辑揭秘
假设你下周要在领导和同事面前汇报项目进度,你会怎么做?很多人可能会去网上搜一个项目介绍模板,然后按照模板来填充内容。最后,汇报幻灯片做了 80 页,自己觉得非常充实,但是却被领导痛批了一顿。 这样的境…...

前后端编程语言和运行环境的理解
我已重新检查了我的回答,并确保信息的准确性。以下是常用的编程语言,以及它们通常用于前端或后端开发,以及相应的框架和运行环境: 前端开发 JavaScript 框架:React, Angular, Vue.js, Ember.js, Backbone.js运行环境:Web 浏览器HTML (HyperText Markup Language) 不是编…...
一顿五元钱的午餐
在郑州喧嚣的城市一隅,藏着一段鲜为人知的真实的故事。 故事的主角是一位年过半百的父亲,一位平凡而又伟大的劳动者。岁月在他脸上刻下了深深的痕迹,但他眼神中闪烁着不屈与坚韧。 他今年52岁,为了给远在家乡的孩子们一个更好的…...

【前端每日基础】day60——TDK三大标签及SEO引擎优化
TDK 是指 Title(标题)、Description(描述)、Keywords(关键词)这三个网页的重要元信息标签,对于 SEO(搜索引擎优化)至关重要。下面是它们的作用和 SEO 优化建议࿱…...
vscode添加代办相关插件,提高开发效率
这里写目录标题 前言插件添加添加TODO Highlight安装TODO Highlight在项目中自定义需要高亮显示的关键字 TODO Tree安装TODO Tree插件 单行注释快捷键 前言 在前端开发中,我们经常会遇到一些未完成、有问题或需要修复的部分,但又暂时未完成或未确定如何处…...
JS对象超细
目录 一、对象是什么 1.对象声明语法 2.对象有属性和方法组成 二、对象的使用 1.对象的使用 (1)查 (2)改 (3)增 (4)删(了解) (5…...
远程PLC、工控设备异地调试,贝锐蒲公英异地组网方案简单高效
北京宇东宁科技有限公司专门提供非标机电设备,能够用于金属制品的加工制造。设备主要采用西门子的PLC作为控制系统,同时能够连接上位机用于产量、温度、压力、电机运行数据的监控,以及工厂的大屏呈现需求。目前,客户主要是市场上的…...

【算法】梦破碎之地---三数之和
相信大家都有做过两数之和, 题目链接: 15. 三数之和 - 力扣(LeetCode) 在文章的开始让我们回顾一下三数之和吧! 题目描述: 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], …...

c语言如何将一个文本内容复制到另外一个文本里
c语言如果要把一个文本文件的文件复制到另外一个文件里,代码如下 #include<stdio.h>int main() {FILE *fp1,*fp2;char a;fp1fopen("D://cyy//aaa.txt","r");fp2fopen("ccc.cpu","w");while(a!EOF){afgetc(fp1);fput…...
JavaScript基础(九)
冒泡排序 用例子比较好理解: var arry[7,2,6,3,4,1,8]; //拿出第一位数7和后面依次比较,遇到大的8就换位,8再与后面依次比较,没有能和8换位的数,再从下一位2依次与下面的数比较。 console.log(排列之前:arry); for (…...

决策树最优属性选择
本文以西瓜数据集为例演示决策树使用信息增益选择最优划分属性的过程 西瓜数据集下载:传送门 首先计算根节点的信息熵: 数据集分为好瓜、坏瓜,所以|y|2根结点包含17个训练样例,其中好瓜共计8个样例,所占比例为8/17坏…...

NER 数据集格式转换
NER 数据集格式 格式一 某些地方的数据和标签拆成两个文件了 sentences.txt 如 何 解 决 足 球 界 长 期 存 在 的 诸 多 矛 盾 , 重 振 昔 日 津 门 足 球 的 雄 风 , 成 为 天 津 足 坛 上 下 内 外 到 处 议 论 的 话 题 。 该 县 一 手 抓 农 业…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...
