在排序数组中查找元素的一个位置和最后一个位置-力扣
第一此次想到的解法是首先使用二分查找在排序数组中查找到一个指定元素,随后对该元素左右进行遍历,找到起始位置和结束位置,代码如下:
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {int size = nums.size();int min = 0;int max = size - 1;while(min <= max){int mid = min + (max - min)/2;if(target < nums[mid]){max = mid - 1;}else if(target > nums[mid]){min = mid + 1;}else{while(nums[min] != target){min++;}while(nums[max] != target){max--;}return {min,max};}}return {-1,-1};}
};
执行虽然通过,但测试用时并不是很理想,在 代码随想录 看到的解法是将题目分为三种情况:
- 情况一:target 在数组范围的右边或者左边,例如数组{3, 4, 5},target为2或者数组{3, 4, 5},target为6,此时应该返回{-1, -1}
- 情况二:target 在数组范围中,且数组中不存在target,例如数组{3,6,7},target为5,此时应该返回{-1, -1}
- 情况三:target 在数组范围中,且数组中存在target,例如数组{3,6,7},target为6,此时应该返回{1, 1}
采用二分法来分别寻找左边界和右边界,最终分情况进行return。代码如下:
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {int leftBorder = getLeftBorder(nums, target);int rightBorder = getRightBorder(nums, target);// 情况一if (leftBorder == -2 || rightBorder == -2) return {-1, -1};// 情况三if (rightBorder - leftBorder > 1) return {leftBorder + 1, rightBorder - 1};// 情况二return {-1, -1};}
private:int getRightBorder(vector<int>& nums, int target) {int left = 0;int right = nums.size() - 1;int rightBorder = -2; // 记录一下rightBorder没有被赋值的情况while (left <= right) {int middle = left + ((right - left) / 2);if (nums[middle] > target) {right = middle - 1;} else { // 寻找右边界,nums[middle] == target的时候更新leftleft = middle + 1;rightBorder = left;}}return rightBorder;}int getLeftBorder(vector<int>& nums, int target) {int left = 0;int right = nums.size() - 1;int leftBorder = -2; // 记录一下leftBorder没有被赋值的情况while (left <= right) {int middle = left + ((right - left) / 2);if (nums[middle] >= target) { // 寻找左边界,nums[middle] == target的时候更新rightright = middle - 1;leftBorder = right;} else {left = middle + 1;}}return leftBorder;}
};
将上述代码的两个二分查找函数进行合并:
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {int leftBorder = getBorder(nums, target, true);int rightBorder = getBorder(nums, target, false);// 情况一if (leftBorder == -2 || rightBorder == -2) return {-1, -1};// 情况三if (rightBorder - leftBorder > 1) return {leftBorder + 1, rightBorder - 1};// 情况二return {-1, -1};}
private:int getBorder(vector<int>& nums, int target, bool flag) {int left = 0;int right = nums.size() - 1;int border = -2;while (left <= right){int middle = left + (right - left)/2;if(flag) { //flag = true,返回左边界if (nums[middle] >= target) { // 寻找左边界,nums[middle] == target的时候更新rightright = middle - 1;border = right;} else {left = middle + 1;}}else{if (nums[middle] > target) {right = middle - 1;} else { // 寻找右边界,nums[middle] == target的时候更新leftleft = middle + 1;border = left;}}}return border;}};
相关文章:

在排序数组中查找元素的一个位置和最后一个位置-力扣
第一此次想到的解法是首先使用二分查找在排序数组中查找到一个指定元素,随后对该元素左右进行遍历,找到起始位置和结束位置,代码如下: class Solution { public:vector<int> searchRange(vector<int>& nums, int…...

系统分析师-案例分析-数据库
系统分析师-案例分析-数据库 更多软考资料 https://ruankao.blog.csdn.net/ 文章目录 系统分析师-案例分析-数据库数据库考察知识点规范化函数依赖范式1NF2NF3NF 规范化问题不规范化反规范化设计反规范化设计同步问题 并发控制性能优化完整性约束视图安全分布式数据库特点优点…...

【RabbitMQ】使用SpringAMQP的消息队列(Hello Word)和工作队列(Work Queue)
SpringAMQP SpringAMQP中文文档 Hello Word **案例1:**利用SpringAMQP实现HelloWord中的集成消息队列功能 项目结构,如图: 1.引入AMQP依赖(父工程中) <!--AMQP依赖,包含RabbitMQ--> <dependen…...
项目集成SkyWalking,基于k8s搭建
一、搭建SkyWalking 官方文档(英文):skywalking/docs at master apache/skywalking 中文可以使用:GitHub - SkyAPM/document-cn-translation-of-skywalking: [已过期,请使用官网AI文档] The CN translation version of Apache…...

mysql-差异备份流程
4.差异备份流程 差异备份流程(重要) 第一次完整备份 innobackupex /xtrabackup innobackupex --userroot --password123456 /xtrabackup2024-05-23_20-25-05 第一次完整备份 2024-05-23_20-40-55 第二次差异备份 2024-05-23_20-47-37 第三次差异备份再往数据库里面…...
的打分矩阵)
基于动态规划算法的DNA序列比对函数,给出两条序列(v和w)的打分矩阵
一.什么是动态规划算法 1.1总体思想 动态规划算法与分治法类似,基本思想也是将待求解的问题分成若干个子问题 经过分解得到的子问题往往不是互相独立的,有些子问题被重复计算多次 如果能够保存已解决的子问题答案,在需要时再找出来已求得…...

Tailwind CSS快速入门
文章目录 初识安装Tailwindcss试用安装快速书写技巧扩展好处Todo 初识 只需书写 HTML 代码,无需书写 CSS,即可快速构建美观的网站 Tailwind CSS 是一个功能类优先的 CSS 框架,它通过提供大量的原子类(utility classes)…...
Postman使用技巧
Postman是一款广泛使用的API开发和测试工具,专为简化Web服务API的开发、测试、文档编制和协作过程而设计。它支持各种HTTP请求方法,包括GET、POST、PUT、DELETE等,允许用户轻松地构建和发送请求,以及检查响应。 本文介绍几个提升效…...

sqli-labs靶场
less---11 1.求闭合字符 输入1报错说明存在注入点 存在注入点 2.查库名 使用报错注入查库名 admin” and (select 1 from (select count(*),concat(database(),floor(rand(0)*2))x from information_schema.tables group by x)y)# //floor函数报错 3.查表名 admin and upd…...

基于springboot的大创管理系统
摘要 随着信息技术在管理上越来越深入而广泛的应用,管理信息系统的实施在技术上已逐步成熟。本文介绍了大创管理系统的开发全过程。通过分析大创管理系统管理的不足,创建了一个计算机管理大创管理系统的方案。文章介绍了大创管理系统的系统分析部分&…...

常用torch.nn
目录 一、torch.nn和torch.nn.functional二、nn.Linear三、nn.Embedding四、nn.Identity五、Pytorch非线性激活函数六、nn.Conv2d七、nn.Sequential八、nn.ModuleList九、torch.outer torch.cat 一、torch.nn和torch.nn.functional Pytorch中torch.nn和torch.nn.functional的区…...

力扣226.翻转二叉树101.对称二叉树
解决二叉树的问题,经常要习惯从递归角度思考 左子树/右子树是否具备某属性、是否属于什么类型(和题目要求的判断当前树是否xxx一样); 对左/右子树进行什么操作(和题目要求的对当前树的操作一样)。 226.翻转…...
word如何按照原本页面审阅文档
1 视图-阅读视图 2 视图,自己看,懒得打字了哈哈...

前端基础入门三大核心之HTML篇:探索WebAssembly —— 开启网页高性能应用新时代
前端基础入门三大核心之HTML篇:探索WebAssembly —— 开启网页高性能应用新时代 WebAssembly基础概念工作原理概览WebAssembly实战示例基本使用 安全性与性能优化防范漏洞实践实际工作中的使用技巧结语与讨论 随着Web技术的飞速发展,前端开发者面临越来越…...
)
NDIS小端口驱动(四)
NDIS中断相关 1. 注册和取消注册中断: 微型端口驱动程序调用 NdisMRegisterInterruptEx 来注册中断。 驱动程序分配并初始化 NDIS_MINIPORT_INTERRUPT_CHARACTERISTICS 结构,以指定中断特征和函数入口点,驱动程序将结构传递给 NdisMRegister…...

用户态网络缓冲区设计
基于数组实现的环形缓冲区: 优点 使用固定大小的连续空间做用户态缓冲区,利用了内存访问的局部性,可以提高缓存命中率,提高程序性能,在处理大量数据时,缓存的利用率对性能有着很大的影响 正是基于性能的…...
)
Linux运维工程师基础面试题整理(三)
Linux运维工程师基础面试题整理(三) 1. 文件inode号有什么用?2. 文件的权限怎么设置与管理?3. 如何SSH免密配置?4. 如何快速部署一个web服务?5. 如何更新Linux系统内核?6. centos中如何配置本地yum源?7.Linux 防火墙如何简单配置?8. 有哪些工具可以批量管理Linux服务器…...
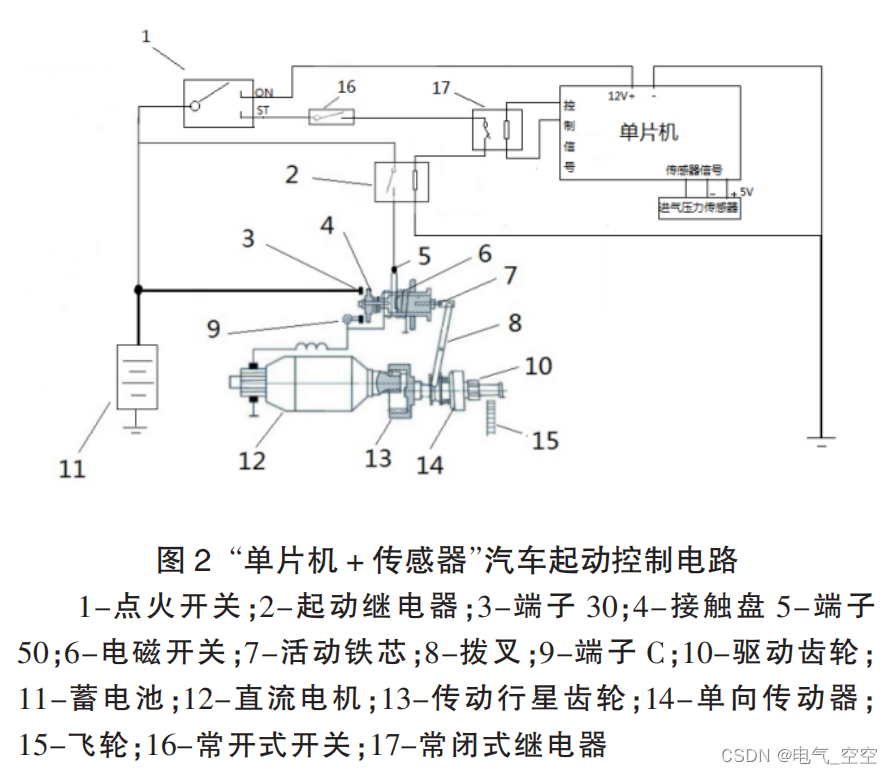
基于单片机与传感器技术的汽车起动线路设计
摘 要:在以发动机为动力源的汽车中,起动系统承担起使发动机由非工作状态进入工作状态的重要作用,属于发动机的附属系统。在传统汽车起动系统的基础上提出将单片机与传感器技术运用到起动控制线路中,通过传感器采集发动机工作状态信…...

C#如何通过反射获取外部dll的函数
在C#中,你可以使用反射(Reflection)来加载外部的DLL(动态链接库)并获取其中的函数(在C#中通常称为方法)。但是,请注意,反射主要用于访问类型信息,并且对于非托…...

从零开始傅里叶变换
从零开始傅里叶变换 1 Overview2 傅里叶级数2.1 基向量2.2 三角函数系表示 f ( t ) f(t) f(t)2.2.1 三角函数系的正交性2.2.2 三角函数系的系数 2.3 复指数函数系表示 f ( t ) f(t) f(t)2.3.1 复指数函数系的系数2.3.2 复指数函数系的正交性 2.4 傅里叶级数总结 3 傅里叶变换…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...
