从零开始傅里叶变换
从零开始傅里叶变换
- 1 Overview
- 2 傅里叶级数
- 2.1 基向量
- 2.2 三角函数系表示 f ( t ) f(t) f(t)
- 2.2.1 三角函数系的正交性
- 2.2.2 三角函数系的系数
- 2.3 复指数函数系表示 f ( t ) f(t) f(t)
- 2.3.1 复指数函数系的系数
- 2.3.2 复指数函数系的正交性
- 2.4 傅里叶级数总结
- 3 傅里叶变换
1 Overview
Motivation:从时域转换到频域。相当于提取了信号的频率特征,可以做进一步的处理和分析。


对于时域内的一个信号 f ( t ) f(t) f(t) ,可以通过傅里叶变换得到频域函数 F ( ω ) F(\omega) F(ω),同样也可以从频域转化为时域。
傅里叶变换:
F ( ω ) = ∫ − ∞ ∞ f ( t ) ⋅ e − i ω t d t F(\omega)=\int_{-\infty}^{\infty}f(t)\cdot e^{-i\omega t}\text{ d}t F(ω)=∫−∞∞f(t)⋅e−iωt dt
傅里叶逆变换:
f ( t ) = 1 2 π ∫ − ∞ ∞ F ( ω ) e i ω t d ω f(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty} F(\omega)e^{i\omega t} \text{ d} \omega f(t)=2π1∫−∞∞F(ω)eiωt dω
2 傅里叶级数
傅里叶级数:任意周期性函数(波形)都可以表示成多个正余弦函数的线性组合。
f ( t ) = a 0 2 + a 1 cos ( ω t ) + b 1 sin ( ω t ) + a 2 cos ( ω t ) + b 2 sin ( ω t ) + ⋯ = a 0 2 + ∑ n = 1 ∞ ( a n cos ( n ω t ) + b n sin ( n ω t ) ) \begin{align*} f(t)&=\frac{a_0}{2}+a_1\cos(\omega t)+b_1\sin(\omega t)+a_2\cos(\omega t)+b_2\sin(\omega t)+\cdots\\ &=\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\cos(n\omega t)+b_n \sin(n\omega t))\\ \end{align*} f(t)=2a0+a1cos(ωt)+b1sin(ωt)+a2cos(ωt)+b2sin(ωt)+⋯=2a0+n=1∑∞(ancos(nωt)+bnsin(nωt))
其中
a n = 2 T ∫ t 0 t o + T f ( t ) cos ( n ω t ) d t b n = 2 T ∫ t 0 t o + T f ( t ) sin ( n ω t ) d t a_n = \frac{2}{T} \int_{t_0}^{t_o+T}f(t)\cos(n\omega t)\text{d}t\\ b_n = \frac{2}{T} \int_{t_0}^{t_o+T}f(t)\sin(n\omega t)\text{d}t\\ an=T2∫t0to+Tf(t)cos(nωt)dtbn=T2∫t0to+Tf(t)sin(nωt)dt
2.1 基向量
为什么一个周期性函数(波形)可以表示成多个正余弦函数的线性组合?
-
Recall 空间中的基向量:
- M M M 维空间的任意一个向量都可以表示为该空间的基向量 Q = { q 1 , q 2 , ⋯ , q M } \mathbf Q=\{\mathbf q_1,\mathbf q_2,\cdots,\mathbf q_M\} Q={q1,q2,⋯,qM} 的线性组合: v = x 1 q 1 + x 2 q 2 + ⋯ + x M q M \mathbf v=x_1\mathbf q_1+x_2\mathbf q_2 + \cdots +x_M \mathbf q_M v=x1q1+x2q2+⋯+xMqM
- 这 M M M 个基向量两两正交: q i ⊤ q j = 0 , ( i ≠ j ) \mathbf q_i^\top\mathbf q_j=0,\ \ (i\ne j) qi⊤qj=0, (i=j)
-
Recall 正交函数:
-
将函数看作向量,连续函数也就是一个维度 M = ∞ M=\infty M=∞ 的向量。即一个在 [ a , b ] [a,b] [a,b] 上有定义的实函数 f ( x ) f(x) f(x) 可以表示为一个 M M M 维的向量 f \mathbf f f: f ( x ) = f = ( f ( a ) , f ( a + Δ x ) , f ( a + 2 Δ x ) , ⋯ , f ( a + ( M − 1 ) Δ x ) ) f(x)=\mathbf f = (f(a),f(a+\Delta x),f(a+2\Delta x),\cdots,f(a+(M-1)\Delta x)) f(x)=f=(f(a),f(a+Δx),f(a+2Δx),⋯,f(a+(M−1)Δx))。其中 Δ x → 0 \Delta x\to 0 Δx→0 且 b = a + ( M − 1 ) Δ x b=a+(M-1)\Delta x b=a+(M−1)Δx
-
根据上文中提到的
M M M 维空间的任意一个向量都可以表示为该空间的基向量 Q = { q 1 , q 2 , ⋯ , q M } \mathbf Q=\{\mathbf q_1,\mathbf q_2,\cdots,\mathbf q_M\} Q={q1,q2,⋯,qM} 的线性组合
那么 f \mathbf f f 可以由 M M M 个 M M M 维的正交向量表示(基向量),找到基向量 g 0 , g 1 , ⋯ , g M − 1 \mathbf g_0, \mathbf g_1,\cdots,\mathbf g_{M-1} g0,g1,⋯,gM−1 表示为函数 g 0 , g 1 , ⋯ , g M − 1 g_0,g_1,\cdots,g_{M-1} g0,g1,⋯,gM−1:
g 0 = g 0 ( x ) = ( g 0 ( a ) , g 0 ( a + Δ x ) , g 0 ( a + 2 Δ x ) , ⋯ , g 0 ( a + ( M − 1 ) Δ x ) ) g 1 = g 1 ( x ) = ( g 1 ( a ) , g 1 ( a + Δ x ) , g 1 ( a + 2 Δ x ) , ⋯ , g 1 ( a + ( M − 1 ) Δ x ) ) ⋯ g M − 1 = g M − 1 ( x ) = ( g M − 1 ( a ) , g M − 1 ( a + Δ x ) , g M − 1 ( a + 2 Δ x ) , ⋯ , g M − 1 ( a + ( M − 1 ) Δ x ) ) \begin{align*} \mathbf g_0 &= g_0(x)=(g_0(a),g_0(a+\Delta x),g_0(a+2\Delta x),\cdots,g_0(a+(M-1)\Delta x))\\ \mathbf g_1 &= g_1(x)=(g_1(a),g_1(a+\Delta x),g_1(a+2\Delta x),\cdots,g_1(a+(M-1)\Delta x))\\ & \cdots\\ \mathbf g_{M-1} &= g_{M-1}(x)=(g_{M-1}(a),g_{M-1}(a+\Delta x),g_{M-1}(a+2\Delta x),\cdots,g_{M-1}(a+(M-1)\Delta x))\\ \end{align*} g0g1gM−1=g0(x)=(g0(a),g0(a+Δx),g0(a+2Δx),⋯,g0(a+(M−1)Δx))=g1(x)=(g1(a),g1(a+Δx),g1(a+2Δx),⋯,g1(a+(M−1)Δx))⋯=gM−1(x)=(gM−1(a),gM−1(a+Δx),gM−1(a+2Δx),⋯,gM−1(a+(M−1)Δx))
可以得出 g 0 , g 1 , ⋯ , g M − 1 g_0,g_1,\cdots,g_{M-1} g0,g1,⋯,gM−1 是两两正交的函数,也就是: ∫ a b g i ( x ) g j ( x ) d x = 0 , ( i ≠ j ) \int_a^b g_i(x)g_j(x)\text{d}x=0,\ \ (i\ne j) ∫abgi(x)gj(x)dx=0, (i=j)那么 f \mathbf f f 可以由 g 0 , g 1 , ⋯ , g M − 1 g_0,g_1,\cdots,g_{M-1} g0,g1,⋯,gM−1 的线性组合来表示:
f ( x ) = f = a 0 g 0 ( x ) + a 1 g 1 ( x ) + ⋯ + a M − 1 g M − 1 ( x ) f(x)=\mathbf f=a_0g_0(x)+a_1g_1(x)+\cdots+a_{M-1}g_{M-1}(x) f(x)=f=a0g0(x)+a1g1(x)+⋯+aM−1gM−1(x)
为了求系数 a n a_n an,其中 n = 0 , ⋯ M − 1 n=0,\cdots M-1 n=0,⋯M−1,先在两边同时乘上 g n ( x ) g_n(x) gn(x),然后再对 x x x 积分
∫ a b f ( x ) g n ( x ) d x = ∫ a b ( a 0 g 0 ( x ) + a 1 g 1 ( x ) + ⋯ + a M − 1 g M − 1 ( x ) ) g n ( x ) d x = ∫ a b a 0 g 0 ( x ) g n ( x ) + a 1 g 1 ( x ) g n ( x ) + ⋯ a n g n ( x ) g n ( x ) + ⋯ + a M − 1 g M − 1 ( x ) g n ( x ) d x = ∫ a b 0 + 0 + ⋯ + a n g n ( x ) g n ( x ) + ⋯ + 0 d x = ∫ a b a n g n ( x ) g n ( x ) d x a n = ∫ a b f ( x ) g n ( x ) d x ∫ a b g n ( x ) g n ( x ) d x \begin{align*} \int_a^b f(x)g_n(x)\text{d} x&=\int_a^b (a_0g_0(x)+a_1g_1(x)+\cdots+a_{M-1}g_{M-1}(x))g_n(x) \text { d} x\\ &=\int_a^ba_0g_0(x)g_n(x)+a_1g_1(x)g_n(x)+\cdots a_ng_n(x)g_n(x)+\cdots+a_{M-1}g_{M-1}(x)g_n(x) \text { d} x\\ &=\int_a^b 0+0+\cdots +a_ng_n(x)g_n(x)+\cdots +0 \text { d} x\\ &=\int_a^b a_n g_n(x)g_n(x)\text { d} x\\ a_n&=\frac{\int_a^b f(x)g_n(x)\text d x}{\int_a^b g_n(x)g_n(x)\text { d} x} \end{align*} ∫abf(x)gn(x)dxan=∫ab(a0g0(x)+a1g1(x)+⋯+aM−1gM−1(x))gn(x) dx=∫aba0g0(x)gn(x)+a1g1(x)gn(x)+⋯angn(x)gn(x)+⋯+aM−1gM−1(x)gn(x) dx=∫ab0+0+⋯+angn(x)gn(x)+⋯+0 dx=∫abangn(x)gn(x) dx=∫abgn(x)gn(x) dx∫abf(x)gn(x)dx
-
2.2 三角函数系表示 f ( t ) f(t) f(t)
2.2.1 三角函数系的正交性
-
三角函数系 1 , cos ( ω t ) , sin ( ω t ) , cos ( 2 ω t ) , sin ( 2 ω t ) , ⋯ ⋯ , cos ( n ω t ) , sin ( n ω t ) , ⋯ ⋯ 1,\cos (\omega t),\sin (\omega t),\cos (2 \omega t),\sin (2 \omega t), \cdots \ \cdots,\cos (n\omega t), \sin (n\omega t), \cdots\ \cdots 1,cos(ωt),sin(ωt),cos(2ωt),sin(2ωt),⋯ ⋯,cos(nωt),sin(nωt),⋯ ⋯ 就是这样的一组在区间 [ t 1 , t 2 ] [t_1,t_2] [t1,t2] 内两两正交的函数,即上文中的 g 0 ( t ) , g 1 ( t ) , ⋯ , g M − 1 ( t ) g_0(t),g_1(t),\cdots,g_{M-1}(t) g0(t),g1(t),⋯,gM−1(t)。这里 ω = 2 π t 2 − t 1 \omega = \frac{2\pi}{t_2-t_1} ω=t2−t12π
-
证明三角函数系确实是两两正交的,这些三角函数可以分为五类: 1 , cos ( n ω t ) , cos ( m ω t ) , sin ( n ω t ) , sin ( m ω t ) 1,\cos (n\omega t), \cos (m\omega t),\sin (n\omega t), \sin (m\omega t) 1,cos(nωt),cos(mωt),sin(nωt),sin(mωt)。这里 n ≠ m n\ne m n=m 且 n , m = 1 , 2 , 3 ⋯ n,m=1,2,3\cdots n,m=1,2,3⋯ 即正整数。证明这五类两两正交即可
-
1 ⊥ cos ( n ω t ) : ∫ t 1 t 2 cos ( n ω t ) d t = 0 1 \ \ \bot \ \ \cos (n\omega t): \int_{t_1}^{t_2} \cos (n\omega t) \text { d} t=0 1 ⊥ cos(nωt):∫t1t2cos(nωt) dt=0
由于 ω = 2 π t 2 − t 1 \omega = \frac{2\pi}{t_2-t_1} ω=t2−t12π ,第 n n n 项三角函数 f trg n ( t ) = cos ( n ω t ) f^{n}_{\text{trg}}(t)=\cos(n\omega t) ftrgn(t)=cos(nωt) 的周期 T n = 2 π n ω = t 2 − t 1 n T_n=\frac{2\pi}{n\omega}=\frac{t_2-t_1}{n} Tn=nω2π=nt2−t1,可以得出 t 2 − t 1 = n T n t_2-t_1=nT_n t2−t1=nTn,即区间 [ t 1 , t 2 ] [t_1,t_2] [t1,t2] 是 cos ( n ω t ) \cos (n\omega t) cos(nωt) 的周期的整数倍,即 [ t 2 , t 1 ] [t_2,t_1] [t2,t1] 一定是 cos ( n ω t ) \cos (n\omega t) cos(nωt) 的一个周期,即可得出 ∫ t 1 t 2 cos ( n ω t ) d t = 0 \int_{t_1}^{t_2} \cos (n\omega t) \text { d} t=0 ∫t1t2cos(nωt) dt=0
-
1 ⊥ sin ( n ω t ) : ∫ t 1 t 2 sin ( n ω t ) d t = 0 1 \ \ \bot \ \ \sin (n\omega t): \int_{t_1}^{t_2} \sin (n\omega t) \text { d} t=0 1 ⊥ sin(nωt):∫t1t2sin(nωt) dt=0
类似的,通过区间 [ t 2 , t 1 ] [t_2,t_1] [t2,t1] 是 sin ( n ω t ) \sin (n\omega t) sin(nωt) 的一个周期,可以证明 ∫ t 1 t 2 sin ( n ω t ) d t = 0 \int_{t_1}^{t_2} \sin (n\omega t) \text { d} t=0 ∫t1t2sin(nωt) dt=0
-
sin ( n ω t ) ⊥ sin ( m ω t ) : ∫ t 1 t 2 sin ( n ω t ) sin ( m ω t ) d t = 0 \sin (n\omega t) \bot \sin (m\omega t): \int_{t_1}^{t_2}\sin (n \omega t) \sin (m\omega t) \text{ d}t=0 sin(nωt)⊥sin(mωt):∫t1t2sin(nωt)sin(mωt) dt=0
根据积化和差:
∫ t 1 t 2 sin ( n ω t ) sin ( m ω t ) d t = ∫ t 1 t 2 − 1 2 ( cos ( n + m ) ω t − cos ( n − m ) ω t ) d t = − 1 2 ∫ t 1 t 2 cos ( n ′ ω t ) − cos ( m ′ ω t d t ) = − 1 2 ( ∫ t 1 t 2 cos ( n ′ ω t ) d t − ∫ t 1 t 2 cos ( m ′ ω t ) d t ) = 0 \begin{align*} \int_{t_1}^{t_2} \sin (n \omega t) \sin (m\omega t) \text{ d}t&=\int_{t_1}^{t_2} -\frac{1}{2}(\cos(n+m)\omega t-\cos(n-m)\omega t)\text{ d} t\\ &=-\frac{1}{2}\int_{t_1}^{t_2} \cos (n'\omega t)-\cos (m' \omega t \text{ d} t)\\ &=-\frac{1}{2} \left ( \int_{t_1}^{t_2} \cos (n'\omega t)\text{ d} t-\int_{t_1}^{t_2}\cos (m' \omega t) \text{ d} t\right )\\ &=0 \end{align*} ∫t1t2sin(nωt)sin(mωt) dt=∫t1t2−21(cos(n+m)ωt−cos(n−m)ωt) dt=−21∫t1t2cos(n′ωt)−cos(m′ωt dt)=−21(∫t1t2cos(n′ωt) dt−∫t1t2cos(m′ωt) dt)=0 -
cos ( n ω t ) ⊥ cos ( m ω t ) : ∫ t 1 t 2 cos ( n ω t ) cos ( m ω t ) d t = 0 \cos (n \omega t) \bot \cos (m\omega t): \int_{t_1}^{t_2}\cos (n \omega t) \cos (m\omega t) \text{ d}t=0 cos(nωt)⊥cos(mωt):∫t1t2cos(nωt)cos(mωt) dt=0
类似地,根据积化和差:
∫ t 1 t 2 cos ( n ω t ) cos ( m ω t ) d t = ∫ t 1 t 2 1 2 ( cos ( n + m ) ω t + cos ( n − m ) ω t ) d t = 1 2 ∫ t 1 t 2 cos ( n ′ ω t ) + cos ( m ′ ω t ) d t = 1 2 ( ∫ t 1 t 2 cos ( n ′ ω t ) d t + ∫ t 1 t 2 cos ( m ′ ω t ) d t ) = 0 \begin{align*} \int_{t_1}^{t_2} \cos (n \omega t) \cos (m\omega t) \text{ d}t&=\int_{t_1}^{t_2} \frac{1}{2}(\cos(n+m)\omega t+\cos(n-m)\omega t)\text{ d} t\\ &=\frac{1}{2}\int_{t_1}^{t_2} \cos (n'\omega t)+\cos( m' \omega t) \text{ d} t\\ &=\frac{1}{2} \left ( \int_{t_1}^{t_2} \cos (n'\omega t)\text{ d} t+\int_{t_1}^{t_2}\cos (m' \omega t) \text{ d} t\right )\\ &=0 \end{align*} ∫t1t2cos(nωt)cos(mωt) dt=∫t1t221(cos(n+m)ωt+cos(n−m)ωt) dt=21∫t1t2cos(n′ωt)+cos(m′ωt) dt=21(∫t1t2cos(n′ωt) dt+∫t1t2cos(m′ωt) dt)=0 -
sin ( n ω t ) ⊥ cos ( m ω t ) : ∫ t 1 t 2 sin ( n ω t ) cos ( m ω t ) d t = 0 \sin (n \omega t) \bot \cos (m\omega t): \int_{t_1}^{t_2}\sin (n \omega t) \cos (m\omega t) \text{ d}t=0 sin(nωt)⊥cos(mωt):∫t1t2sin(nωt)cos(mωt) dt=0 ,此时无需 m ≠ n m\ne n m=n
由积化和差:
∫ t 1 t 2 sin ( n ω t ) cos ( m ω t ) d t = ∫ t 1 t 2 1 2 ( sin ( n + m ) ω t + sin ( n − m ) ω t ) d t = 1 2 ∫ t 1 t 2 sin ( n ′ ω t ) + sin ( m ′ ω t ) d t = 1 2 ( ∫ t 1 t 2 sin ( n ′ ω t ) d t + ∫ t 1 t 2 sin ( m ′ ω t ) d t ) = 0 \begin{align*} \int_{t_1}^{t_2} \sin (n \omega t) \cos (m\omega t) \text{ d}t&=\int_{t_1}^{t_2} \frac{1}{2}(\sin(n+m)\omega t+\sin(n-m)\omega t)\text{ d} t\\ &=\frac{1}{2}\int_{t_1}^{t_2} \sin (n'\omega t)+\sin (m' \omega t) \text{ d} t\\ &=\frac{1}{2} \left ( \int_{t_1}^{t_2} \sin (n'\omega t)\text{ d} t+\int_{t_1}^{t_2}\sin (m' \omega t) \text{ d} t\right )\\ &=0 \end{align*} ∫t1t2sin(nωt)cos(mωt) dt=∫t1t221(sin(n+m)ωt+sin(n−m)ωt) dt=21∫t1t2sin(n′ωt)+sin(m′ωt) dt=21(∫t1t2sin(n′ωt) dt+∫t1t2sin(m′ωt) dt)=0
-
-
也就是说三角函数系有正交性,也就是一个在 [ t 1 , t 2 ] [t_1,t_2] [t1,t2] 有定义的 f ( t ) f(t) f(t),可以表示为
f ( t ) = a 0 + a 1 cos ( ω t ) + b 1 sin ( ω t ) + ⋯ + a n cos ( n ω t ) + b n sin ( n ω t ) + ⋯ = a 0 + ∑ n = 1 ∞ ( a n cos ( n ω t ) + b n sin ( n ω t ) ) \begin{align*} f(t)&=a_0+a_1\cos (\omega t)+b_1\sin(\omega t)+\cdots+a_n\cos (n \omega t)+b_n\sin (n\omega t)+\cdots \\ &=a_0+\sum_{n=1}^{\infty}(a_n\cos (n\omega t)+b_n\sin (n\omega t)) \end{align*} f(t)=a0+a1cos(ωt)+b1sin(ωt)+⋯+ancos(nωt)+bnsin(nωt)+⋯=a0+n=1∑∞(ancos(nωt)+bnsin(nωt))
2.2.2 三角函数系的系数
如何求得表示 f ( t ) f(t) f(t) 的三角函数系的系数?
-
那么接下来需要求得 f ( t ) f(t) f(t) 函数的系数。与上文的正交函数类似,与正交函数中的系数 a n a_n an 相比,此处有三处系数 a 0 , a n a_0,a_n a0,an 和 b n b_n bn (此时 n > 0 n>0 n>0)
-
首先求 a 0 a_0 a0 的值,对 t t t 求积分:
∫ t 1 t 2 f ( t ) d t = ∫ t 1 t 2 ( a 0 + ∑ n = 1 ∞ ( a n cos ( n ω ) t + b n sin ( n ω t ) ) d t ) d t = ∫ t 1 t 2 a 0 d t + 0 = ( t 2 − t 1 ) a 0 a 0 = 1 t 2 − t 1 ∫ t 1 t 2 f ( t ) d t = 1 t 2 − t 1 ∫ t 1 t 2 f ( t ) ⋅ cos ( 0 ω t ) d t \begin{align*} \int_{t_1}^{t_2}f(t)\text{ d}t&=\int_{t_1}^{t_2}\left (a_0+\sum_{n=1}^{\infty}(a_n\cos (n\omega )t+b_n\sin (n\omega t))\text{ d}t\right )\text{ d}t\\ &=\int_{t_1}^{t_2}a_0\text{ d}t+0\\ &=(t_2-t_1)a_0\\ a_0 &=\frac{1}{t_2-t_1}\int_{t_1}^{t_2}f(t)\text{ d}t\\ &=\frac{1}{t_2-t_1}\int_{t_1}^{t_2}f(t)\cdot \cos (0\omega t) \text{ d}t \end{align*} ∫t1t2f(t) dta0=∫t1t2(a0+n=1∑∞(ancos(nω)t+bnsin(nωt)) dt) dt=∫t1t2a0 dt+0=(t2−t1)a0=t2−t11∫t1t2f(t) dt=t2−t11∫t1t2f(t)⋅cos(0ωt) dt -
为了求系数 a n / b n a_n/b_n an/bn,为等式两边乘上 a n / b n a_n/b_n an/bn 的对应项 cos n ω t / sin n ω t \cos n\omega t/\sin n\omega t cosnωt/sinnωt 再求积分,去掉值为0的正交项,只留下 m = n m=n m=n 时的 cos / sin ) \cos/\sin) cos/sin) 项。为区分符号设定此时 ω = 2 π t 2 − t 1 \omega=\frac{2\pi}{t_2-t_1} ω=t2−t12π:
∫ t 1 t 2 f ( t ) ⋅ cos ( m ω t ) d t = a 0 ∫ t 1 t 2 cos ( m ω t ) d t + ∑ n = 1 ∞ ( a n ∫ t 1 t 2 cos ( m ω t ) ⋅ cos ( n ω t ) d t + b n ∫ t 1 t 2 cos ( m ω t ) ⋅ sin ( n ω t ) d t ) = 0 + a n ∫ t 1 t 2 cos 2 ( n ω t ) d t + 0 \begin{align*} \int_{t_1}^{t_2}f(t)\cdot \cos (m\omega t) \text{ d}t&=a_0\int_{t_1}^{t_2} \cos (m\omega t) \text{ d}t + \sum_{n=1}^{\infty}\left(a_n\int_{t_1}^{t_2} \cos (m\omega t)\cdot \cos (n\omega t)\text{ d} t+b_n \int_{t_1}^{t_2} \cos (m\omega t)\cdot\sin (n\omega t)\text{ d}t\right )\\ &= 0 + a_n \int_{t_1}^{t_2} \cos^2 (n\omega t)\text{ d}t + 0 \end{align*} ∫t1t2f(t)⋅cos(mωt) dt=a0∫t1t2cos(mωt) dt+n=1∑∞(an∫t1t2cos(mωt)⋅cos(nωt) dt+bn∫t1t2cos(mωt)⋅sin(nωt) dt)=0+an∫t1t2cos2(nωt) dt+0
利用倍角公式 cos 2 α = 2 cos 2 α − 1 \cos 2\alpha=2\cos^2\alpha-1 cos2α=2cos2α−1,得到:
∫ t 1 t 2 f ( t ) ⋅ cos ( n ω t ) d t = a n ∫ t 1 t 2 cos 2 ( n ω t ) d t = a n 2 ∫ t 1 t 2 ( 1 + cos ( 2 n ω t ) ) d t = a n 2 ( ∫ t 1 t 2 1 d t + ∫ t 1 t 2 cos ( n ′ ω t ) d t ) = a n ( t 2 − t 1 ) 2 a n = 2 t 2 − t 1 ∫ t 1 t 2 f ( t ) ⋅ cos ( n ω t ) d t \begin{align*} \int_{t_1}^{t_2}f(t)\cdot \cos (n\omega t) \text{ d}t &= a_n \int_{t_1}^{t_2} \cos^2 (n\omega t)\text{ d}t\\ &=\frac{a_n}{2}\int_{t_1}^{t_2}(1+\cos (2n\omega t))\text{ d}t\\ &=\frac{a_n}{2}\left(\int_{t_1}^{t_2}1\text{ d}t+\int_{t_1}^{t_2}\cos (n'\omega t) \text{ d}t\right)\\ &=\frac{a_n(t_2-t_1)}{2}\\ a_n&=\frac{2}{t_2-t_1}\int_{t_1}^{t_2}f(t)\cdot \cos (n\omega t) \text{ d}t \end{align*} ∫t1t2f(t)⋅cos(nωt) dtan=an∫t1t2cos2(nωt) dt=2an∫t1t2(1+cos(2nωt)) dt=2an(∫t1t21 dt+∫t1t2cos(n′ωt) dt)=2an(t2−t1)=t2−t12∫t1t2f(t)⋅cos(nωt) dt -
同理,利用倍角公式 cos 2 α = 1 − 2 sin 2 α \cos 2\alpha = 1-2\sin^2\alpha cos2α=1−2sin2α,可得
∫ t 1 t 2 f ( t ) ⋅ sin ( m ω t ) d t = a 0 ∫ t 1 t 2 sin ( m ω t ) d t + ∑ n = 1 ∞ ( a n ∫ t 1 t 2 sin ( m ω t ) ⋅ cos ( n ω t ) d t + b n ∫ t 1 t 2 sin ( m ω t ) ⋅ sin ( n ω t ) d t ) = 0 + b n ∫ t 1 t 2 sin 2 ( n ω t ) d t + 0 = b n 2 ∫ t 1 t 2 ( 1 − cos ( 2 n ω t ) ) d t = b n 2 ( ∫ t 1 t 2 1 d t − ∫ t 1 t 2 cos ( n ′ ω t ) d t ) = b n ( t 2 − t 1 ) 2 b n = 2 t 2 − t 1 ∫ t 1 t 2 f ( t ) ⋅ sin ( n ω t ) d t \begin{align*} \int_{t_1}^{t_2}f(t)\cdot \sin (m\omega t) \text{ d}t&=a_0\int_{t_1}^{t_2} \sin (m\omega t) \text{ d}t + \sum_{n=1}^{\infty}\left(a_n\int_{t_1}^{t_2} \sin (m\omega t)\cdot \cos (n\omega t)\text{ d} t+b_n \int_{t_1}^{t_2} \sin (m\omega t)\cdot\sin (n\omega t)\text{ d}t\right )\\ &= 0 + b_n \int_{t_1}^{t_2} \sin^2 (n\omega t)\text{ d}t + 0\\ &=\frac{b_n}{2}\int_{t_1}^{t_2}(1-\cos (2n\omega t))\text{ d}t\\ &=\frac{b_n}{2}\left(\int_{t_1}^{t_2}1\text{ d}t-\int_{t_1}^{t_2}\cos (n'\omega t) \text{ d}t\right)\\ &=\frac{b_n(t_2-t_1)}{2}\\ b_n&=\frac{2}{t_2-t_1}\int_{t_1}^{t_2}f(t)\cdot \sin (n\omega t) \text{ d}t \end{align*} ∫t1t2f(t)⋅sin(mωt) dtbn=a0∫t1t2sin(mωt) dt+n=1∑∞(an∫t1t2sin(mωt)⋅cos(nωt) dt+bn∫t1t2sin(mωt)⋅sin(nωt) dt)=0+bn∫t1t2sin2(nωt) dt+0=2bn∫t1t2(1−cos(2nωt)) dt=2bn(∫t1t21 dt−∫t1t2cos(n′ωt) dt)=2bn(t2−t1)=t2−t12∫t1t2f(t)⋅sin(nωt) dt
对比 a 0 , a n a_0,a_n a0,an 和 b n b_n bn ,为了能使 n n n 也能表示 n = 0 n=0 n=0 的情况,令 a 0 = 2 a 0 a_0=2a_0 a0=2a0。此时我们可以得到
f ( t ) = a 0 2 + ∑ n = 1 ∞ ( a n cos ( n ω t ) + b n sin ( n ω t ) ) a 0 = 2 t 2 − t 1 ∫ t 1 t 2 f ( t ) d t a n = 2 t 2 − t 1 ∫ t 1 t 2 f ( t ) ⋅ cos ( n ω t ) d t b n = 2 t 2 − t 1 ∫ t 1 t 2 f ( t ) ⋅ sin ( n ω t ) d t \begin{align*} f(t)&=\frac{a_0}{2}+\sum_{n=1}^{\infty}\left (a_n\cos(n\omega t)+b_n \sin(n\omega t)\right )\\ a_0&=\frac{2}{t_2-t_1}\int_{t_1}^{t_2}f(t) \text{ d}t\\ a_n&=\frac{2}{t_2-t_1}\int_{t_1}^{t_2}f(t)\cdot \cos (n\omega t) \text{ d}t \\ b_n&=\frac{2}{t_2-t_1}\int_{t_1}^{t_2}f(t)\cdot \sin (n\omega t) \text{ d}t \end{align*} f(t)a0anbn=2a0+n=1∑∞(ancos(nωt)+bnsin(nωt))=t2−t12∫t1t2f(t) dt=t2−t12∫t1t2f(t)⋅cos(nωt) dt=t2−t12∫t1t2f(t)⋅sin(nωt) dt
-
至此傅里叶级数可以将任意一个周期函数 f ( t ) f(t) f(t) 分解为多个三角函数的组合,从而完成时域到频域的转换。而傅里叶级数是处理周期函数的,为了处理非周期的普通函数,需要把周期 T T T 从 2 π 2\pi 2π 趋向于无穷,也就是傅里叶变换。
2.3 复指数函数系表示 f ( t ) f(t) f(t)
2.3.1 复指数函数系的系数
在傅里叶变换之前,我们使用一个更加简单直观的表示,将傅里叶的三角函数形式转化为傅里叶的复指数形式。由欧拉公式 e i θ = cos ( θ ) + i sin ( θ ) e^{i\theta}=\cos(\theta)+i\sin(\theta) eiθ=cos(θ)+isin(θ) 可得:
cos ( n ω t ) = 1 2 ( e i n ω t + e − i n ω t ) sin ( n ω t ) = 1 2 i ( e i n ω t − e − i n ω t ) = − i 2 ( e i n ω t − e − i n ω t ) \begin{align*} \cos(n\omega t)&=\frac{1}{2}(e^{in\omega t}+e^{-in\omega t})\\ \sin(n\omega t)&=\frac{1}{2i}(e^{in\omega t}-e^{-in\omega t})=-\frac{i}{2}(e^{in\omega t}-e^{-in\omega t}) \end{align*} cos(nωt)sin(nωt)=21(einωt+e−inωt)=2i1(einωt−e−inωt)=−2i(einωt−e−inωt)
代入 f ( x ) f(x) f(x):
f ( t ) = a 0 2 + ∑ n = 1 ∞ ( a n 2 ( e i n ω t + e − i n ω t ) − i b n 2 ( e i n ω t − e − i n ω t ) ) = a 0 2 + ∑ n = 1 ∞ ( a n − i b n 2 e i n ω t + a n + i b n 2 e − i n ω t ) \begin{align*} f(t)&=\frac{a_0}{2}+\sum_{n=1}^{\infty}\left (\frac{a_n}{2}(e^{in\omega t}+e^{-in\omega t})-\frac{ib_n}{2} (e^{in\omega t}-e^{-in\omega t})\right )\\ &=\frac{a_0}{2}+\sum_{n=1}^\infty \left(\frac{a_n-ib_n}{2}e^{in\omega t} +\frac{a_n+ib_n}{2}e^{-in\omega t}\right) \end{align*} f(t)=2a0+n=1∑∞(2an(einωt+e−inωt)−2ibn(einωt−e−inωt))=2a0+n=1∑∞(2an−ibneinωt+2an+ibne−inωt)
重新求系数:
a n − i b n 2 = 1 t 2 − t 1 ( ∫ t 1 t 2 f ( t ) ⋅ cos ( n ω t ) d t − i ⋅ ∫ t 1 t 2 f ( t ) ⋅ sin ( n ω t ) d t ) = 1 t 2 − t 1 ∫ t 1 t 2 f ( t ) ⋅ ( cos ( n ω t ) − i ⋅ sin ( n ω t ) ) d t = 1 t 2 − t 1 ∫ t 1 t 2 f ( t ) ⋅ ( 1 2 ( e i n ω t + e − i n ω t ) − i ⋅ 1 2 i ( e i n ω t − e − i n ω t ) ) d t = 1 t 2 − t 1 ∫ t 1 t 2 f ( t ) ⋅ e − i n ω t d t a n + i b n 2 = 1 t 2 − t 1 ∫ t 1 t 2 f ( t ) ⋅ e i n ω t d t \begin{align*} \frac{a_n-ib_n}{2}&=\frac{1}{t_2-t_1}\left (\int_{t_1}^{t_2}f(t)\cdot \cos (n\omega t) \text{ d}t-i\cdot \int_{t_1}^{t_2}f(t)\cdot \sin (n\omega t) \text{ d}t\right )\\ &=\frac{1}{t_2-t_1}\int_{t_1}^{t_2}f(t)\cdot(\cos (n\omega t)-i\cdot\sin(n\omega t))\text{ d}t\\ &=\frac{1}{t_2-t_1}\int_{t_1}^{t_2}f(t)\cdot\left (\frac{1}{2}(e^{in\omega t}+e^{-in\omega t})-i\cdot\frac{1}{2i}(e^{in\omega t}-e^{-in\omega t})\right)\text{ d}t\\ &=\frac{1}{t_2-t_1}\int_{t_1}^{t_2}f(t)\cdot e^{-in\omega t}\text{ d}t\\ \frac{a_n+ib_n}{2}&=\frac{1}{t_2-t_1}\int_{t_1}^{t_2}f(t)\cdot e^{in\omega t}\text{ d}t \end{align*} 2an−ibn2an+ibn=t2−t11(∫t1t2f(t)⋅cos(nωt) dt−i⋅∫t1t2f(t)⋅sin(nωt) dt)=t2−t11∫t1t2f(t)⋅(cos(nωt)−i⋅sin(nωt)) dt=t2−t11∫t1t2f(t)⋅(21(einωt+e−inωt)−i⋅2i1(einωt−e−inωt)) dt=t2−t11∫t1t2f(t)⋅e−inωt dt=t2−t11∫t1t2f(t)⋅einωt dt
代入 f ( t ) f(t) f(t) ,为了区分,将原系数 a 0 , a n a_0,a_n a0,an 和 b n b_n bn 中的 t t t 表示为 τ \tau τ 。可得:
f ( t ) = a 0 2 + ∑ n = 1 ∞ ( ( 1 t 2 − t 1 ∫ t 1 t 2 f ( τ ) ⋅ e − i n ω τ d τ ) e i n ω t + ( 1 t 2 − t 1 ∫ t 1 t 2 f ( τ ) ⋅ e i n ω τ d τ ) e − i n ω t ) = a 0 2 + 1 t 2 − t 1 ∑ n = 1 ∞ ( ∫ t 1 t 2 f ( τ ) ⋅ e − i n ω τ d τ ) e i n ω t + 1 t 2 − t 1 ∑ n = 1 ∞ ( ∫ t 1 t 2 f ( τ ) ⋅ e i n ω τ d τ ) e − i n ω t = 1 t 2 − t 1 ∫ t 1 t 2 f ( τ ) d τ + 1 t 2 − t 1 ∑ n = 1 ∞ ( ∫ t 1 t 2 f ( τ ) ⋅ e − i n ω τ d τ ) e i n ω t + 1 t 2 − t 1 ∑ n = − ∞ − 1 ( ∫ t 1 t 2 f ( τ ) ⋅ e − i n ω τ d τ ) e i n ω t = 1 t 2 − t 1 ∑ n = − ∞ ∞ ( ∫ t 1 t 2 f ( τ ) ⋅ e − i n ω τ d τ ) e i n ω t = ∑ n = − ∞ ∞ c n e i n ω t c n = 1 t 2 − t 1 ∫ t 1 t 2 f ( τ ) ⋅ e − i n ω τ d τ \begin{align*} f(t)&=\frac{a_0}{2}+\sum_{n=1}^\infty \left(\left(\frac{1}{t_2-t_1}\int_{t_1}^{t_2}f(\tau)\cdot e^{-in\omega \tau}\text{ d}\tau\right)e^{in\omega t} +\left(\frac{1}{t_2-t_1}\int_{t_1}^{t_2}f(\tau)\cdot e^{in\omega \tau}\text{ d}\tau\right)e^{-in\omega t}\right)\\ &=\frac{a_0}{2}+\frac{1}{t_2-t_1}\sum_{n=1}^\infty \left(\int_{t_1}^{t_2}f(\tau)\cdot e^{-in\omega \tau}\text{ d}\tau \right)e^{in\omega t}+\frac{1}{t_2-t_1}\sum_{n=1}^\infty \left(\int_{t_1}^{t_2}f(\tau)\cdot e^{in\omega \tau}\text{ d}\tau \right)e^{-in\omega t}\\ &=\frac{1}{t_2-t_1}\int_{t_1}^{t_2}f(\tau) \text{ d}\tau+\frac{1}{t_2-t_1}\sum_{n=1}^\infty \left(\int_{t_1}^{t_2}f(\tau)\cdot e^{-in\omega \tau}\text{ d}\tau \right)e^{in\omega t}+\frac{1}{t_2-t_1}\sum_{n=-\infty}^{-1} \left(\int_{t_1}^{t_2}f(\tau)\cdot e^{-in\omega \tau}\text{ d}\tau \right)e^{in\omega t}\\ &=\frac{1}{t_2-t_1}\sum_{n=-\infty}^\infty \left(\int_{t_1}^{t_2}f(\tau)\cdot e^{-in\omega \tau}\text{ d}\tau \right)e^{in\omega t}\\ &=\sum_{n=-\infty}^{\infty}c_ne^{in\omega t}\\ c_n&=\frac{1}{t_2-t_1}\int_{t_1}^{t_2}f(\tau)\cdot e^{-in\omega \tau}\text{ d}\tau \end{align*} f(t)cn=2a0+n=1∑∞((t2−t11∫t1t2f(τ)⋅e−inωτ dτ)einωt+(t2−t11∫t1t2f(τ)⋅einωτ dτ)e−inωt)=2a0+t2−t11n=1∑∞(∫t1t2f(τ)⋅e−inωτ dτ)einωt+t2−t11n=1∑∞(∫t1t2f(τ)⋅einωτ dτ)e−inωt=t2−t11∫t1t2f(τ) dτ+t2−t11n=1∑∞(∫t1t2f(τ)⋅e−inωτ dτ)einωt+t2−t11n=−∞∑−1(∫t1t2f(τ)⋅e−inωτ dτ)einωt=t2−t11n=−∞∑∞(∫t1t2f(τ)⋅e−inωτ dτ)einωt=n=−∞∑∞cneinωt=t2−t11∫t1t2f(τ)⋅e−inωτ dτ
也就是将 f ( t ) f(t) f(t) 看作基向量 e i n ω t e^{in\omega t} einωt 的线性组合。同样,此时傅里叶级数可以将任意一个周期函数 f ( x ) f(x) f(x) 分解为多个复指数形式的组合,从而完成时域到频域的转换。
2.3.2 复指数函数系的正交性
证明 e i n ω t e^{in\omega t} einωt 确实可以作为基向量,即证明复指数函数系的正交性,即证明对于 n ≠ m n\ne m n=m ,相对应的复指数内积 ⟨ e i n ω t , e i m ω t ⟩ = 0 \left \langle e^{in\omega t},e^{im\omega t} \right \rangle=0 ⟨einωt,eimωt⟩=0。注意两个复函数内积时要对一个求共轭,即 ⟨ f , g ⟩ : = ∫ a b f ( t ) g ( t ) ‾ d t \left \langle f,g\right \rangle:=\int_a^b f(t)\overline{g(t)}\text{ d}t ⟨f,g⟩:=∫abf(t)g(t) dt
⟨ e i n ω t , e i m ω t ⟩ = ∫ t 1 t 2 e i n ω t ⋅ e − i m ω t d t = ∫ t 1 t 2 e i ω t ( n − m ) d t = 1 i ω ( n − m ) e i ω t ( n − m ) ∣ t 1 t 2 = 1 i ω ( n − m ) ( e i ω ( n − m ) t 2 − e i ω ( n − m ) t 1 ) \begin{align*} \left \langle e^{in\omega t},e^{im\omega t} \right \rangle&=\int_{t_1}^{t_2} e^{in\omega t}\cdot e^{-im\omega t} \text{ d}t\\ &=\int_{t_1}^{t_2} e^{i\omega t(n-m)} \text{ d}t\\ &=\frac{1}{i\omega(n-m)}e^{i\omega t(n-m)}\bigg|_{t_1}^{t_2}\\ &=\frac{1}{i\omega(n-m)}\left (e^{i\omega (n-m)t_2}-e^{i\omega (n-m)t_1}\right) \end{align*} ⟨einωt,eimωt⟩=∫t1t2einωt⋅e−imωt dt=∫t1t2eiωt(n−m) dt=iω(n−m)1eiωt(n−m) t1t2=iω(n−m)1(eiω(n−m)t2−eiω(n−m)t1)
由于 f cplx n ( t ) = e i n ω t f^{n}_{\text{cplx}}(t)=e^{in\omega t} fcplxn(t)=einωt 的周期 T n = 2 π n ω = t 2 − t 1 n T_n=\frac{2\pi}{n\omega}=\frac{t_2-t_1}{n} Tn=nω2π=nt2−t1 ,可以得出 t 2 − t 1 = n T n t_2-t_1=nT_n t2−t1=nTn,即区间 [ t 1 , t 2 ] [t_1,t_2] [t1,t2] 是 f cplx n ( t ) f^{n}_{\text{cplx}}(t) fcplxn(t) 的周期的整数倍,即 [ t 2 , t 1 ] [t_2,t_1] [t2,t1] 一定是 f cplx n ( t ) f^{n}_{\text{cplx}}(t) fcplxn(t) 的一个周期,即 f cplx n ( t 1 ) = f cplx n ( t 2 ) f^{n}_{\text{cplx}}(t_1)=f^{n}_{\text{cplx}}(t_2) fcplxn(t1)=fcplxn(t2),那么当 n = n − m = n ′ n=n-m=n' n=n−m=n′ 时:
⟨ e i n ω t , e i m ω t ⟩ = 1 i ω ( n − m ) ( e i ω n ′ t 2 − e i ω n ′ t 1 ) = 1 i ω ( n − m ) ( f cplx n ′ ( t 2 ) − f cplx n ′ ( t 1 ) ) = 1 i ω ( n − m ) ⋅ 0 = 0 \begin{align*} \left \langle e^{in\omega t},e^{im\omega t} \right \rangle&=\frac{1}{i\omega(n-m)}\left (e^{i\omega n't_2}-e^{i\omega n't_1}\right)\\ &=\frac{1}{i\omega(n-m)}\left (f^{n'}_{\text{cplx}}(t_2)-f^{n'}_{\text{cplx}}(t_1)\right)\\ &=\frac{1}{i\omega(n-m)}\cdot 0\\ &=0 \end{align*} ⟨einωt,eimωt⟩=iω(n−m)1(eiωn′t2−eiωn′t1)=iω(n−m)1(fcplxn′(t2)−fcplxn′(t1))=iω(n−m)1⋅0=0
2.4 傅里叶级数总结
至此我们得到了周期性信号 f ( t ) f(t) f(t) 的三角函数系表示:
f ( t ) = a 0 2 + ∑ n = 1 ∞ ( a n cos ( n ω t ) + b n sin ( n ω t ) ) a 0 = 2 t 2 − t 1 ∫ t 1 t 2 f ( t ) d t a n = 2 t 2 − t 1 ∫ t 1 t 2 f ( t ) ⋅ cos ( n ω t ) d t b n = 2 t 2 − t 1 ∫ t 1 t 2 f ( t ) ⋅ sin ( n ω t ) d t \begin{align*} f(t)&=\frac{a_0}{2}+\sum_{n=1}^{\infty}\left (a_n\cos(n\omega t)+b_n \sin(n\omega t)\right )\\ a_0&=\frac{2}{t_2-t_1}\int_{t_1}^{t_2}f(t) \text{ d}t\\ a_n&=\frac{2}{t_2-t_1}\int_{t_1}^{t_2}f(t)\cdot \cos (n\omega t) \text{ d}t \\ b_n&=\frac{2}{t_2-t_1}\int_{t_1}^{t_2}f(t)\cdot \sin (n\omega t) \text{ d}t \end{align*} f(t)a0anbn=2a0+n=1∑∞(ancos(nωt)+bnsin(nωt))=t2−t12∫t1t2f(t) dt=t2−t12∫t1t2f(t)⋅cos(nωt) dt=t2−t12∫t1t2f(t)⋅sin(nωt) dt
和复指数函数系表示:
f ( t ) = ∑ n = − ∞ ∞ c n e i n ω t c n = 1 t 2 − t 1 ∫ t 1 t 2 f ( τ ) ⋅ e − i n ω τ d τ \begin{align*} f(t) &=\sum_{n=-\infty}^{\infty}c_ne^{in\omega t}\\ c_n&=\frac{1}{t_2-t_1}\int_{t_1}^{t_2}f(\tau)\cdot e^{-in\omega \tau}\text{ d}\tau \end{align*} f(t)cn=n=−∞∑∞cneinωt=t2−t11∫t1t2f(τ)⋅e−inωτ dτ
其中 t 2 − t 1 t_2-t_1 t2−t1 是 f ( t ) f(t) f(t) 的一个周期, ω = 2 π t 2 − t 1 \omega=\frac{2\pi}{t_2-t_1} ω=t2−t12π。
3 傅里叶变换
此时的傅里叶级数只是针对周期性函数的,即转换为频域时,频率的个数是有限多个,即频域图是离散的。傅里叶变换就是将傅里叶级数推广到一般的非周期性函数。
接下来对复指数形式的傅里叶级数进行一个从离散到连续的过程,即将傅里叶级数扩展到非周期性函数(周期无限大的函数)中。这里要用到黎曼积分的定义。此时 ω = 2 π t 2 − t 1 \omega=\frac{2\pi}{t_2-t_1} ω=t2−t12π, 当周期 t 2 − t 1 → ∞ t_2-t_1\to\infty t2−t1→∞ 时, ω → 0 \omega \to 0 ω→0。此时我们令:
ω n = n ω = 2 π n t 2 − t 1 F ( ω ) = ∫ t 1 t 2 f ( τ ) ⋅ e − i ω τ d τ \begin{align*} \omega_n&=n\omega=\frac{2\pi n}{t_2-t_1}\\ F(\omega)&=\int_{t_1}^{t_2}f(\tau)\cdot e^{-i\omega \tau}\text{ d}\tau \end{align*} ωnF(ω)=nω=t2−t12πn=∫t1t2f(τ)⋅e−iωτ dτ
那么 f ( t ) f(t) f(t) 可以写成:
f ( t ) = ∑ n = − ∞ ∞ 1 t 2 − t 1 F ( ω n ) e i ω n t \begin{align*} f(t)=\sum_{n=-\infty}^{\infty}\frac{1}{t_2-t_1}F(\omega_n)e^{i\omega_n t} \end{align*} f(t)=n=−∞∑∞t2−t11F(ωn)eiωnt
根据积分的黎曼和表达式 :
∫ a b f riman ( x ) d x = lim λ → 0 ∑ n = 0 ∞ f riman ( x n ) ⋅ λ \int_a^bf_{\text{riman}}(x)\text{ d}x = \underset{\lambda\to 0}{\lim}\sum_{n=0}^{\infty}f_{\text{riman}}(x_n)\cdot \lambda ∫abfriman(x) dx=λ→0limn=0∑∞friman(xn)⋅λ
则对于 f ( t ) f(t) f(t) 来说:
f riman ( ω ) = F ( ω ) e i ω t λ = Δ ω = ω n − ω n − 1 = 2 π n t 2 − t 1 − 2 π ( n − 1 ) t 2 − t 1 = 2 π t 2 − t 1 \begin{align*} f_{\text{riman}}(\omega)&=F(\omega)e^{i\omega t}\\ \lambda & = \Delta \omega= \omega_n-\omega_{n-1}=\frac{2\pi n}{t_2-t_1} - \frac{2\pi (n-1)}{t_2-t_1}=\frac{2\pi}{t_2-t_1} \end{align*} friman(ω)λ=F(ω)eiωt=Δω=ωn−ωn−1=t2−t12πn−t2−t12π(n−1)=t2−t12π
因此可以将 f ( t ) f(t) f(t) 写成
f ( t ) = 1 2 π ∑ n = − ∞ ∞ 2 π t 2 − t 1 F ( ω n ) e i ω n t = 1 2 π ∑ n = − ∞ ∞ λ ⋅ f riman ( ω n ) = 1 2 π ∫ − ∞ ∞ f riman ( ω ) d ω = 1 2 π ∫ − ∞ ∞ F ( ω ) e i ω t d ω \begin{align*} f(t)&=\frac{1}{2\pi}\sum_{n=-\infty}^{\infty}\frac{2\pi}{t_2-t_1}F(\omega_n)e^{i\omega_n t}\\ &= \frac{1}{2\pi}\sum_{n=-\infty}^{\infty}\lambda \cdot f_{\text{riman}}(\omega_n)\\ &=\frac{1}{2\pi}\int_{-\infty}^{\infty} f_{\text{riman}}(\omega) \text{ d} \omega\\ &=\frac{1}{2\pi}\int_{-\infty}^{\infty} F(\omega)e^{i\omega t} \text{ d} \omega \end{align*} f(t)=2π1n=−∞∑∞t2−t12πF(ωn)eiωnt=2π1n=−∞∑∞λ⋅friman(ωn)=2π1∫−∞∞friman(ω) dω=2π1∫−∞∞F(ω)eiωt dω
此时周期 t 2 − t 1 → ∞ t_2-t_1\to\infty t2−t1→∞,这就是傅里叶变换:
F ( ω ) = ∫ − ∞ ∞ f ( t ) ⋅ e − i ω t d t F(\omega)=\int_{-\infty}^{\infty}f(t)\cdot e^{-i\omega t}\text{ d}t F(ω)=∫−∞∞f(t)⋅e−iωt dt
和傅里叶逆变换:
f ( t ) = 1 2 π ∫ − ∞ ∞ F ( ω ) e i ω t d ω f(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty} F(\omega)e^{i\omega t} \text{ d} \omega f(t)=2π1∫−∞∞F(ω)eiωt dω
参考资料:
深入理解正交函数 https://zhuanlan.zhihu.com/p/338045910
傅里叶分析之掐死教程 https://zhuanlan.zhihu.com/p/19763358
三角函数和 e i k x e^{ikx} eikx的正交性 https://zhuanlan.zhihu.com/p/597931378
如何理解傅里叶变换公式?https://www.zhihu.com/question/19714540/answer/1119070975
傅里叶变换 https://zhuanlan.zhihu.com/p/104079068
浅谈傅里叶变换:关于傅里叶变换的几种几何学解释 https://mp.weixin.qq.com/s/rkDrHrTJwAbGL0znvnk_pA
傅里叶系列(二)傅里叶变换的推导 https://zhuanlan.zhihu.com/p/41875010
相关文章:

从零开始傅里叶变换
从零开始傅里叶变换 1 Overview2 傅里叶级数2.1 基向量2.2 三角函数系表示 f ( t ) f(t) f(t)2.2.1 三角函数系的正交性2.2.2 三角函数系的系数 2.3 复指数函数系表示 f ( t ) f(t) f(t)2.3.1 复指数函数系的系数2.3.2 复指数函数系的正交性 2.4 傅里叶级数总结 3 傅里叶变换…...

解决1万条数据前端渲染不卡的问题
万级数据前端渲染优化 解决思路requestAnimationFrame完整代码 解决思路 将数据分组,通过定时器或requestAnimationFrame两种方式分组渲染到Dom上 requestAnimationFrame 渲染数据-动画requestAnimationFram方法 使用requestAnimationFrame可以将动画的每一帧绘制…...

如何编写一个API——Python代码示例及拓展
下面是一个必备的API的demo,包括用户认证、数据库交互、错误处理和更复杂的异步任务处理。使用Flask来创建一个RESTful API,涉及用户注册、登录、以及获取用户信息的功能。 示例1:编写API 安装依赖 首先,你需要安装以下库来支持示例的功能: pip install flask flask-c…...
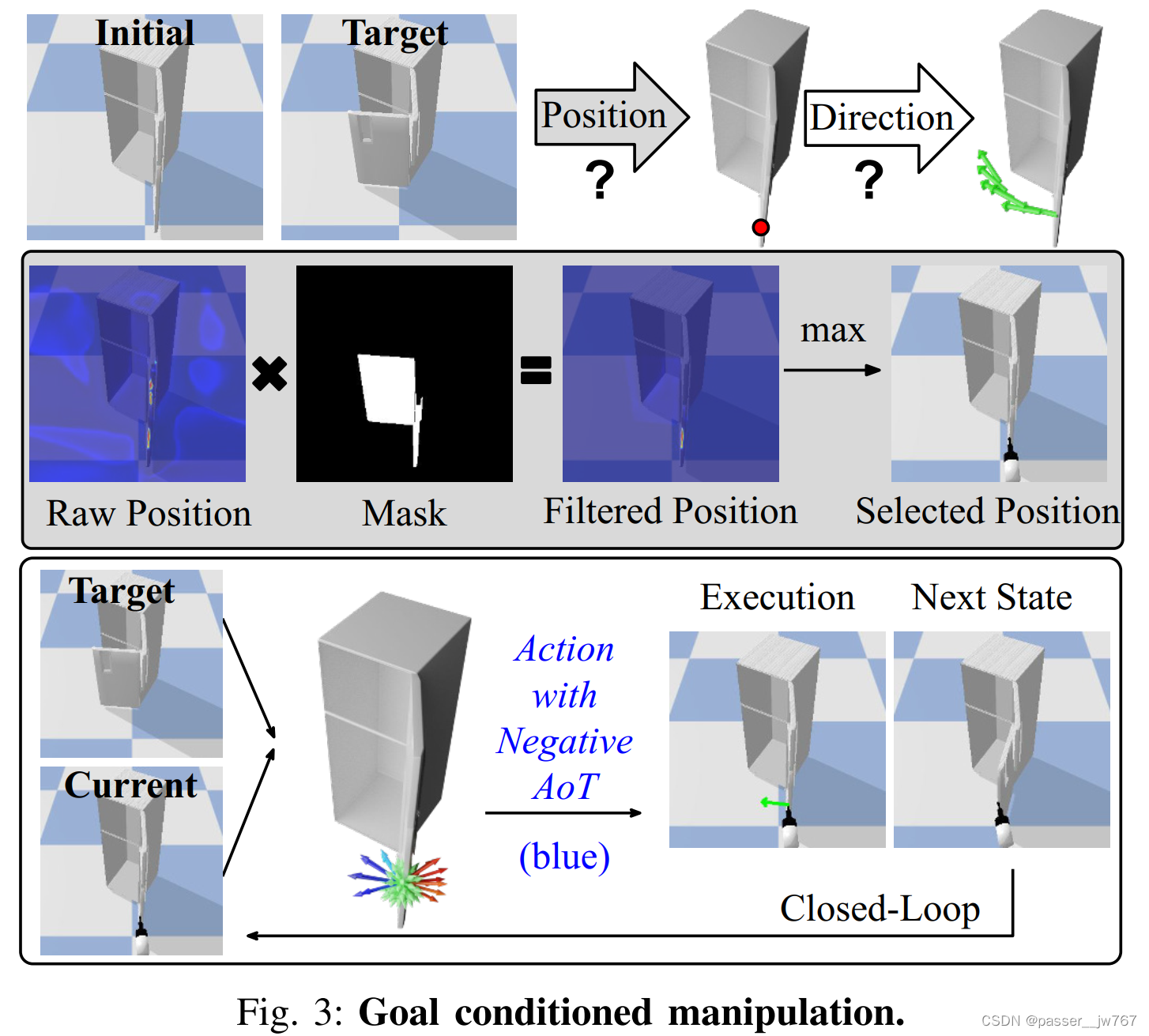
UMPNet: Universal Manipulation Policy Network for Articulated Objects
1. 摘要 UMPNet是一个基于图像的策略网络,能够推理用于操纵铰接物体的闭环动作序列。该策略支持6DoF动作表示和可变长度轨迹。 为处理多种类的物体,该策略从不同的铰接结构中学习,并泛化到未见过的物体或类别上。该策略是以自监督探索的方式…...

高通 Android 12/13冻结屏幕
冻结屏幕很多第一次听到以为是Android一种异常现象,实则不然,就是防止用户在做一些非法操作导致问题防止安全漏洞问题。 1、主要通过用户行为比如禁止下拉状态栏和按键以及onTouch事件拦截等,不知道请看这篇文章(Touch事件传递流…...

C++实现图的存储和遍历
前言 许多新手友友在初学算法和数据结构时,会被图论支配过。我这里整理了一下图论常见的存储和遍历方式,仅供参考。如有问题,欢迎大佬们批评指正。 存储我将提到四种方式:邻接矩阵、vector实现邻接表、数组模拟单链表实现的前向星…...
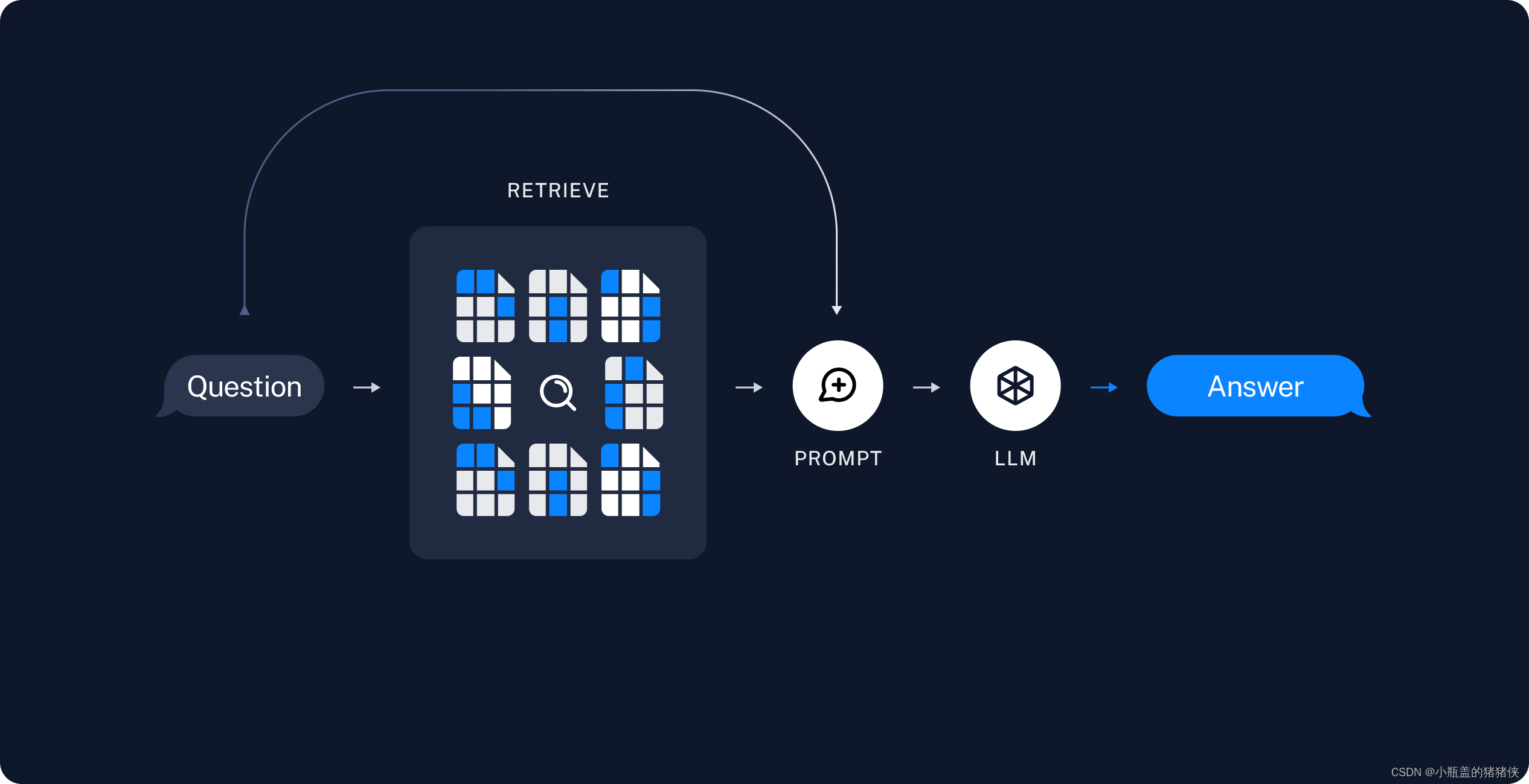
AI--构建检索增强生成 (RAG) 应用程序
LLM 所实现的最强大的应用之一是复杂的问答 (Q&A) 聊天机器人。这些应用程序可以回答有关特定源信息的问题。这些应用程序使用一种称为检索增强生成 (RAG) 的技术。 典型的 RAG 应用程序有两个主要组件 索引:从源中提取数据并对其进行索引的管道。这通常在线下…...
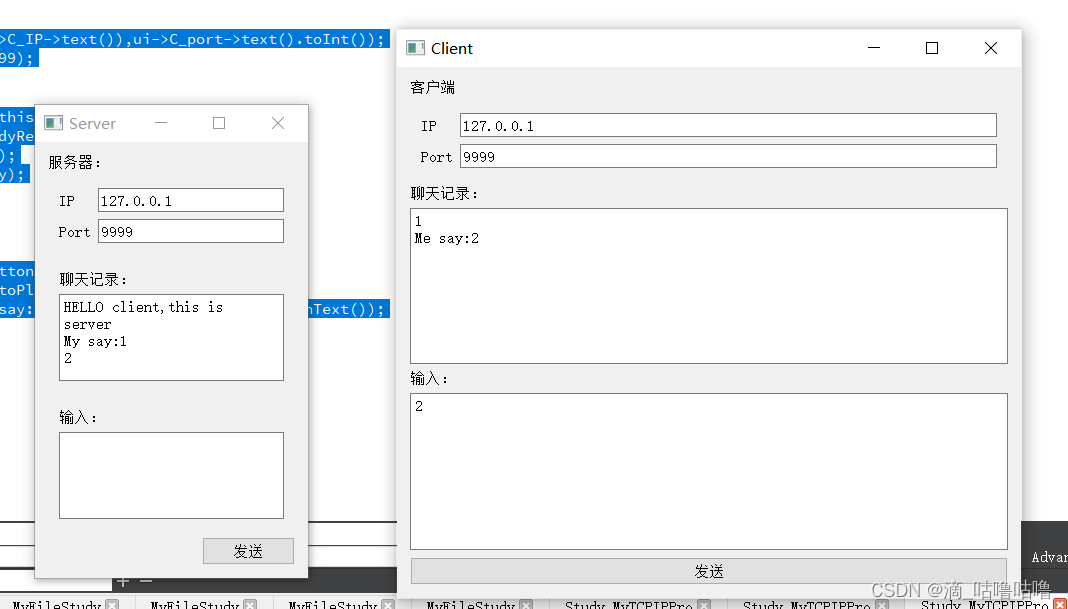
QT7_视频知识点笔记_4_文件操作,Socket通信:TCP/UDP
1.事件分发器,事件过滤器(重要程度:一般) event函数 2.文件操作(QFile) 实现功能:点击按钮,弹出对话框,并且用文件类读取出内容输出显示在控件上。 #include <QFi…...
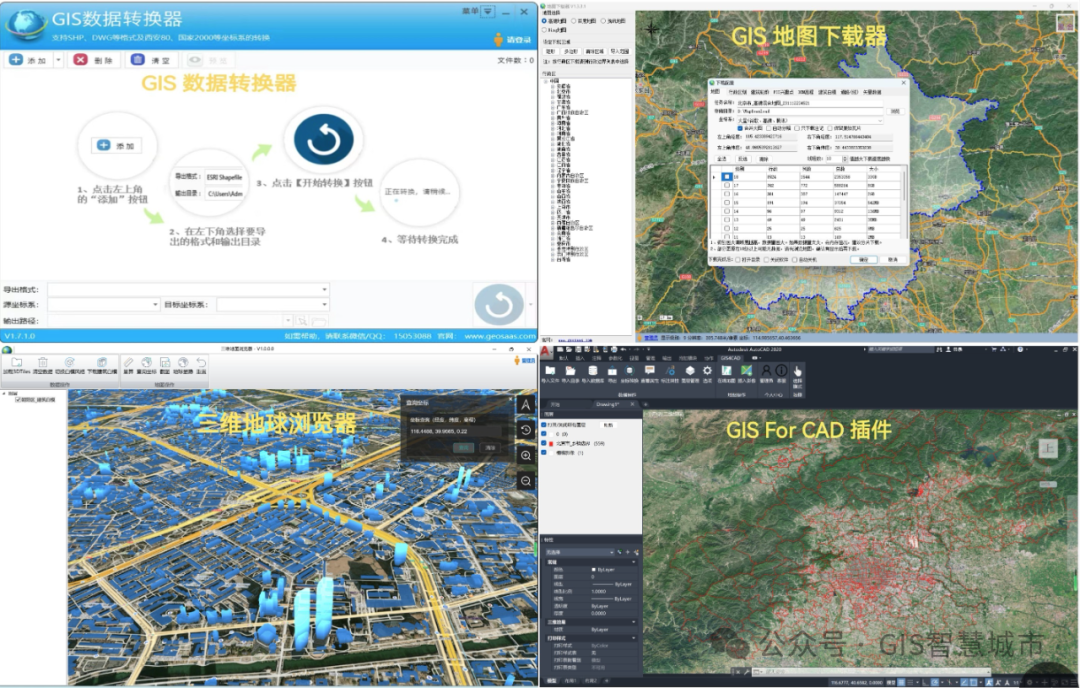
智慧社区管理系统:打造便捷、安全、和谐的新型社区生态
项目背景 在信息化、智能化浪潮席卷全球的今天,人们对于生活品质的需求日益提升,期待居住环境能与科技深度融合,实现高效、舒适、安全的生活体验。在此背景下,智慧社区管理系统应运而生,旨在借助现代信息技术手段&…...
CustomTkinter:便捷美化Tkinter的UI界面(附模板)
CustomTkinter是一个基于Tkinter的Python用户界面库。 pip3 install customtkinter它提供了各种UI界面常见的小部件。这些小部件可以像正常的Tkinter小部件一样创建和使用,也可以与正常的Tkinter元素一起使用。 它的优势如下: CustomTkinter的小部件和…...

使用MicroPython和pyboard开发板(15):使用LCD和触摸传感器
使用LCD和触摸传感器 pybaord的pyb对LCD设备也进行了封装,可以使用官方的LCD显示屏。将LCD屏连接到开发板,连接后。 使用LCD 先用REPL来做个实验,在MicroPython提示符中输入以下指令。请确保LCD面板连接到pyboard的方式正确。 >>…...

c++20 std::jthread 源码简单赏析与应用
std::jthread 说明: std::jthread 是 C20 中引入的一个新特性,它是线程库中的一个类,专门用于处理 std::thread 与 std::stop_token 和 std::stop_source 之间的交互,以支持更优雅和安全的线程停止机制。 std::stop_source控制…...

自动化测试里的数据驱动和关键字驱动思路的理解
🍅 视频学习:文末有免费的配套视频可观看 🍅 点击文末小卡片,免费获取软件测试全套资料,资料在手,涨薪更快 初次接触自动化测试时,对数据驱动和关键字驱动不甚理解,觉得有点故弄玄须…...

【30天精通Prometheus:一站式监控实战指南】第6天:mysqld_exporter从入门到实战:安装、配置详解与生产环境搭建指南,超详细
亲爱的读者们👋 欢迎加入【30天精通Prometheus】专栏!📚 在这里,我们将探索Prometheus的强大功能,并将其应用于实际监控中。这个专栏都将为你提供宝贵的实战经验。🚀 Prometheus是云原生和DevOps的…...
浅析智能体开发(第二部分):智能体设计模式和软件架构
大语言模型(LLM)驱动的智能体(AI Agent)展现出许多传统软件所不具备的特征。不仅与传统软件的设计理念、方法、工具和技术栈有显著的差异,AI原生(AI Native)的智能体还融入了多种新概念和技术。…...

Unity学习笔记---Transform组件
组件介绍 Transform组件在每个游戏对象中都存在,且只存在一个。该组件保存了游戏对象的位置、平移、旋转、缩放等信息。 组件相关方法 //获取当前游戏对象的Transform组件this.transform; getObject.transform; GetComponent<Transform>();//属性 gameObje…...
springboot+jsp校园理发店美容美发店信息管理系统0h29g
前台管理:会员管理、会员预定、开单点单、收银结帐、技师提成 后台管理:数据维护、物料管理、数据查询、报表分析、系统设置等 灵活的付款方式,支持现金、挂帐、会员卡,同时支持多种折扣方式并可按用户要求设置多种结帐类型善的充值卡管理模块:支持优惠卡…...

css - sass or scss ?
总的来说,Sass 和 SCSS 提供的功能是一样的,选择哪种语法主要取决于你的个人或团队的偏好。...

html5 笔记01
01 表单类型和属性 input的type属性 单行文本框: typetext 电子邮箱 : typeemail 地址路径 : type url 定义用于输入数字的字段: typenumber 手机号码: typetel 搜索框 : typesearch 定义颜色选择器 : typecolor 滑块控件 : typerange 定义日期 :typedate 定义输入时间的控件…...

E5063A是德科技e5063a网络分析仪
181-2461-8938产品概述: 简 述: E5063A 是低成本网络分析仪,可提供优化的性能和功能,适用于测试简单的无源器件,例如天线、电缆、滤波器和 PCB 等。它利用工业标准 ENA 系列始终如一的测量架构,能够极…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...
