基于动态规划算法的DNA序列比对函数,给出两条序列(v和w)的打分矩阵
一.什么是动态规划算法
1.1总体思想
·动态规划算法与分治法类似,基本思想也是将待求解的问题分成若干个子问题
·经过分解得到的子问题往往不是互相独立的,有些子问题被重复计算多次
·如果能够保存已解决的子问题答案,在需要时再找出来已求得的答案,就可以避免大量重复计算,从而得到多项式时间算法(备忘录)
1.2使用动态规划求解的问题需要具备的基本要素
1)重复子问题
·递归算法求解问题时,每次产生的子问题并不总是新问题,有些子问题被反复计算多次,这种性质被称为子问题的重叠性质
·动态规划算法,对每一个子问题只解一次,而后将其解保存在一个表格中,当再次需要解此子问题时,只是简单地用常数时间查看一下结果。
·通常不同的子问题个数随问题的大小呈多项式增长,用动态规划算法只需要多项式时间,从而获得较高的解题效率。
2)最优子结构
·一个问题的最优解包含着其子问题的最优解,这种性质称为最优子结构性质
·分析问题的最优子结构性质,首先假设由问题的最优解导出的子问题的解不是最优,然后再设法说明在这个假设下可构造出比原问题最优解更好的解,从而导致矛盾
·利用问题的最优子结构性质,以自底向上的方式递归地从子问题的最优解逐步构造出整个问题的最优解
·最优子结构是一个问题能用动态规划算法求解的前提
1.3动态规划求解的基本步骤
1)找出最优解的性质,并刻画其结构特征
2)递归地定义最优质
3)以自底向上的方式计算出最优值
4)根据计算最优值时得到的信息,构造最优解
二.打分矩阵代码
import random # 1. 生成一个指定长度的随机DNA序列
def generate_dna(length): dna_bases = 'ACGT' # DNA的四个碱基 sequence = '' # 初始化空序列 for _ in range(length): # 循环length次 sequence += random.choice(dna_bases) # 每次从四个碱基中随机选一个添加到序列中 return sequence # 返回生成的DNA序列 # 2. 在DNA序列中随机位置插入一个可能突变的motif
def insert_motif(dna, motif, mutation_rate): mutated_motif = '' # 初始化突变的motif为空字符串 for base in motif: # 遍历motif中的每个碱基 if random.random() < mutation_rate: # 如果随机数小于突变率 mutated_motif += random.choice('ACGT') # 则该位置碱基随机突变 else: mutated_motif += base # 否则保持原样 insert_point = random.randint(0, len(dna)) # 在DNA序列中随机选择一个插入点 return dna[:insert_point] + mutated_motif + dna[insert_point:] # 插入突变的motif # 3. 生成多条带有随机插入motif的DNA序列
def generate_sequences(num_sequences, dna_length, motif_length, mutation_rate): sequences = [] # 初始化一个空列表来存储生成的序列 motif = generate_dna(motif_length) # 生成一个随机的motif for _ in range(num_sequences): # 循环生成指定数量的序列 dna = generate_dna(dna_length) # 生成一个DNA序列 dna_with_motif = insert_motif(dna, motif, mutation_rate) # 插入motif sequences.append(dna_with_motif) # 将序列添加到列表中 return sequences # 返回生成的序列列表 # 使用函数生成序列并打印
sequences = generate_sequences(5, 20, 5, 0.1)
for seq in sequences: print(seq)三.编写一个函数,生成m条DNA序列,每条序列长度为k,然后对每条序列随机插入一个长度为L的motif,motif的突变率为n
import random # 1. 生成一个指定长度的随机DNA序列
def generate_dna(length): dna_bases = 'ACGT' # DNA的四个碱基 sequence = '' # 初始化空序列 for _ in range(length): # 循环length次 sequence += random.choice(dna_bases) # 每次从四个碱基中随机选一个添加到序列中 return sequence # 返回生成的DNA序列 # 2. 在DNA序列中随机位置插入一个可能突变的motif
def insert_motif(dna, motif, mutation_rate): mutated_motif = '' # 初始化突变的motif为空字符串 for base in motif: # 遍历motif中的每个碱基 if random.random() < mutation_rate: # 如果随机数小于突变率 mutated_motif += random.choice('ACGT') # 则该位置碱基随机突变 else: mutated_motif += base # 否则保持原样 insert_point = random.randint(0, len(dna)) # 在DNA序列中随机选择一个插入点 return dna[:insert_point] + mutated_motif + dna[insert_point:] # 插入突变的motif # 3. 生成多条带有随机插入motif的DNA序列
def generate_sequences(num_sequences, dna_length, motif_length, mutation_rate): sequences = [] # 初始化一个空列表来存储生成的序列 motif = generate_dna(motif_length) # 生成一个随机的motif for _ in range(num_sequences): # 循环生成指定数量的序列 dna = generate_dna(dna_length) # 生成一个DNA序列 dna_with_motif = insert_motif(dna, motif, mutation_rate) # 插入motif sequences.append(dna_with_motif) # 将序列添加到列表中 return sequences # 返回生成的序列列表 # 使用函数生成序列并打印
sequences = generate_sequences(5, 20, 5, 0.1)
for seq in sequences: print(seq)四.对生成的已插入突变motif的序列集合,编写一套函数,寻找其中的motif,可指定motif长度;
# 定义一个名为 find 的函数,它接受两个参数:
# sequence_set 是一个包含多个 DNA 序列的列表
# motif_length 是我们想要查找的子序列(也称为 motif)的长度
def find(sequence_set, motif_length): # 初始化一个空集合 motifs,用于存储找到的所有唯一的 motif motifs = set() # 遍历 sequence_set 中的每一条序列 for sequence in sequence_set: # 对于每一条序列,我们从其第一个碱基开始,直到剩下的碱基数量少于 motif_length 为止 # 这样确保我们可以从序列中提取出完整长度的 motif for i in range(len(sequence) - motif_length + 1): # 从当前位置 i 开始,提取长度为 motif_length 的子序列 motif = sequence[i:i+motif_length] # 将提取到的 motif 添加到 motifs 集合中 # 由于 motifs 是一个集合,所以重复的 motif 会被自动去除 motifs.add(motif) # 函数返回包含所有唯一 motif 的集合 return motifs # 测试数据:一个包含三条 DNA 序列的列表和一个 motif 长度值
sequence_set = ['ACGTTAGC', 'GTATCGAG', 'CGTACGTA']
motif_length = 4 # 调用 find 函数,传入测试数据,并将返回的结果存储在变量 motifs 中
motifs = find(sequence_set, motif_length)
# 打印出找到的所有唯一 motif
print(motifs)五.对生成的已插入突变motif的序列集合,编写一套函数,基于分支界定法寻找指定长度的motif,并与遍历法比较计算效率
import itertools
import time # 计算motif在序列中的得分
def calculate_score(motif, sequences): score = 0 for seq in sequences: min_distance = float('inf') for i in range(len(seq) - len(motif) + 1): distance = sum(motif[j] != seq[i + j] for j in range(len(motif))) min_distance = min(min_distance, distance) score += min_distance return score # 分支界定法
def find_motif_branch_bound(sequences, motif_length): best_motif = None best_score = float('inf') def search(motif, depth): nonlocal best_motif, best_score if depth == motif_length: score = calculate_score(motif, sequences) if score < best_score: best_score = score best_motif = motif return for base in 'ACGT': search(motif + base, depth + 1) start_time = time.time() search('', 0) end_time = time.time() return best_motif, end_time - start_time # 遍历法
def find_motif_brute_force(sequences, motif_length): best_motif = None best_score = float('inf') start_time = time.time() for motif in itertools.product('ACGT', repeat=motif_length): motif = ''.join(motif) score = calculate_score(motif, sequences) if score < best_score: best_score = score best_motif = motif end_time = time.time() return best_motif, end_time - start_time # 示例序列集合和motif长度
sequences = ['ACGTAGCTAG', 'ACGGATCGTA', 'TAGCTAGCTA', 'TCGATCGATT']
motif_length = 3 # 使用分支界定法寻找motif
motif_bb, time_bb = find_motif_branch_bound(sequences, motif_length)
print(f"Branch and Bound Motif: {motif_bb}, Time: {time_bb:.4f}s") # 使用遍历法寻找motif
motif_bf, time_bf = find_motif_brute_force(sequences, motif_length)
print(f"Brute Force Motif: {motif_bf}, Time: {time_bf:.4f}s")相关文章:
的打分矩阵)
基于动态规划算法的DNA序列比对函数,给出两条序列(v和w)的打分矩阵
一.什么是动态规划算法 1.1总体思想 动态规划算法与分治法类似,基本思想也是将待求解的问题分成若干个子问题 经过分解得到的子问题往往不是互相独立的,有些子问题被重复计算多次 如果能够保存已解决的子问题答案,在需要时再找出来已求得…...

Tailwind CSS快速入门
文章目录 初识安装Tailwindcss试用安装快速书写技巧扩展好处Todo 初识 只需书写 HTML 代码,无需书写 CSS,即可快速构建美观的网站 Tailwind CSS 是一个功能类优先的 CSS 框架,它通过提供大量的原子类(utility classes)…...
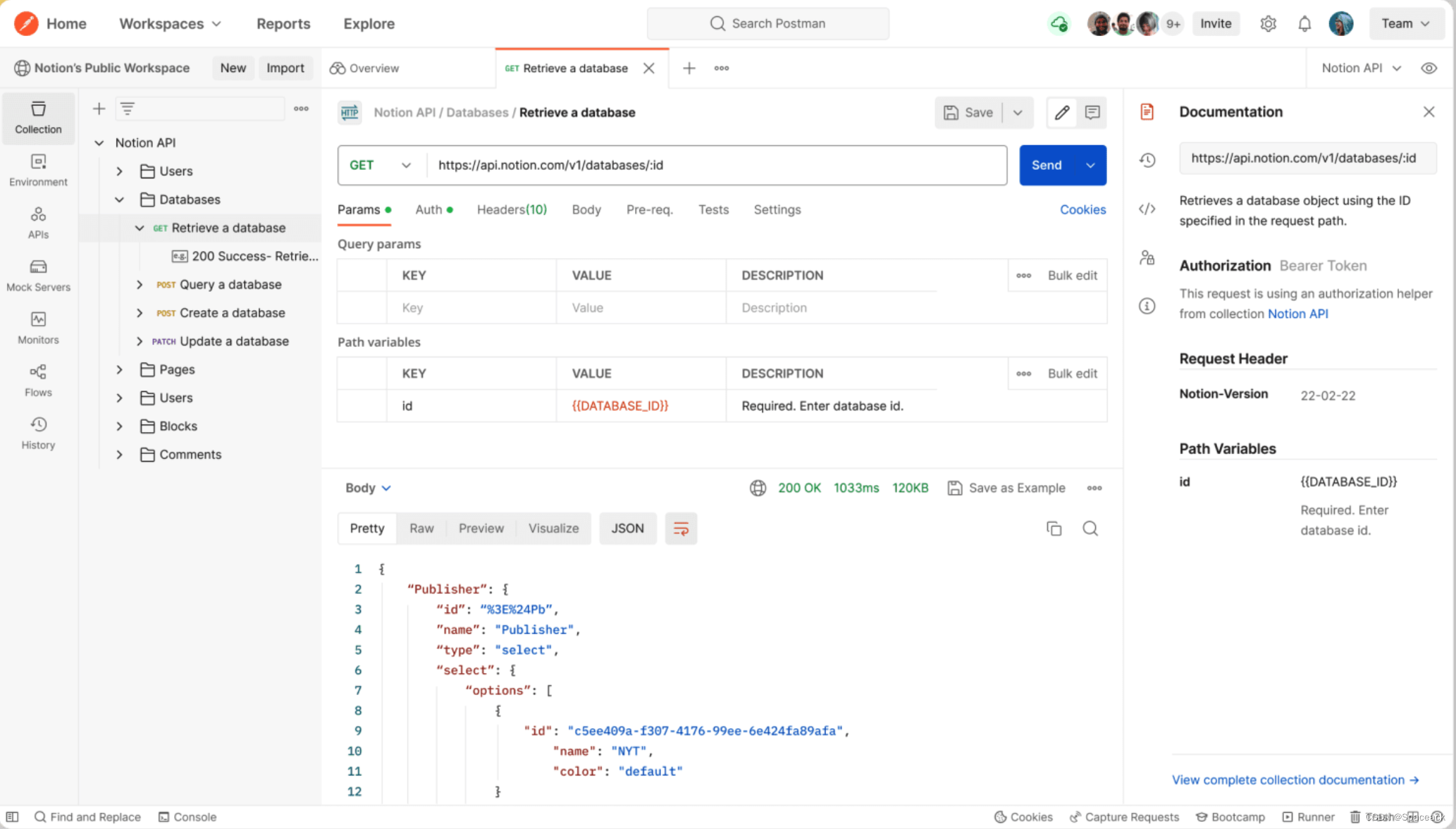
Postman使用技巧
Postman是一款广泛使用的API开发和测试工具,专为简化Web服务API的开发、测试、文档编制和协作过程而设计。它支持各种HTTP请求方法,包括GET、POST、PUT、DELETE等,允许用户轻松地构建和发送请求,以及检查响应。 本文介绍几个提升效…...

sqli-labs靶场
less---11 1.求闭合字符 输入1报错说明存在注入点 存在注入点 2.查库名 使用报错注入查库名 admin” and (select 1 from (select count(*),concat(database(),floor(rand(0)*2))x from information_schema.tables group by x)y)# //floor函数报错 3.查表名 admin and upd…...

基于springboot的大创管理系统
摘要 随着信息技术在管理上越来越深入而广泛的应用,管理信息系统的实施在技术上已逐步成熟。本文介绍了大创管理系统的开发全过程。通过分析大创管理系统管理的不足,创建了一个计算机管理大创管理系统的方案。文章介绍了大创管理系统的系统分析部分&…...

常用torch.nn
目录 一、torch.nn和torch.nn.functional二、nn.Linear三、nn.Embedding四、nn.Identity五、Pytorch非线性激活函数六、nn.Conv2d七、nn.Sequential八、nn.ModuleList九、torch.outer torch.cat 一、torch.nn和torch.nn.functional Pytorch中torch.nn和torch.nn.functional的区…...

力扣226.翻转二叉树101.对称二叉树
解决二叉树的问题,经常要习惯从递归角度思考 左子树/右子树是否具备某属性、是否属于什么类型(和题目要求的判断当前树是否xxx一样); 对左/右子树进行什么操作(和题目要求的对当前树的操作一样)。 226.翻转…...
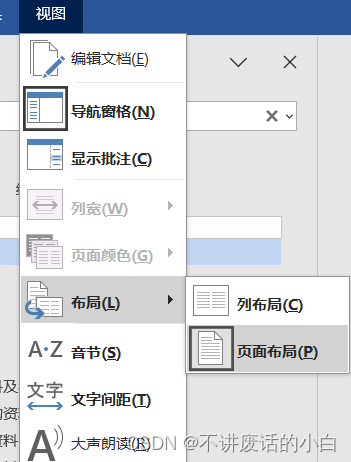
word如何按照原本页面审阅文档
1 视图-阅读视图 2 视图,自己看,懒得打字了哈哈...

前端基础入门三大核心之HTML篇:探索WebAssembly —— 开启网页高性能应用新时代
前端基础入门三大核心之HTML篇:探索WebAssembly —— 开启网页高性能应用新时代 WebAssembly基础概念工作原理概览WebAssembly实战示例基本使用 安全性与性能优化防范漏洞实践实际工作中的使用技巧结语与讨论 随着Web技术的飞速发展,前端开发者面临越来越…...
)
NDIS小端口驱动(四)
NDIS中断相关 1. 注册和取消注册中断: 微型端口驱动程序调用 NdisMRegisterInterruptEx 来注册中断。 驱动程序分配并初始化 NDIS_MINIPORT_INTERRUPT_CHARACTERISTICS 结构,以指定中断特征和函数入口点,驱动程序将结构传递给 NdisMRegister…...

用户态网络缓冲区设计
基于数组实现的环形缓冲区: 优点 使用固定大小的连续空间做用户态缓冲区,利用了内存访问的局部性,可以提高缓存命中率,提高程序性能,在处理大量数据时,缓存的利用率对性能有着很大的影响 正是基于性能的…...
)
Linux运维工程师基础面试题整理(三)
Linux运维工程师基础面试题整理(三) 1. 文件inode号有什么用?2. 文件的权限怎么设置与管理?3. 如何SSH免密配置?4. 如何快速部署一个web服务?5. 如何更新Linux系统内核?6. centos中如何配置本地yum源?7.Linux 防火墙如何简单配置?8. 有哪些工具可以批量管理Linux服务器…...
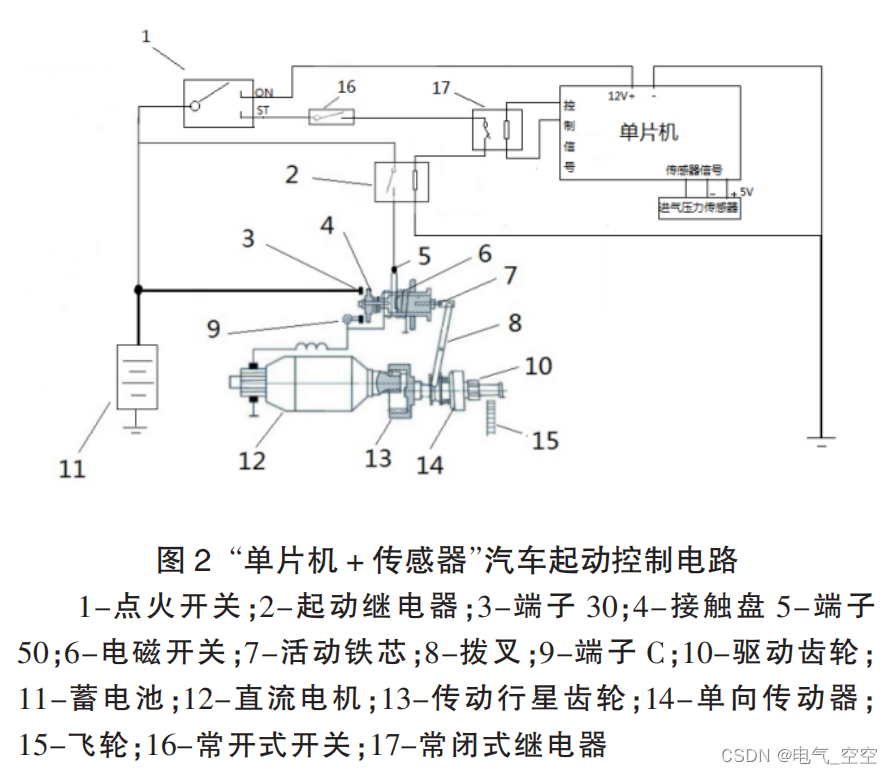
基于单片机与传感器技术的汽车起动线路设计
摘 要:在以发动机为动力源的汽车中,起动系统承担起使发动机由非工作状态进入工作状态的重要作用,属于发动机的附属系统。在传统汽车起动系统的基础上提出将单片机与传感器技术运用到起动控制线路中,通过传感器采集发动机工作状态信…...

C#如何通过反射获取外部dll的函数
在C#中,你可以使用反射(Reflection)来加载外部的DLL(动态链接库)并获取其中的函数(在C#中通常称为方法)。但是,请注意,反射主要用于访问类型信息,并且对于非托…...

从零开始傅里叶变换
从零开始傅里叶变换 1 Overview2 傅里叶级数2.1 基向量2.2 三角函数系表示 f ( t ) f(t) f(t)2.2.1 三角函数系的正交性2.2.2 三角函数系的系数 2.3 复指数函数系表示 f ( t ) f(t) f(t)2.3.1 复指数函数系的系数2.3.2 复指数函数系的正交性 2.4 傅里叶级数总结 3 傅里叶变换…...

解决1万条数据前端渲染不卡的问题
万级数据前端渲染优化 解决思路requestAnimationFrame完整代码 解决思路 将数据分组,通过定时器或requestAnimationFrame两种方式分组渲染到Dom上 requestAnimationFrame 渲染数据-动画requestAnimationFram方法 使用requestAnimationFrame可以将动画的每一帧绘制…...

如何编写一个API——Python代码示例及拓展
下面是一个必备的API的demo,包括用户认证、数据库交互、错误处理和更复杂的异步任务处理。使用Flask来创建一个RESTful API,涉及用户注册、登录、以及获取用户信息的功能。 示例1:编写API 安装依赖 首先,你需要安装以下库来支持示例的功能: pip install flask flask-c…...
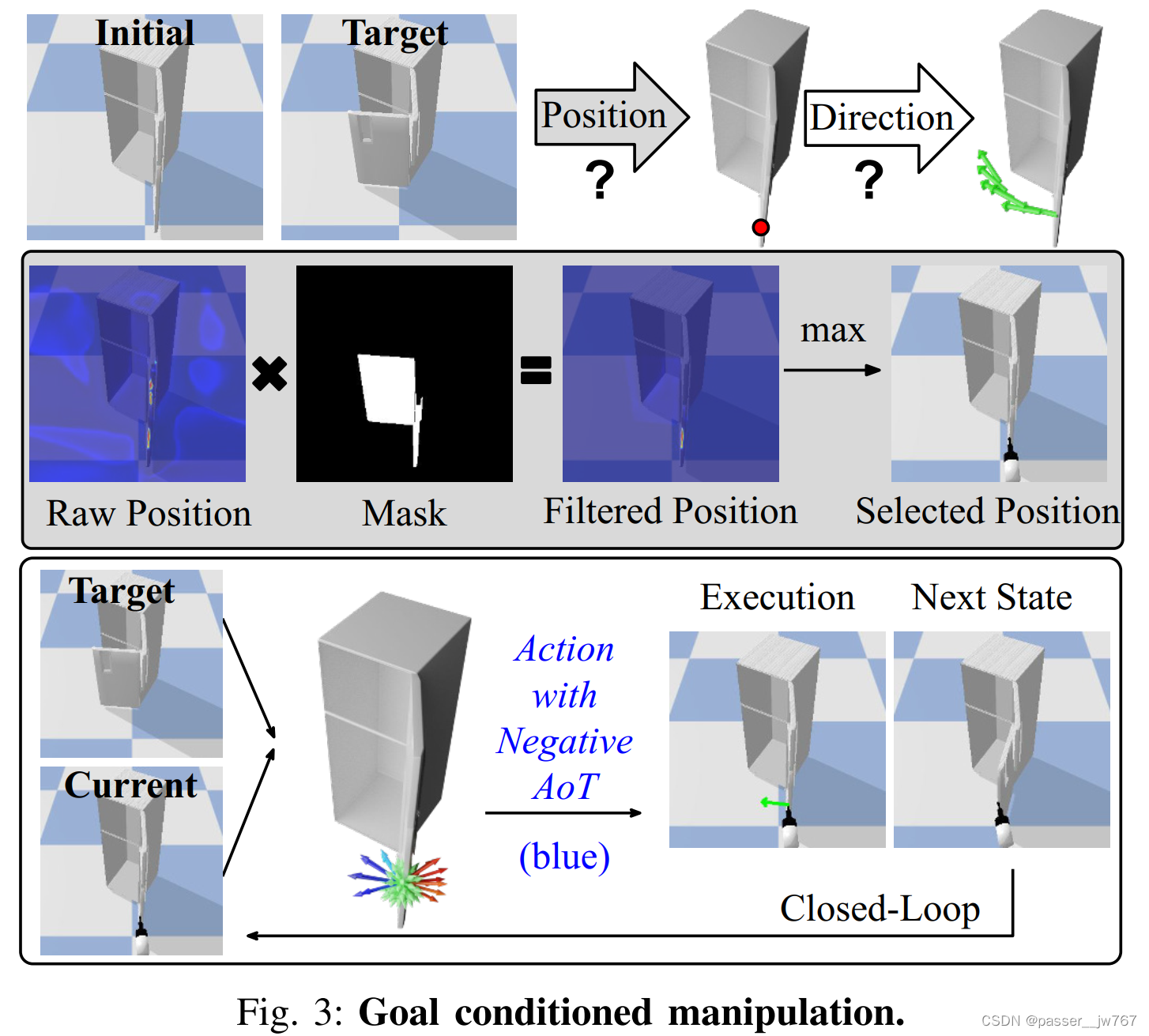
UMPNet: Universal Manipulation Policy Network for Articulated Objects
1. 摘要 UMPNet是一个基于图像的策略网络,能够推理用于操纵铰接物体的闭环动作序列。该策略支持6DoF动作表示和可变长度轨迹。 为处理多种类的物体,该策略从不同的铰接结构中学习,并泛化到未见过的物体或类别上。该策略是以自监督探索的方式…...

高通 Android 12/13冻结屏幕
冻结屏幕很多第一次听到以为是Android一种异常现象,实则不然,就是防止用户在做一些非法操作导致问题防止安全漏洞问题。 1、主要通过用户行为比如禁止下拉状态栏和按键以及onTouch事件拦截等,不知道请看这篇文章(Touch事件传递流…...

C++实现图的存储和遍历
前言 许多新手友友在初学算法和数据结构时,会被图论支配过。我这里整理了一下图论常见的存储和遍历方式,仅供参考。如有问题,欢迎大佬们批评指正。 存储我将提到四种方式:邻接矩阵、vector实现邻接表、数组模拟单链表实现的前向星…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
