LeetCode-102. 二叉树的层序遍历【树 广度优先搜索 二叉树】
LeetCode-102. 二叉树的层序遍历【树 广度优先搜索 二叉树】
- 题目描述:
- 解题思路一:一个全局队列queue,while queue:去搜集当前所有queue的level
- 解题思路二:背诵版
- 解题思路三:
题目描述:
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
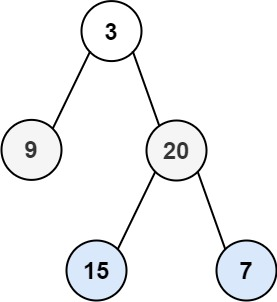
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
提示:
树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000
解题思路一:一个全局队列queue,while queue:去搜集当前所有queue的level
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:if not root:return []queue = collections.deque([root])result = []while queue:level = []for _ in range(len(queue)):cur = queue.popleft()level.append(cur.val)if cur.left:queue.append(cur.left)if cur.right:queue.append(cur.right)result.append(level)return result
时间复杂度:O(n)
空间复杂度:O(n)
解题思路二:背诵版
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:if not root:return []queue = collections.deque([root])ans = []while queue:level = []for _ in range(len(queue)):cur = queue.popleft()if cur.left:queue.append(cur.left)if cur.right:queue.append(cur.right)level.append(cur.val)ans.append(level)return ans
时间复杂度:O(n)
空间复杂度:O(n)
解题思路三:
时间复杂度:O(n)
空间复杂度:O(n)



♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠
相关文章:

LeetCode-102. 二叉树的层序遍历【树 广度优先搜索 二叉树】
LeetCode-102. 二叉树的层序遍历【树 广度优先搜索 二叉树】 题目描述:解题思路一:一个全局队列queue,while queue:去搜集当前所有queue的level解题思路二:背诵版解题思路三: 题目描述: 给你二…...

基于时频模糊算子的数据增强方法
关键词:时频模糊,数据增强,机器学习,音频预处理 我们引入时频模糊算子,该算子将信号的短时傅里叶变换与指定的核进行卷积,在SpeechCommands V2数据集上训练了一个使用ResNet-34架构的卷积神经网络(CNN)和一…...

浅谈后端整合Springboot框架后操作基础配置
boot基础配置 现在不访问端口8080 可以吗 我们在默认启动的时候访问的是端口号8080 基于属性配置的 现在boot整合导致Tomcat服务器的配置文件没了 我们怎么去修改Tomcat服务器的配置信息呢 配置文件中的配置信息是很多很多的... 复制工程 保留工程的基础结构 抹掉原始…...

英码科技算能系列边缘计算盒子再添新成员!搭载TPU处理器BM1688CV186AH,功耗更低、接口更丰富
在数据呈现指数级增长的今天,越来越多的领域和细分场景对实时、高效的数据处理和分析的需求日益增长,对智能算力的需求也不断增强。为应对新的市场趋势,英码科技凭借自身的硬件研发优势,携手算能相继推出了基于BM1684的边缘计算盒…...
selenium 爬取今日头条
由于今日头条网页是动态渲染,再加上各种token再验证,因此直接通过API接口获取数据难度很大,本文使用selenium来实现新闻内容爬取。 selenium核心代码 知识点: 代码中加了很多的异常处理,保证错误后重试,…...

docker 安装 yapi
文章目录 docker 安装 yapi一、拉取镜像二、创建目录三、添加配置文件四、初始化数据库表五、启动 yapi六、测试以及修改默认密码 没有 MongDB 的可以先看这个教程:MongDB安装教程 docker 安装 yapi 版本: 1.9.5 一、拉取镜像 docker pull yapipro/y…...
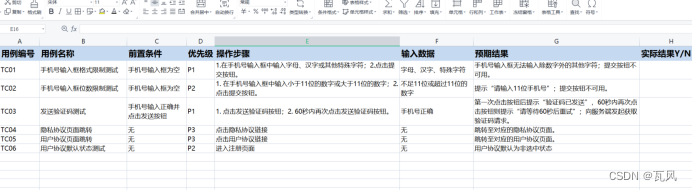
【AI如何帮你编写测试用例并输出表格格式】
1、工具:顺便使用一款生成式AI即可,此处用的是ChatGPT,Kimi这两个工具试验。 2、首先要拿到需求文档,根据需求文档向AI发出如下指令(Prompt) “请根据下面这段需求,编写测试用例: …...

九宫格转圈圈抽奖活动,有加速,减速效果
在线访问demo和代码在底部 代码,复制就可以跑 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><tit…...

利用阿里OSS服务给文件设置过期删除--简单版
在云存储广泛应用的今天,阿里云的Object Storage Service(OSS)以其高度可扩展性、安全性和成本效益,成为了众多企业和开发者存储海量数据的首选方案。随着数据量的不断膨胀,高效的数据管理和成本控制变得尤为重要。其中…...
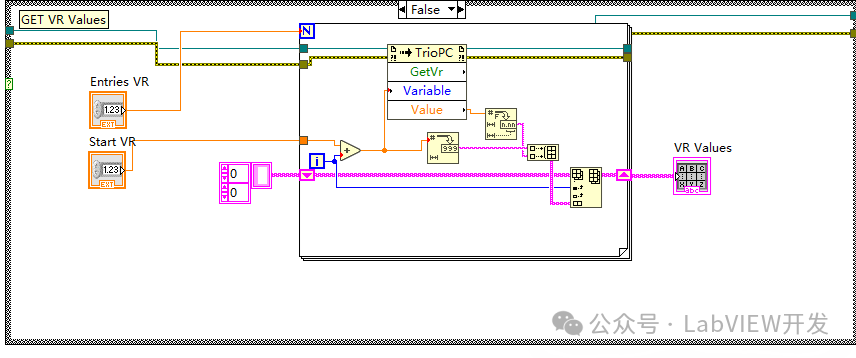
LabVIEW控制Trio控制器
将LabVIEW与Trio控制器结合,可以实现对复杂运动系统的控制和监测。以下是详细的方法和注意事项: 一、准备工作 软件安装: 安装LabVIEW开发环境,确保版本兼容性。 安装Trio控制器的相关驱动程序和软件,如Trio Motion …...
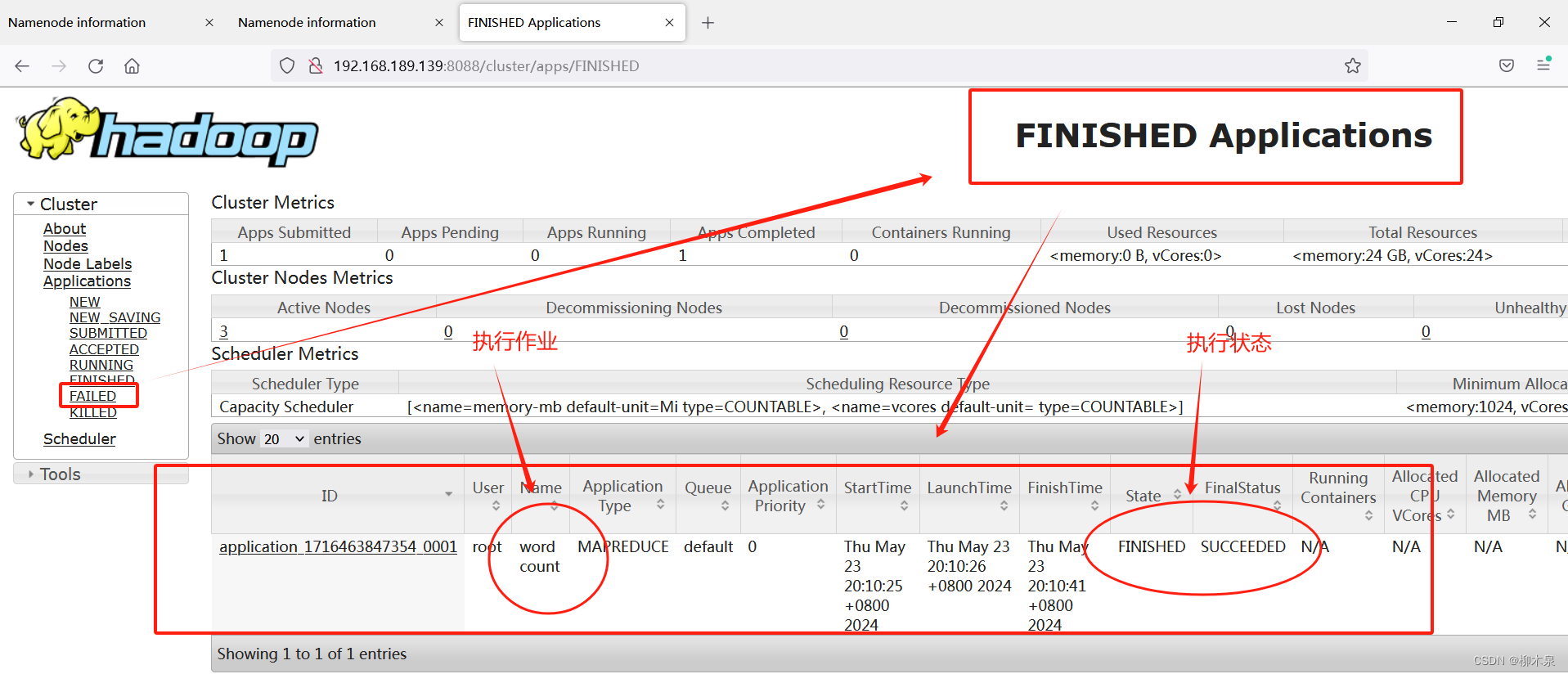
02--大数据Hadoop集群实战
前言: 前面整理了hadoop概念内容,写了一些概念和本地部署和伪分布式两种,比较偏向概念或实验,今天来整理一下在项目中实际使用的一些知识点。 1、基础概念 1.1、完全分布式 Hadoop是一个开源的分布式存储和计算框架࿰…...

【ARMv8/v9 异常模型入门及渐进 10 -- WFI 与 WFE 使用详细介绍 1】
请阅读【ARMv8/v9 ARM64 System Exception】 文章目录 WFI 与 WFE等待事件(WFE)发送事件(SEV)本地发送事件(SEVL)WFE 唤醒事件 WFE 使用场景举例与代码实现wfe睡眠函数sev 事件唤醒函数全局监视器和自旋锁 …...

@DateTimeFormat 和 @JsonFormat 的区别和使用方式
一. DateTimeFormat 详细用例 DateTimeFormat 是 Spring Framework 的一部分,它用于绑定 Web 请求中的字符串到 Java 的日期和时间类型。这种转换常常在 Spring MVC 控制器中处理 HTTP 请求参数或路径变量时使用。 使用场景: 将 HTTP 请求中的日期(也就是网络传输…...

C++—结构体
结构体(struct),是一种用户自定义复合数据类型,可以包含不同类型的不同成员。 结构体的声明定义和使用的基本语法: // 声明结构体struct 结构体类型 { 成员1类型 成员1名称; ...成员N类型 成员N名称; };除声明…...
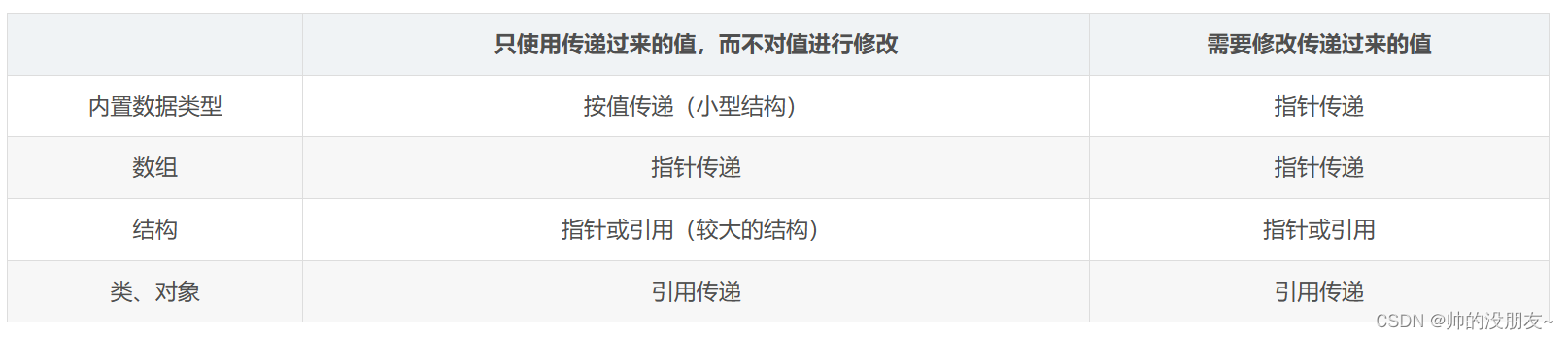
指针与引用
指针与引用 一:指针与引用场景二级目录三级目录 一:指针与引用场景 二级目录 三级目录...

使用 mysql-binlog-connector 监听处理 MySQLBinlog 文件
1. 需求概述 业务开发中经常需要根据一些数据变更实现相对应的操作。例如,一些用户注销自己的账户,系统可以给用户自动发短信确认,这时有两种解决方案,一种是耦合到业务系统中,当用户执行注销操作的时候,执…...

CF Div2 729 Plus and Multiply
原题链接:Problem - 1542B - Codeforces 题目大意:初始集合里面只有1,给a和b,可以对集合里面的数x进行二种操作,x*a,xb,并放入集合,给数n,问集合里面会不会产生n,会就输…...
Joomla 3.7.0 (CVE-2017-8917) SQL注入漏洞环境
1 漏洞概述 Joomla是一个基于PHP的内容管理系统(CMS),广泛应用于各类网站。2017年,Joomla 3.7.0版本被发现存在SQL注入漏洞(CVE-2017-8917),攻击者可以利用该漏洞对数据库进行未授权查询或操作…...

Python高克勒-曼宁-斯特里克勒公式计算一维流量
📜曼宁公式-用例 📜Python流体数据统计模型和浅水渗流平流模型模拟 | 📜Python蒸发散物理问题(微积分-线性代数-拉普拉斯和傅立叶变换) ✒️Python计算一维流量 高克勒-曼宁-斯特里克勒公式公式基于一维(横截面平均)…...
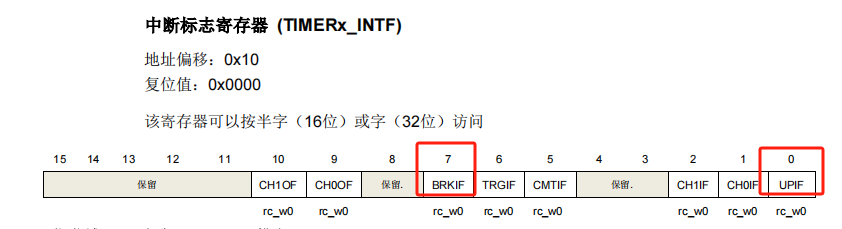
【GD32系列--基本定时器Timer + 定时1ms 灯光间隔1s闪烁例程】
这里写目录标题 一、定时器的作用二、定时器简介1、定时器类型2、时钟树3、定时器功能配置框图 三、定时器寄存器分析1、控制寄存器(TIMERx_CTL0))2、DMA 和中断使能寄存器 (TIMERx_DMAINTEN)3、预分频寄存器 (TIMERx_PSC)4、计数器自动重载寄存器 (TIME…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
