数据结构---树,二叉树的简单概念介绍、堆和堆排序
树
树的概念和结构
结构
在我们将堆之前,我们先来了解一下我们的树。
我们的堆是属于树里面的一种,
树是一种非线性结构,是一种一对多的一种结构,也就是我们的一个节点可能有多个后继节点,当然也可以只有一个或者没有。我们的这些有限结点组成一个具有层次关系的集合,我们把它叫做树是因为他的结构和一颗倒挂的数很像。
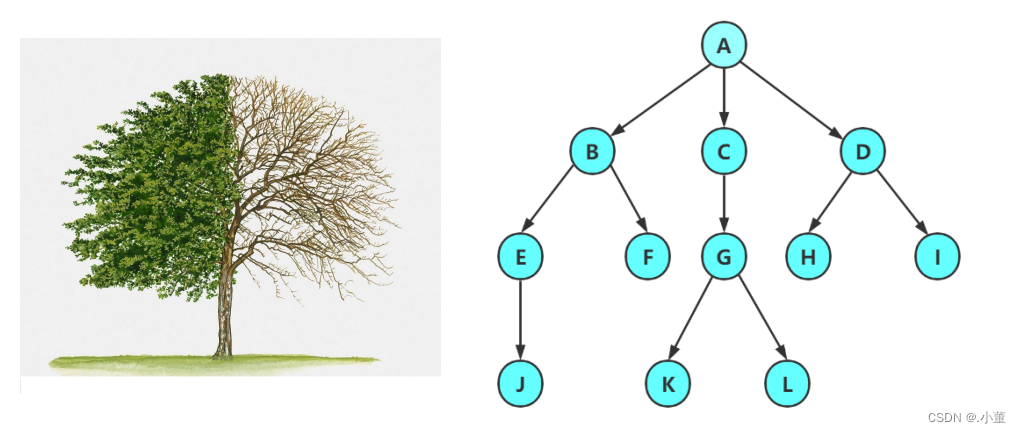
- 在我们的最上面的节点叫做根节点,他没有前驱。
- 我们树的其他节点具有0个或者多个后继节点。但是在只有一个前驱节点。
- 因此,树是递归定义的。
- 数的子树是不能相交的。相交的话就是不是我们的树了,是另外一种结构–图。
树的一些概念
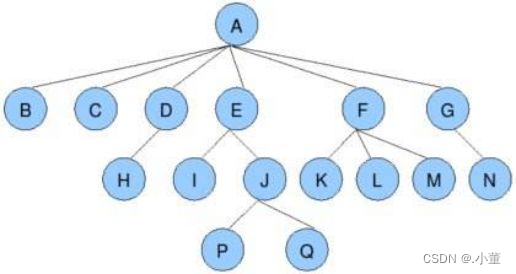
**结点的度:**一个结点含有的子树的个数称为该结点的度;
如上图:A的为6
叶结点或终端结点:度为0的结点称为叶结点; 如上图:B、C、H、I…等结点为叶结点
非终端结点或分支结点:度不为0的结点; 如上图:D、E、F、G…等结点为分支结点
**双亲结点或父结点:**若一个结点含有子结点,则这个结点称为其子结点的父结点; 如上图:A是B的父结点
**孩子结点或子结点:**一个结点含有的子树的根结点称为该结点的子结点; 如上图:B是A的孩子结点
**兄弟结点:**具有相同父结点的结点互称为兄弟结点; 如上图:B、C是兄弟结点
**树的度:**一棵树中,最大的结点的度称为树的度; 如上图:树的度为6
**结点的层次:**从根开始定义起,根为第1层,根的子结点为第2层,以此类推;
**树的高度或深度:**树中结点的最大层次; 如上图:树的高度为4
堂兄弟结点:双亲在同一层的结点互为堂兄弟;如上图:H、I互为兄弟结点
**结点的祖先:**从根到该结点所经分支上的所有结点;如上图:A是所有结点的祖先
子孙:以某结点为根的子树中任一结点都称为该结点的子孙。如上图:所有结点都是A的子孙
**森林:**由m(m>0)棵互不相交的树的集合称为森林;
树的表示
我们的树由于太过于有多个后继节点导致我们的树在构建的时候会比较麻烦,我们可以用我们的链表来表示,也可以用数组来表示。
链式
对与我们用链式来存储我们的树的话,就需要我们去去存储他的后继节点,但是我们这里的节点的每个后继节点数目不同,我们治理有一下个很好的方法-----孩子兄弟表示法。
就是我们只存下我们的第一个孩子节点,在定义一个兄弟节点,指向他的兄弟 节点,这样当我们的节点具有同一个节点时候我们第一个孩子节点就会是这个孩子链的头结点,我们沿着我们的兄弟指针就可以找到双亲的所有孩子节点。
typedef int DataType;
struct Node
{struct Node* firstChild1; // 第一个孩子结点struct Node* pNextBrother; // 指向其下一个兄弟结点DataType data; // 结点中的数据域
};
数组
我们这里用数组存储主要是利用了双亲和孩子节点的下标关系。主要是存储二叉树的。
二叉树的相关知识
一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 由一个根结点加上两棵别称为左子树和右子树的二叉树组成

特点:
3. 二叉树不存在度大于2的结点
4. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
一张有意思的图:


**特殊的二叉树:
**
- **满二叉树:**一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是
说,如果一个二叉树的层数为K,且结点总数是 ,则它就是满二叉树。 - **完全二叉树:**完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对
应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

二叉树的性质
- 若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有 个结点.
- 若规定根结点的层数为1,则深度为h的二叉树的最大结点数是 .2^(
- 对任何一棵二叉树, 如果度为0其叶结点个数为 n1, 度为2的分支结点个数为n2 ,则有 n2=n1 +1
- 对于孩子和双亲的关系,如果我们给每个节点都标都标上序号的话,如果为空我们也还是要为那个空节点保留下这个序号,我们就可以发现一个双亲和他们的孩子节点的下标关系**:左孩子=父亲+1;右孩子=父亲+2;**
由于我们整数激素那取整 的关系,我们利用孩子节点来求我们的父亲就可以写成:父亲=(孩子-1)/2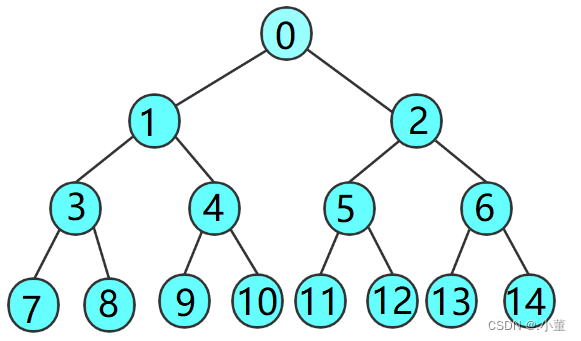
- 若规定根结点的层数为1,具有n个结点的满二叉树的深度,h= . (ps: 是log以2为底,n+1为对数)。
数组存储二叉树
我使用数组存储还是利用了二叉树的那条双亲和孩子的序号关系,我的通过计算下标就可以找到他们的双亲节点和孩子节点。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
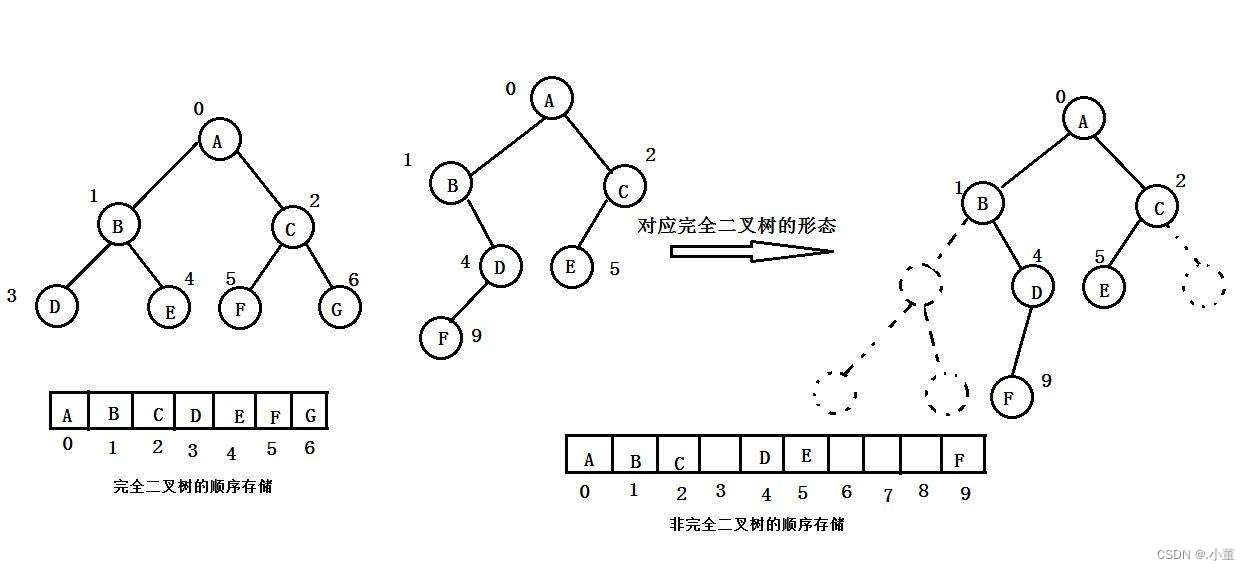
如果我们的二叉树是一颗完全二叉树的话我们可以考虑用数组去存储,这样操作起来会方便很多。
当然我们的树越接近满二叉树,我们的数组存储效率会很高,空间浪费的会很少。但是我们的二叉树的不是一个完全二叉树的话我们的存储效率会低很多,我峨嵋你要按照双亲的关系来存储。那么那些空姐带你的地方我们是不可以存储值的。
下面我们要讲的堆就是一颗完全二叉树,适合用我们的数组去存储。
堆
堆的概念及结构
如果有一个关键码的集合K = { , , ,…, },把它的所有元素按完全二叉树的顺序存储方式存储
在一个一维数组中,并满足: <= 且 <= ( >= 且 >= ) i = 0,1,2…,则称为小堆(或大堆)。将根结点最大的堆叫做最大堆或大根堆,根结点最小的堆叫做最小堆或小根堆。
总来说就是我们的双亲节点的值总是大于(小于)我们的孩子节点,
如果双亲总是大于我们的孩子节点就是大堆;
双亲小于孩子节点的话就是小堆;
现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统
虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
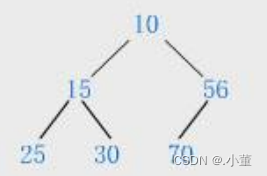
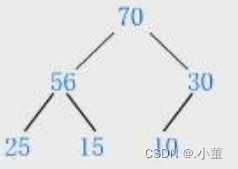
第一个是小堆,第二个是大堆。
堆的性质:
- 堆中某个结点的值总是不大于或不小于其父结点的值;
- 堆总是一棵完全二叉树。
堆的实现
我们实现我们的堆采用的是数组去存储的,维护我们堆的结构体:
typedef int HPDataType;
typedef struct Heap
{HPDataType* _a;int _size;//数组里面有多少个有效数值int _capacity;//数组的空间大小
}Heap;我们下面将我们堆实现的一些接口:
void HeapInit(Heap* php);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);
//进行调整(小堆),向上调整
void AdjustUp(HPDataType* data, int child);
//交换
void Swag(int* a, int* b);
//向下调整
void AdjustDown(HPDataType* data, int parents, int size);
初始化
我们的初始化就是给我们结构体中的数组开辟空间,不开也行,给我们的指针置空。
代码:
//堆的初始化
void HeapInit(Heap* php)
{assert(php);php->_a = (HPDataType*)malloc(sizeof(HPDataType) * 4);php->_capacity = 4;php->_size = 0;
}
堆的销毁
我们的销毁就是将我们的申请的空间还给我们的操作系统就行,我们这里主要申请的空间就是我们的数组,只需要将我们的数组释放就行。
代码:
// 堆的销毁
void HeapDestory(Heap* hp)
{assert(hp);free(hp->_a);hp->_capacity = 0;hp->_size = 0;
}
堆的向下调整算法
我们的向下调整算法,有一个前提是L他们需要左右子树必须是堆,才好去调整。
int array[] = {27,15,19,18,28,34,65,49,25,37};我们这里建小堆
当我们的左右子树不是堆的时候就会导致他们的父子关系变化。
我们向下建堆的思想是我们的根和他的孩子中较小的进行比较,如果他大于那个较小的孩子就进行交换,,交换后该节点再继续和他交换后的新的孩子进行比较,如此一直到我们的这个节点小于他的较小的孩子节点或者一直到超出我们的书的最后的一个节点的下标(就是在我们树的最后一层,他没有孩子节点了)。
例子:

我们的小堆有一个特点是:我们的根节点是堆中最小的数值,这是因为我们的父亲节点一定小于孩子节点。
我峨嵋你大堆就是根接待你是数值最大的。
代码:
//向下调整,小堆
void AdjustDown(HPDataType* data, int parents,int size)
{assert(data);int child = parents * 2 + 1;while (child <= size-1){if ( child + 1 <= size - 1 && data[child] > data[parents * 2 + 2])child = parents * 2 + 2;if (data[child] < data[parents]){//双亲比孩子大,交换Swag(&data[child], &data[parents]);}else {break;}parents = child;child = parents * 2 + 1;}
}
堆的向上调整算法
我们的向上调整算法是从我们的最后一个节点来进行的。 我们找到最后一个节点的父亲(通过他们的下标的关系),我们将该节点进行比较,如果我们的节点比他的父亲节点小就进行交换,我们再继续和他的新父亲节点进行比较,一直到他的父亲节点小于他,或者我们这个节点来到了我们根节点的位置。
这里需要注意的循环条件的判定,如果你是>=0的话就会导致死循环,当年我们该节点来到我们的根节点位置下标为0,南无我们用公式去算他的父亲节点:(0-1)/2,由于取整的特点,这个的值还会是0,并不会小于0;
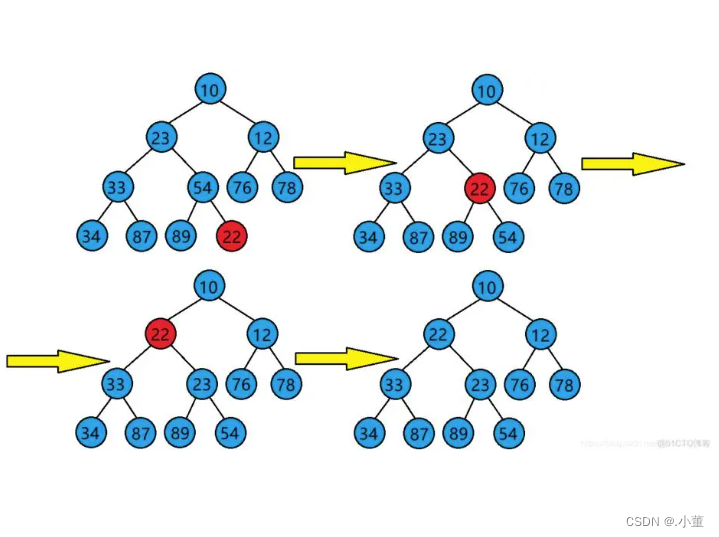
代码:
//向上调整(小堆)
void AdjustUp(HPDataType* data,int child)
{int parents = (child - 1) / 2;while (child > 0){if (data[child] < data[parents]){//双亲大于孩子,要交换Swag(&data[child], &data[parents]);child = parents;parents = (parents - 1) / 2;}else {break;}}
}
往堆中插入
我们往堆中插入是先将我们的插入的元素放在我们的数组的最后一个位置。我们插入了之后还要是我们的数组仍然是个堆,我们还要进行向上调整的操作,我们只需要调整刚进入的新的元素。形成一个新的堆。
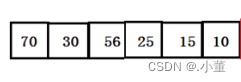

代码:
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{assert(hp);int child = hp->_size;//判断空间是否充足if (hp->_capacity == hp->_size){hp->_capacity = hp->_capacity * 2;hp->_a = (HPDataType*)realloc(hp->_a, sizeof(HPDataType) * hp->_capacity);if (hp == NULL){perror("hp realloc!");return;}}//插入新的数据hp->_a[hp->_size] = x;hp->_size++;//小堆进行调整AdjustUp(hp->_a,child);}
堆中元素的删除
我们删除元素如果删除我们的叶子节点显然是很容易的,所以我们要删除的我们的根节点。
但是如果我们的将我们的根节点删除的话,父子关系也会变乱,出现了你的兄弟节点成为了你的父亲节点,所以我们要先将我们的根节点和我们最后一个节点进行交换,再将我们的数组的大小改变,并不需要我们将值进行改变。交换之后,我们的数组也不是一个堆了,但是他的左右子树仍旧是一个小堆,这是我们就可以进行向下调整,重新将我们的数组变成一个新的堆。
代码:
// 堆的删除
void HeapPop(Heap* hp)
{//将根上面的值与我们的最后一个节点交换,在进行调整assert(hp);Swag(&hp->_a[0], &hp->_a[hp->_size - 1]);hp->_size--;AdjustDown(hp->_a,0, hp->_size);}
取堆顶的数据
我们只需要将我们的数组中下标为0的元素返回就行
代码:
HPDataType HeapTop(Heap* hp)
{assert(hp);return hp->_a[0];
}
堆的判空和数据个数
我们结构体中定义了一个size变量来记录我们元素的个数,只需要对这个只进行判断是否为0,
// 堆的数据个数
int HeapSize(Heap* hp) {assert(hp);return hp->_size;
}
// 堆的判空
int HeapEmpty(Heap* hp)
{assert(hp);return hp->_size == 0 ? 1 : 0;
}
相关文章:

数据结构---树,二叉树的简单概念介绍、堆和堆排序
树 树的概念和结构 结构 在我们将堆之前,我们先来了解一下我们的树。 我们的堆是属于树里面的一种, 树是一种非线性结构,是一种一对多的一种结构,也就是我们的一个节点可能有多个后继节点,当然也可以只有一个或者没…...
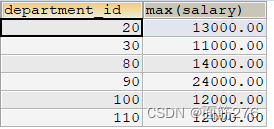
MySQL聚合函数(多行函数)
聚合函数(多行函数) 聚合函数作用于一组数据,并对一组数据返回一个值。 常见聚合函数 AVG和SUM函数 只作用于数值类型数据,不包含NULL 求工资平均值和总和 MIN和MAX函数 可以作用于任何数据类型(如字符串,…...

智慧教室课堂-专注度及考试作弊系统、课堂动态点名,情绪识别、表情识别和人脸识别结合
课堂专注度分析: 课堂专注度表情识别 作弊检测: 关键点计算方法 转头(probe)低头(peep)传递物品(passing) 侧面的传递物品识别 逻辑回归关键点 使用: 运行setup.py安装必要内容 python setup.py build develop 运行demo_inference.py 将…...

单例模式简要介绍
学习目标: 单例模式 学习内容: 单例模式(Singleton Pattern)是一种设计模式,其主要目的是确保一个类只有一个实例,并且提供一个全局的访问点。它常用于需要全局唯一对象的场景,例如日志记录器、…...
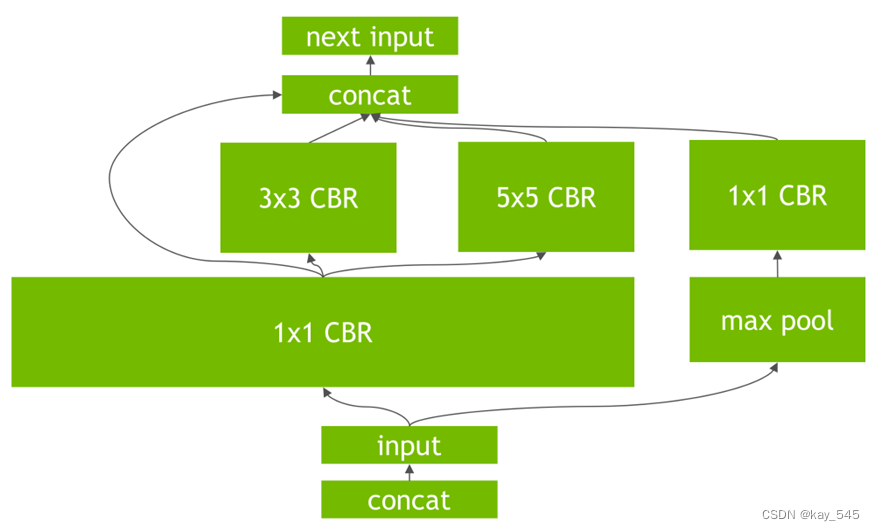
深度学习面试问题总结(21)| 模型优化
本文给大家带来的百面算法工程师是深度学习模型优化面试总结,文章内总结了常见的提问问题,旨在为广大学子模拟出更贴合实际的面试问答场景。在这篇文章中,我们还将介绍一些常见的深度学习面试问题,并提供参考的回答及其理论基础&a…...

4月手机行业线上市场销售数据分析
政府对智能手机行业的支持政策,如5G推广,以及相关的产业政策,都在一定程度上推动了智能手机市场的发展,再加上AI应用的推广和全球科技迅猛发展,中国手机市场在2024年迎来了恢复性增长。 据鲸参谋数据统计,…...

首都师范大学聘请旅美经济学家向凌云为客座教授
2024年4月17日,首都师范大学客座教授聘任仪式在首都师范大学资源环境与旅游学院举行。首都师范大学资源环境与旅游学院院长吕拉昌主持了仪式,并为旅美经济学家向凌云教授颁发了聘书。 吕拉昌院长指出,要贯彻教育部产学研一体化战略࿰…...

多电脑共享鼠标键盘
由于要在两个电脑之间共用一套鼠标键盘,所以在此记录一下。 mouse without borders Mouse without Borders 是一款免费的 Windows 工具,允许你在多台电脑之间共享鼠标和键盘。 安装与配置步骤 下载和安装: 前往 Mouse without Borders 官…...

展厅设计对企业有哪些作用
1、增强品牌形象 企业展厅对于增强企业品牌形象、提升企业的知名度和市场竞争力具有显著作用和意义。展厅作为企业对外的窗口,是客户和访客了解企业的第一印象。通过独特的设计风格和精心的展示布局,企业可以将自身的核心价值和文化理念巧妙地融入到展厅…...

LeetCode-102. 二叉树的层序遍历【树 广度优先搜索 二叉树】
LeetCode-102. 二叉树的层序遍历【树 广度优先搜索 二叉树】 题目描述:解题思路一:一个全局队列queue,while queue:去搜集当前所有queue的level解题思路二:背诵版解题思路三: 题目描述: 给你二…...

基于时频模糊算子的数据增强方法
关键词:时频模糊,数据增强,机器学习,音频预处理 我们引入时频模糊算子,该算子将信号的短时傅里叶变换与指定的核进行卷积,在SpeechCommands V2数据集上训练了一个使用ResNet-34架构的卷积神经网络(CNN)和一…...

浅谈后端整合Springboot框架后操作基础配置
boot基础配置 现在不访问端口8080 可以吗 我们在默认启动的时候访问的是端口号8080 基于属性配置的 现在boot整合导致Tomcat服务器的配置文件没了 我们怎么去修改Tomcat服务器的配置信息呢 配置文件中的配置信息是很多很多的... 复制工程 保留工程的基础结构 抹掉原始…...

英码科技算能系列边缘计算盒子再添新成员!搭载TPU处理器BM1688CV186AH,功耗更低、接口更丰富
在数据呈现指数级增长的今天,越来越多的领域和细分场景对实时、高效的数据处理和分析的需求日益增长,对智能算力的需求也不断增强。为应对新的市场趋势,英码科技凭借自身的硬件研发优势,携手算能相继推出了基于BM1684的边缘计算盒…...
selenium 爬取今日头条
由于今日头条网页是动态渲染,再加上各种token再验证,因此直接通过API接口获取数据难度很大,本文使用selenium来实现新闻内容爬取。 selenium核心代码 知识点: 代码中加了很多的异常处理,保证错误后重试,…...

docker 安装 yapi
文章目录 docker 安装 yapi一、拉取镜像二、创建目录三、添加配置文件四、初始化数据库表五、启动 yapi六、测试以及修改默认密码 没有 MongDB 的可以先看这个教程:MongDB安装教程 docker 安装 yapi 版本: 1.9.5 一、拉取镜像 docker pull yapipro/y…...
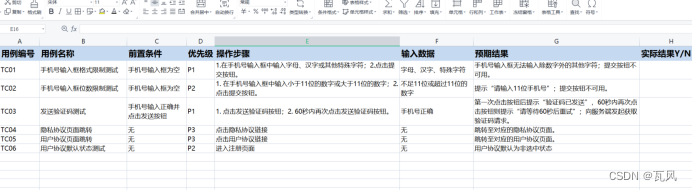
【AI如何帮你编写测试用例并输出表格格式】
1、工具:顺便使用一款生成式AI即可,此处用的是ChatGPT,Kimi这两个工具试验。 2、首先要拿到需求文档,根据需求文档向AI发出如下指令(Prompt) “请根据下面这段需求,编写测试用例: …...

九宫格转圈圈抽奖活动,有加速,减速效果
在线访问demo和代码在底部 代码,复制就可以跑 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><tit…...

利用阿里OSS服务给文件设置过期删除--简单版
在云存储广泛应用的今天,阿里云的Object Storage Service(OSS)以其高度可扩展性、安全性和成本效益,成为了众多企业和开发者存储海量数据的首选方案。随着数据量的不断膨胀,高效的数据管理和成本控制变得尤为重要。其中…...
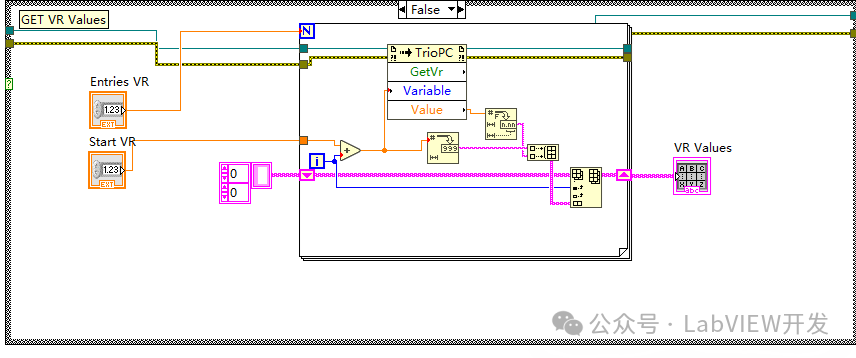
LabVIEW控制Trio控制器
将LabVIEW与Trio控制器结合,可以实现对复杂运动系统的控制和监测。以下是详细的方法和注意事项: 一、准备工作 软件安装: 安装LabVIEW开发环境,确保版本兼容性。 安装Trio控制器的相关驱动程序和软件,如Trio Motion …...
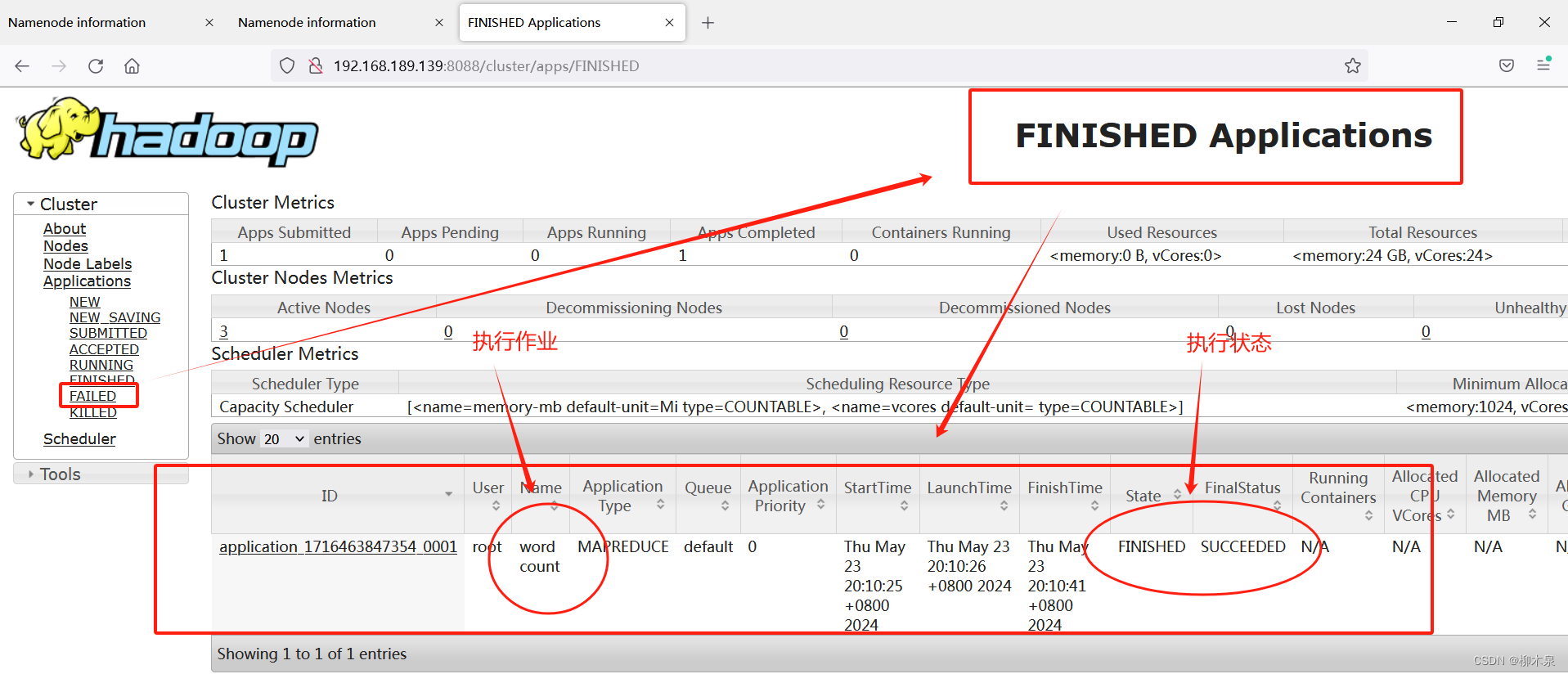
02--大数据Hadoop集群实战
前言: 前面整理了hadoop概念内容,写了一些概念和本地部署和伪分布式两种,比较偏向概念或实验,今天来整理一下在项目中实际使用的一些知识点。 1、基础概念 1.1、完全分布式 Hadoop是一个开源的分布式存储和计算框架࿰…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...

深入解析 ReentrantLock:原理、公平锁与非公平锁的较量
ReentrantLock 是 Java 中 java.util.concurrent.locks 包下的一个重要类,用于实现线程同步,支持可重入性,并且可以选择公平锁或非公平锁的实现方式。下面将详细介绍 ReentrantLock 的实现原理以及公平锁和非公平锁的区别。 ReentrantLock 实现原理 基本架构 ReentrantLo…...
