Matlab 2023b学习笔记1——界面认识
下载安装好Matlab后,可以看到如下界面:

可以看到,这时只有命令行窗口。我们在上方工具栏中选择“布局”—— “默认”,即可看到左右两边多出来了“当前文件夹”与“工作区”两栏。

一、当前文件夹界面
这个界面显示的是当前目录下的所有内容,因为此时文件夹是空的,所以没有东西。我们可以在该栏上方的横框中找到当前目录,我这里的是“C:\Users\19681\Desktop\matlab”。
二、命令行窗口
这个是一个对话式程序框,我们在里面随便输入表达式,按下“Enter”即可看到结果:

在命令行中输入“clc”并按下回车,即可清楚该窗口的所有内容。
三、 编辑器窗口
在上方工具栏中选择“新建”——“脚本”,成功后可以看到跳出来的窗口:

我们的程序一般在这里编写 。上方的“untitled”表示的是它的文件名。我们随便在里面写点什么东西,可以看到文件名右边多了个星号,这代表着我们的文件有没有被保存的内容。这时按下“crtl+s”即可进行保存。此时需要对文件进行命名,也就引出了Matlab的命名规则。
注:严格意义上来讲是变量的命名规则,文件的命名不受影响,但为了保险起见,仍然建议按照变量的命名规则来命名文件。
四、Matlab变量命名规则
1、变量名区分大小写


通过上述命令行代码可以看出,Matlab中的变量是区分大小写的。
2、变量名长度不超过63位(2012版本的规定),但建议沿用
3、变量名以字母开头,可以由字母、数字和下划线组成,但不能使用标点
4、变量名应该简洁明了,通过变量名可以直观看出变量所表示的物理意义
相关文章:

Matlab 2023b学习笔记1——界面认识
下载安装好Matlab后,可以看到如下界面: 可以看到,这时只有命令行窗口。我们在上方工具栏中选择“布局”—— “默认”,即可看到左右两边多出来了“当前文件夹”与“工作区”两栏。 一、当前文件夹界面 这个界面显示的是当前目录下…...

C++ sort排序的总和应用题
第1题 sort排序1 时限:1s 空间:256m 输入n个数,将这n个数从小到大排序,输出。 输入格式 第1行,一个正整数n(n<100) 第2行,n个正整数,小于100 输出格式 n个整…...

[力扣]——231.2的幂
题目描述: 给你一个整数 n,请你判断该整数是否是 2 的幂次方。如果是,返回 true ;否则,返回 false 。 如果存在一个整数 x 使得 n 2x ,则认为 n 是 2 的幂次方。 bool isPowerOfTwo(int n){ if(n0)retur…...

【css】引入背景图时候,路径写入@会报错
看报错信息 我的写法 解决办法 在前面加个~...

【有手就行】使用你自己的声音做语音合成,CPU都能跑,亲测有效
此文介绍在百度飞桨上一个公开的案例,亲测有效。 厌倦了前篇一律的TTS音色了吗?打开短视频听来听去就是那几个声音,快来试试使用你自己的声音来做语音合成吧!本教程非常简单,只需要你能够上传自己的音频数据就可以(建议…...

《ESP8266通信指南》番外-(附完整代码)ESP8266获取DHT11接入(基于Lua)
前言 此篇为番外篇,是 ESP8266 入门的其他功能教程,包括但不限于 DHT11 驱动TCP 通信Thingsboard 平台的接入阿里云物联网云平台接入华为云平台接入 1. 小节目标 使用 Lua 驱动 DHT11 传感器,获取温湿度的值 2. 进入主题 NodeMCU 基于 LUA 相关资料 官方文档:…...
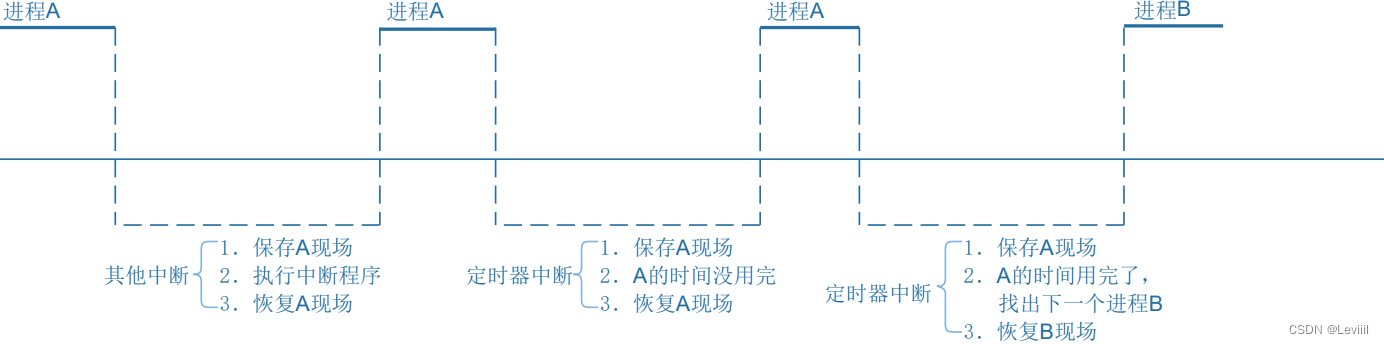
[IMX6ULL驱动开发]-Linux对中断的处理(一)
目录 中断概念的引入 ARM架构中断的流程 异常向量表 Linux系统对中断的处理 ARM对程序和中断的处理 Linux进程中断处理 中断概念的引入 如何理解中断,我们可以进行如下抽象。把CPU看做一个母亲,当它正在执行任务的时候,可以看为是一个母…...
)
PHP基础学习笔记(面向对象OOP)
类和对象 <?php //声明一个名为 Fruit 的类,它包含两个属性($name 和 $color)以及两个用于设置和获取 $name 属性的方法 set_name() 和 get_name(): class Fruit {// Propertiespublic $name;public $color;// Methodsfuncti…...
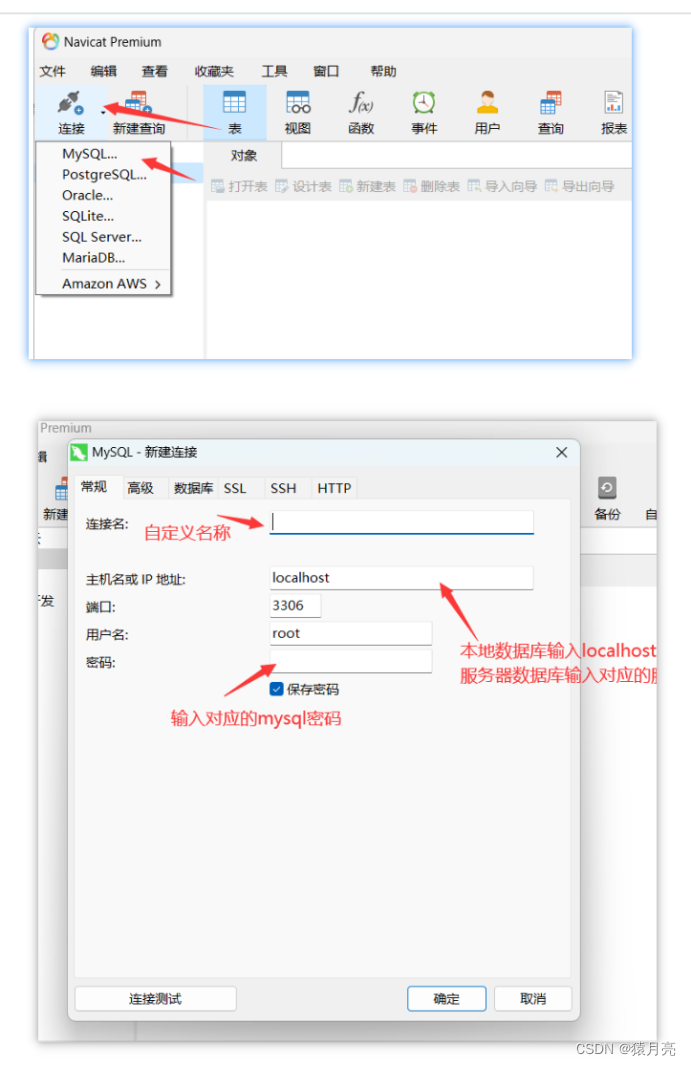
Mysql超详细安装配置教程(保姆级图文)
MySQL是一种流行的开源关系型数据库管理系统,它广泛用于网站和服务的数据存储和管理。MySQL以其高性能、可靠性和易用性而闻名,是许多Web应用程序的首选数据库解决方案之一。 一、下载安装包 (1)从网盘下载安装文件 点击此处直…...
HR招聘测评,如何判断候选人的团队协作能力?
什么是团队协作能力? 团队协作能力,说的是在集体环境中,能同他人协同工作,为追求共同的目标而努力,其中包括沟通,表达,协调,尊重,信任,责任共担等一系列综合…...
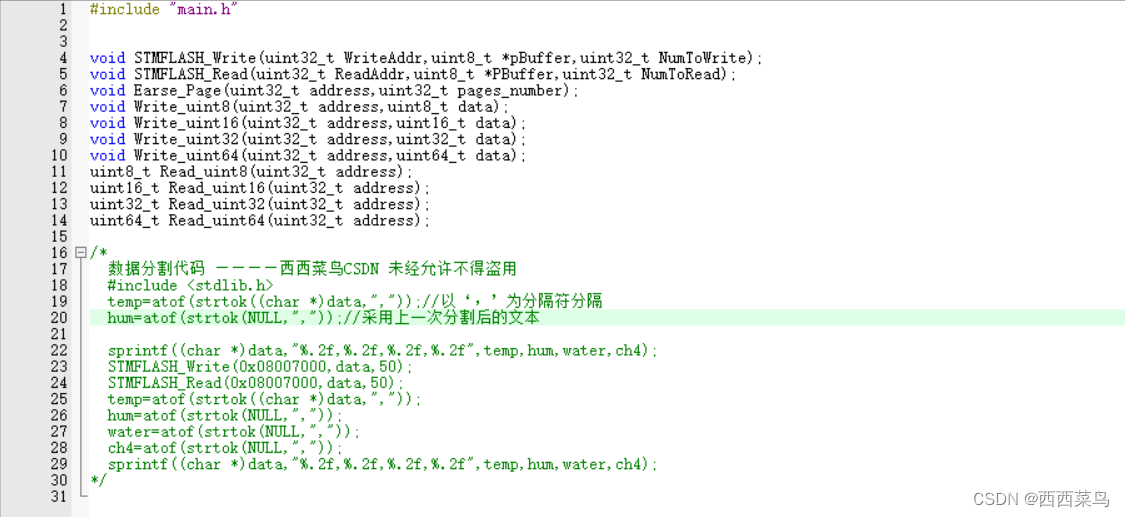
[STM32-HAL库]Flash库-HAL库-复杂数据读写-STM32CUBEMX开发-HAL库开发系列-主控STM32F103C6T6
目录 一、前言 二、实现步骤 1.STM32CUBEMX配置 2.导入Flash库 3.分析地址范围 4.找到可用的地址 5.写入读取普通数据 6.写入读取字符串 6.1 存储相关信息 6.2 存取多个参数 三、总结及源码 一、前言 在面对需要持久化存储的数据时,除了挂载TF卡,我们…...

windows 下访问 csdn 异常问题
windows下访问csdn可能会出现什么 确认是真人 或着直接连接不上的情况, 需要在 C:\Windows\System32\drivers\etc 路径下 hosts文件中添加如下内容 1.180.18.85 blog.csdn.net 如果目录下没有hosts文件就自己建一个...
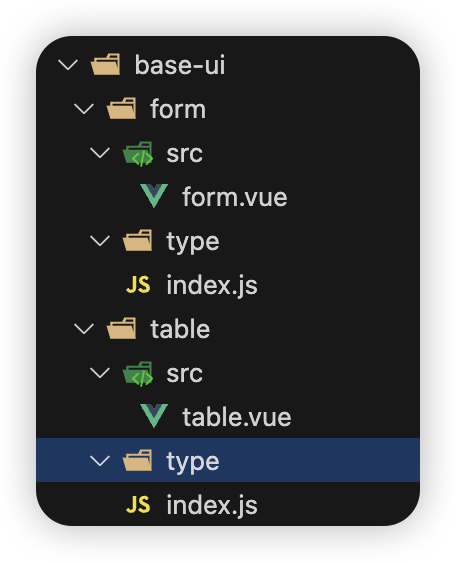
vue3结合element-plus之如何优雅的使用表格
背景 表格组件的使用在后台管理系统中是非常常见的,但是如果每次使用表格我们都去一次一次地从 element-plus 官网去 复制、粘贴和修改成自己想要的表格。 这样一来也说得过去,但是如果我们静下来细想不难发现,表格的使用都是大同小异的,每次都去复制粘贴,对于有很多表格…...

网络协议——Modbus-RTU
目录 1、简介 2、消息格式 3、Modbus寄存器种类说明 4、功能码01H 5、功能码02H 6、功能码03H 7、功能码04H 8、功能码05H 9、功能码06H 10、功能码0FH 11、功能码10H 1、简介 Modbus-RTU(Remote Terminal Unit)是一种串行通信协议࿰…...
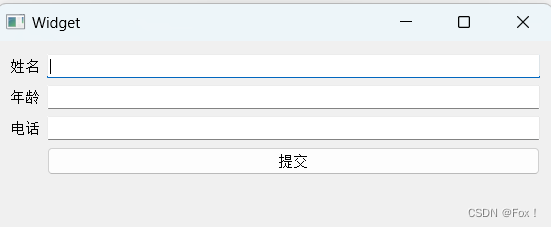
【Qt】如何优雅的进行界面布局
文章目录 1 :peach:写在前面:peach:2 :peach:垂直布局:peach:3 :peach:水平布局:peach:4 :peach:网格布局:peach:5 :peach:表单布局:peach: 1 🍑写在前面🍑 之前使⽤ Qt 在界⾯上创建的控件, 都是通过 “绝对定位” 的⽅式来设定的。也就是每个控件所在…...

【八股系列】分别说一下nodeJS和浏览器的事件循环机制?
文章目录 1. NodeJS1.1 Node.js 事件循环概念1.2 Node.js 事件循环工作流程1.3 Node.js 事件循环示例 2. 浏览器2.1 浏览器事件循环概念2.2 浏览器事件循环工作流程2.3 浏览器事件循环示例 1. NodeJS 1.1 Node.js 事件循环概念 在 Node.js 中,事件循环由 libuv 库…...
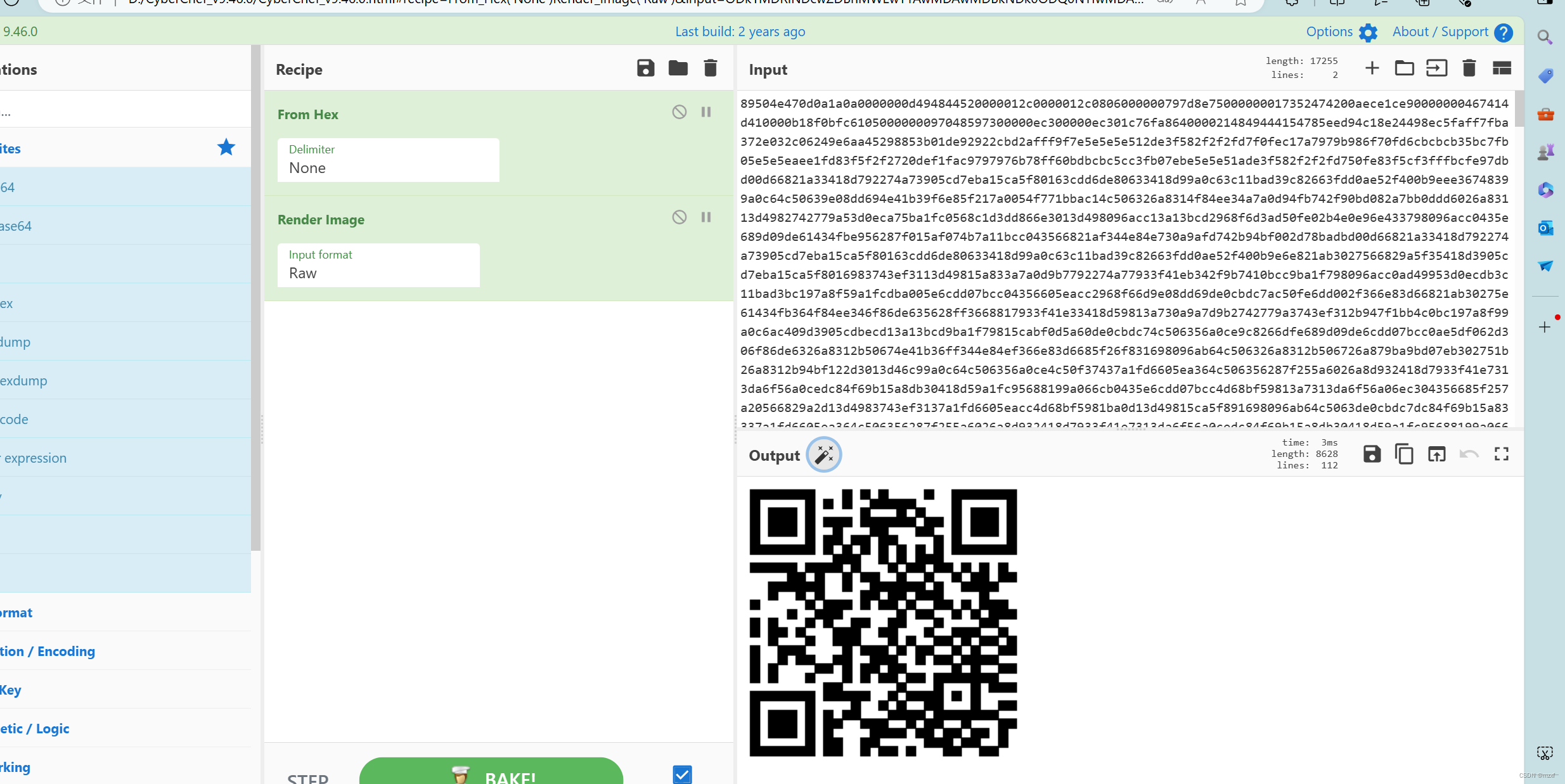
关于基础的流量分析(1)
1.对于流量分析基本认识 1)简介:网络流量分析是指捕捉网络中流动的数据包,并通过查看包内部数据以及进行相关的协议、流量分析、统计等来发现网络运行过程中出现的问题。 2)在我们平时的考核和CTF比赛中,基本每次都有…...

数据结构---树,二叉树的简单概念介绍、堆和堆排序
树 树的概念和结构 结构 在我们将堆之前,我们先来了解一下我们的树。 我们的堆是属于树里面的一种, 树是一种非线性结构,是一种一对多的一种结构,也就是我们的一个节点可能有多个后继节点,当然也可以只有一个或者没…...
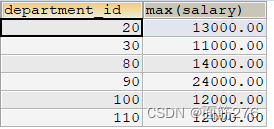
MySQL聚合函数(多行函数)
聚合函数(多行函数) 聚合函数作用于一组数据,并对一组数据返回一个值。 常见聚合函数 AVG和SUM函数 只作用于数值类型数据,不包含NULL 求工资平均值和总和 MIN和MAX函数 可以作用于任何数据类型(如字符串,…...

智慧教室课堂-专注度及考试作弊系统、课堂动态点名,情绪识别、表情识别和人脸识别结合
课堂专注度分析: 课堂专注度表情识别 作弊检测: 关键点计算方法 转头(probe)低头(peep)传递物品(passing) 侧面的传递物品识别 逻辑回归关键点 使用: 运行setup.py安装必要内容 python setup.py build develop 运行demo_inference.py 将…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...
