一阶数字高通滤波器
本文的主要内容包含一阶高通滤波器公式的推导和数字算法的实现以及编程和仿真
1 计算公式推导
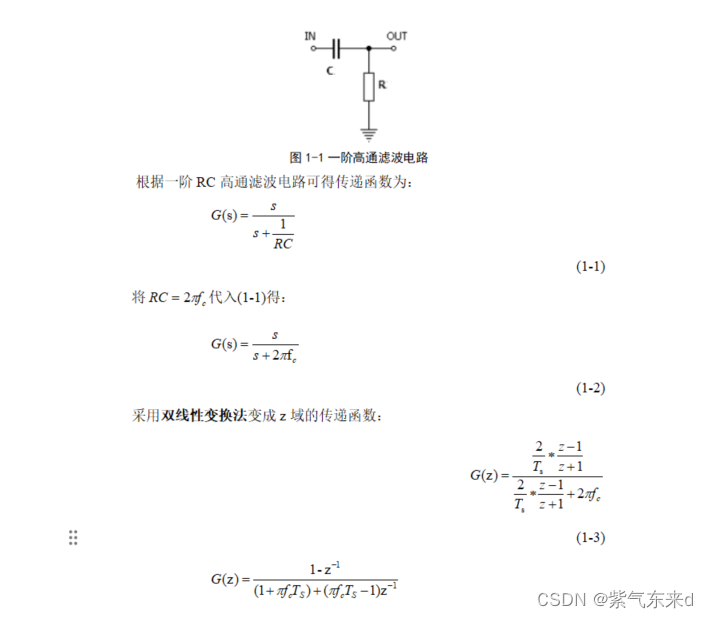

1.1.2 算法实现及仿真
利用python实现的代码如下:
import numpy as np
# from scipy.signal import butter, lfilter, freqz
import matplotlib.pyplot as plt
#2pifWc = 2*np.pi*30Tsw = 0.00314 #采样时间
halfdigiW=np.tan(Wc/2*Tsw )b10=1/(halfdigiW+1)
b11=-b10
a10=(1-halfdigiW)/(halfdigiW+1)x=np.linspace(-np.pi,np.pi,2000) #在[-pi,pi]区间上分割正2000个点 可以理解为信号采样时间为 2*pi/2000s
data=np.zeros_like(x) #输入信号 保存被干扰的信号
data1=np.zeros_like(x) #输入信号,保存未被干扰的信号,方便与滤波后的波形进行比较
y1=np.zeros_like(x) #一阶滤波输出
y2=np.zeros_like(x) #二阶滤波输出 陷波:对希望滤除的特定频率有很好的滤除作用
for i in range(len(x)):data[i] =np.sin( 2 * np.pi * x[i])+0.5*np.sin(30* 2 * np.pi * x[i]) #幅值为1频率为 1Hz的低频信号 + 幅值为0.5 频率为30hz的高频信号data1[i]=0.5*np.sin(130* 2 * np.pi * x[i])# y2[i] = b0*data[i]+b1*data[i-1]+a0*y2[i-1]y1[i] = b10 * data[i] + b11 * data[i - 1] + a10 * y1[i - 1]
y2[0] = 0
y2[1] = 0
y1[0] = 0
y1[1] = 0
#绘原始信号 + 滤波后的信号
plt.subplot(2, 1, 1)
plt.plot(x,data ,label='sig+noise')
plt.plot(x,y1, 'r',label='first order HP')#绘制理想信号 + 滤波后的信号
plt.subplot(2, 1, 2)
plt.plot(x,data1 ,label='sig')
plt.plot(x,y1, 'r',label='first order HP')
plt.grid()
plt.legend()
plt.show()以下是在python中仿真的波形图:

图1-2 fc=0.5Hz
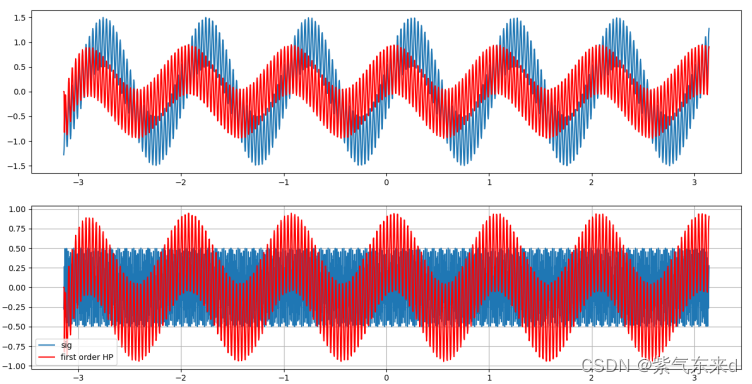
图1-3 fc=2Hz
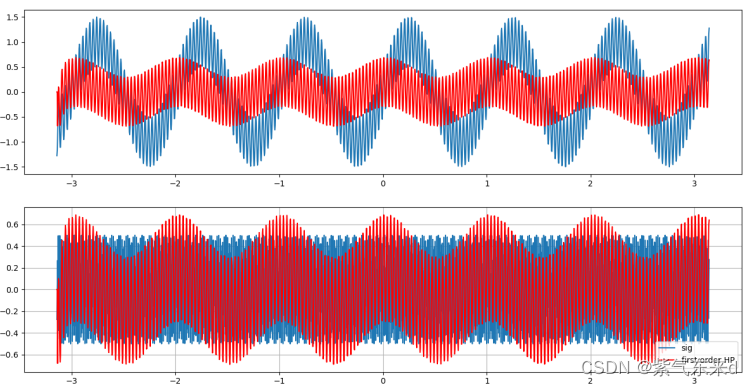
图1-4 fc=5Hz
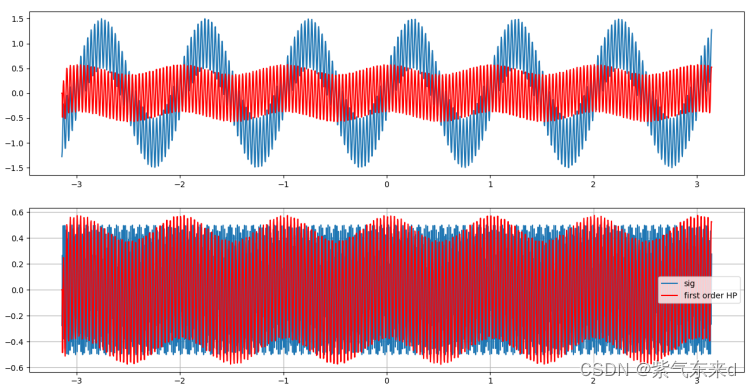
图1-5 fc=10Hz
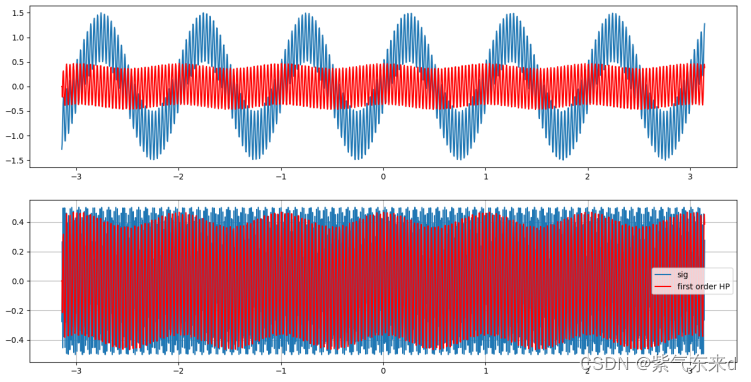
图1-6 fc=20Hz
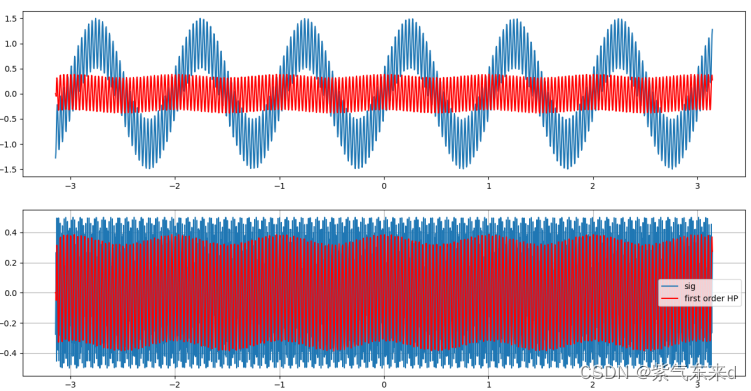
图1-7 fc=30Hz

图1-8 fc=40Hz
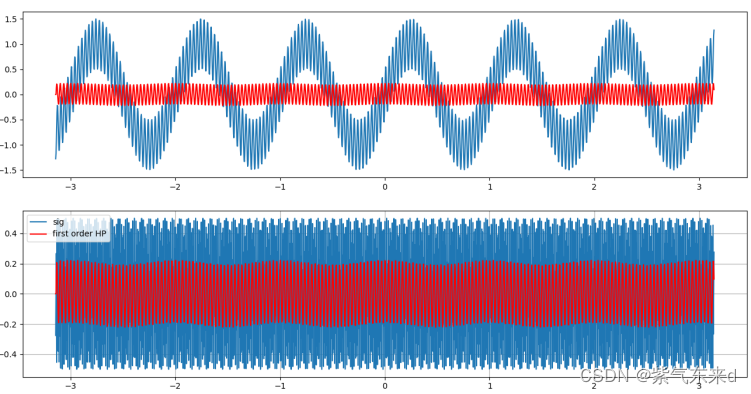
图1-9 fc=60Hz
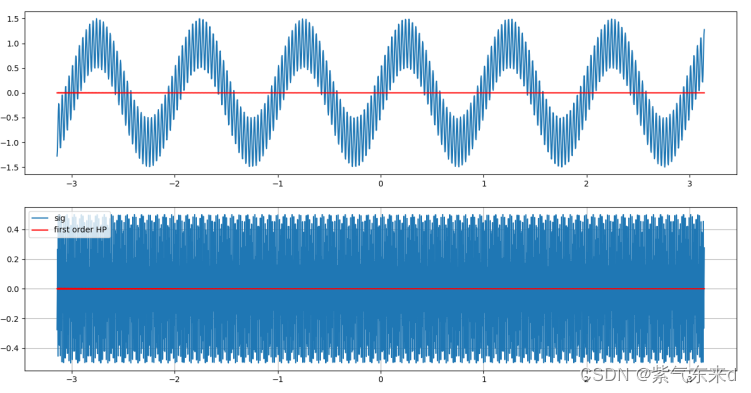
图1-10 fc=159Hz
输入的信号是幅值为1 频率为 1Hz的低频信号 加上 幅值为0.5 频率为30Hz的高频信号,采样时间为0.003s,从图1-2到图1-10的仿真波形可以看出,当fc为0.5Hz时,滤后的波形有微小的衰减作用,但几乎和原波形一致,当逐渐增大截止频率fc,对低频的滤除结果越来越强,高频越来越接近高频本身的波形,当截止频率高于高频频率时,高频本身也会被滤掉。当截止频率大于等于1/2采样频率时,输出的是一条直线。
利用C语言实现的代码如下:
#ifndef _MHPF1W_F_H_
#define _MHPF1W_F_H_#include <stdint.h>
struct MHpf1W_F
{/*初始化*/struct{void (*Set)(struct MHpf1W_F *self, float cutFreq, int samFreq); //设置截止和采样频率void (*VaryCutFreq)(struct MHpf1W_F *self, float cutFreq); //改变截止频率float cutFreq; //截止频率float samFreq; //采样频率} Init;/*采样计算*/struct{int (*In)(struct MHpf1W_F *self, int Xn);int out_y; //输出值} Prd;/*变量 中间变量 系数等,由初始参数 初始化计算得出*/struct{float Ts; //采样周期int a0, b0, b1; //差分系数int Xn_1, Yn_1;} pri;
};
void MHpf1W_F_Create(struct MHpf1W_F *self);
#endif
//创建方式
// struct MHpf1W_F mlp;
// MHpf1W_F_Create(&mlp);
// mlp.Init.Set(&mlp,2, 1000); fc=20Hz fs=1000Hz#include "MHpf1W_F.h"
#include <string.h>
#include "math.h"static const float PI = 3.1415926535897932384626f;
#define MID(a,min,max) (a= (a<min)?min:(a<max)?a:max)
#define Q15M(a,b) ((a*b)>>15)
/******************************************************************************** 函 数 名 : _Update* 函数功能 : 各系数计算,参数更新* 输入参数 : 滤波器对象 struct MHpf1W_F *self* 返 回 值 : 无*******************************************************************************/
static void _Update(struct MHpf1W_F *self)
{float halfdigiW,tgAnaWT ;halfdigiW = PI * self->Init.cutFreq * self->pri.Ts;tgAnaWT = tan(halfdigiW); //ignore the 1/Tself->pri.b0 = 1/(tgAnaWT+1)*32768; //转成Q15格式self->pri.b1 = -self->pri.b0; //转成Q15格式self->pri.a0 =((1-tgAnaWT)/(tgAnaWT+1))*32768; //转成Q15格式self->pri.Xn_1 = 0;self->pri.Yn_1 = 0;
}
/******************************************************************************** 函 数 名 : InitSet* 函数功能 : 初始化* 输入参数 : cutFreq----截至频率* samFreq----计算机采样频率* 返 回 值 : 无*******************************************************************************/
static void InitSet(struct MHpf1W_F *self, float cutFreq, int samFreq)
{self->Init.cutFreq = MID(cutFreq , 0.0f , samFreq*0.5f);; //截止频率self->Init.samFreq = samFreq; //采样频率self->pri.Ts = 1.0f / self->Init.samFreq; //采样周期 1/Ts_Update(self);
}
/******************************************************************************** 函 数 名 : InitVaryCutF* 函数功能 : 改变截止频率* 输入参数 : cutFreq----截至频率* 返 回 值 : 无*******************************************************************************/
static void InitVaryCutF(struct MHpf1W_F *self, float cutFreq)
{self->Init.cutFreq = cutFreq;_Update(self);
}
/******************************************************************************** 函 数 名 : PrdIn* 函数功能 : 本次输出结果计算* 输入参数 : Xn----本次输入值* 返 回 值 : 本次滤波后的值* 计算公式 :Y(n)=b0*X(n)+b1*X(n-1)+a0*Y(n-1)*******************************************************************************/
static int PrdIn(struct MHpf1W_F *self, int Xn)
{/*Y(n)=b0*X(n)+b1*X(n-1)+b2*X(n-2)+a0*Y(n-1)+a2*Y(n-2)*/self->Prd.out_y = Q15M(self->pri.b0 , Xn ) + \Q15M(self->pri.b1 , self->pri.Xn_1 ) + \Q15M(self->pri.a0 , self->pri.Yn_1 ) ;self->pri.Yn_1 = self->Prd.out_y;self->pri.Xn_1 = Xn;return self->Prd.out_y;
}
/******************************************************************************** 函 数 名 : MHpf1W_F_Create* 函数功能 : 创建对象 初始化* 输入参数 : self对象* 返 回 值 : 无*******************************************************************************/
void MHpf1W_F_Create(struct MHpf1W_F *self)
{memset(self, 0, sizeof(struct MHpf1W_F));self->Init.Set = InitSet;self->Init.VaryCutFreq = InitVaryCutF;self->Prd.In = PrdIn;
}单片机+匿名科创地面站的软件输出波形如下:
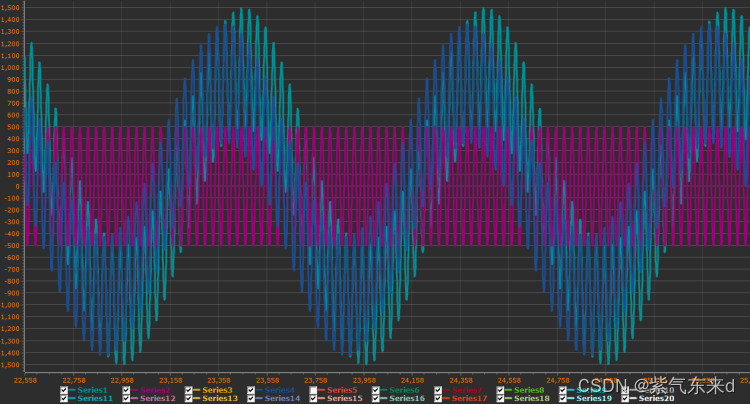
图1-11 fc=0.5Hz
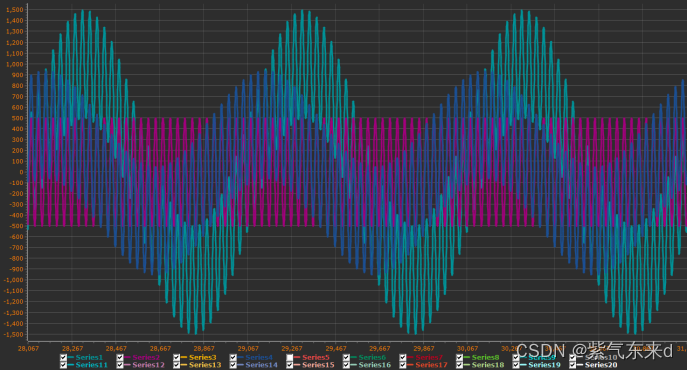
图4-12 fc=2Hz

图1-13 fc=5Hz
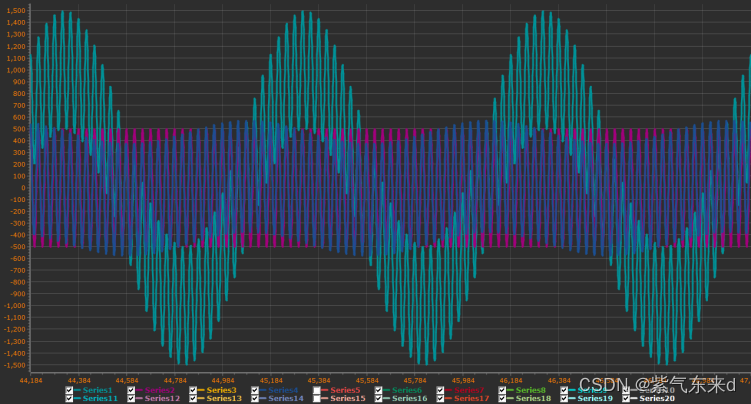
图1-14 fc=10Hz
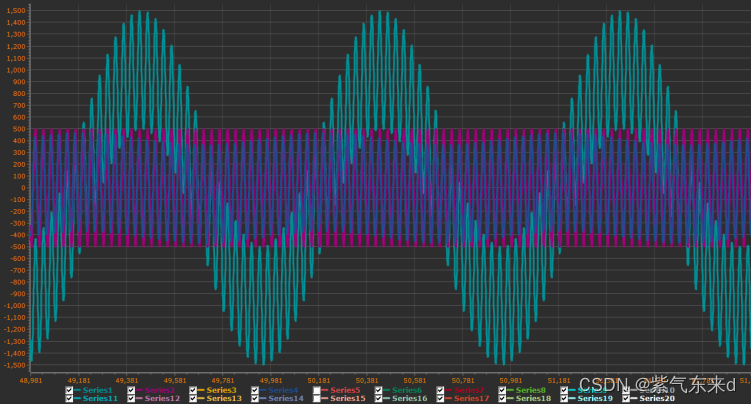
图1-15 fc=20Hz
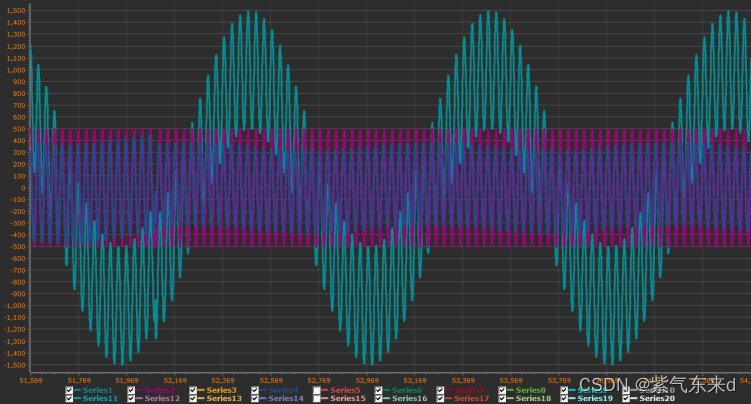
图1-16 fc=30Hz
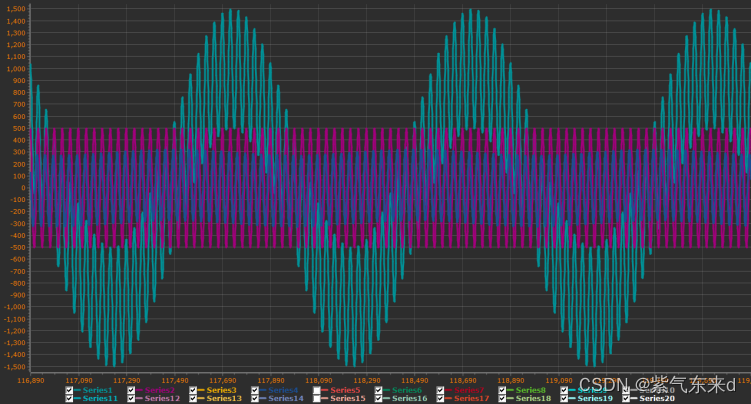
图1-17 fc=40Hz
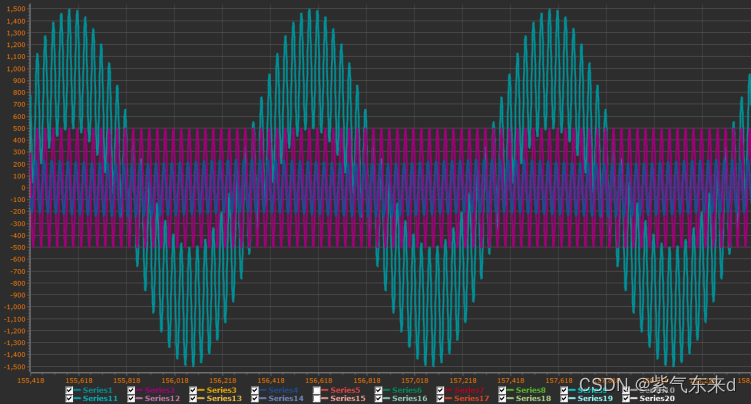
图1-18 fc=60Hz
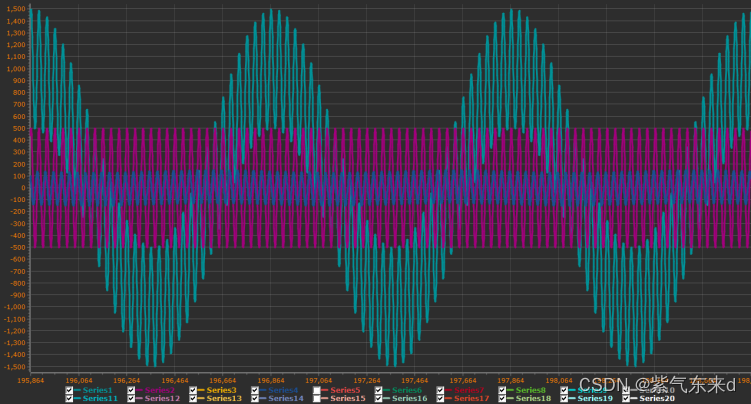
图1-18 fc=100Hz

图1-18 fc=200Hz
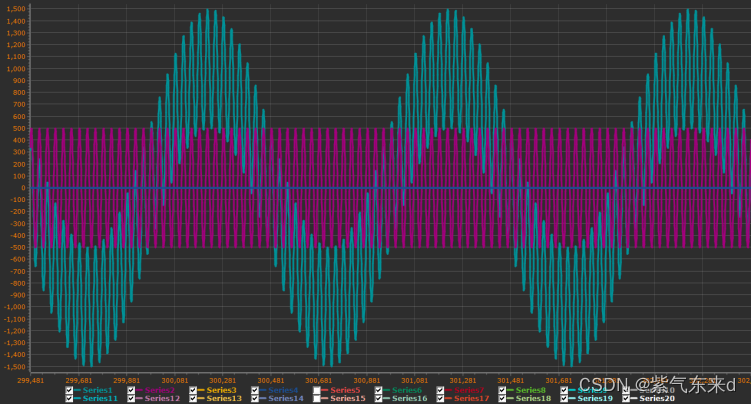
图1-18 fc=500Hz
单片机模拟输入的信号是幅值为1000 频率为 1Hz的低频信号加上幅值为500 频率为30Hz的高频信号,采样时间为0.001s,从图1-11到图1-18的波形可以看出,输出变化的规律现象和python仿真的规律和现象是一致的,同样当截止频率大于等于1/2采样频率时,输出的是一条直线。
相关文章:

一阶数字高通滤波器
本文的主要内容包含一阶高通滤波器公式的推导和数字算法的实现以及编程和仿真 1 计算公式推导 1.1.2 算法实现及仿真 利用python实现的代码如下: import numpy as np # from scipy.signal import butter, lfilter, freqz import matplotlib.pyplot as plt #2pifW…...
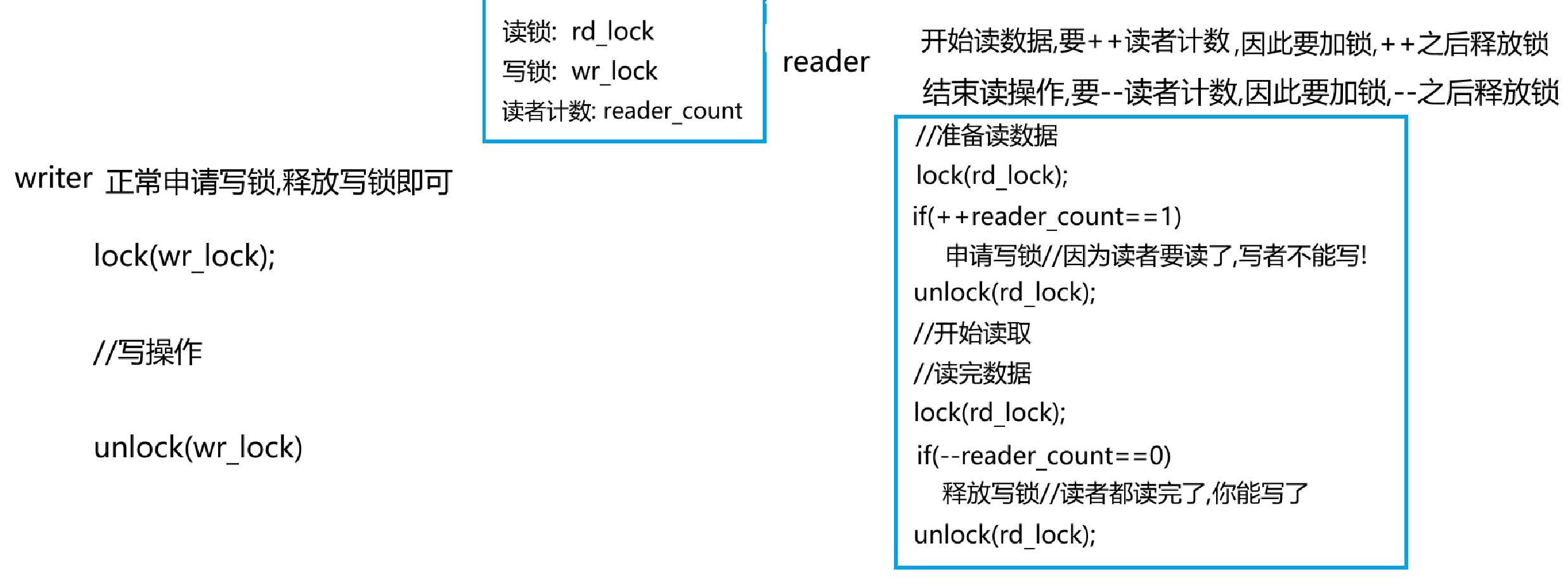
Linux多线程系列2: 模拟封装简易语言级线程库,线程互斥和锁,线程同步和条件变量,线程其他知识点
Linux多线程系列2: 模拟封装简易语言级线程库,线程互斥和互斥锁,线程同步和条件变量,线程其他知识点 1.前言 一.模拟C11线程库自己封装简易语言级线程库1.实现框架2.迅速把构造等等函数写完3.start和work1.尝试一2.尝试二3.最终版本4.给出代码 二.模拟实现多线程(为编写线程池做…...
VUE3-form表单保存附件与基本信息
element-ui代码 <el-dialog :title"上传附件" v-model"dialogAdds.visible" width"500px" append-to-body> <el-form-item label"唯一标识"> <dict-tag v-if"form.groupId" :options"unique_identifica…...

无线网络安全技术基础
无线网络安全技术基础 无线网络安全风险和隐患 随着无线网络技术广泛应用,其安全性越来越引起关注.无线网络的安全主要有访问控制和数据加密,访问控制保证机密数据只能由授权用户访问,而数据加密则要求发送的数据只能被授权用户所接受和使用。 无线网络在数据传输时以微波进…...

sheng的学习笔记-docker部署Greenplum
目录 docker安装gp数据库 mac版本 搭建gp数据库 连接数据库 windows版本 搭建gp数据库 连接数据库 docker安装gp数据库 mac版本 搭建gp数据库 打开终端,输入代码,查看版本 ocker search greenplum docker pull projectairws/greenplum docker…...

【投稿资讯】区块链会议CCF A -- SP 2025 截止6.6、11.14 附录用率
会议名称:46th IEEE Symposium on Security and Privacy( S&P) CCF等级:CCF A类学术会议 类别:网络与信息安全 录用率:2023年 195/1147,2024年录用了17篇和区块链相关的论文 Topics of interest inc…...

C++哪些函数不能被声明为虚函数
在C中,某些函数不能被声明为虚函数。下面详细解释哪些函数不能被声明为虚函数,并通过代码示例进行说明。 C哪些函数不能被声明为虚函数 不能声明为虚函数的函数示例代码及解释一、构造函数不能是虚函数二、静态成员函数不能是虚函数三、友元函数不能是虚…...

vue中数据已经改变了,但是table里面内容没更新渲染!
解决方案: 给table或者el-table标签上添加一个动态key值,只要数据发生改变,key值变动一下即可 标签上: :key“timeStamp” 初始data:timeStamp:0, 更新数据:this.timeStamp 这样每次更新数据ÿ…...

头歌实践教学平台:Junit实训入门篇
第2关:Junit注解 任务描述 给出一个带有注解的Junit代码及其代码打印输出,要求学员修改注解位置,让输出结果变为逆序。 相关知识 Junit注解 Java注解((Annotation)的使用方法是" 注解名" 。借助注解&a…...
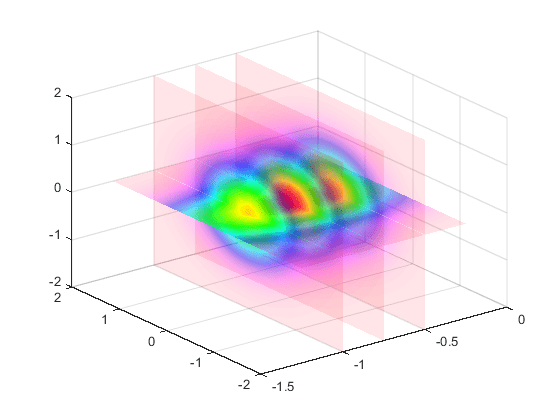
matlab使用教程(80)—修改图形对象的透明度
1.更改图像、填充或曲面的透明度 此示例说明如何修改图像、填充或曲面的透明度。 1.1坐标区框中所有对象的透明度 透明度值称为 alpha 值。使用 alpha 函数设置当前坐标区范围内所有图像、填充或曲面对象的透明度。指定一个介于 0(完全透明)和 1&#x…...

mysql bin 日志转成sql
首先确定mysql binlog 服务开启 SHOW VARIABLES LIKE log_bin; 找到binlog日志 find / -name mysql-bin.* -type f 下载下来 本地找到mysql安装位置的bin目录 在窗口路径处直接输入cmd 执行 mysqlbinlog --no-defaults --base64-outputdecode-rows -v --start-datetime&…...

河南道路与桥梁乙级资质申请:注册证书与职称证书准备
在河南道路与桥梁乙级资质申请中,注册证书与职称证书的准备是不可或缺的环节。以下是关于如何准备这些证书的一些关键步骤和要点: 明确所需证书类型: 注册证书:这通常指的是相关专业的注册工程师证书,如注册土木工程师…...

3D工业视觉
前言 本文主要介绍3D视觉技术、工业领域的应用、市场格局等,主要技术包括激光三角测量、结构光、ToF、立体视觉。 一、核心内容 3D视觉技术满足工业领域更高精度、更高速度、更柔性化的需求,扩大工业自动化的场景。 2D视觉技术基于物体平面轮廓&#…...

使用auth_basic模块进行基础认证
在建立和维护Web服务器时,身份认证是一个至关重要的环节。Nginx作为一个高性能的Web服务器,支持许多认证方法,其中较为简单和常用的一种即是基础身份认证(Basic Authentication),这需要借助auth_basic模块实…...
深度解析物联网平台:优化数据点位管理的实战策略
策略管理 策略,作为在物联网平台数据点位创建过程中可设定的规则,涵盖了多个重要方面,策略是在创建点位的时候,可以设置的规则,包括存储策略、告警策略、通知策略以及联动策略。这些策略都是通过专门的列表页面进行集…...

Spring常见问题
如何理解spring属于低侵入式设计? 在代码中不需要写明具体依赖对象,在运行时进行自动注入,降低了组件的耦合依赖的是接口,而接口的实现类具有拓展性 Spring IOC 实现了什么功能,谈谈你对IOC的理解。 负责创建对象&…...
MiniMax Golang2轮面试,期望薪资25K
一面 1、自我介绍 2、简单介绍一下你们成立了这个finance的财务中台之后,整体的服务架构是怎么样的吗? 3、就你提到的预算池项目,展开说说背景,以及解决了怎么样的问题? 4、为什么采用针对T-1订单的异步计算方案&a…...

MyBatis系统学习篇 - MyBatis的缓存
MyBatis的缓存实现原理主要基于三级缓存机制,包括一级缓存(本地缓存)、二级缓存(全局缓存)和三级缓存(跨会话缓存)。这个缓存在我们实际开发中可以避免我们查询重复的数据,在一定程度…...
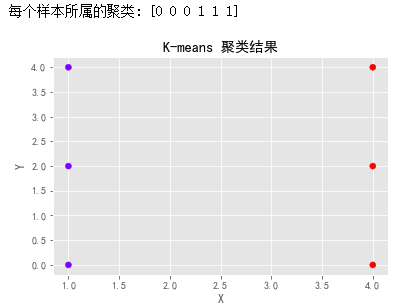
K-means聚类模型
目录 1.定义 2.K-means聚类模型的优点 3.K-means聚类模型的缺点 4.K-means聚类模型的应用场景 5.对K-means聚类模型未来的展望 6.小结 1.定义 什么是 K-means 聚类模型?K-means 聚类模型是一种无监督学习算法,用于将数据划分为不同的组或簇&#…...

免费分享一套微信小程序旅游推荐(智慧旅游)系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】,帅呆了~~
大家好,我是java1234_小锋老师,看到一个不错的微信小程序旅游推荐(智慧旅游)系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序旅游推荐(智慧旅游)系统(SpringBoot后端Vue管理端) Java毕业设计…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...
