回溯法——(2)n皇后问题(C语言讲解)(LeetCode51 N皇后思想)(4皇后棋盘画图举例)(附代码)
目录
一、问题概括
二、算法分析
三、举例(4皇后棋盘)
四、算法实现
4.1运行结果:
51. N 皇后 - 力扣(LeetCode)
一、问题概括
n皇后问题是19世纪著名数学家高斯于1850年提出的。
问题是:在n×n的棋盘上摆放n个皇后,使其不能相互攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
二、算法分析
按照国际象棋规则,皇后可以攻击与之在同一行或同一列或同一斜线上的棋子。
核心分析:
n后问题等价于在n×n格的棋盘上放置n个皇后,任何2个皇后不放在同一行或同一列或同一斜线上。
由以上问题与分析可知,棋盘每一行可以并且必须拜访1个皇后。
1、那么n皇后问题的可能解用1个n元向量(x1,x2,......,xn)表示,即第i个皇后摆放在第i行第xi列的位置(1≤i≤n且1≤xi≤n)。
2、由于两个皇后不能位于同一列,所以,n皇后问题的解的向量必须满足约束条件xi≠xj。
3、不在同一斜线上的约束条件|i-j|≠|xi-xj|。
三、举例(4皇后棋盘)
下面将利用4皇后问题详细讲解。
(Q代表皇后放置符号,×代表放置失败的符号)
①首先把皇后1摆放到所在第一行第一列。

②皇后2本着不能与皇后1同行同列同斜线的原则 ,经过不懈努力尝试最终放置在了第二行第三列。

③皇后3根据同样的原理(同行同列同斜线的原则)尝试了第三行的任何一列都冲突。

④因此进行回溯,将皇后2摆放到下一个位置, 即皇后2第二行第四列。
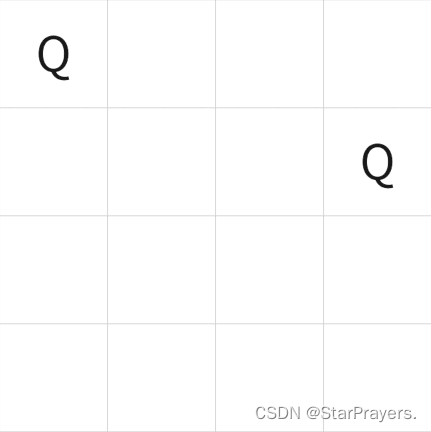
⑤皇后3再次本着同行同列同斜线的原则,摆放到第三行第二列。

⑥
1、皇后4,摆放到第四行任何一列,都会违背同行同列同斜线的原则,进行回溯;
2、发现皇后3除了摆放到第三行第二列不违背原则,其他列放置同样违背原则,因此我们继续回溯;
3、但当我们此时回溯到皇后2时发现皇后2已经位于相应行最后一列了,所以我们只能继续回溯;
4、回溯到皇后1,将皇后1摆放到第一行第二列。

⑦接下来,将皇后2摆放到第二行第四列,皇后3摆放到第三行第一列,皇后4摆放到第四行第三列的位置,便得到了4皇后问题的一个解。

四、算法实现
#include <stdio.h>
#include <stdlib.h>#define N 4 // 可以更改 N 的值来解决不同大小的皇后问题
int count = 0;void printBoard(int board[N][N]);// 函数来检查是否可以在 board[row][col] 放置皇后
int isSafe(int board[N][N], int row, int col) {int i, j;// 检查同一列for (i = 0; i < row; i++)if (board[i][col] == 1)return 0;// 检查左上对角线for (i = row, j = col; i >= 0 && j >= 0; i--, j--)if (board[i][j] == 1)return 0;// 检查右上对角线for (i = row, j = col; i >= 0 && j < N; i--, j++)if (board[i][j] == 1)return 0;return 1;
}// 函数来解决 N 皇后问题
void solveNQUtil(int board[N][N], int row, int& solutions) {// 如果所有皇后都放置完成if (row >= N) {solutions++;printBoard(board);return;}// 在当前行尝试放置皇后并递归地放置剩下的皇后for (int col = 0; col < N; col++) {// 检查放置皇后的位置是否安全if (isSafe(board, row, col)) {board[row][col] = 1; // 放置皇后solveNQUtil(board, row + 1, solutions); // 递归放置下一个皇后board[row][col] = 0; // 回溯}}
}// 打印棋盘函数
void printBoard(int board[N][N]) {printf("Solution %d:\n", ++count);for (int i = 0; i < N; i++) {for (int j = 0; j < N; j++)printf("%d ", board[i][j]);printf("\n");}printf("\n");
}// 用于解决 N 皇后问题的主函数
void solveNQ() {int board[N][N] = { 0 }; // 初始化棋盘int solutions = 0;solveNQUtil(board, 0, solutions);printf("Total number of solutions are %d\n", solutions);
}// 主函数
int main() {solveNQ();return 0;
}4.1运行结果:
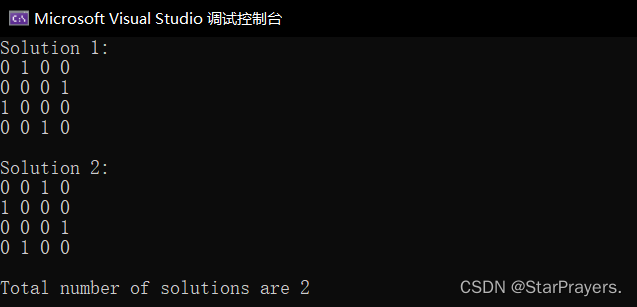
这个代码尝试在棋盘的每一行放置皇后,并使用递归来检查每个位置是否安全。如果找到一个安全的放置位置,就会递归地尝试下一行。这个过程一直重复,直到所有皇后都被放置在棋盘上。每次成功放置所有皇后时,它都会增加解决方案的数量,并打印出当前棋盘作为一个新的解决方案。
相关文章:

回溯法——(2)n皇后问题(C语言讲解)(LeetCode51 N皇后思想)(4皇后棋盘画图举例)(附代码)
目录 一、问题概括 二、算法分析 三、举例(4皇后棋盘) 四、算法实现 4.1运行结果: 51. N 皇后 - 力扣(LeetCode) 一、问题概括 n皇后问题是19世纪著名数学家高斯于1850年提出的。 问题是:在nn的棋盘上…...

数据库系统概论(第5版)复习笔记
笔记的Github仓库地址 👆这是笔记的gihub仓库,内容是PDF格式。 因为图片和代码块太多,放到CSDN太麻烦了(比较懒🤣) 如果感觉对各位有帮助的话欢迎点一个⭐\^o^/...

数仓领域,Serving 是什么概念?
在数据仓库(Data Warehouse)和更广泛的数据工程领域中,“Serving”通常指的是将处理和优化后的数据提供给最终用户或应用程序的过程。这包括数据的查询、检索、展示等操作,使得数据能够在决策支持、报告、分析、或机器学习等应用中…...

Python筑基之旅-MySQL数据库(三)
目录 一、数据库操作 1、创建 1-1、用mysql-connector-python库 1-2、用PyMySQL库 1-3、用PeeWee库 1-4、用SQLAlchemy库 2、删除 2-1、用mysql-connector-python库 2-2、用PyMySQL库 2-3、用PeeWee库 2-4、用SQLAlchemy库 二、数据表操作 1、创建 1-1、用mysql-…...
(全面)Nginx格式化插件,Nginx生产工具,Nginx常用命令
目录 🎫 前言 🎉 开篇福利 🎁 开篇福利 x2 Double happiness # 介绍 # 地址 # 下载 💻 命令及解析 # 整个文件系统中搜索名为nginx.conf的文件 # 编辑nginx.conf文件 # 重新加载配置文件 # 快速查找nginx.conf文件并使…...

软考 软件设计师 场景分析题 速成篇
文章目录 试题一:数据流图💖 基本图形元素1. 外部实体2. 数据存储3. 加工4. 数据流 📚 例题(1)实体名称(2)数据存储名称(3)数据流① 父子图平衡② 加工有输入有输出④ 数…...
防止SQL注入、XSS攻击和文件上传漏洞)
[学习笔记](Python3)防止SQL注入、XSS攻击和文件上传漏洞
学习笔记:防止SQL注入、XSS攻击和文件上传漏洞(Python3) 本笔记由生成式大模型GPT-4o自动整理。注意AI可能犯错。代码和理论由GPT-4o(2024-5-21)自行撰写未经人工复核。 参数化查询防SQL注入 参数化查询通过将SQL语句和数据分离来防止SQL注…...
西门子CPU与汇川伺服通信与控制
西门子CPU与汇川620F伺服通信与控制 一、西门子CPU与汇川620F伺服通信与控制1、器件准备2、伺服软件设置3、PLC添加汇川伺服描述文件4、PLC编程调试5、总结 二、西门子s7-1500限位信号接到伺服的方法1、通过默认报文获取限位信号2、添加自定义报文获取限位信号3、总结 三、西门…...
移动硬盘无法读取怎么修复?简单八步,轻松搞定!
移动硬盘在日常生活和工作中扮演着重要的角色,但有时我们可能会遇到移动硬盘无法读取的问题。这种情况可能导致数据无法访问,给用户带来一定的困扰。本文将介绍移动硬盘无法读取的可能原因以及针对这些问题的修复方法。 1. 检查硬件连接 当发现移动硬盘…...
c4d云渲染是工程文件会暴露吗?
在数字创意产业飞速发展的今天,C4D云渲染因其高效便捷而备受欢迎。然而,随着技术应用的深入,人们开始关注一个核心问题:在享受云渲染带来的便利的同时,C4D工程文件安全吗?是否会有暴露的风险?下…...

C语言/数据结构——每日一题(有效的括号)
一.前言 如果想要使用C语言来解决这道题——有效的括号:https://leetcode.cn/problems/valid-parentheses/description/我们必须要借用上一篇我们所讲的内容——栈的实现:https://blog.csdn.net/yiqingaa/article/details/138923750?spm1001.2014.3001.…...
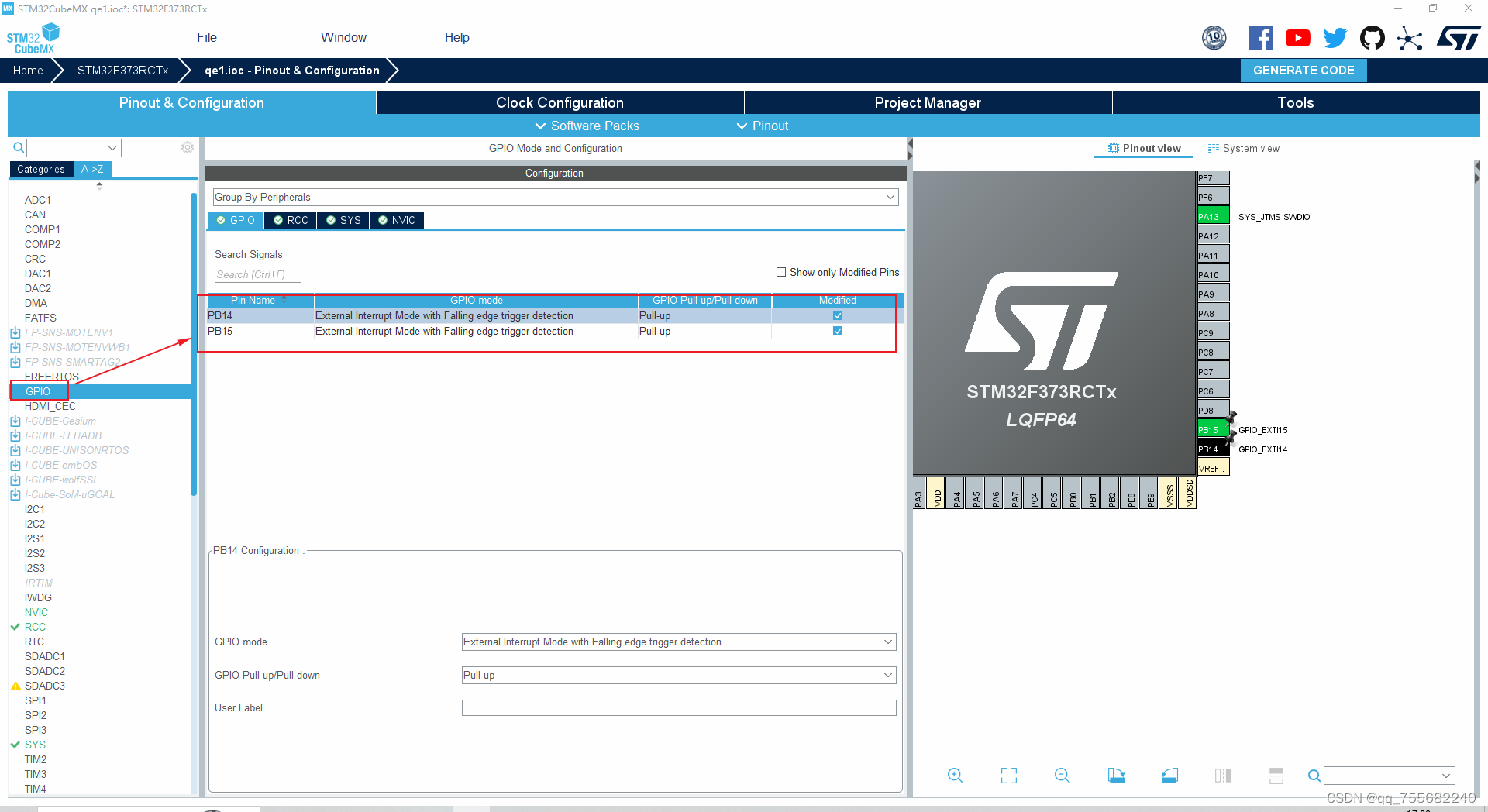
STM32使用旋转编码开关
一、旋转编码开关如何工作 编码器内部有一个开槽圆盘,连接到公共接地引脚 C。它还具有两个接触针 A 和 B,如下所示。 当您转动旋钮时,A 和 B 按照特定顺序与公共接地引脚 C 接触,具体顺序取决于转动旋钮的方向。 当它们与公共地接…...

OneMO同行 心级服务:中移物联OneMO模组助力客户终端寒冷环境下的稳定运行
中移物联OneMO模组以客户为中心,基于中国移动心级服务要求,开展“OneMO同行 心级服务 标定一流”高标服务主题活动,升级“服务内容““服务方式”和“服务意识”,为行业客户提供全新的服务体验。 近日,某车载监控设备…...

爬虫视图展示之 Power BI
实现方式 读取数据的实现 selenium 库 requests 库 存储媒介 MysqlElasticSearch 图表展示 GrafanaPower BI 是什么? Power BI 简单且快速,能够从 Excel 电子表格或本地数据库创建快速见解。 同时 Power BI 也可进行丰富的建模和实时分析ÿ…...

微软刚发布的Copilot+PC为什么让Intel和AMD尴尬?2024 AI PC元年——产业布局及前景展望
美国东部时间5月20日在微软位于华盛顿的新园区举行的发布会上,宣布将旗下AI助手Copilot全面融入Windows系统,能够在不调用云数据中心的情况下处理更多人工智能任务。 “将世界作为一个提示词就从Windows系统开始”。微软的新PC将是“CopilotPC”…...
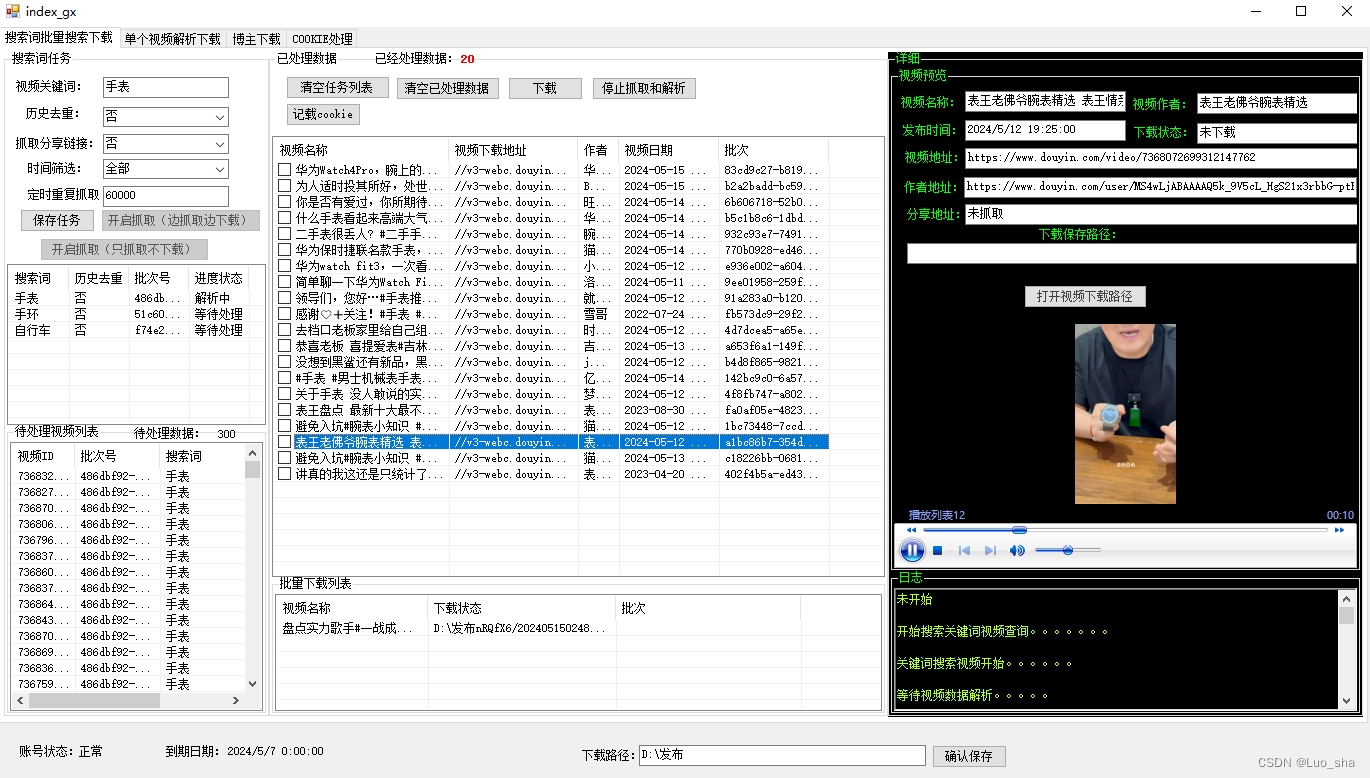
抖音视频怎么去水印保存部分源码|短视频爬虫提取收集下载工具
抖音视频怎么去水印保存部分源码|短视频爬虫提取收集下载工具 抖音视频去水印保存部分源码: 通过使用Python中的requests、re和os等库,可以编写如下代码来实现抖音视频去水印保存的功能。 短视频爬虫提取手机下载工具的使用方法: 该工具主…...
类的组合、作用域与可见性、类的静态成员、单例模式、
类的组合 一个类内嵌其他类的对象作为成员的情况 has - a组合 初始化列表的另一用途:为了调用数据成员的带参构造函数 能够层层递进 class Line { public:Line(int x1 0, int y1 0, int x2 0, int y2 0);Line(const Line &other);~Line();Line(const Po…...

高速公路定向广播(声光一体) HT-600D
1、产品概述: HT-600D声光一体平面波IP定向广播是北京恒星科通创新性研发产品,采用公司自主研发的平面波传声技术,该产品具有高声压、强指向性、高清晰度等特点,采用定向声传声技术将声音聚集到正前方定向传输,周边声压级明显降低…...

2024离婚新规已生效,不用等30天冷静期,线上开庭
2024年离婚必知的12条法律知识: ✅分居多久都不会自动离婚,想离婚,必需通过协议或起诉程序离婚 ✅婚后的工资收入,继承的遗产(未指定只给一人)都是夫妻共同财产 ✅没有领结婚证,或领证后没有共同生活&#…...

从零搭建python环境:深入解析虚拟环境与Python版本管理
新书上架~👇全国包邮奥~ python实用小工具开发教程http://pythontoolsteach.com/3 欢迎关注我👆,收藏下次不迷路┗|`O′|┛ 嗷~~ 目录 一、引言:为何需要虚拟环境? 二、虚拟环境的创建与命名 1. 虚拟环境…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...
