day15|各种遍历的应用
相关题目:
层次遍历会一打十
反转二叉树
对称二叉树
层次遍历会一打十
自底向上的层序遍历

实现思路:层次遍历二叉树,将遍历后的结果revers即可
public List<List<Integer>> levelOrderBottom(TreeNode root) {List<List<Integer>> res = new ArrayList<>();Queue<TreeNode> que = new ArrayDeque<>();if (root == null) {return res;}que.offer(root);int size = 0;while (!que.isEmpty()) {size = que.size();List<Integer> list = new ArrayList<>();while (size > 0) {TreeNode cur = que.poll();list.add(cur.val);if (cur.left != null) {que.offer(cur.left);}if (cur.right != null) {que.offer(cur.right);}size--;}res.add(list);}Collections.reverse(res);return res;}
输出二叉树的右视图节点
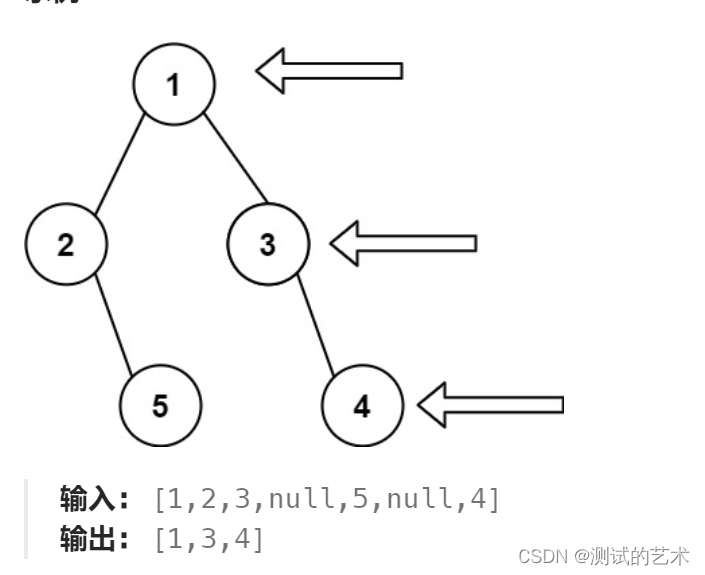
实现思路:层次遍历二叉树,记录二叉树每一层的节点数,到达该层最后一个节点时,将其加入到结果集即可
public List<Integer> rightSideView(TreeNode root) {List<Integer> res = new ArrayList<>();if(root == null){return res;}Queue<TreeNode> que = new ArrayDeque<>();que.offer(root);int size = 0;while(!que.isEmpty()){size = que.size();while(size>0){TreeNode cur = que.poll();//遍历到该层最后一个节点if(size == 1){res.add(cur.val);}if(cur.left!=null){que.offer(cur.left);}if(cur.right!=null){que.offer(cur.right);}size--;}}return res;}
二叉树每层的平均值

实现思路:层次遍历二叉树,计算每一层的平均值,注意:每层数之和及平均值的数据类型
public List<Double> averageOfLevels(TreeNode root) {List<Double> res = new ArrayList<>();Queue<TreeNode> que = new ArrayDeque<>();if(root == null){return res;}int size = 0;que.offer(root);while(!que.isEmpty()){size = que.size();double sum = 0;for (int i = 0; i < size; i++) {TreeNode cur = que.poll();sum += cur.val;if(cur.left!=null){que.offer(cur.left);}if(cur.right!=null){que.offer(cur.right);}}res.add(sum/size);}return res;}
N叉树的·层次遍历
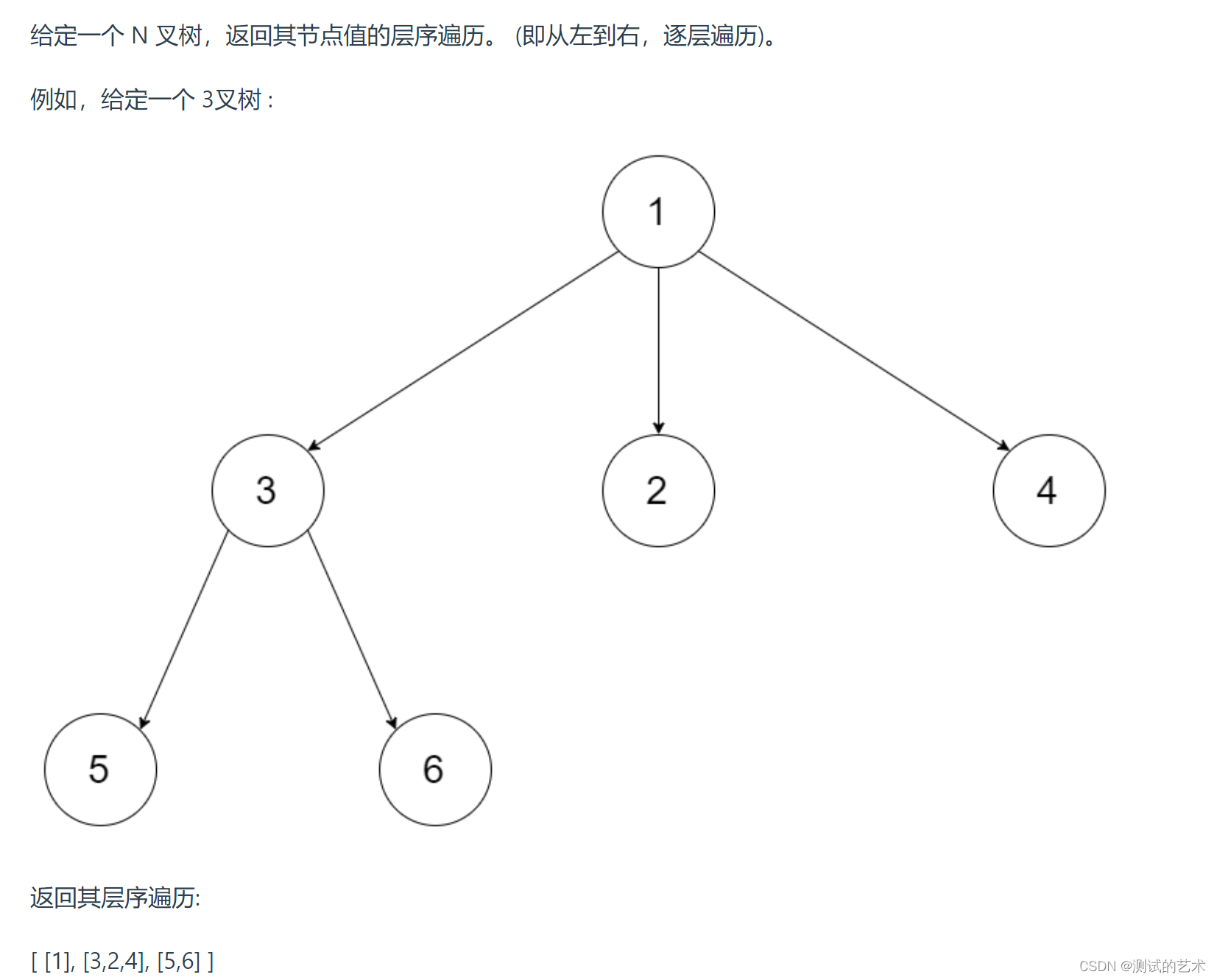
class Node {public int val;public List<Node> children;public Node() {}public Node(int _val) {val = _val;}public Node(int _val, List<Node> _children) {val = _val;children = _children;}
};public class LevelOrderNode {public List<List<Integer>> levelOrder(Node root) {List<List<Integer>> res = new ArrayList<>();if (root == null) {return res;}Queue<Node> que = new ArrayDeque<>();que.offer(root);while (!que.isEmpty()) {int size = que.size();List<Integer> list = new ArrayList<>();for (int i = 0; i < size; i++) {Node cur = que.poll();list.add(cur.val);List<Node> children = cur.children;if (children == null || children.size() == 0) {continue;}for (Node child : children) {if (child != null) {que.offer(child);}}}res.add(list);}return res;}}
在二叉树的每一行中找最大值
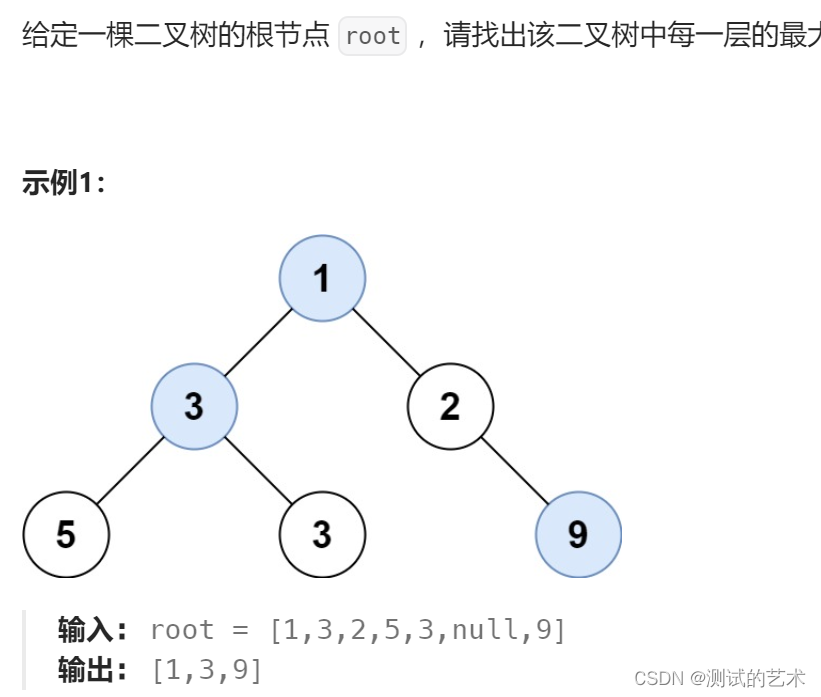
实现思路:层次遍历二叉树,记录每一层的最大值
public List<Integer> largestValues(TreeNode root) {List<Integer> res = new ArrayList<>();if(root == null){return res;}Queue<TreeNode> que = new ArrayDeque<>();int size = 0;que.offer(root);while(!que.isEmpty()){size = que.size();int max = Integer.MIN_VALUE;while(size>0) {TreeNode cur = que.poll();max = Math.max(max,cur.val);if(cur.left!=null){que.offer(cur.left);}if(cur.right!=null){que.offer(cur.right);}size--;}res.add(max);}return res;}
填充每个节点的下一个右侧节点指针
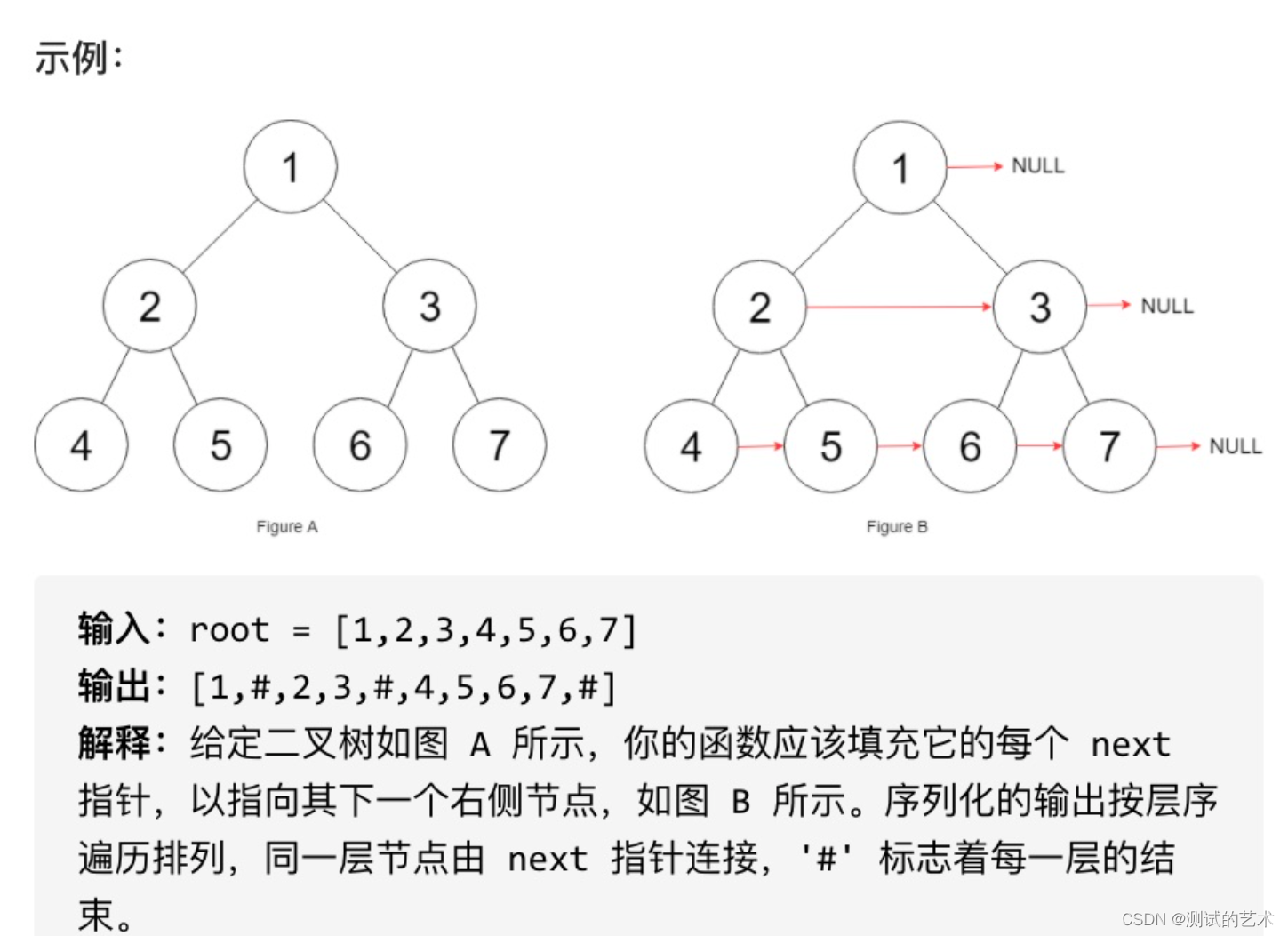
实现思路:层次遍历二叉树,记录每层元素个数,遍历每层元素,元素个数大于1时,使其next指针指向队头元素;元素个数为1时,使其next指针指向null即可
class NodeText {public int val;public NodeText left;public NodeText right;public NodeText next;public NodeText() {}public NodeText(int _val) {val = _val;}public NodeText(int _val, NodeText _left, NodeText _right, NodeText _next) {val = _val;left = _left;right = _right;next = _next;}
};
public class Connect {public NodeText connect(NodeText root) {Queue<NodeText> que = new ArrayDeque<>();if(root == null){return root;}que.offer(root);while(!que.isEmpty()){int size = que.size();while(size>0){NodeText cur = que.poll();if(size>1){NodeText temp = que.peek();cur.next = temp;}else{cur.next =null;}if(cur.left!=null){que.offer(cur.left);}if(cur.right!=null){que.offer(cur.right);}size--;}}return root;}
}
求二叉树的最大深度

实现思路:层次遍历二叉树,记录树的层数
public int maxDepth(TreeNode root) {int maxDepth = 0;int size = 0;if(root == null){return 0;}Queue<TreeNode> que = new ArrayDeque<>();que.offer(root);while(!que.isEmpty()){maxDepth++;size = que.size();while(size>0){TreeNode cur = que.poll();if(cur.left!=null){que.offer(cur.left);}if(cur.right!=null){que.offer(cur.right);}size--;}}return maxDepth;}
求二叉树的最小深度
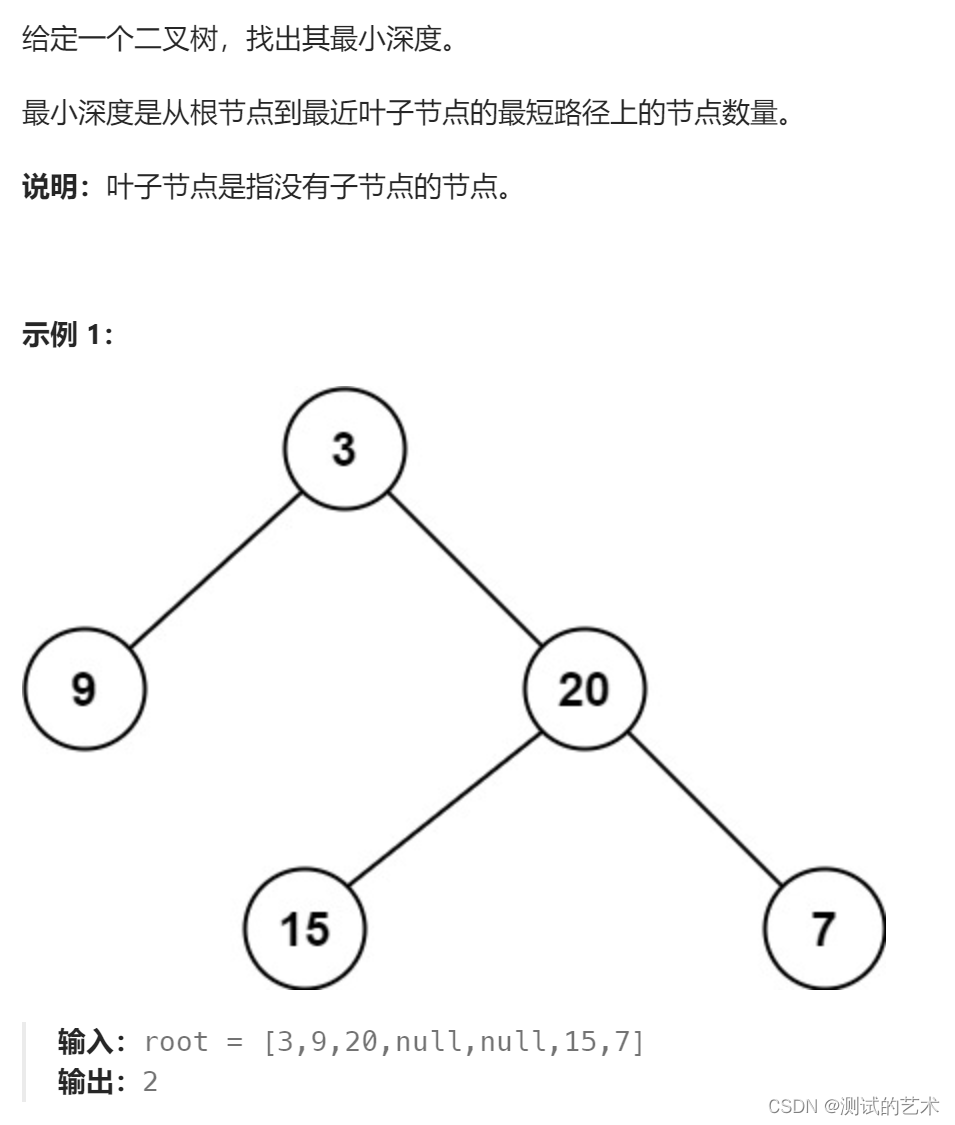
实现思路:层次遍历二叉树,当某个节点的左右孩子均为null时,输出该节点所在层数,及就是树的最小深度
public int minDepth(TreeNode root) {if (root == null) {return 0;}int deep = 0;int size = 0;Queue<TreeNode> que = new ArrayDeque<>();que.offer(root);while (!que.isEmpty()) {deep++;size = que.size();while (size > 0) {TreeNode cur = que.poll();if (cur.left == null && cur.right == null) {return deep;} else {if (cur.left != null) {que.offer(cur.left);}if (cur.right != null) {que.offer(cur.right);}}size--;}}return deep;}
反转二叉树(掌握递归遍历)
实现方法:使用前序遍历、后序遍历及其层次遍历均可实现
前序遍历实现方法:遍历中间节点,中间节点的左右孩子交换位置即可
后序遍历实现方法:遍历的左子树和右子树,交换中间节点左右孩子交换位置即可
层次遍历:遍历每一层的各个节点,反转各个节点的左右孩子即可
public class InvertTree extends TreeNode {public TreeNode invertTree(TreeNode root) {if(root == null){return null;}
// //前序
// swap(root);
// invertTree(root.left);
// invertTree(root.right);// //后序
// invertTree(root.left);
// invertTree(root.right);
// swap(root);//层次遍历--迭代Queue<TreeNode> que = new ArrayDeque<>();int size = 0;que.offer(root);while(!que.isEmpty()){size = que.size();while(size>0){TreeNode cur = que.poll();swap(cur);if(cur.left!=null){que.offer(cur.left);}if(cur.right!=null){que.offer(cur.right);}size--;}}return root;}public void swap(TreeNode root){TreeNode temp = root.left;root.left = root.right;root.right = temp;}
}
对称二叉树
递归实现:
递归三部曲
- 确定递归函数的参数和返回值
因为我们要比较的是根节点的两个子树是否是相互翻转的,进而判断这个树是不是对称树,所以要比较的是两个树,参数自然也是左子树节点和右子树节点。
返回值自然是bool类型。
代码如下:
bool compare(TreeNode* left, TreeNode* right) - 确定终止条件
要比较两个节点数值相不相同,首先要把两个节点为空的情况弄清楚!否则后面比较数值的时候就会操作空指针了。
节点为空的情况有:(注意我们比较的其实不是左孩子和右孩子,所以如下我称之为左节点右节点)
- 左节点为空,右节点不为空,不对称,return false
- 左不为空,右为空,不对称 return false
- 左右都为空,对称,返回true
- 左右都不为空,比较节点数值,不相同就return false
代码如下:
if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
else if (left->val != right->val) return false; // 注意这里我没有使用else
注意上面最后一种情况,我没有使用else,而是else if, 因为我们把以上情况都排除之后,剩下的就是 左右节点都不为空,且数值相同的情况。
3. 确定单层递归的逻辑
此时才进入单层递归的逻辑,单层递归的逻辑就是处理 左右节点都不为空,且数值相同的情况。
- 比较二叉树外侧是否对称 :传入的是左节点的左孩子,右节点的右孩子。
- 比较内侧是否对称:传入左节点的右孩子,右节点的左孩子。
如果左右都对称就返回true ,有一侧不对称就返回false 。
实现过程:
class Solution {public boolean isSymmetric(TreeNode root) {if (root == null) {return true;}return compare(root.left,root.right);}//递归实现public boolean compare(TreeNode left, TreeNode right) {if (left == null && right != null) return false;else if (left != null && right == null) return false;else if (left != null && right != null && left.val != right.val) return false;else if (left == null && right == null) return true;boolean inside = compare(left.left, right.right);boolean outside = compare(left.right, right.left);return inside && outside;}
}
相关文章:

day15|各种遍历的应用
相关题目: 层次遍历会一打十 反转二叉树 对称二叉树 层次遍历会一打十 自底向上的层序遍历 实现思路:层次遍历二叉树,将遍历后的结果revers即可 public List<List<Integer>> levelOrderBottom(TreeNode root) {List<List&l…...

第12周作业--HLS入门
目录 一、HLS入门 二、HLS入门程序编程 创建项目 1、点击Vivado HLS 中的Create New Project 2、设置项目名 3、加入文件 4、仿真 3、综合 一、HLS入门 1. HLS是什么?与VHDL/Verilog编程技术有什么关系? HLS(High-Level Synthesis,…...

WorkManager使用技巧及各Android版本适配
WorkManager使用技巧及各Android版本适配 WorkManager是Android Jetpack中用于处理异步任务的库,它能够保证任务即使在应用关闭或设备重启后也能被执行。以下是WorkManager的使用技巧和代码示例,以及不同Android版本的适配方法。 1. 初始化WorkManager…...

鼠标滚轮使用时上下跳动的解决方法
前阵子鼠标滚轮使用时总会出现上下跳动比如向下滚动会往上反弹或者是在当前框架卡住但颤动的情况,这个问题困扰了我很久,试过了很多设置和驱动方面的办法都没解决,因此大概率是滚轮那有脏东西了。最后终于在一个答复下面看到了一种不用拆开修…...

CSS【常用CSS样式、盒子模型、定位、浮动 、扩展样式】--学习JavaEE的day46
day46 CSS 练习 页面实现: 分析: 未优化: 优化: 参考代码:(包含样式优化–选择器CSS属性) 先写上table方便实现,之后再去除即可 name没有服务器,可暂时不写 <!…...

os.path 提供用于处理文件路径和文件的系统函数
在Python中,os.path模块提供了一系列用于处理文件路径和文件的系统函数。 获取文件路径信息 os.path.abspath(): 获取文件的绝对路径。os.path.dirname(): 获取文件路径的目录名。os.path.basename(): 获取文件路径的文件名。os.path.split(): 分割路径为目录和文件…...
golang通过go-aci适配神通数据库
1. go-aci简介 go-aci是神通数据库基于ACI(兼容Oracle的OCI)开发的go语言开发接口,因此运行时需要依赖ACI驱动和ACI库的头文件。支持各种数据类型的读写、支持参数绑定、支持游标范围等操作。 2. Linux部署步骤 2.1. Go安装: 版本:1.9以上…...
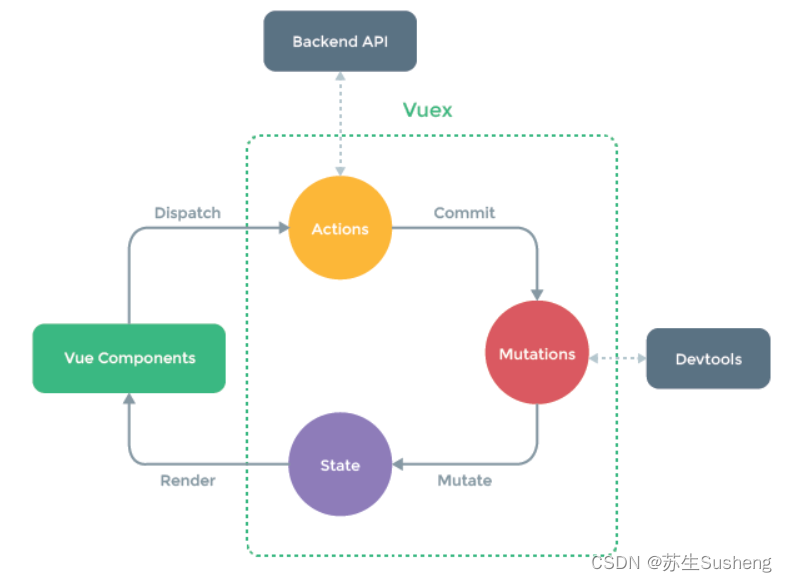
【Vue】Vue2中的Vuex
目录 Vuex介绍Vuex 中的核心概念 在vue2中使用Vuex安装 Vuex创建一个 Vuex Store在 Vue 实例中使用 Vuex编写 Vuex 的 state、mutations 和 actions在组件中使用 Vuex Vuex的核心State组件中获取 Vuex 的状态mapState 辅助函数对象展开运算符 Getter基本使用示例 通过属性访问通…...

前端生成二维码
直接img标签显示 npm i use_qrcode npm包地址 <img :src"qrcode" alt"QR Code" /> const txt: any ref(https://baidu.com) const qrcode useQRCode(txt) const qrcodeLogo useQRCode(txt, { logoSrc: https://www.antdv.com/assets/logo.1ef800…...

wordpress woocommer 添加代码实现,点击按钮,将产品添加到购物车并且跳转到结账页面
wordpress woocommer 添加代码实现,点击按钮,将产品添加到购物车并且跳转到结账页面 案列代码1,解决的是普通产品的 //短代码生成按钮,传入短代码,点击直接到达结账页面 function add_product_to_cart_button($atts)…...

Scala学习笔记6: 类
目录 第六章 类1- 简单类和无参方法2- 带有getter和setter的属性3- 只带getter的属性4- 对象私有化5- 辅助构造器6- 主构造器7- 嵌套类end 第六章 类 在Scala中, 类用于创建对象的蓝图; 类可以包含方法、值、变量、类型、对象和特质等成员; 类名应该以大写字母开头, 可以包含…...

JS数组根据对象的某一个字段排序
const person [{ name: aa, age: 9 },{ name: bb, age: 17 },{ name: cc, age: 6 },{ name: dd, age: 18 }];// 升序const arr1 person.sort((a, b) > {return a.age - b.age;b})console.log(arr1)// 降序const arr2 person.sort((a, b) > {return b.age - a.age;})co…...

JavaScript操作
做UI自动化的时候,有些操作无法直接通过selenium自带方法操 作成功,那么就需要借助前端js操作实现。 比如浏览器的滚动条这种不是html页面的内容,无法直接通过selenium 控制到。需要借助JavaScript控制。比如有些点击操作无法通过普通点击鼠…...

雪花算法 代码
/*** author lwh* date 2023/9/5* description 批量插入,手动设置**/ public class IdWorker {//因为二进制里第一个 bit 为如果是 1,那么都是负数,但是我们生成的 id 都是正数,所以第一个 bit 统一都是 0。//机器ID 2进制5位 3…...
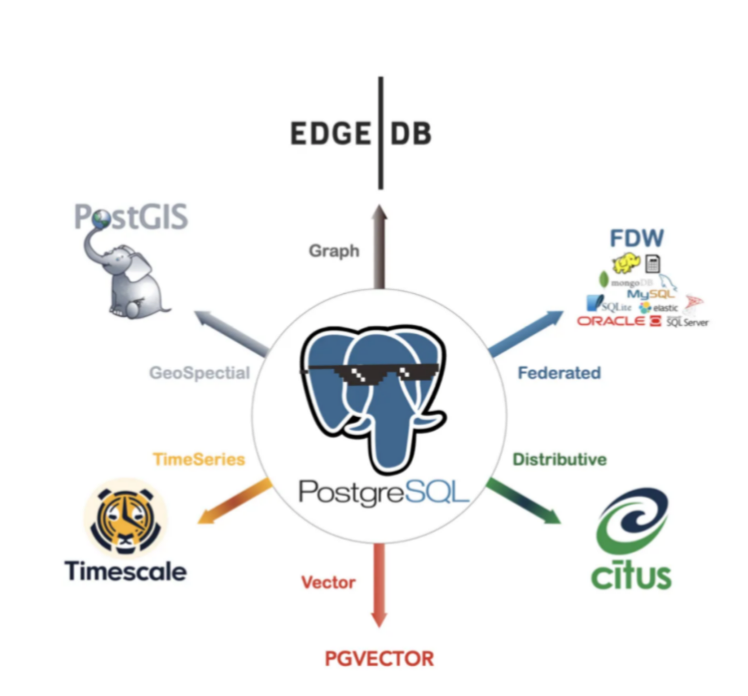
我把PostgreSQL最核心的插件撸干净了!!!
作者:IT邦德 中国DBA联盟(ACDU)成员,10余年DBA工作经验, Oracle、PostgreSQL ACE CSDN博客专家及B站知名UP主,全网粉丝10万 擅长主流Oracle、MySQL、PG、高斯及Greenplum备份恢复, 安装迁移,性能优化、故障…...

Transformer详解(1)-结构解读
Transormer块主要由四个部分组成,注意力层、位置感知前馈神经网络、残差连接和层归一化。 1、注意力层(Multi-Head Attention) 使用多头注意力机制整合上下文语义,它使得序列中任意两个单词之间的依赖关系可以直接被建模而不基于传统的循环结构&#…...

使用Flask Swagger自动生成API文档
文章目录 安装Flask Swagger使用Flask Swagger生成API文档总结1. 自动化文档生成2. 交互式文档展示3. 规范化API设计4. 提升协作效率5. 支持多种格式 Flask Swagger是一种用于管理Flask API文档的工具。它基于OpenAPI规范,可以自动生成API的交互式文档。使用Flask S…...

操作系统408考研-经典例题
什么是操作系统?答:操作系统,是计算机系统中最基本、最重要的系统软件,是其它软件 的***支撑***。控制和管理计算机系统的硬件和软件资源,合理的组织计算机工 作流程,并为用户使用计算机提供公共和基本的服务 2.多道程序 (multiprogrammming) 和多重处理 (multiprocessi…...
工程项目管理系统源码与Spring Cloud:实现高效系统管理与二次开发
随着企业规模的不断扩大和业务的快速发展,传统的工程项目管理方式已经无法满足现代企业的需求。为了提高工程管理效率、减轻劳动强度、提高信息处理速度和准确性,企业需要借助先进的数字化技术进行转型。本文将介绍一款采用Spring CloudSpring BootMybat…...

react中hook 函数的使用
以 use 开头的函数被称为 Hook。useState 是 React 提供的一个内置 Hook。你可以在 React API 参考 中找到其他内置的 Hook。你也可以通过组合现有的 Hook 来编写属于你自己的 Hook。 Hook 比普通函数更为严格。你只能在你的组件(或其他 Hook)的 顶层 调…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
