【数据结构】解决顺序表题的基本方法

🚀write in front🚀
📜所属专栏:> 初阶数据结构
🛰️博客主页:睿睿的博客主页
🛰️代码仓库:🎉VS2022_C语言仓库
🎡您的点赞、关注、收藏、评论,是对我最大的激励和支持!!!
关注我,关注我,关注我,你们将会看到更多的优质内容!!

文章目录
- 前言
- 一.空间换时间的方式:
- 二.多指针方式:
- 总结
前言
大家在处理数组相关的oj题时,一般通过遍历的方式,但是这样会导致时间复杂度非常的高。下面我来介绍一下通过空间换时间和双指针的方式减小时间复杂度!
一.空间换时间的方式:
栗子:
原地移除数组中所有的元素val,要求时间复杂度为O(N),空间复杂度为O(1)。oj题
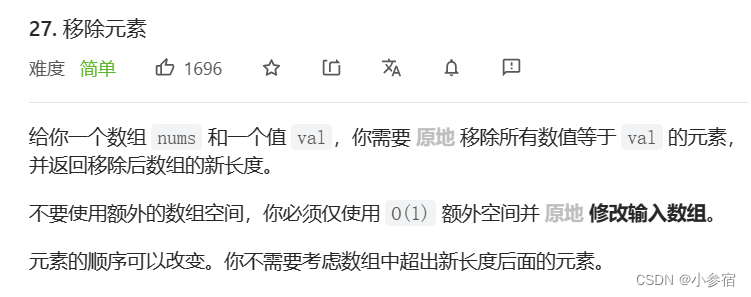
家人们刚开始做这题时很可能会通过遍历数组,然后将后面的数字往前移,这样就会导致时间复杂度非常高。
这个时候我们就可以通过牺牲空间,节省时间的方式来降低时间复杂度。
通过创建一个新数组,来保存保留的数据,这样就通过牺牲空间节省了时间。但是这题需要空间复杂度为O(1),说明不能创建额外的n个空间,那么我们该怎么办呢?下面的双指针方式会告诉你如何去做,可以先看看代码:
void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n)
{int end1=m-1,end2=n-1,dst=m+n-1;while(end1>=0&&end2>=0){if(nums1[end1]>nums2[end2]){nums1[dst--]=nums1[end1--];}else{nums1[dst--]=nums2[end2--];}}while(end2>=0){nums1[dst--]=nums2[end2--];}
}

二.多指针方式:
这里我们指的指针,在数组里面可以用数字来代替,因为数组是可以通过[]访问的,但是后面链表所用的指针就是真的指针了。
多指针的使用是非常重要的方法,但是非常依赖画图,所以只要同学们多画图,此类题目不会很难解决。
栗子:
合并两个有序数组oj题
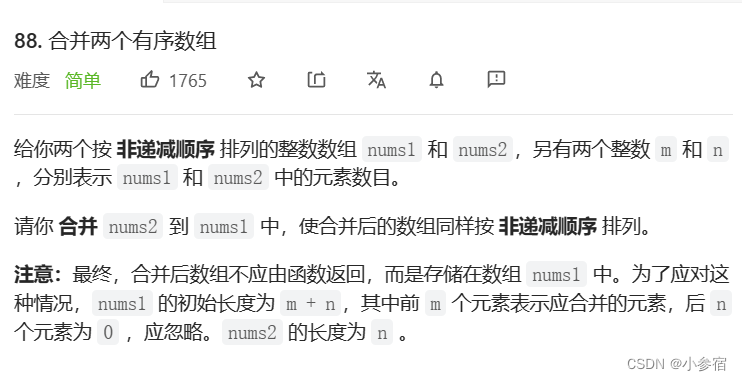
对于合并两个有序数组,兄弟们很有可能将两个数组合并,然后进行排序。然而,这样编写的后果是时间复杂度会比较高。
我们创建一个新数组(牺牲空间),通过两个数字分别标记两个数组,通过比较,得到最终的排好序的数组。

然而这道题的数组空余部分是0,所以我们要从后往前排序,并且在原数组里排序,这个时候也需要通过两个指针来标记。

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n)
{int end1=m-1,end2=n-1,dst=m+n-1;while(end1>=0&&end2>=0){if(nums1[end1]>nums2[end2]){nums1[dst--]=nums1[end1--];}else{nums1[dst--]=nums2[end2--];}}while(end2>=0){nums1[dst--]=nums2[end2--];}
}
总结
总的来说,这两种方法就是解决顺序表的主题思路。对于数据结构,家人们一定不要空想,要多通过画图解决问题。
更新不易,辛苦各位小伙伴们动动小手,👍三连走一走💕💕 ~ ~ ~ 你们真的对我很重要!最后,本文仍有许多不足之处,欢迎各位认真读完文章的小伙伴们随时私信交流、批评指正!
专栏订阅:
每日一题
c语言学习
算法
智力题
初阶数据结构
更新不易,辛苦各位小伙伴们动动小手,👍三连走一走💕💕 ~ ~ ~ 你们真的对我很重要!最后,本文仍有许多不足之处,欢迎各位认真读完文章的小伙伴们随时私信交流、批评指正!

相关文章:

【数据结构】解决顺序表题的基本方法
🚀write in front🚀 📜所属专栏:> 初阶数据结构 🛰️博客主页:睿睿的博客主页 🛰️代码仓库:🎉VS2022_C语言仓库 🎡您的点赞、关注、收藏、评论࿰…...
HDFS如何解决海量数据存储及解决方案详解
HDFS组件 HDFS组件的基准测试 说明 一般在搭建完集群之后,运维人员需要对集群进行压力测试,对于HDFS来讲,主要是读写测试写入测试 hadoop jar /export/server/hadoop-3.3.0/share/hadoop/mapreduce/hadoop-mapreduce-client-jobclient-3.…...
认识CSS值如何提高写前端代码的效率
🌟所属专栏:前端只因变凤凰之路🐔作者简介:rchjr——五带信管菜只因一枚😮前言:该系列将持续更新前端的相关学习笔记,欢迎和我一样的小白订阅,一起学习共同进步~👉文章简…...

MySQL知识点全面总结3:Mysql高级篇
三.MySQL知识点全面总结3:mysql高级篇 1.mysql语句的执行过程? 2.myesql事务详解? 3.mysql日志详解? 4.mysql的索引功能详解? 5.mysql的存储引擎详解? 6.mysql事务提交后数据与硬盘如何交互存储&…...

Spring注解开发之组件注册(二)
Spring注解开发之组件注册(一) 5.Import 给容器导入一个组件 给容器中注册组件 一、包扫描 组件标注注解(Controller/Service/Repository/Component) [自己写的类] 二、Bean [导入的第三包里面的组件] 三、Import [快速给容器中导入组件] (Import{…...

【web前端开发】CSS最常用的11种选择器
文章目录1.CSS介绍2.CSS的语言规则3.CSS的引入方式4.选择器标签选择器类选择器id选择器通配符选择器复合选择器后代选择器子代选择器并集选择器交集选择器伪类选择器hover伪类选择器active伪类选择器结构伪类选择器结语1.CSS介绍 CSS (Cascading Style Sheets,层叠样…...

微电影广告发展的痛点
微电影广告以不可阻挡之势进入大众生活中,企业利用微电影广告来进行企业形象塑造的例子比比皆是。于是乎,微电影广告在为企业塑造品牌形象方面上取得了可喜的效果,但也不可忽视,在这个发展过程中,微电影广告所面临的问…...
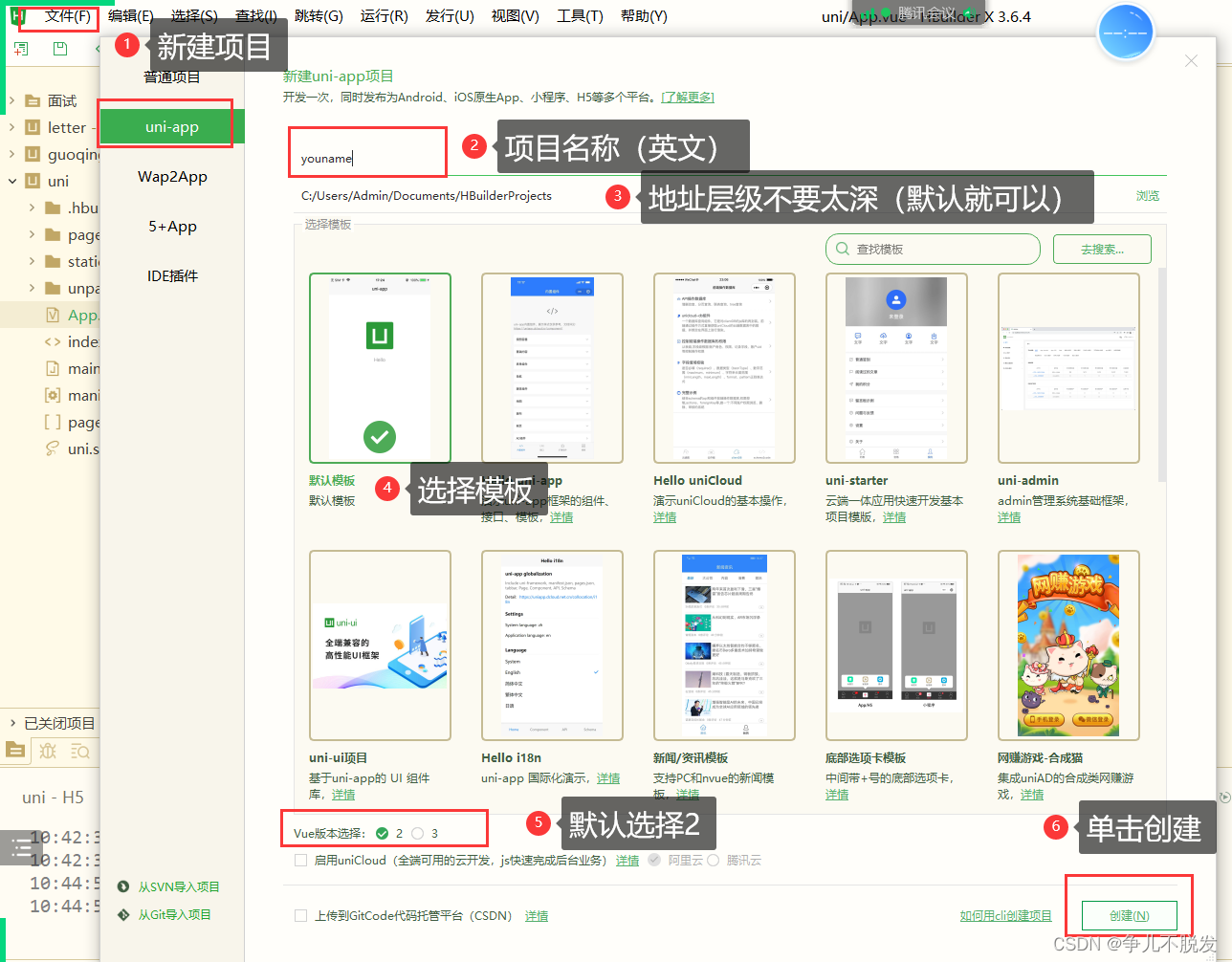
uniapp新手入门
前言: 这篇文章主要写的是uniapp的基础知识,可以让大家快速上手uniapp,同时避掉一些可能踩到的坑。 一. 什么是uniapp uniapp是由dcloud 公司开发的多端融合框架。uniapp的出现让我们的开发更为方便,一次开发,多端运行…...

linux segfault at 问题定位实践
问题:程序崩溃,打印为:app[13016]: segfault at 7fb668d29930 ip 00007fb668d3c23c sp 00007fb668e7de20 error 7 in mydefine.so[7fb668d3400011000]定位步骤:基础分析数据,大概了解反馈信息(根据chatGPT&…...

SpringCloud+SpringCloudAlibaba
架构的演进1.1单体架构将所有业务场景的表示层、业务逻辑层和数据访问层放在一个工程中,最终经过编译、打包,部署在一台服务器上。◆ 1.1.1单体架构的优点1)部署简单: 由于是完整的结构体,可以直接部署在一个服务器上即可。2&…...
【独家】)
华为OD机试 - 路灯照明(C 语言解题)【独家】
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧文章目录 使用说明本期题目:路灯照明…...
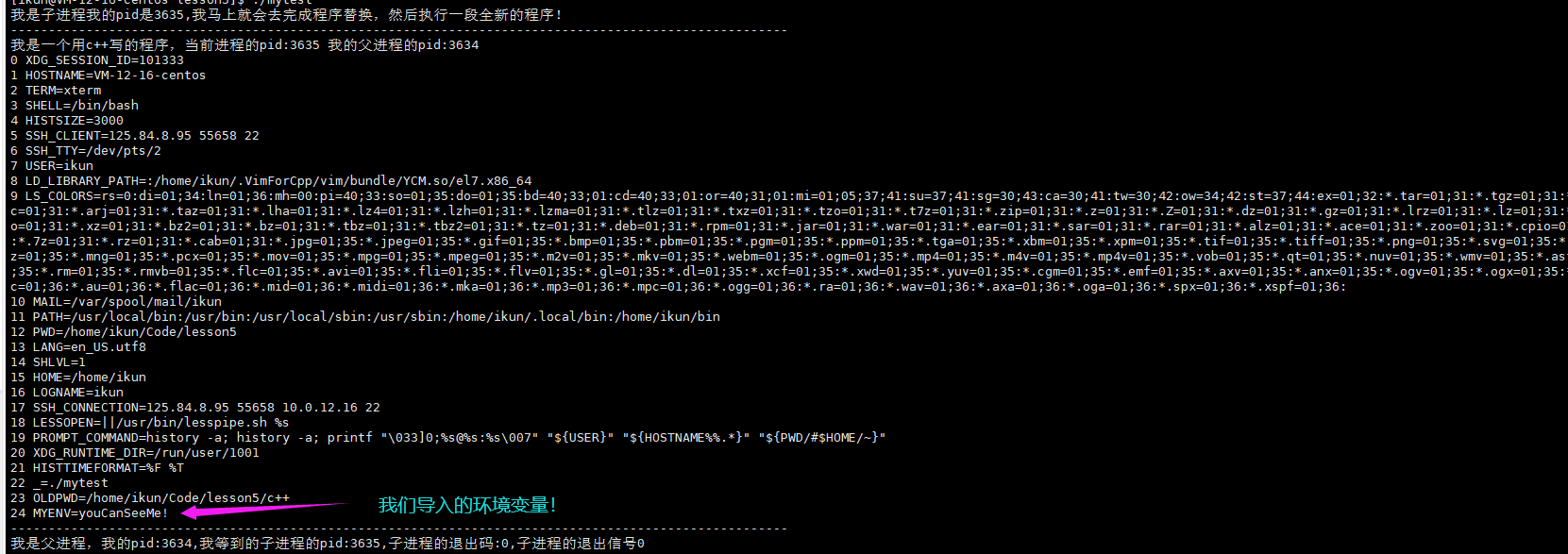
Linux程序替换
Linux程序替换创建子进程的目的?程序替换如何实现程序替换?什么是程序替换?先见一见单进程版本的程序替换程序替换原理多进程版本的程序替换execl函数组简易版Shell创建子进程的目的? 目的:为了帮助父进程完成一些特定的任务&…...

@JsonFormat @DataTimeFormat 时间格式
省流:用JsonFormat即可有时候会看到入参dto里,在时间类型的变量上用DateTimeFormat,代码如下。public class XXXdto{DateTimeFormat(pattern "yyyy-MM-dd hh:mm:ss")private Date startDate; }这是为了入参传日期格式的值。即前端…...
带你玩转modbusTCP通信
modbus TCP Modbus TCP是一种基于TCP/IP协议的Modbus通信协议,它是Modbus协议的一种变体,用于在以太网上进行通信。Modbus TCP协议是一种开放的通信协议,它支持多种编程语言和操作系统,并且可以在不同的硬件和软件平台上进行通信…...
T2交替)
2021牛客OI赛前集训营-提高组(第三场)T2交替
2021牛客OI赛前集训营-提高组(第三场) 题目大意 一个长度为nnn的数组aaa,每秒都会变成一个长度为n−1n-1n−1的新数组a′aa′,其变化规则如下 如果当前数组aaa的大小nnn为偶数,则对于新数组a′aa′的每一个位置i(1≤…...

论文投稿指南——中文核心期刊推荐(金融)
【前言】 🚀 想发论文怎么办?手把手教你论文如何投稿!那么,首先要搞懂投稿目标——论文期刊 🎄 在期刊论文的分布中,存在一种普遍现象:即对于某一特定的学科或专业来说,少数期刊所含…...
【独家】)
华为OD机试 - 不等式(C 语言解题)【独家】
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧文章目录 使用说明本期题目:不等式题…...
90后老板用低代码整顿旅行社,创2000万年收,他是怎么做到的?(真实)
热爱旅游的92年成都小伙猴哥,大学毕业后开了一家旅行社,主要从事川藏、云南定制游服务。 从今年春节开始,国内各地旅游业开始复苏,向旅行社打电话咨询的人越来越多。 旅游的人多是好事,也是一种烦恼,因为…...

Apache Dubbo 存在反序列化漏洞(CVE-2023-23638)
漏洞描述 Apache Dubbo 是一款轻量级 Java RPC 框架 该项目受影响版本存在反序列化漏洞,由于Dubbo在序列化时检查不够全面,当攻击者可访问到dubbo服务时,可通过构造恶意请求绕过检查触发反序列化,执行恶意代码 漏洞名称Apache …...

【YOLO】YOLOv8训练自定义数据集(4种方式)
YOLOv8 出来一段时间了,继承了分类、检测、分割,本文主要实现自定义的数据集,使用 YOLOV8 进行检测模型的训练和使用 YOLOv8 此次将所有的配置参数全部解耦到配置文件 default.yaml,不再类似于 YOLOv5,一部分在配置文件…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...
