逻辑分析仪 - 采样率/采样深度
采样深度(Sampling Depth)
采样深度指的是逻辑分析仪在一次捕获过程中可以记录的最大样本数量。简单来说,采样深度越大,逻辑分析仪可以记录的数据量就越多。这对于分析长时间的信号变化或复杂的信号序列非常重要。
采样率(Sampling Rate)
采样率是逻辑分析仪每秒钟采集样本的次数,通常以赫兹(Hz)或每秒样本数(Samples Per Second, SPS)为单位。采样率越高,逻辑分析仪捕获信号的时间分辨率就越高,能够捕捉到更快的信号变化。
一般而言,我们的采样率要设置成被采样信号频率的5-10倍最好。
采样深度和采样率的关系
采样深度和采样率之间的关系可以通过如下公式来表示:
采样深度 = 采样率 * 采样时间
示例分析:
假设逻辑分析仪的采样率为100 MHz(每秒1亿个样本),如果我们希望捕获1秒钟的信号数据,则需要的采样深度为:
![[ 采样深度 = 100 , \text{MHz} \times 1 , \text{s} = 100 , \text{M样本} ]](https://img-blog.csdnimg.cn/direct/ac1f10a786d748d491e26e72b1685cbb.png)
如果采样深度固定,而我们需要延长捕获时间,则必须降低采样率。例如,如果采样深度为100 M样本,而我们希望捕获2秒钟的数据,则采样率必须降至:
![[ 采样率 = \frac{采样深度}{采样时间} = \frac{100 , \text{M样本}}{2 , \text{s}} = 50 , \text{MHz} ]](https://img-blog.csdnimg.cn/direct/f4d77fd842eb49628a0f3067e0662e79.png)
选择合适的采样深度和采样率
- 高采样率:适用于捕获高频信号或快速信号变化。适用于高速数字电路的调试。
- 大采样深度:适用于需要长时间捕获信号的情况,如监测系统运行状态、捕捉罕见事件。
注意事项
- 存储限制:采样深度受逻辑分析仪的内存容量限制。
- 信号特性:选择采样率时需考虑信号的最高频率。一般来说,采样率应至少是信号最高频率的2倍(奈奎斯特采样定理)。
通过正确理解和选择采样深度和采样率,可以更有效地使用逻辑分析仪来调试和分析嵌入式系统中的信号。
希望这些信息对你有所帮助,城哥!如果有其他问题,欢迎继续交流。
参考资料
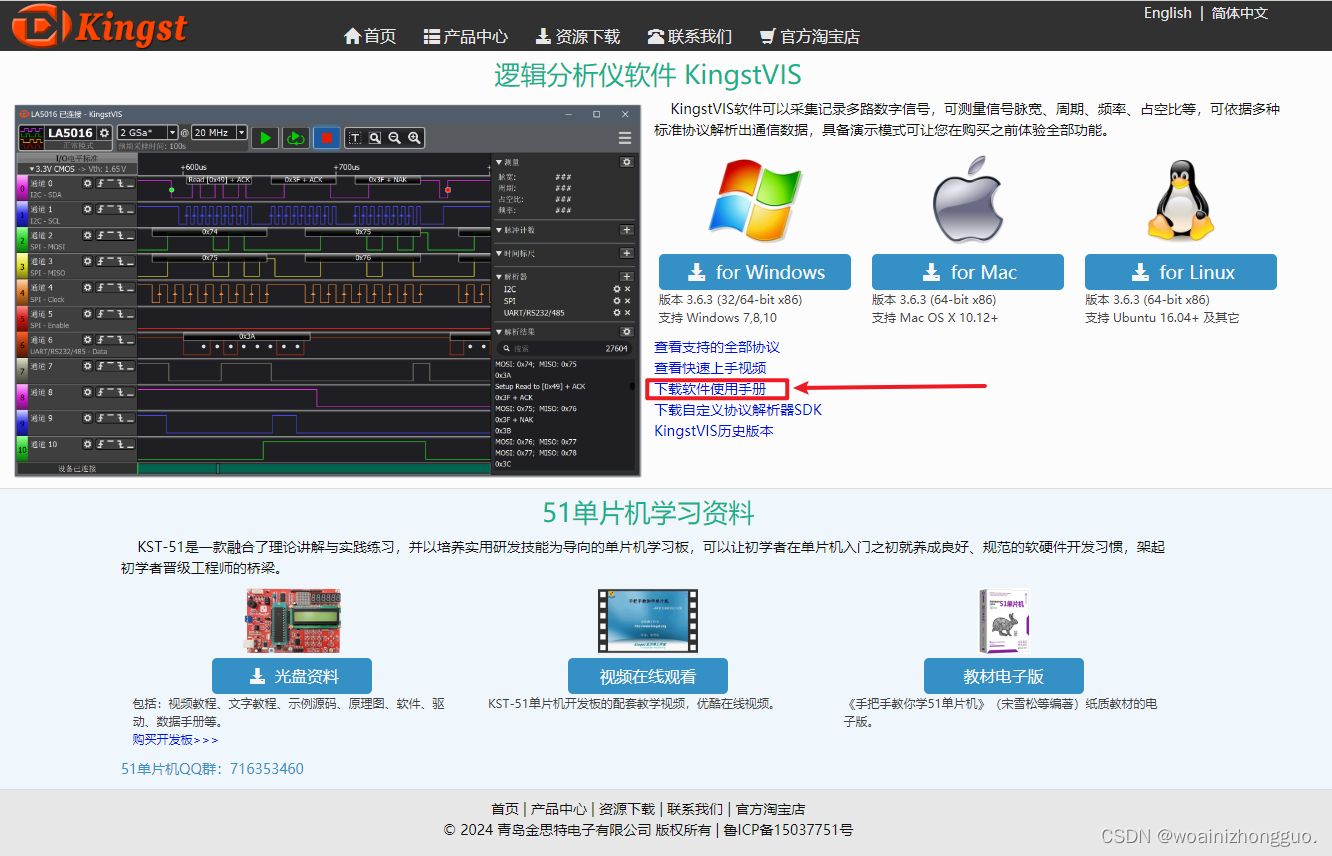
逻辑分析仪卖家官网
相关文章:

逻辑分析仪 - 采样率/采样深度
采样深度(Sampling Depth) 采样深度指的是逻辑分析仪在一次捕获过程中可以记录的最大样本数量。简单来说,采样深度越大,逻辑分析仪可以记录的数据量就越多。这对于分析长时间的信号变化或复杂的信号序列非常重要。 采样率&#…...

【Maven打包将resources/lib/下的jar也打包进jar包中】
Maven打包将resources/lib/下的jar也打包进jar包中 !!!少走弯路 第一步 resources/lib/下引入jar ftp4j-1.7.2.jar替换为自己jar包的名称 <dependency><groupId>it.sauronsoftware.ftp4j</groupId><artifactId>ft…...

基于Java的地震震中附近城市分析实战
目录 前言 一、空间数据说明 1、空间查询 二、Java后台开发 1、模型层设计与实现 2、控制层设计与实现 三、Leaflet地图开发 1、地震震中位置展示 2、附近城市展示 3、成果展示 总结 前言 随着全球气候变化和地壳活动的不断演变,地震作为一种自然灾害&…...

【C语言】指针(三)
目录 一、字符指针 1.1 ❥ 使用场景 1.2 ❥ 有关字符串笔试题 二、数组指针 2.1 ❥ 数组指针变量 2.2 ❥ 数组指针类型 2.3 ❥ 数组指针的初始化 三、数组指针的使用 3.1 ❥ 二维数组和数组名的理解 3.2 ❥ 二维数组传参 四、函数指针 4.1 ❥ 函数的地址 4.2 ❥ 函数…...

【Linux】从零开始认识进程间通信 —— 管道
送给大家一句话: 人要成长,必有原因,背后的努力与积累一定数倍于普通人。所以,关键还在于自己。 – 杨绛 从零开始认识进程间通信 1 为什么要进程间通信2 进程如何通信3 进程通信的常见方式4 管道4.1 什么是管道4.2 管道通信的系…...

Top3专业课150满分,怎么考的?
这个系列会邀请上岸学长学姐进行经验分享~ 今天经验分享的同学是小马哥上海交大819的全程班学员,专业课150分满分,这位同学也是819期末考试的第一名,非常厉害!大家吸吸欧气! 初试成绩单 前言 先介绍下自己࿰…...
要点总结)
Windows Presentation Foundation(WPF)要点总结
Windows Presentation Foundation(WPF)是微软推出的一种用于构建Windows桌面应用程序的框架。自从WPF在.NET Framework 3.0中引入以来,它以其强大的功能和灵活性,逐渐成为开发人员构建现代、富用户界面应用程序的首选。本文将概述…...

【研发日记】嵌入式处理器技能解锁(一)——多任务异步执行调度的三种方法
文章目录 前言 Timer中断调度 Event中断调度 StateFlow调度 分析和应用 总结 参考资料 前言 近期在一些嵌入式系统开发项目中,在使用嵌入式处理器时,遇到了挺多费时费力的事情。所以利用晚上和周末时间,在这些方面深入研究了一下&…...

揭秘Python的魔法:装饰器的超能力大揭秘 ♂️✨
文章目录 Python进阶之装饰器详解1. 引言装饰器的概念与意义装饰器在Python编程中的作用 2. 背景介绍2.1 函数作为对象2.2 高阶函数 3. 装饰器基础3.1 理解装饰器3.2 装饰器的工作原理 4. 带参数的装饰器4.1 为什么需要带参数4.2 实现带参数的装饰器使用函数包裹装饰器使用类实…...

怎么一键消除路人?教你三个消除方法
怎么一键消除路人?在数字时代,摄影已成为我们记录生活、表达情感的重要方式。然而,完美的照片背后往往隐藏着一些不那么完美的元素——比如那些不经意间闯入镜头的路人。他们或许只是匆匆过客,但却足以破坏你精心构图的美好瞬间。…...

Android Settings系统属性读写
Settings系统属性存储均为xml,分三种: 1.global:所有的偏好设置对系统的所有用户公开,第三方APP有读没有写的权限; 源码地址:frameworks/base/core/java/android/provider/Settings.java 对应xml路径&…...

2024年,企业的人才管理怎么做?这5点是关键!
当今时代,各行各业都面临着激烈的竞争。这些竞争归根结底都是人才的竞争。企业若想在竞争中掌握主动权,实现基业长青,就必须努力留住人才,并充分发挥他们的积极性、主动性和创造性。因此,做好人才管理是企业实现长期可…...

数据库DDL语句
数据库DDL语句: 查询所有数据库: show databases;查询当前数据库的名称 select database();创建数据库 create database [if not exists] 数据库名 [default charset 字符集] [collate 排序规则]注意:排序规则指定后,它会影响…...

《艺术大观》知网艺术刊:可加急, 出刊上网快
《艺术大观》 《艺术大观》征文通知 《艺术大观》期刊诚邀学者、艺术家和文化工作者积极投稿,共同探索艺术领域的前沿问题,促进学术交流和艺术创作的发展。我们欢迎各类艺术形式的研究与评论,包括但不限于绘画、雕塑、音乐、舞蹈、戏剧、电…...
如何在go语言中调用c语言代码
1.安装c语言编译器 要使用cgo,需要安装c语言编译器 gcc 2.检查CGO_ENABLED时候开启 使用以下命令查看: go env CGO_ENABLED 如果go env CGO_ENABLED被禁用(为0),需要将其设置为开启(为1) 3.编写c语言程序,并用go语言调用c语言程序 1ÿ…...

Monodle centerNet3D 瑞芯微RKNN、地平线Horizon芯片部署、TensorRT部署
一直想做一点3D目标检测,先来一篇单目3D目标检测Monodle(基于centernet的),训练代码参考官方【代码】,这里只讲讲如何部署。 模型和完整仿真测试代码,放在github上参考链接【模型和完整代码】。 1 模型训练…...

Android Studio 使用MQTT协议开发应用时怎样关闭MQTT连接
Android Studio 使用MQTT协议开发应用时怎样关闭MQTT连接 Android Studio 使用MQTT协议开发应用时关闭MQTT连接 在使用mqtt开发的时候,有时候需要通过 返回 按钮关闭界面或者Activity时,关闭当前页面使用的mqtt连接,这里有两种方式彻底销毁…...
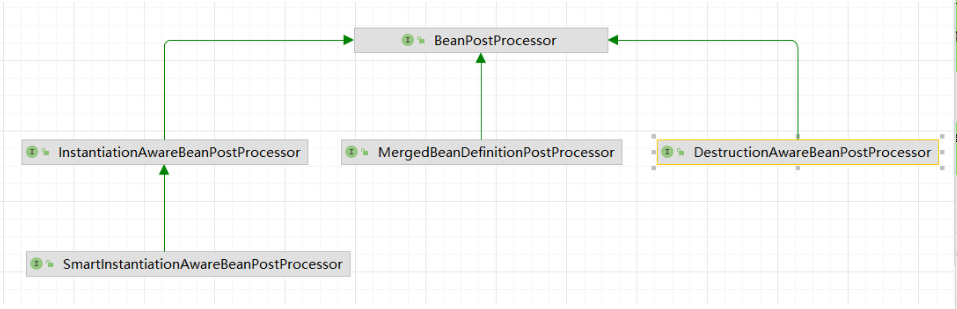
Sping源码(八)—registerBeanPostProcessors
序言 之前我们用大量的篇幅介绍过invokeBeanFactoryPostProcessors()方法的执行流程。 而invokeBeanFactoryPostProcessors的主要逻辑就是遍历执行实现了BeanDefinitionRegistryPostProcesso类(主要是针对BeanDefinition的操作)和BeanFactoryPostProcessor(主要针对BeanFacrot…...
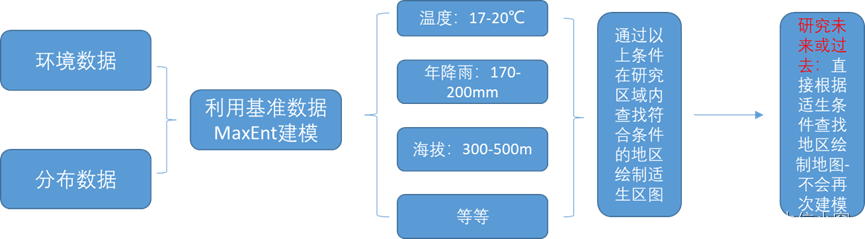
MaxEnt模型文章中存在的问题和处理方法(050B更新)2024.5.24
目前多数MaxEnt文章中存在的问题和处理方案。 **问题一:**变量数据使用问题,很多文章把所有变量数据直接使用,但是温度和土壤、植被类型等属于不同数据类型,在数据使用时参数配置是不一样的,产生的结果文件也是不一样的…...

Modular RPG Hero PBR
-掩码着色着色器提供了无限的颜色变化。(适用于标准/HDRP/URP 11.0.0) -为剑与盾/双剑/双剑姿态提供了简单的角色控制器。(不包括弓和魔杖控制器)(它是用旧的输入系统建造的) -HDRP/URP(11.0.0)SRP 100%支持常规着色器和遮罩着色着色器(基于着色器图形) -具有许多模块…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

TCP/IP 网络编程 | 服务端 客户端的封装
设计模式 文章目录 设计模式一、socket.h 接口(interface)二、socket.cpp 实现(implementation)三、server.cpp 使用封装(main 函数)四、client.cpp 使用封装(main 函数)五、退出方法…...

小智AI+MCP
什么是小智AI和MCP 如果还不清楚的先看往期文章 手搓小智AI聊天机器人 MCP 深度解析:AI 的USB接口 如何使用小智MCP 1.刷支持mcp的小智固件 2.下载官方MCP的示例代码 Github:https://github.com/78/mcp-calculator 安这个步骤执行 其中MCP_ENDPOI…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...

HTTPS证书一年多少钱?
HTTPS证书作为保障网站数据传输安全的重要工具,成为众多网站运营者的必备选择。然而,面对市场上种类繁多的HTTPS证书,其一年费用究竟是多少,又受哪些因素影响呢? 首先,HTTPS证书通常在PinTrust这样的专业平…...
