263 基于matlab得到的频分复用(FDM,Frequency Division Multiplexing)实现
基于matlab得到的频分复用(FDM,Frequency Division Multiplexing)实现,仿真时录入三路声音信号进行处理,将用于传输信道的总带宽划分成三个子频带,经过复用以后再将录入的声音信号恢复出来。程序已调通,可直接运行。

263 频分复用FDM 总带宽划分 恢复信号 - 小红书 (xiaohongshu.com)
相关文章:

263 基于matlab得到的频分复用(FDM,Frequency Division Multiplexing)实现
基于matlab得到的频分复用(FDM,Frequency Division Multiplexing)实现,仿真时录入三路声音信号进行处理,将用于传输信道的总带宽划分成三个子频带,经过复用以后再将录入的声音信号恢复出来。程序已调通,可直接运行。 2…...

使用v-model完成数据的双向绑定
创作灵感 面试问道了,没答出来,呜呜呜~ v-model实现双向绑定的原理 首先我们要知道,v-model实现的双向绑定其实只是props与emit的简化版本。其中,props负责父组件向子组件传递值,emit负责子组件向父组件传递值。 在…...
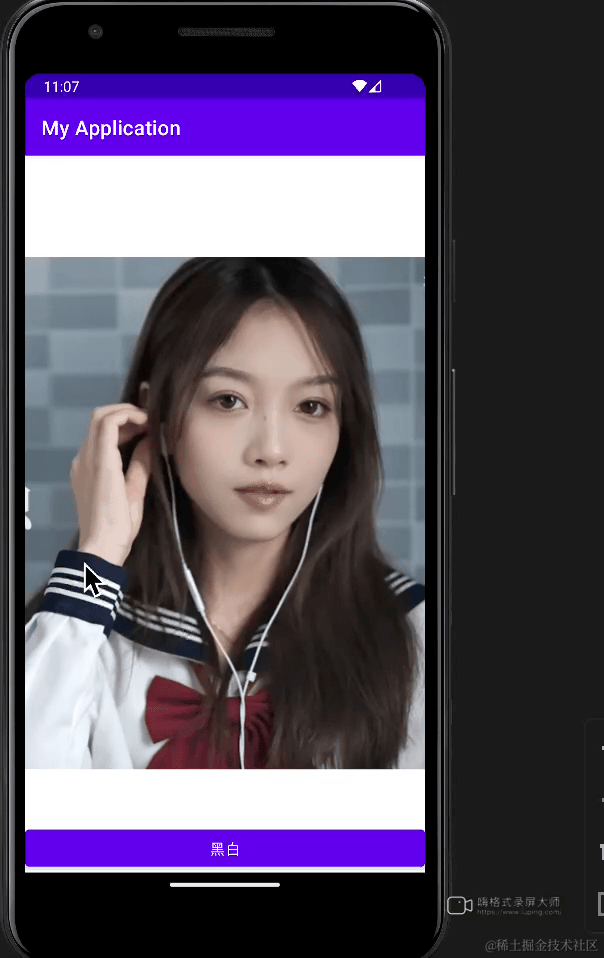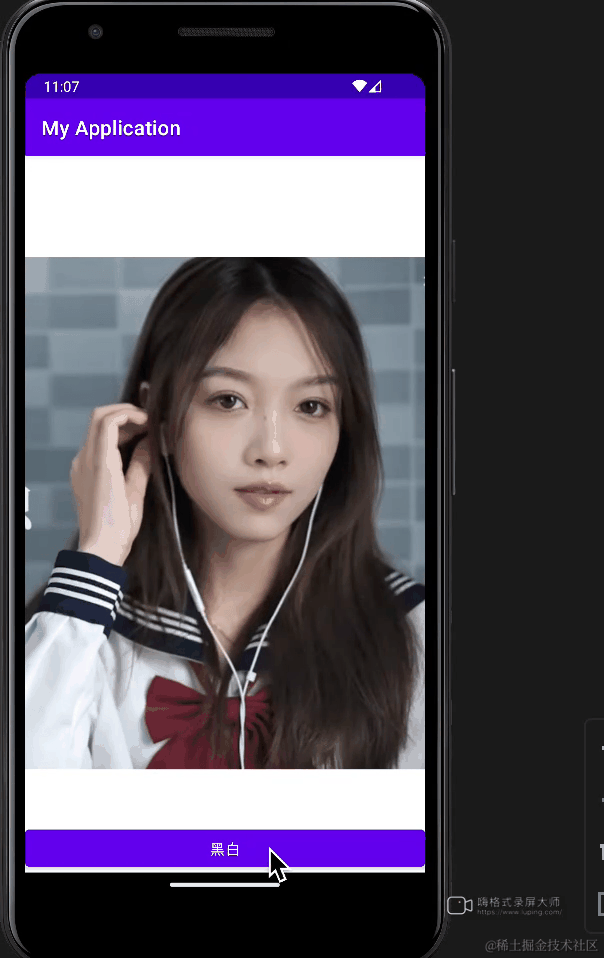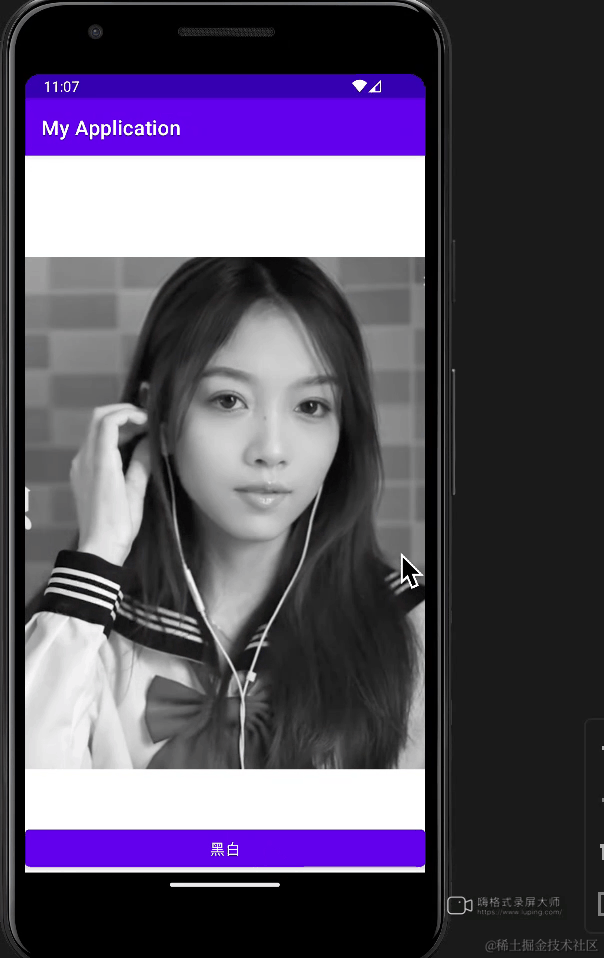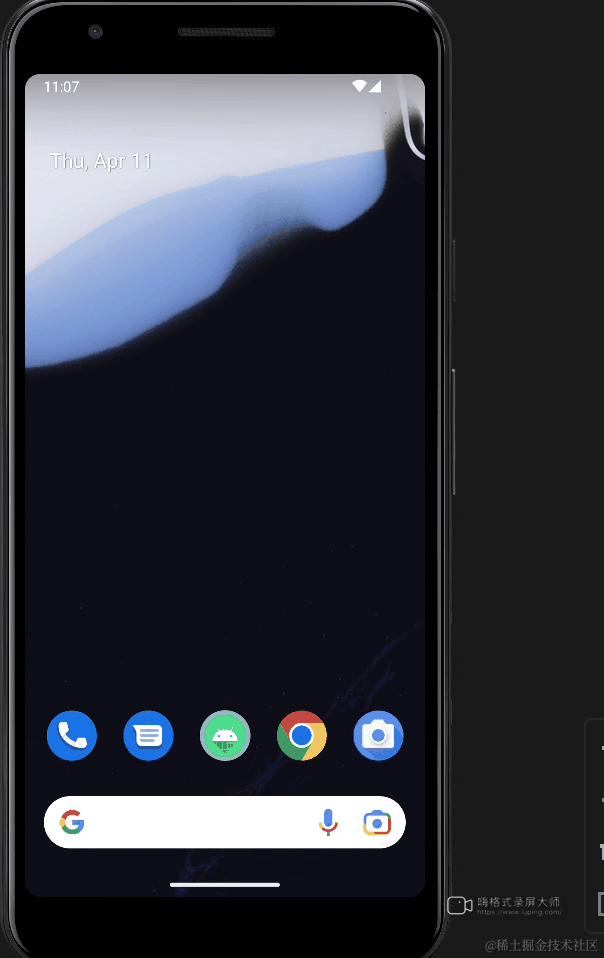
如何使用Android NDK将头像变成“遗像”
看完本文的标题,可能有人要打我。你说黑白的老照片不好吗?非要说什么遗像,我现在就把你变成遗像!好了,言归正传。我想大部分人都用过美颜相机或者剪映等软件吧,它们的滤镜功能是如何实现的,有人…...

python判断字符串是否为回文串的详细解析与实现
新书上架~👇全国包邮奥~ python实用小工具开发教程http://pythontoolsteach.com/3 欢迎关注我👆,收藏下次不迷路┗|`O′|┛ 嗷~~ 目录 一、引言:回文串的定义与背景 二、判断回文串的基本思路 示例解析 三、代码实…...
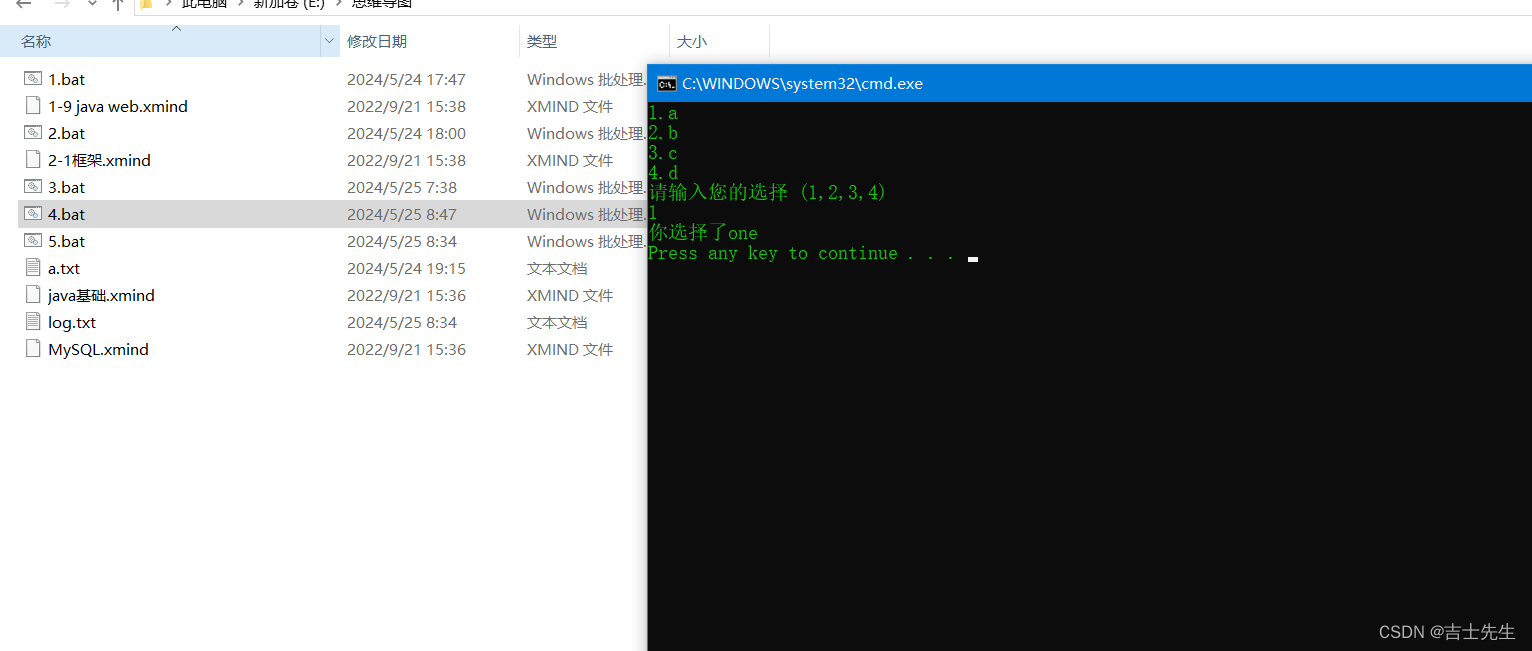
148.【Windows DOS命令脚本文件】
Window待处理脚本 (一)、批处理编程初步体验1.什么是批处理程序?(1).批处理程序的定义(2).如何编辑批处理程序 2.批处理程序可以做什么?(1).匹配规则删除文件(2).新建文件,日志等(3).创建计算机病毒等 3.一个基本的批处理文件(1).带盘符的输出…...

推荐网站(13)plantumlb自动帮我们创建 UML 图表
今天推荐一个网站plantumlb,它可以自动帮我们创建 UML 图表。 plantumlb网站中的PlantUML是一个开源工具,它允许用户使用简单的文本描述来创建UML(统一建模语言)图表。PlantUML支持多种类型的UML图表,包括用例图、类图…...
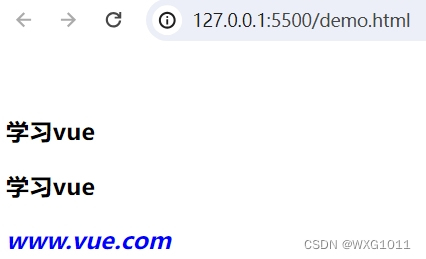
【vue-1】vue入门—创建一个vue应用
最近在闲暇时间想学习一下前端框架vue,主要参考以下两个学习资料。 官网 快速上手 | Vue.js b站学习视频 2.创建一个Vue3应用_哔哩哔哩_bilibili 一、创建一个vue3应用 <!DOCTYPE html> <html lang"en"> <head><meta charset&q…...
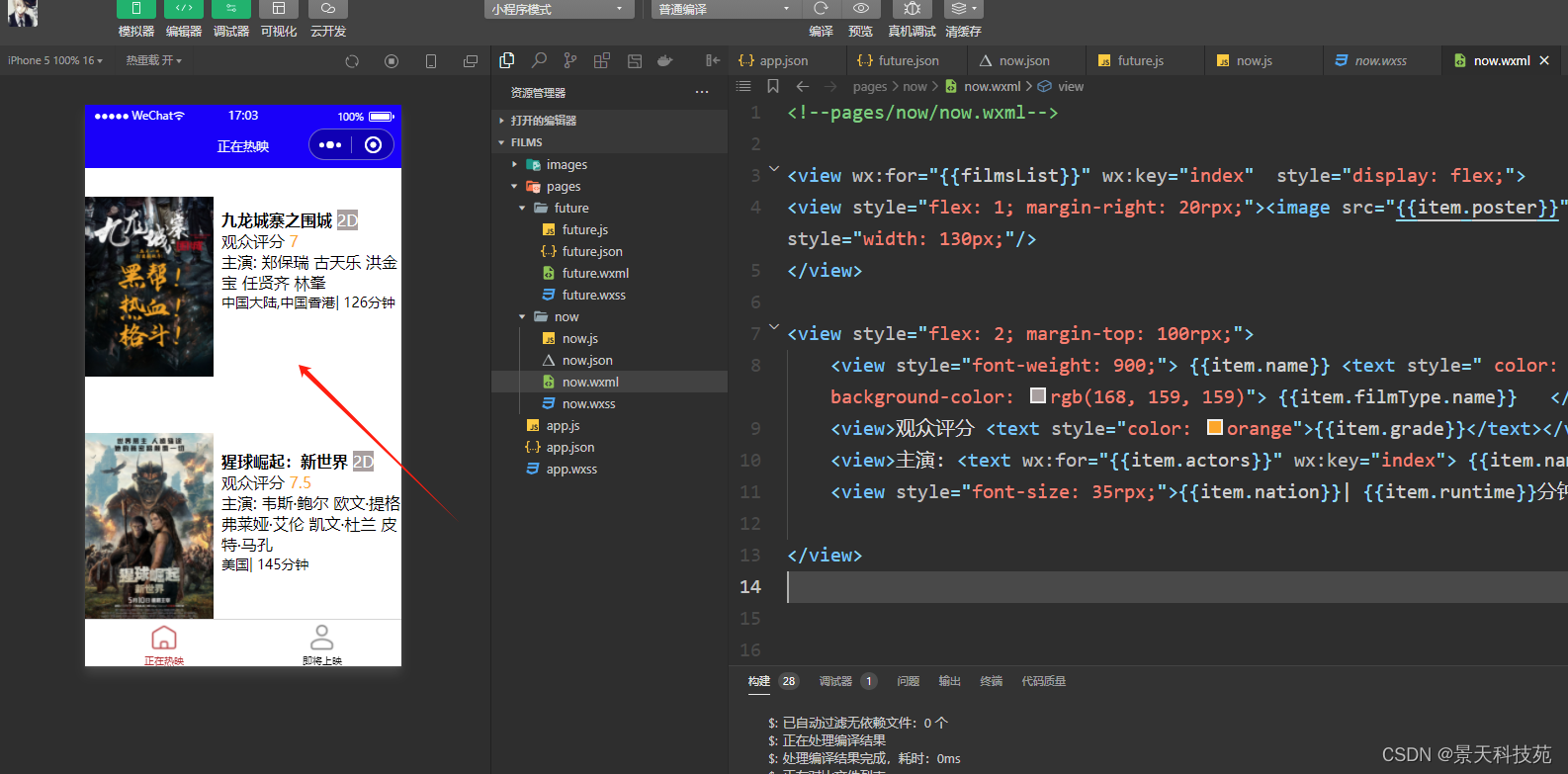
【微信小程序开发】小程序前后端交互--发送网络请求实战解析
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,…...

【NOIP2013普及组复赛】题2:表达式求值
题2:表达式求值 【题目描述】 给定一个只包含加法和乘法的算术表达式,请你编程计算表达式的值。 【输入文件】 输入仅有一行,为需要你计算的表达式,表达式中只包含数字、加法运算符 “ ” “” “”和乘法运算符 “ ∗ ” “…...
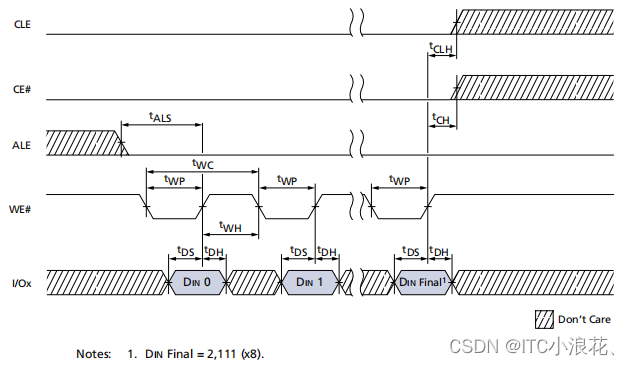
datasheet芯片数据手册—新手入门学习(二)【8-18】
参考芯片手册已经上传,可自行下载 因为芯片参考手册内容比较多,故再一次介绍本文内容主要讲解章节。 目录 8、内容介绍 命令真值表 9、Command Definitions 10、READ Operations (1)页面读取操作 (2ÿ…...
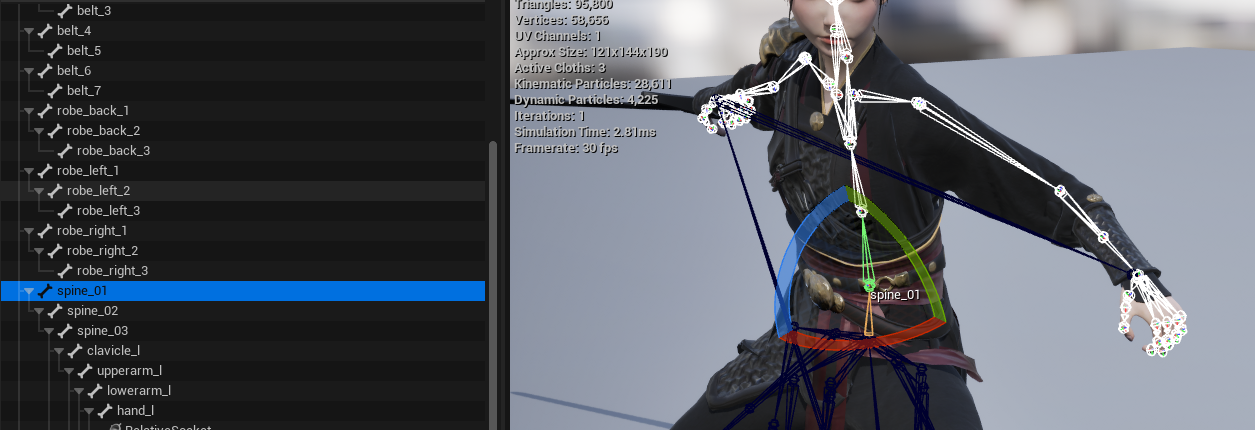
UE5 双手握剑的实现(逆向运动学IK)
UE5 双手握剑的实现 IK 前言 什么是IK? UE官方给我们提供了很多对于IK处理的节点,比如ABRIK、Two Bone IK、Full Body IK 、CCD IK等,但是看到这,很多人就好奇了,什么是IK? 首先我们来看看虚幻小白人的骨…...
及其与抽象类的区别)
Java中的接口(Interface)及其与抽象类的区别
一、技术难点 在Java中,接口是一种完全抽象的类,主要用于定义一组方法的规范,但不提供具体的实现。接口的技术难点主要体现在以下几个方面: 方法的定义与实现分离:接口只定义了方法的签名,没有方法体&…...
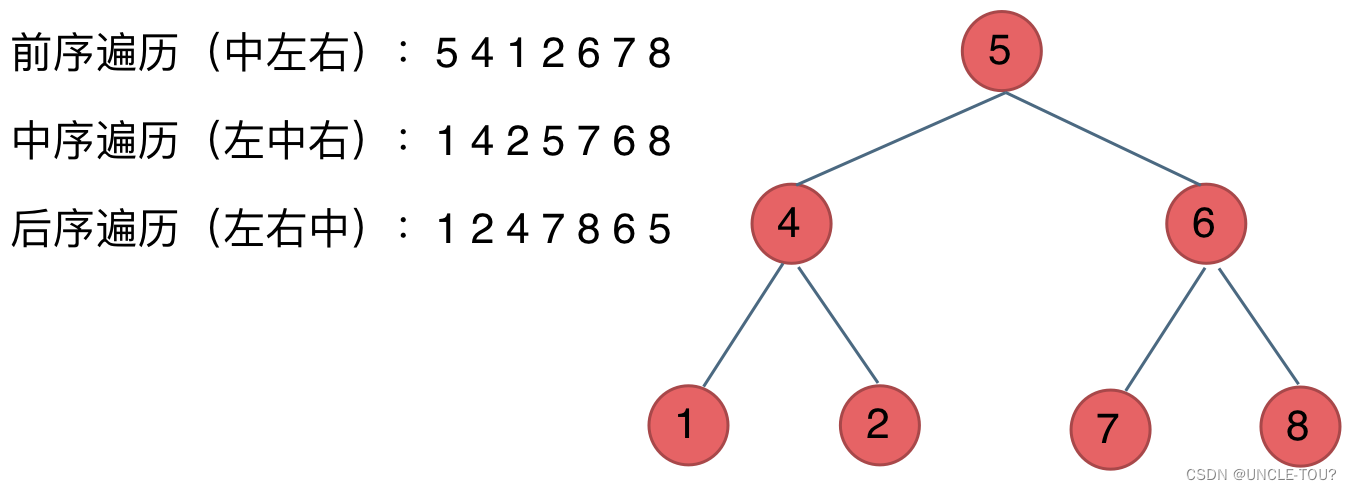
代码随想录算法训练营第十四天(py)| 二叉树 | 递归遍历、迭代遍历、统一迭代
1 理论基础 1.1 二叉树的种类 满二叉树 只有度为0和2的节点,且度为0的节点在同一层。 深度为k,有2^k-1个节点 完全二叉树 除了最底层可能没填满,其余每层节点数都达到最大。并且最底层节点全部集中在左边。 二叉搜索树 是一个有数值…...

Golang并发编程-协程goroutine初体验
文章目录 前言一、Goroutine适合的使用场景二、Goroutine的使用1. 协程初体验 三、WaitGroupWaitGroup 案例一WaitGroup 案例二 总结 前言 学习Golang一段时间了,一直没有使用过goroutine来提高程序执行效率,在一些特殊场景下,还是有必须开启…...
驱动与系统学习网址
DRM(Direct Rendering Manager)学习简介-CSDN博客 Android Qcom Display学习(零)-CSDN博客 https://blog.csdn.net/hexiaolong2009/category_9705063.htmlhttps://blog.csdn.net/hexiaolong2009/category_9705063.htmlRender Hell —— 史上最通俗易懂…...

OAuth2.0
OAuth2.0 OAuth2.0是一种授权框架,用于授权第三方应用访问用户资源的方式。它允许用户将自己的信息(如照片、视频等)存储在一个服务提供商中,然后授权第三方应用访问这些信息,而无需提供用户名和密码给第三方应用。OAu…...

测试testing10
测试testing10...
的深入解析)
在Java中实现泛型(Generics)的深入解析
在Java中,泛型(Generics)是一个强大的工具,它允许我们在编译时定义类型参数,使代码更加灵活、可重用和类型安全。下面,我将从技术难点、面试官关注点、回答吸引力以及代码举例四个方面,详细解析…...

每周题解:繁忙的都市
题目链接 繁忙的都市 题目描述 城市 C 是一个非常繁忙的大都市,城市中的道路十分的拥挤,于是市长决定对其中的道路进行改造。城市 C 的道路是这样分布的:城市中有 n n n 个交叉路口,有些交叉路口之间有道路相连,两…...

linux之防火墙工具
netfilter Linux防火墙是由Netfilter组件提供的,Netfilter工作在内核空间,集成在linux内核中。 Netfilter在内核中选取五个位置放了五个hook(勾子) function(INPUT、OUTPUT、FORWARD、PREROUTING、POSTROUTING),而这五个hook function向用户…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

深入理解 React 样式方案
React 的样式方案较多,在应用开发初期,开发者需要根据项目业务具体情况选择对应样式方案。React 样式方案主要有: 1. 内联样式 2. module css 3. css in js 4. tailwind css 这些方案中,均有各自的优势和缺点。 1. 方案优劣势 1. 内联样式: 简单直观,适合动态样式和…...

二叉树-144.二叉树的前序遍历-力扣(LeetCode)
一、题目解析 对于递归方法的前序遍历十分简单,但对于一位合格的程序猿而言,需要掌握将递归转化为非递归的能力,毕竟递归调用的时候会调用大量的栈帧,存在栈溢出风险。 二、算法原理 递归调用本质是系统建立栈帧,而非…...

Springboot 高校报修与互助平台小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,高校报修与互助平台小程序被用户普遍使用,为…...

C++ Saucer 编写Windows桌面应用
文章目录 一、背景二、Saucer 简介核心特性典型应用场景 三、生成自己的项目四、以Win32项目方式构建Win32项目禁用最大化按钮 五、总结 一、背景 使用Saucer框架,开发Windows桌面应用,把一个html页面作为GUI设计放到Saucer里,隐藏掉运行时弹…...
