代码随想录算法训练营第十四天（py）| 二叉树 | 递归遍历、迭代遍历、统一迭代

1 理论基础

1.1 二叉树的种类

满二叉树

只有度为0和2的节点，且度为0的节点在同一层。
深度为k，有2^k-1个节点

完全二叉树

除了最底层可能没填满，其余每层节点数都达到最大。并且最底层节点全部集中在左边。

二叉搜索树

是一个有数值的有序树。左子树的所有节点均小于根节点，右子树的所有节点均大于根节点。

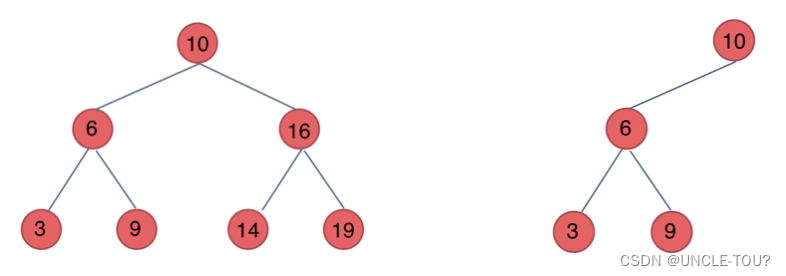
大的放右边，小的放左边。

平衡二叉搜索树。

若非空，则左右两个子树的高度差不超过1，并且两个子树都是平衡二叉树

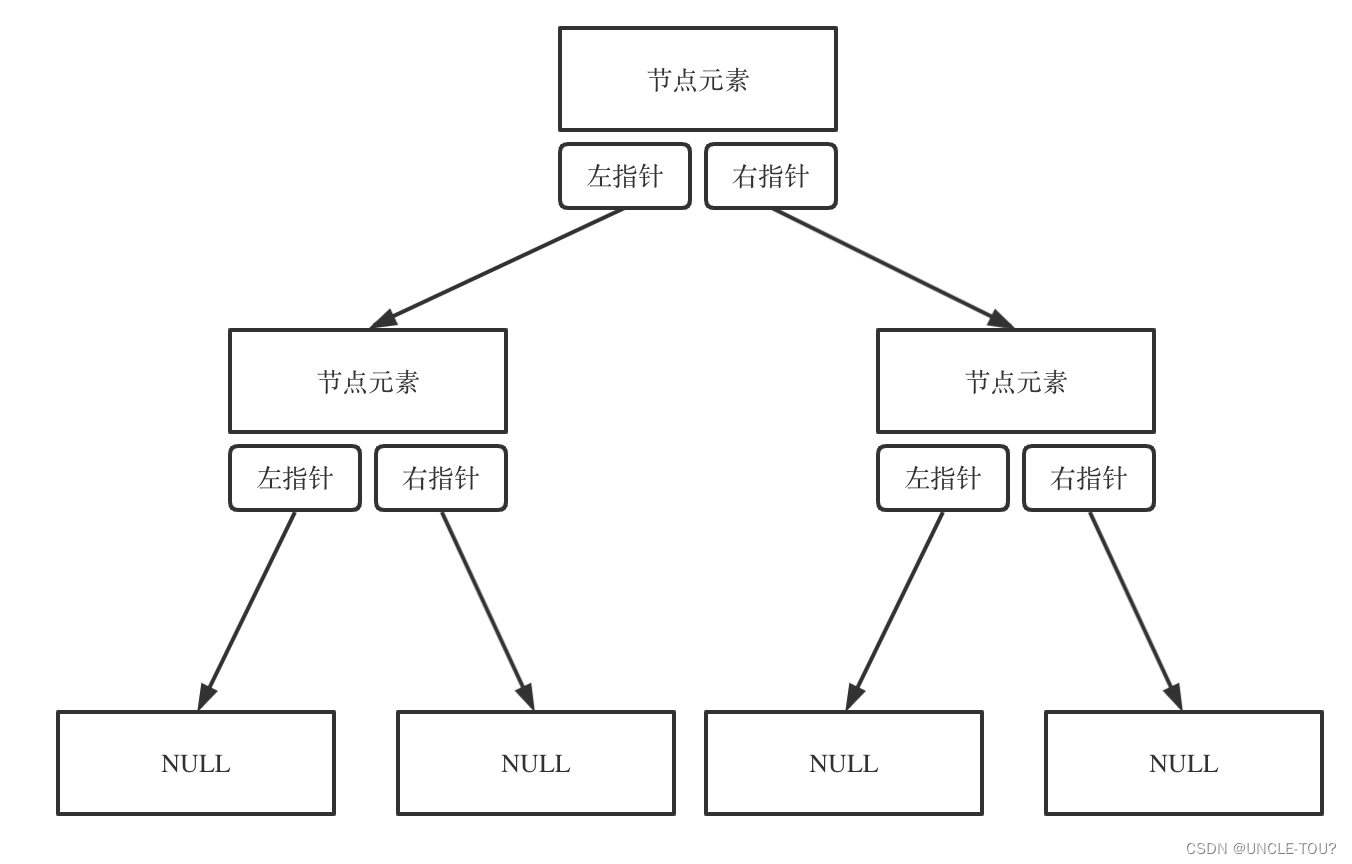
1.2 二叉树的存储

链式存储

用指针。一般用这个

顺序存储

用数组

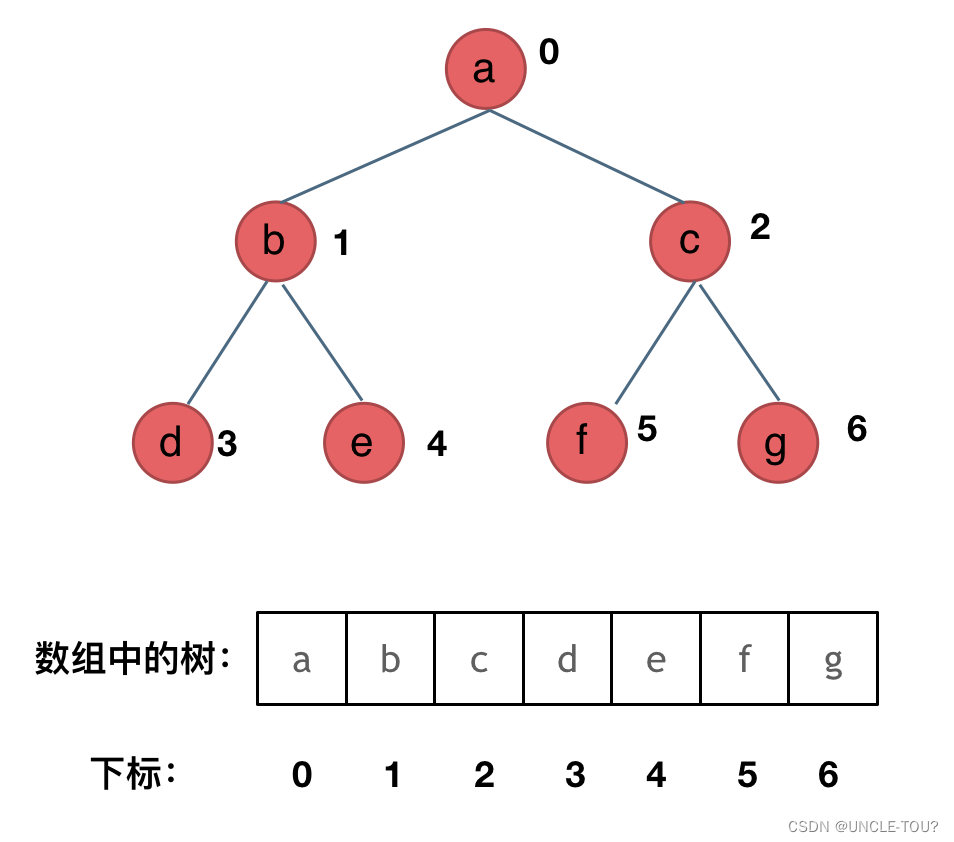
若父节点的数组下标为i，则左子节点下标为2i+1，右子节点下标为2i+2。

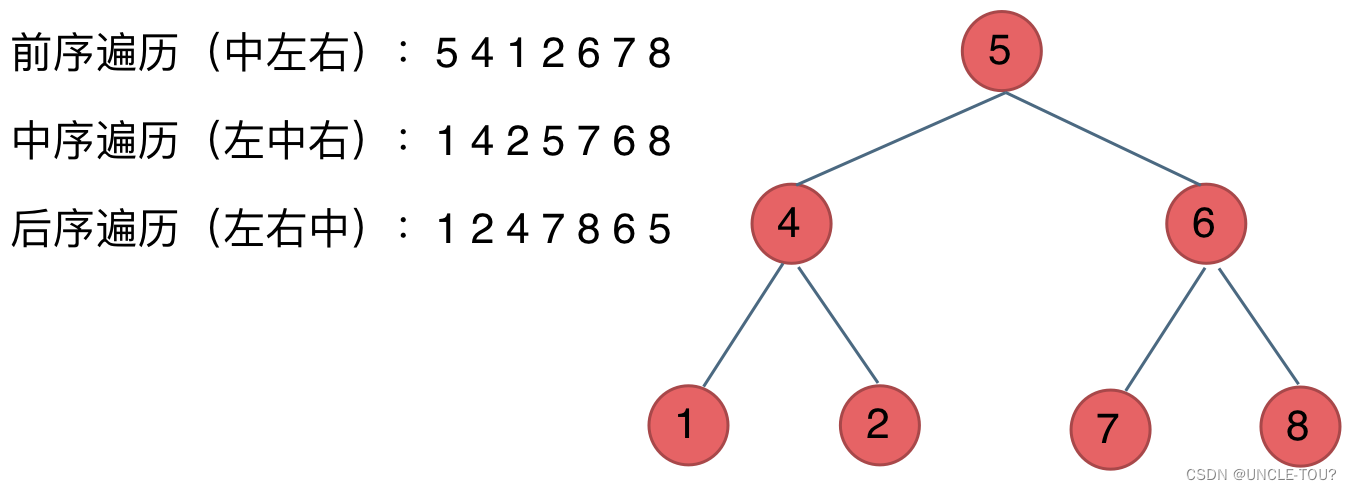
1.3 二叉树的遍历方式

深度优先遍历：往深里走，直到碰到叶子节点。
-前序遍历：中左右
-中序遍历：左中右
-后序遍历：左右中
广度优先遍历：一层一层走

python下的树定义：

class TreeNode:def __init__(self, val, left=None, right=None):self.val = val # 值self.left = left # 左指针self.right = right # 右指针

2 递归遍历

每次写递归要按照以下三要素来写：

1. 确定递归函数的参数和返回值。
2. 确定终止条件
3. 确定单层递归的逻辑

2.1 前序递归（中左右）

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def preorderTraversal(self, root: TreeNode) -> List[int]:res = []def dfs(node):if node is None:returnres.append(node.val)dfs(node.left)dfs(node.right)dfs(root)return res

2.1 中序递归（左中右）

class Solution:def inorderTraversal(self, root: TreeNode) -> List[int]:res = []def dfs(node):if node is None:returndfs(node.left)res.append(node.val)dfs(node.right)dfs(root)return res

2.3 后序递归（左右中）

class Solution:def postorderTraversal(self, root: TreeNode) -> List[int]:res = []def dfs(node):if node is None:returndfs(node.left)dfs(node.right)res.append(node.val)dfs(root)return res

3 迭代遍历

需要创建一个数组res用于保存结果，和一个栈stack用于保存当前节点。迭代中有两个操作：

1. 处理当前节点：将元素放入res中
2. 遍历节点

3.1 前序迭代遍历（中左右）

先将根节点压栈，然后右子节点压栈，然后左子节点压栈
注意：这里和中左右的顺序是相反的！因为这么做出栈的时候才是正确的顺序

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def preorderTraversal(self, root: TreeNode) -> List[int]:stack = [root]res = []if root == None:return reswhile stack: # 当栈非空时node = stack.pop()res.append(node.val) # 中结点先处理if node.right: # 右孩子先入栈stack.append(node.right)if node.left:  # 左孩子后入栈stack.append(node.left)return res

3.2 中序迭代遍历（左中右）

中序迭代遍历的代码不与前序的通用，因为处理顺序和访问顺序不一样。

class Solution:def inorderTraversal(self, root: TreeNode) -> List[int]:res = []stack = [] # 不能提前将root放入stackcur = root # 当前节点if root == None:return reswhile cur or stack: # 当当前节点和栈有一个非空时if cur != None:stack.append(cur)cur = cur.left  # 先一直靠左深入else: # 当左边走到头了，处理栈顶节点cur = stack.pop()res.append(cur.val) # 中cur = cur.right # 右return res

3.3 后序迭代遍历（左右中）

调整前序遍历的顺序即可，将res反转。
注意，反转前res的顺序为中右左，因此入栈的顺序应该左孩子先入栈，右孩子后入栈。

class Solution:def postorderTraversal(self, root: TreeNode) -> List[int]:res = []stack = [root]if root == None:return reswhile stack:node = stack.pop()res.append(node.val)if node.left:stack.append(node.left)# 左孩子先入栈if node.right:stack.append(node.right)# 右孩子后入栈return res[::-1] #反转

4 统一迭代

其实针对三种遍历方式，使用迭代法是可以写出统一风格的代码。
就将访问的节点放入栈中，把要处理的节点也放入栈中但是要做标记。要处理的节点放入栈之后，紧接着放入一个空指针作为标记。

4.1 前序遍历（中左右）

class Solution:def preorderTraversal(self, root: TreeNode) -> List[int]:res = []stack = [root]if root == None:return reswhile stack:if node != None:if node.right:stack.append(node.right)if node.left:stack.append(node.left)stack.append(node) # 把访问的节点和要处理的节点都入栈stack.append(None) # 并且在要处理的节点之后添加一个空值else:node = stack.pop()res.append(node.val)return res

4.2 中序遍历（左中右）

class Solution:def inorderTraversal(self, root: TreeNode) -> List[int]:res = []stack = [root]if root == None:return reswhile stack:node = stack.pop()if node != None:if node.right:stack.append(node.right)stack.append(node)stack.append(None)if node.left:stack.append(node.left)else:node = stack.pop()res.append(node.val)return res

4.3 后序遍历（左右中）

class Solution:def postorderTraversal(self, root: TreeNode) -> List[int]:res = []stack = [root]if root == None:return reswhile stack:node = stack.pop()if node != None:stack.append(node)stack.append(None)if node.right != None:stack.append(node.right)if node.left != None:stack.append(node.left)else:node = stack.pop()res.append(node.val)return res