Dilworth 定理
这是一个关于偏序集的定理,事实上它也可以扩展到图论,dp等中,是一个很有意思的东西
偏序集
偏序集是由集合 S S S以及其上的一个偏序关系 R R R定义的,记为 ( S , R ) (S,R) (S,R)
偏序关系:
对于一个二元关系 R ⊂ S × S R\subset S\times S R⊂S×S,如果其满足:
- ∀ x ∈ S , x R x \forall x\in S,xRx ∀x∈S,xRx 自反性
- ∀ x , y ∈ S \forall x,y\in S ∀x,y∈S,若 x R y xRy xRy且 y R x yRx yRx,则 x = y x=y x=y 反对称性
- x R y , y R z → x R z xRy,yRz\rightarrow xRz xRy,yRz→xRz 传递性
显然自然数集 N N N以及最常见的小于等于关系 ≤ \leq ≤, ( N , ≤ ) (N,\leq) (N,≤)就构成了一个偏序集
事实上 ( N ∗ , ∣ ) (N^*,|) (N∗,∣)也是一个偏序集,其中 ∣ | ∣表示正整数的整除关系
以下为了讨论方便,我们将 R R R简记为 ≤ \leq ≤,当然它可以指代小于等于关系之外的其它关系
此外, ∀ x , y ∈ S \forall x,y\in S ∀x,y∈S,如果 x ≤ y x\leq y x≤y或 y ≤ x y\leq x y≤x,那么我们就说它们是可比的,否则说它们是不可比的
定义完了偏序集,我们可以从图上来看看它具体的样子
哈斯图(Hasse 图)
考虑一个偏序集 ( S , ≤ ) (S,\leq) (S,≤), ∀ x , y ∈ S \forall x,y\in S ∀x,y∈S,如果 x ≤ y x\leq y x≤y且不存在 z S . T . x ≤ z ≤ y z\ S.T. \ x\leq z\leq y z S.T. x≤z≤y,我们称为 y y y覆盖 x x x,那么此时我们就连一条从 x x x指向 y y y的有向边,最后得到的图就称为这个偏序集 ( S , ≤ ) (S,\leq) (S,≤)的Hasse图
比如下图是 x , y , z {x,y,z} x,y,z的幂集关于包含关系得到的Hasse图
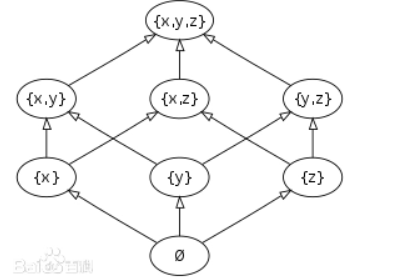
由于偏序关系满足了反对称性,所以Hasse图里面一定没有自环(否则就会合并成一个点),所以我们可以说Hasse图一定是一张DAG
其它偏序集的前置芝士
还是记我们要讨论的偏序集为 ( S , ≤ ) (S,\leq) (S,≤)
链:
偏序集中的一个全序子集。形式化地说,若集合 C ⊂ S C\subset S C⊂S,且 ∀ a , b ∈ C \forall a,b\in C ∀a,b∈C, a , b a,b a,b是可比的,那么 C C C就是 S S S的一个链
链这个名字起的就很有水平,因为我们不难发现,偏序集中的一个全序子集,其在Hasse图中似乎就一定表现为一条链。比如上图中的 { { x , y , z } , { x , z } , { x } , { ϕ } } \{\{x,y,z\},\{x,z\},\{x\},\{\phi\}\} {{x,y,z},{x,z},{x},{ϕ}}就是一个全序子集,在图中刚好也表现成一条链。但我没有严格证明,这边搁置。
类似地,我们定义一个反链
反链:
若集合 C ⊂ S C\subset S C⊂S,且 ∀ a , b ∈ C \forall a,b\in C ∀a,b∈C, a , b a,b a,b是不可比的,那么 C C C就是 S S S的一个反链
在图上看的话, { { x } , { y } , { z } } \{\{x\},\{y\},\{z\}\} {{x},{y},{z}}就是一个反链
深度:
最长链大小
宽度:
最长反链大小
以上两个定义也是相当的形象。因为我们不难发现,如果把Hasse图按照偏序关系从低到高排列的话,链在图中往往就是一条竖着的,而反链是横着的,由此给出如上定义
最小链划分:
将集合 S S S划分为最少的若干个不相交的链
最小反链划分:
将集合 S S S划分为最少的若干个不相交的反链
Dilworth 定理
现在可以给出Dilworth 定理的具体内容了
Lemma1 对于任意有限偏序集,其最长反链大小必等于最小链划分中链的数目
其对偶形式也成立:
Lemma2 对于任意有限偏序集,其最长链大小必等于其最小反链划分中反链的数目
以下讨论均假定偏序集有限
总结以下:
最小链划分 = 最长反链大小 = 偏序集宽度
最小反链划分 = 最长链大小 = 偏序集深度
先来证Lemma2:
记定理中的最长链大小为n,我们对n做数学归纳法
显然n=1时定理成立
若n=k时定理成立,我们来证 n=k+1时定理成立
此时偏序集中的最长链长度为k+1,我们取出集合 S S S的所有极大元,组成集合 M M M,显然 M M M是一个反链,并且考虑 S − M S-M S−M,其最大链长一定为k(因为取出了所有的极大元),根据之前的归纳假设, S − M S-M S−M的最小反链划分数目为 k,再加上M自己是一个反链,从而此时S的最小反链划分数为 k+1 = 最长链长度 □ \square □
再来看Lemma1:
考虑偏序集 ( S , ≤ ) (S,\leq) (S,≤),记 ∣ S ∣ = m |S|=m ∣S∣=m,我们对m进行归纳
m = 1 m=1 m=1时Lemma1显然成立
若 m = k m=k m=k时定理成立,我们来证 m = k + 1 m=k+1 m=k+1时定理成立:
设 A A A是集合 S S S的一条最长反链,记为
A = { a 1 , a 2 , . . . a w } A = \{a_1,a_2,...a_w\} A={a1,a2,...aw}
其中 ∣ A ∣ = w |A|=w ∣A∣=w
我们取
D ( A ) = { x ∉ A ∣ ∃ α ∈ S , x ≤ a } D(A) = \{x\notin A|\exists \alpha \in S,x\leq a\} D(A)={x∈/A∣∃α∈S,x≤a}
U ( A ) = { x ∉ A ∣ ∃ α ∈ S , a ≤ x } U(A) = \{x\notin A|\exists \alpha \in S,a\leq x\} U(A)={x∈/A∣∃α∈S,a≤x}
显然 D ( A ) ⋃ U ( A ) ⋃ A = S D(A)\bigcup U(A)\bigcup A = S D(A)⋃U(A)⋃A=S
若存在最长反链 A A A使得 D ( A ) , U ( A ) D(A),U(A) D(A),U(A)均非空:
A A A是 S S S的最长反链,故 A A A也是 A ⋃ D ( A ) A\bigcup D(A) A⋃D(A)的一个最长反链。注意到 ∣ U ( A ) ∣ ≥ 1 |U(A)|\geq 1 ∣U(A)∣≥1,故 ∣ A ⋃ D ( A ) ∣ ≤ k |A\bigcup D(A)|\leq k ∣A⋃D(A)∣≤k,从而由归纳假设, A ⋃ U ( A ) A\bigcup U(A) A⋃U(A)可以划分为 w w w条链 c 1 , c 2 , . . . c w c_1,c_2,...c_w c1,c2,...cw,其中 c i c_i ci的极大元是 a i a_i ai.(这一点显然)
同理, A ⋃ D ( A ) A\bigcup D(A) A⋃D(A)也可以划分为 w w w条链 d 1 , d 2 , . . . d w d_1,d_2,...d_w d1,d2,...dw,其中 d i d_i di的极小元是 a i a_i ai
从而,我们就可以将 S S S划分为 w w w条链: c 1 ∪ d 1 , . . . . c w ∪ d w c_1\cup d_1,....c_w\cup d_w c1∪d1,....cw∪dw
若对于任意最长反链 A A A,都有 D ( A ) = ϕ D(A)=\phi D(A)=ϕ或 U ( A ) = ϕ U(A)=\phi U(A)=ϕ
由假设,任一条反链 A A A必定构成全上界或者全下界。在 S S S中选一个极大元 y y y,再选一个极小元 x x x满足 x ≤ y x\leq y x≤y, { x , y } \{x,y\} {x,y}构成一条链 C C C,从而在集合 S − C S-C S−C中,任一条最长反链的大小为 w − 1 w-1 w−1(必定去除了一个元素),从而根据归纳假设, S − C S-C S−C的最小链划分数为 w − 1 w-1 w−1,再加上 C C C自己是一条链,故 S S S的最小链划分数为 w w w
□ \square □
应用举例
求一个序列的最大非递增序列长度以及其最少可以划分为多少个非递增序列
考虑由(位置,元素大小)这个二元组组成的集合,再定义一个偏序关系 < < <:
a < b a<b a<b当且仅当 a a a的位置< b b b的位置且 a a a的值 < b <b <b的值
从而这就构成了一个偏序集 ( s , < ) (s,<) (s,<),并且要求的分别就是集合的最长反链以及最小反链划分数
第一个问题可以直接dp即可,第二个问题,根据Dilworth 定理,实际上就是求偏序集的最长链大小,实际上也就是序列的LIS,非常妙的一个转化。
与DAG
之前说过,Hasse图就是一个DAG,而反过来,我们将DAG的点作为集合 S S S的元素,将偏序关系 ≤ \leq ≤定义为点之间的可达性,就定义了一个偏序集 ( S , ≤ ) (S,\leq) (S,≤)
从而DAG上的最小可重路径覆盖(要求覆盖所有点)就等价于偏序集 ( S , ≤ ) (S,\leq) (S,≤)上的最小链覆盖
同理,将DAG上的有向边作为集合 T T T的元素,将偏序关系 ≤ ′ \leq' ≤′定义为边之间的可达性,就得到的另一个偏序集 ( T , ≤ ′ ) (T,\leq') (T,≤′)
从而DAG上的最小可重路径覆盖(要求覆盖所有边)就等价于偏序集 ( T , ≤ ′ ) (T,\leq') (T,≤′)上的最小链覆盖
Erdős–Szekeres 定理
含至少 r s + 1 rs+1 rs+1个元素的实数序列 { a } \{a\} {a}要么有一个长为 r + 1 r+1 r+1的不下降子序列,要么有一个长为 s + 1 s+1 s+1 的不上升子序列
Proof:
设序列长度为 n ≥ r s + 1 n\geq rs+1 n≥rs+1,定义偏序集 { ( i , a i ) } i = 1 n \{(i,a_i)\}_{i=1}^{n} {(i,ai)}i=1n,其上的偏序关系 ≤ \leq ≤定义为:
( i , a i ) ≤ ( j , a i ) ⇔ ( i ≤ j ∧ a i ≤ a j ) (i,a_i)\leq (j,a_i)\Leftrightarrow (i\leq j \ \wedge \ a_i\leq a_j) (i,ai)≤(j,ai)⇔(i≤j ∧ ai≤aj)
假设该偏序集的宽度 ≤ s \leq s ≤s,则由Dilllworth定理可知其最小链覆盖数 ≤ s \leq s ≤s,若这些链的长度都 ≤ r \leq r ≤r,则总元素数 ≤ r s < r s + 1 ≤ n \leq rs< rs+1\leq n ≤rs<rs+1≤n
矛盾。
□ \square □
相关文章:

Dilworth 定理
这是一个关于偏序集的定理,事实上它也可以扩展到图论,dp等中,是一个很有意思的东西 偏序集 偏序集是由集合 S S S以及其上的一个偏序关系 R R R定义的,记为 ( S , R ) (S,R) (S,R) 偏序关系: 对于一个二元关系 R ⊂…...
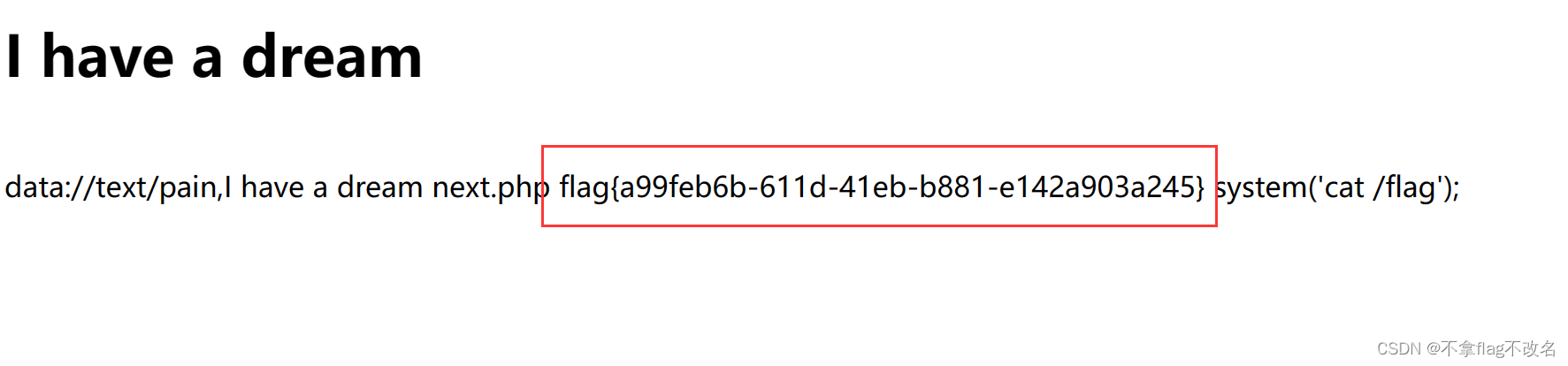
BUUCTF---web---[BJDCTF2020]ZJCTF,不过如此
1、点开连接,页面出现了提示 传入一个参数text,里面的内容要包括I have a dream。 构造:?/textI have a dream。发现页面没有显示。这里推测可能得使用伪协议 在文件包含那一行,我们看到了next.php的提示,我们尝试读取…...

力扣刷题---2206. 将数组划分成相等数对【简单】
题目描述🍗 给你一个整数数组 nums ,它包含 2 * n 个整数。 你需要将 nums 划分成 n 个数对,满足: 每个元素 只属于一个 数对。 同一数对中的元素 相等 。 如果可以将 nums 划分成 n 个数对,请你返回 true …...

2461. 长度为 K 子数组中的最大和(c++)
给你一个整数数组 nums 和一个整数 k 。请你从 nums 中满足下述条件的全部子数组中找出最大子数组和: 子数组的长度是 k,且子数组中的所有元素 各不相同 。 返回满足题面要求的最大子数组和。如果不存在子数组满足这些条件,返回 0 。 子数…...

range for
1. 基于范围的for循环语法 C11标准引入了基于范围的for循环特性,该特性隐藏了迭代器 的初始化和更新过程,让程序员只需要关心遍历对象本身,其语法也 比传统for循环简洁很多: for ( range_declaration : range_expression ) {loo…...

leetcode230 二叉搜索树中第K小的元素
题目 给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 个最小元素(从 1 开始计数)。 示例 输入:root [5,3,6,2,4,null,null,1], k 3 输出:3 解析 这道题应该是能做出…...
)
.Net Core学习笔记 框架特性(注入、配置)
注:直接学习的.Net Core 6,此版本有没有startup.cs相关的内容 项目Program.cs文件中 是定义项目加载 启动的地方 //通过builder对项目进行配置、服务的加载 var builder WebApplication.CreateBuilder(args); builder.Services.AddControllers();//将…...

利用AI技术做电商网赚,这些百万级赛道流量,你还不知道?!
大家好,我是向阳 AI技术的飞速扩展已经势不可挡,不管你承不承认,AI 已经毫无争议的在互联网中占有一席之地了 无论你是做内容产业的,还是做电商的,你现在都躲不开 AI。 现在互联网行业的竞争就是这么残酷 互联网行业…...

leetcode-560 和为k的数组
一、题目描述 给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的子数组的个数 。 子数组是数组中元素的连续非空序列。 注意:nums中的元素可为负数 输入:nums [1,1,1], k 2 输出:2输入:num…...

Spring Boot实战指南:从入门到企业级应用构建
目录 一、引言 二、快速入门 1. 使用Spring Initializr创建项目 三、Spring Boot基础概念与自动配置 1. 理解SpringBootApplication注解 2. 自动配置原理 3. 查看自动配置报告 四、Spring Boot核心特性及实战 1. 外部化配置 2. Actuator端点 3. 集成第三方库 五、Sp…...
OneAPI接入本地大模型+FastGPT调用本地大模型
将Ollama下载的本地大模型配置到OneAPI中,并通过FastGPT调用本地大模型完成对话。 OneAPI配置 新建令牌 新建渠道 FastGPT配置 配置docker-compose 配置令牌和OneAPI部署地址 配置config.json 配置调用的渠道名称和大模型名称 {"systemEnv": {&qu…...

Training-Free Consistent Text-to-Image Generation # 论文阅读
URL https://arxiv.org/pdf/2402.03286 TL;DR 2024 年 2 月 nvidia 的文章。提出了一种不需要任何额外训练的主体保持方法,可以一次生成的 batch 中,通过多个 prompt 生成对应的多张图片,这些图片都可以拥有一个主体。 本文提出的方法通过…...

Spring 中常用的手动装载 bean 方法
在 Spring 的 bean 装载条件中,虽然 Spring 给我们提供了非常好用便捷的 Condition 相关注解,但是很多时候 Condition 相关注解并不满足我们的需求,我需要更复杂的条件手动控制是否装置 bean。这个时候我们就可以实现 Spring 为我们提供的几个…...

如何合理设置Java线程池大小
如何合理设置Java线程池大小:依据任务类型定制策略 Java线程池的合理配置直接关系到系统性能和资源利用率。根据任务性质的不同,合理的线程池大小设置策略也有所区别,主要包括CPU密集型、IO密集型及混合型任务。 1. CPU密集型任务 特点&am…...

python3 pandas
pandas - Python Data Analysis Library...

【B站 heima】小兔鲜Vue3 项目学习笔记Day02
文章目录 Pinia1.使用2. pinia-计数器案例3. getters实现4. 异步action5. storeToRefsx 数据解构保持响应式6. pinia 调试 项目起步1.项目初始化和git管理2. 使用ElementPlus3. ElementPlus 主题色定制4. axios 基础配置5. 路由设计6. 静态资源初始化和 Error lens安装7.scss自…...

RedisTemplate 实现基于 Value 操作的简易锁机制
在高并发场景下,确保操作的原子性和避免竞态条件至关重要。Redis 提供了丰富的数据结构和操作,是实现分布式锁的一个高效选择。本文将介绍如何使用 RedisTemplate 的 opsForValue().setIfAbsent() 方法来实现一种简单的锁机制,并提供一个示例…...
其它高阶数据结构⑦_Skiplist跳表_概念+实现+对比
目录 1. Skiplist跳表的概念 2. Skiplist跳表的效率 3. Skiplist跳表的实现 3.1 力扣1206. 设计跳表 3.2 Skiplist的初始化和查找 3.3 Skiplist的增加和删除 3.4 Skiplist的源码和OJ测试 4. 跳表和平衡搜索树/哈希表的对比 本篇完。 1. Skiplist跳表的概念 skiplist是…...

力扣230. 二叉搜索树中第K小的元素
Problem: 230. 二叉搜索树中第K小的元素 文章目录 题目描述思路复杂度Code 题目描述 思路 直接利用二叉搜索树中序遍历为一个有序序列的特性: 记录一个int变量rank,在中序遍历时若当前rank k则返回当前节点值 复杂度 时间复杂度: O ( n ) O(n) O(n);其…...

Linux_应用篇(07) 系统信息与系统资源
在应用程序当中,有时往往需要去获取到一些系统相关的信息,譬如时间、日期、以及其它一些系统相关信息,本章将向大家介绍如何通过 Linux 系统调用或 C 库函数获取系统信息, 譬如获取系统时间、日期以及设置系统时间、日期等&#x…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...
