KNN及降维预处理方法LDA|PCA|MDS
文章目录
- 基本原理
- 模型介绍
- 模型分析
- python代码实现
- 降维处理
- 维数灾难 curse of dimensionality
- 线性变换 Linear Transformation
- LDA - 线性判别分析
- LDA python 实现
- PCA - 主成分分析
- PCA最近重构性
- PCA最大可分性
- PCA求解及说明
- PCA python实现
- 多维缩放 Multiple Dimensional Scaling
- R代码实现
基本原理
模型介绍
knn是一种监督式学习方法
其工作机制十分简单:给定测试样本,基于某种距离度量找出训练集中与其最靠近的k个样本,然后基于这k个临近点的信息来进行该测试样本所属类别的预测。
通常而言,在分类任务中一般使用“投票法”,即选择k个样本中出现最多的类别标记作为输出结果;
在回归任务中一般使用“平均法”,即将这k个样本的实际值的平均值作为输出结果
模型分析
作为一种监督式学习模型,knn不存在显式的模型训练过程
也就是说,在训练阶段我们只需要把样本保存起来,训练时间开销几乎为0
在机器学习中,这种模式又被称为"懒惰学习"
python代码实现
python sklearn neighbors包下包含了全部knn及其拓展算法的实现
KNeighborsClassifier中比较重要的超参数有:
- n_neighbors 表示k值
- weights “uniform”|“distance” 表示进行投票时每个数据点的权值
- metric “minkowski”
- p 2 二者共同定义距离计算公式式欧氏距离,即闵氏距离p=2的情况
import numpy as np
import pandas as pd
import warnings
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.neighbors import KNeighborsClassifierwarnings.filterwarnings("ignore")
iris_x, iris_y = load_iris(return_X_y=True)
# 为了可视化方便,我们只取iris中的前两个属性
iris_x = iris_x[:,:2]
x_train, x_test, y_train, y_test \= train_test_split(iris_x,iris_y,test_size=0.2,random_state=42)
knn_clf = KNeighborsClassifier(n_neighbors=7)
knn_clf.fit(x_train,y_train)
y_pred = knn_clf.predict(x_test)
import matplotlib as mpl
from matplotlib import pyplot as plt%matplotlib inline
mpl.rcParams["font.sans-serif"] = "SimHei"
fig,ax = plt.subplots(1,3,figsize=(12,4),facecolor="whitesmoke",edgecolor="gray")
class0 = []
class1 = []
class2 = []
for idx,cls in enumerate(iris_y):if cls == 0:class0.append(iris_x[idx,:])elif cls == 1:class1.append(iris_x[idx,:])else:class2.append(iris_x[idx,:])
ax[0].set_title("original dataset class")
ax[0].scatter(np.asarray(class0)[:,0],np.asarray(class0)[:,1],marker="*",color="r",s=3,label="class0")
ax[0].scatter(np.asarray(class1)[:,0],np.asarray(class1)[:,1],marker="*",color="orange",s=3,label="class0")
ax[0].scatter(np.asarray(class2)[:,0],np.asarray(class2)[:,1],marker="*",color="purple",s=3,label="class0")
ax[0].legend(loc="upper right")
ax[0].set_ylim([2.0,4.5])
ax[0].set_xlim([4.0,8.0])class0_pred = []
class1_pred = []
class2_pred = []
for idx,cls in enumerate(y_pred):if cls == 0:class0_pred.append(x_test[idx,:])elif cls == 1:class1_pred.append(x_test[idx,:])else:class2_pred.append(x_test[idx,:])
ax[1].set_title("original test dataset class")
ax[1].scatter(np.asarray(class0_pred)[:,0],np.asarray(class0_pred)[:,1],marker="*",color="r",s=3,label="class0")
ax[1].scatter(np.asarray(class1_pred)[:,0],np.asarray(class1_pred)[:,1],marker="*",color="orange",s=3,label="class0")
ax[1].scatter(np.asarray(class2_pred)[:,0],np.asarray(class2_pred)[:,1],marker="*",color="purple",s=3,label="class0")
ax[1].legend(loc="upper right")
ax[1].set_ylim([2.0,4.5])
ax[1].set_xlim([4.0,8.0])class0_test = []
class1_test = []
class2_test = []
for idx,cls in enumerate(y_test):if cls == 0:class0_test.append(x_test[idx,:])elif cls == 1:class1_test.append(x_test[idx,:])else:class2_test.append(x_test[idx,:])
ax[2].set_title("predict test dataset class")
ax[2].scatter(np.asarray(class0_test)[:,0],np.asarray(class0_test)[:,1],marker="*",color="r",s=3,label="class0")
ax[2].scatter(np.asarray(class1_test)[:,0],np.asarray(class1_test)[:,1],marker="*",color="orange",s=3,label="class0")
ax[2].scatter(np.asarray(class2_test)[:,0],np.asarray(class2_test)[:,1],marker="*",color="purple",s=3,label="class0")
ax[2].legend(loc="upper right")
ax[2].set_ylim([2.0,4.5])
ax[2].set_xlim([4.0,8.0])
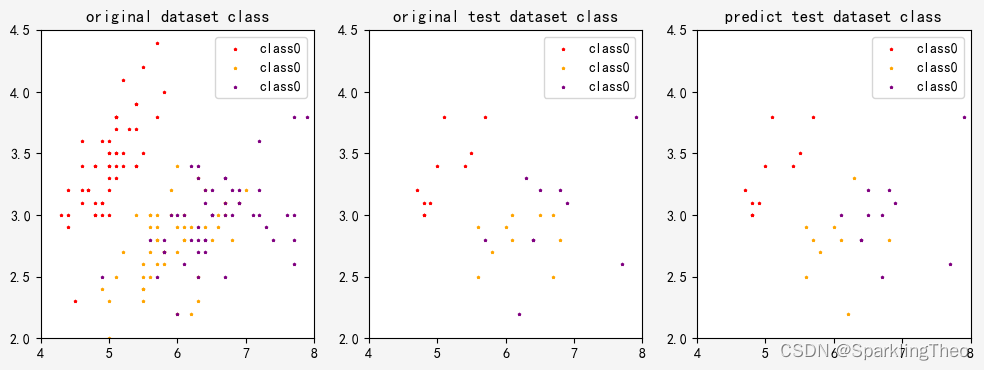
可以看出,knn存在一定的分类误差,我们可以通过调节k的数量来使模型更精确,下面计算模型精确度:
accuracy = accuracy_score(y_pred, y_test)
$ accuracy 0.7666666666666667
降维处理
维数灾难 curse of dimensionality
经过极差对所有维度进行标准化变换后,我们可以将n个样本点视为p维单位超立方体中均匀分布的n个点
Bellman研究表明,假设样本点 X 0 X_0 X0处于超立方体的一个顶点位置,找到他的近邻比率 r r r(近邻数量占全部数据量的比值)时超立方体各边的期望边界长度为
E d p ( r ) = r 1 p Ed_p(r) = r^{\frac{1}{p}} Edp(r)=rp1
也就是说,对于一个 p = 10 p=10 p=10的10维空间而言,要找到 r = 0.01 r=0.01 r=0.01或者 r = 0.1 r=0.1 r=0.1的近邻, E d ( 0.01 ) = 0.0 1 1 10 = 0.63 Ed(0.01)=0.01^{\frac{1}{10}}=0.63 Ed(0.01)=0.01101=0.63和 E d ( 0.1 ) = 0. 1 1 10 = 0.8 Ed(0.1)=0.1^{\frac{1}{10}}=0.8 Ed(0.1)=0.1101=0.8,计算结果表明取值距离跨越了总长度的 63 % 63\% 63%和 80 % 80\% 80%
与此同时,单纯减少r的量值也不能够对超立方体各边界期望长度的减少做出多大贡献,但是同时会增大预测的方差
以上推导从一个侧面证明当维度增高时,数据点在高维度空间中的分布将不再平均,它们将更多集中在空间的边缘位置,从而导致算法的开销明显增大
下面我们将介绍两种降维的思路,其一是基于线性变化的思想,另一种则是利用低维嵌入的思想
线性变换 Linear Transformation
一般来说,最简单的维度变换即为对原始高维空间进行线性变换,给定d维空间中的样本
X = { x 1 , x 1 , ⋯ , x m } \mathbf{X}=\{\mathbf{x_1},\mathbf{x_1},\cdots,\mathbf{x_m}\} X={x1,x1,⋯,xm}
变换后得到 d ′ < d d^{\prime}<d d′<d维空间中的样本
Z = W T X Z = W^TX Z=WTX
其中 W ∈ R d × d ′ W\in \mathbb{R}^{d\times d^\prime} W∈Rd×d′是变换矩阵, Z ∈ R d ′ × m Z\in \mathbb{R}^{d^\prime \times m} Z∈Rd′×m是样本在新空间中的表达
接下来,我们根据变换后对于低维子空间性质的不同要求可以构造出相应的最优化问题,并对 W W W施加不同约束,
最常见的线性变换包括LDA以及PCA
LDA - 线性判别分析
传统的LDA是二分类线性判别模型,属于有监督学习的范畴,放在这里是因为我们的确使用到了线性变换的模型思路
与此同时,我们可以通过OVO或是OVR的组合模式将该二分类模型扩展至多分类模型之中
在该线性变换模型中,我们将对高维空间( n n n维)中的数据点投影到 n − 1 n-1 n−1维度的超平面上,投影后的点将按照类别进行区分
相应的约束条件是:投影后类内方差最小,类间方差最大
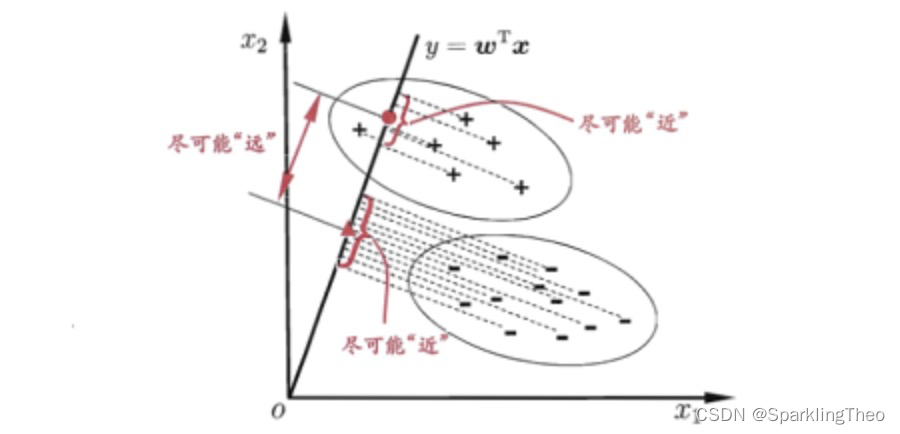
- LDA二维示意图【实际上可能有多维】,其中“+”和“-”分别代表正例和反例
首先,我们定义数据集中的主要变量
给定数据集
D = { ( x i , y i ) } i = 1 m , y i ∈ ( 0 , 1 ) D=\{(x_i,y_i)\}^{m}_{i=1}, y_i \in (0,1) D={(xi,yi)}i=1m,yi∈(0,1)
令 X i , μ i , Σ i X_i,\mu_i,\Sigma_i Xi,μi,Σi分别为第 i ∈ ( 0 , 1 ) i \in (0,1) i∈(0,1)类实例的集合、均值向量和协方差矩阵
若将数据投影到直线 ω \mathbf{\omega} ω上,我们可以分别得出两类样本均值和协方差矩阵的投影分别为
ω T μ 0 , ω T μ 1 , ω T Σ 0 ω , ω T Σ 1 ω \mathbf{\omega}^T\mathbf{\mu_0},\mathbf{\omega}^T\mathbf{\mu_1},\mathbf{\omega}^T\mathbf{\Sigma_0}\mathbf{\omega},\mathbf{\omega}^T\mathbf{\Sigma_1}\mathbf{\omega} ωTμ0,ωTμ1,ωTΣ0ω,ωTΣ1ω
欲使得同类样本投影点尽可能接近,即同类样本投影点的协方差尽可能小,我们需要
ω T Σ 0 ω + ω T Σ 1 ω \mathbf{\omega}^T\mathbf{\Sigma_0}\mathbf{\omega}+ \mathbf{\omega}^T\mathbf{\Sigma_1}\mathbf{\omega} ωTΣ0ω+ωTΣ1ω
尽可能小
欲使得异类样本投影点尽可能远离,即类中心之间距离尽可能大,我们需要
∣ ∣ ω T μ 0 − ω T μ 1 ∣ ∣ 2 2 ||\mathbf{\omega}^T\mathbf{\mu_0}-\mathbf{\omega}^T\mathbf{\mu_1}||^{2}_{2} ∣∣ωTμ0−ωTμ1∣∣22
尽可能大
同时考虑二者,我们可以通过比率的方法构造最优化问题的目标函数
J = ∣ ∣ ω T μ 0 − ω T μ 1 ∣ ∣ 2 2 ω T Σ 0 ω + ω T Σ 1 ω = ω T ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T ω ω T ( Σ 0 + Σ 1 ) ω \begin{array}{ll} J & = & \frac{||\mathbf{\omega}^T\mathbf{\mu_0}-\mathbf{\omega}^T\mathbf{\mu_1}||^{2}_{2}}{\mathbf{\omega}^T\mathbf{\Sigma_0}\mathbf{\omega}+ \mathbf{\omega}^T\mathbf{\Sigma_1}\mathbf{\omega}} \\ & = &\frac{\mathbf{\omega}^T(\mathbf{\mu_0}-\mathbf{\mu_1}){(\mathbf{\mu_0}-\mathbf{\mu_1})}^T\mathbf{\omega}}{\mathbf{\omega}^T(\mathbf{\Sigma_0}+\mathbf{\Sigma_1})\mathbf{\omega}} \end{array} J==ωTΣ0ω+ωTΣ1ω∣∣ωTμ0−ωTμ1∣∣22ωT(Σ0+Σ1)ωωT(μ0−μ1)(μ0−μ1)Tω
为了简化公式的书写,我们构造类内散度矩阵
S w = Σ 0 + Σ 1 S_w = \mathbf{\Sigma_0}+\mathbf{\Sigma_1} Sw=Σ0+Σ1
以及类间散度矩阵
S b = ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T S_b = (\mathbf{\mu_0}-\mathbf{\mu_1}){(\mathbf{\mu_0}-\mathbf{\mu_1})}^T Sb=(μ0−μ1)(μ0−μ1)T
则最优化问题目标函数可以重写为
J = ω T S b ω ω T S w ω J= \frac{\mathbf{\omega}^TS_b\mathbf{\omega}}{\mathbf{\omega}^TS_w\mathbf{\omega}} J=ωTSwωωTSbω
由于最优化问题目标函数都是 ω \mathbf{\omega} ω的二次项,这表明该问题与其长度无关
不失一般性,我们令分母 ω T S w ω = 1 \mathbf{\omega}^TS_w\mathbf{\omega}=1 ωTSwω=1,则最优化问题可以表述如下:
arg min ω − ω T S b ω s . t . ω T S w ω = 1 \begin{array}{ll} & \mathop{\arg\min}_{\omega} & -\mathbf{\omega}^TS_b\mathbf{\omega} \\ & s.t. & \mathbf{\omega}^TS_w\mathbf{\omega}=1 \end{array} argminωs.t.−ωTSbωωTSwω=1
求解该类最优化问题我们将使用拉格朗日乘子法配合KKT条件,这里不再赘述,最后得到分类直线方程为:
ω = S ω − 1 ( μ 0 − μ 1 ) \mathbf{\omega} = {S_{\omega}}^{-1}(\mathbf{\mu_0}-\mathbf{\mu_1}) ω=Sω−1(μ0−μ1)
LDA python 实现
python sklearn 包中 LinearDiscriminantAnalysis 提供LDA功能
import numpy as np
import pandas as pd
import warnings
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.metrics import accuracy_scorewarnings.filterwarnings("ignore")
iris_x, iris_y = load_iris(return_X_y=True)
iris_x.shape$(150,4)
可以看出,原始数据中我们拥有4个属性,也就是说降维之前我们的维度p=4
# 注意,由于受到svd影响,输出降维后的矩阵实际上是(属性值-1)和(类别值-1)二者之间的最小值
lda_model = LinearDiscriminantAnalysis(solver='svd')
lda_model.fit(iris_x,iris_y)
iris_transformed = lda_model.transform(iris_x)
iris_transformed.shape$(150,2)
使用LDA进行降维后,我们的属性来到了2个。当我们评价降维对模型带来的增益时,我们常常通过对模型本身的准确度提升来间接评价降维带来的优势
PCA - 主成分分析
主成分分析所要达到的主要目的在于能够使用一个低维的超平面更恰当的表达在高维中存在的各数据点
如何评价这样的超平面呢?我们有以下两种方式:
- 最近重构性: 样本点到这个超平面的距离足够近
- 最大可分性: 样本点在这个超平面上的投影能尽可能分开
有趣的是,基于以上两种判别标准,我们能够分别推导出PCA相同的最优化问题
PCA最近重构性
假定样本进行了中心化,即
∑ i x i = 0 \sum_{i}x_i = 0 i∑xi=0
同时假定投影变换后得到的新坐标系为:
{ ω 1 , ω 1 , ⋯ , ω d } \{\omega_1,\omega_1,\cdots,\omega_d\} {ω1,ω1,⋯,ωd}
其中 ω i \omega_i ωi是标准正交基向量,这意味着
{ ∣ ∣ ω i ∣ ∣ 2 = 1 ω i T ω j = 0 , ( i ≠ j ) \left \{ \begin{array}{ll} ||\omega_i||_2 = 1 \\ {\omega_i}^T{\omega_j} = 0, (i \ne j) \end{array} \right . {∣∣ωi∣∣2=1ωiTωj=0,(i=j)
PCA的目标是将维度降低到 d ′ < d d^{\prime}<d d′<d,那么样本点 x i x_i xi在低位坐标系中的投影为
z i = ( z i 1 , z i 2 , ⋯ , z i d ′ ) z_i=(z_{i1},z_{i2},\cdots,z_{id^\prime}) zi=(zi1,zi2,⋯,zid′)
其中 z i j = ω j T x i z_{ij}={\omega_j}^Tx_i zij=ωjTxi是 x i x_i xi在低维坐标系下第j维的坐标
若基于 z i z_i zi来重构 x i x_i xi,则会得到
x ^ i = ∑ j = 1 d ′ z i j ω j \hat x_i = \sum^{d^\prime}_{j=1}z_{ij}\omega_j x^i=j=1∑d′zijωj
那么,我们可以构造原样本点 x i x_i xi与基于地位样本点重构的样本点 x ^ i \hat x_i x^i之间的距离
∑ i = 1 m ∣ ∣ ∑ j = 1 d ′ z i j ω j − x i ∣ ∣ 2 2 = ∑ i = 1 m z i T z i − 2 ∑ i = 1 m z i T W T x i + c o n s t ∝ − t r ( W T ∑ i = 1 m z i T x i ) ∝ − t r ( W T ∑ i = 1 m ( W T x i ) T x i ) ∝ − t r ( W T ( ∑ i = 1 m x i x i T ) W ) \begin{array}{ll} \displaystyle\sum_{i=1}^{m}\lvert\lvert\displaystyle\sum_{j=1}^{d^\prime}z_{ij}\omega_j-x_i||^2_2 & = & \displaystyle\sum_{i=1}^{m}{z_i}^Tz_i - 2 \displaystyle\sum_{i=1}^{m}{z_i}^TW^Tx_i + const \\ & \propto & -tr(W^T\displaystyle\sum_{i=1}^{m}{z_i}^Tx_i) \\ & \propto & -tr(W^T\displaystyle\sum_{i=1}^{m}(W^Tx_i)^Tx_i) \\ & \propto & -tr(W^T(\displaystyle\sum_{i=1}^{m}x_i{x_i}^T)W) \end{array} i=1∑m∣∣j=1∑d′zijωj−xi∣∣22=∝∝∝i=1∑mziTzi−2i=1∑mziTWTxi+const−tr(WTi=1∑mziTxi)−tr(WTi=1∑m(WTxi)Txi)−tr(WT(i=1∑mxixiT)W)
其中, W W W是一个 ( d , d ′ ) (d,d^\prime) (d,d′)变换矩阵,根据最近重构性、也就是重构前后样本点距离相差最小原则,以上距离应当被构造成最优化问题中的最小化结构,
考虑到 ω i \omega_i ωi是标准正交基, ∑ i = 1 m x i x i T \displaystyle\sum_{i=1}^{m}x_i{x_i}^T i=1∑mxixiT是协方差矩阵,因此我们构造最优化问题如下:
arg min W − t r ( W T X X T W ) s . t . W T W = I \begin{array}{ll} \mathop{\arg\min}\limits_{W} & -tr(W^TX{X}^TW) \\ s.t. & W^TW = I \\ \end{array} Wargmins.t.−tr(WTXXTW)WTW=I
PCA最大可分性
从最大可分性出发,我们知道,投影后的样本点可以表示为 W T x i W^Tx_i WTxi,
若要求所有样本点在投影后能够尽可能分开,就要求投影后样本点之间的方差最大
投影哦呼样本点之间的方差为 ∑ i W T x i x i T W \sum_i W^Tx_i{x_i}^TW ∑iWTxixiTW,于是我们可以构造相应的优化问题如下:
arg max W t r ( W T X X T W ) s . t . W T W = I \begin{array}{ll} \mathop{\arg\max}\limits_{W} & tr(W^TX{X}^TW) \\ s.t. & W^TW = I \\ \end{array} Wargmaxs.t.tr(WTXXTW)WTW=I
PCA求解及说明
我们可以发现,两种方法得到的最优化问题是对偶的。
使用拉格朗日乘子法求解最优化问题,可得:
X X T ω i = λ i ω i XX^T\omega_i = \lambda_i\omega_i XXTωi=λiωi
接下来我们对 X X T XX^T XXT进行特征值分解,讲求的的特征值排序,取前 d ′ d^\prime d′个特征值对应的特征向量构成 W ∗ W^* W∗,该矩阵即为线性变换矩阵
但是我们需要注意的是,PCA模型的解释性是较低的,从另一种角度来说即为PCA降维后得到的特征是偏离原特征的实际价值的,我么只能从数学角度认为PCA处理后的特征能够更清晰地区分不同类别,但是不能够说明新生成的特征具备具体的物理意义。
PCA python实现
python sklearn decomposition.PCA 包提供PCA的相关操作
需要注意的是,PCA包中实际使用的是svd替代方阵的特征值分解,这样做的目的是减少计算开销并且尽可能小的影响精度
现在我们对sklearn.decomposition.PCA的主要参数做一个介绍:
- n_components:这个参数可以帮我们指定希望PCA降维后的特征维度数目。最常用的做法是直接指定降维到的维度数目,此时n_components是一个大于等于1的整数。当然,我们也可以指定主成分的方差和所占的最小比例阈值,让PCA类自己去根据样本特征方差来决定降维到的维度数,此时n_components是一个(0,1]之间的数。当然,我们还可以将参数设置为"mle", 此时PCA类会用MLE算法根据特征的方差分布情况自己去选择一定数量的主成分特征来降维。我们也可以用默认值,即不输入n_components,此时n_components=min(样本数,特征数)。
- whiten:判断是否进行白化。所谓白化,就是对降维后的数据的每个特征进行归一化,让方差都为1.对于PCA降维本身来说,一般不需要白化。如果你PCA降维后有后续的数据处理动作,可以考虑白化。默认值是False,即不进行白化。
- svd_solver:即指定奇异值分解SVD的方法,由于特征分解是奇异值分解SVD的一个特例,一般的PCA库都是基于SVD实现的。有4个可以选择的值:{‘auto’, ‘full’, ‘arpack’, ‘randomized’}。randomized一般适用于数据量大,数据维度多同时主成分数目比例又较低的PCA降维,它使用了一些加快SVD的随机算法。 full则是传统意义上的SVD,使用了scipy库对应的实现。arpack和randomized的适用场景类似,区别是randomized使用的是scikit-learn自己的SVD实现,而arpack直接使用了scipy库的sparse SVD实现。默认是auto,即PCA类会自己去在前面讲到的三种算法里面去权衡,选择一个合适的SVD算法来降维。一般来说,使用默认值就够了。
除了这些输入参数外,有两个PCA类的成员值得关注。第一个是explained_variance_,它代表降维后的各主成分的方差值。方差值越大,则说明越是重要的主成分。第二个是explained_variance_ratio_,它代表降维后的各主成分的方差值占总方差值的比例,这个比例越大,则越是重要的主成分
import numpy as np
import pandas as pd
import warnings
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_splitwarnings.filterwarnings("ignore")
iris_x, iris_y = load_iris(return_X_y=True)
iris_x.shape$(150,4)
pca = PCA(n_components=2)
iris_de = pca.fit_transform(iris_x)
iris_de.shape$(150,2)
多维缩放 Multiple Dimensional Scaling
多维缩放是另一种降维处理的思路,我们强调缩放前后向量的某种特性保持不变,
这种认识可以理解为我们只关心高维空间中某一个低维的分布,就好像这个低维分布是这个高维分布中的一个嵌入
因此,MDS追求原始空间中样本之间的距离在低维空间中得以保存
R代码实现
set.seed(42)
# prepare data
x1 <- runif(60,-1,1)
x2 <- runif(60,-1,1)
y <- sample(c(0,1),size=60,replace=TRUE, prob=c(0.3,0.7))
data <- data.frame(Fx1=x1, Fx2=x2, Fy=y)
# separate train and test set
sampleID <- sample(x=1:60,size=60*0.3)
x_test <- data[sampleID,]
x_train <- data[-sampleID,]
par(mfrow=c(2,2),mar=c(4,6,4,4))
plot(data[,1:2],pch=data[,3]+1,cex=0.8,xlab="x1",ylab="x2",main="total sample")
plot(x_train[,1:2],pch=x_train[,3]+1,cex=0.8,xlab="x1",ylab="x2",main="train and test sample")
points(x_test[,1:2],pch=x_test[,3]+16,col=2,cex=0.8)# use all data
err_ratio <- vector()
for(i in 1:30){knn_fit <- knn(train=data[,1:2],test=data[,1:2],cl=as.factor(data[,3]),k=i)cross_table <- table(data[,3],knn_fit)err_ratio <- c(err_ratio,(1-sum(diag(cross_table))/sum(cross_table))*100)
}
plot(err_ratio, type="l", xlab="number of K", ylab="error rate %", main="k and error rate",ylim=c(0,80),hold=TRUE)# offsetting method 旁置法
err_ratio_offset <- vector()
for(i in 1:30){knn_fit_offset <- knn(train=x_train[,1:2],test=x_test[,1:2],cl=as.factor(x_train[,3]),k=i)cross_table_offset <- table(x_test[,3],knn_fit_offset)err_ratio_offset <- c(err_ratio_offset, (1-sum(diag(cross_table_offset))/sum(cross_table_offset))*100)
}
lines(1:30,err_ratio_offset,lty=2,col=2)# cross validation 留一法
error_ratio_cv <- vector()
for(i in 1:30){knn_fit_cv <- knn.cv(train=data[,1:2],cl=as.factor(data[,3]),k=i)cross_table_cv <- table(data[,3],knn_fit_cv)error_ratio_cv <- c(error_ratio_cv,(1-sum(diag(cross_table_cv))/sum(cross_table_cv))*100)
}
lines(1:30,error_ratio_cv,lty=3,col=4)# knn regression 回归
set.seed(24)
x3 <- runif(60,-1,1)
x4 <- runif(60,-1,1)
y2 <- runif(60,10,20)
data_reg <- data.frame(Fx3=x3, Fx4=x4, Fy=y2)
sampleID <- sample(x=1:60, size=60*0.3)
x2_test <- data_reg[sampleID,]
x2_train <- data_reg[-sampleID,]mse_vector <- vector()
for(i in 1:30){knn_fit_reg <- knn(train=x2_train[,1:2],test=x2_test[,1:2],cl=x2_train[,3],k=i,prob=FALSE)# due to the fact that res of knn is a factor, # we need to change it back to numeric vectorknn_fit_reg <- as.double(as.vector(knn_fit_reg))mse <- sum((x2_test[,3]-knn_fit_reg)^2)/length(x2_test[,3])print((x2_test[,3]-knn_fit_reg)^2)print(mse)mse_vector <- c(mse_vector,mse)
}
plot(mse_vector,type="l", xlab="k", ylab="mse",main="k-mse relationship",ylim=c(0,80))
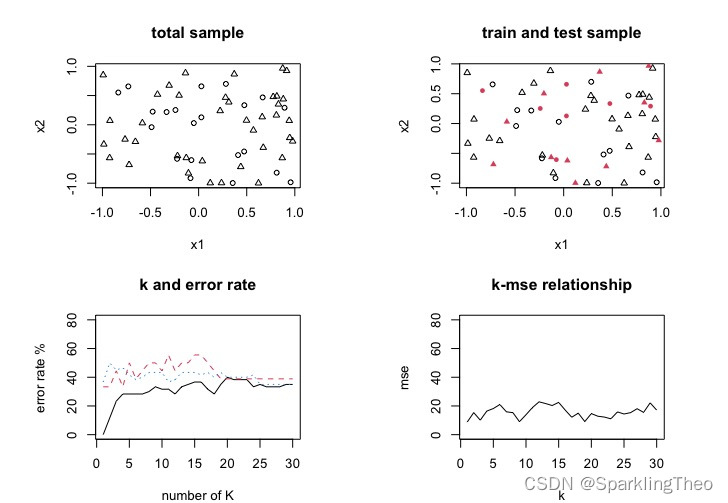
相关文章:

KNN及降维预处理方法LDA|PCA|MDS
文章目录 基本原理模型介绍模型分析 python代码实现降维处理维数灾难 curse of dimensionality线性变换 Linear TransformationLDA - 线性判别分析LDA python 实现PCA - 主成分分析PCA最近重构性PCA最大可分性PCA求解及说明PCA python实现 多维缩放 Multiple Dimensional Scali…...

论文精读-SwinIR Image Restoration Using Swin Transformer
论文精读-SwinIR: Image Restoration Using Swin Transformer SwinIR:使用 Swin Transformer进行图像恢复 参数量:SR 11.8M、JPEG压缩伪影 11.5M、去噪 12.0M 优点:1、提出了新的网络结构。它采用分块设计。包括浅层特征提取:cnn提取&#…...

解释Spring Bean的生命周期
Spring Bean的生命周期涉及到Bean的创建、配置、使用和销毁的各个阶段。理解这个生命周期对于编写高效的Spring应用和充分利用框架的功能非常重要。下面是Spring Bean生命周期的主要步骤: 1. 实例化Bean Spring容器首先将使用Bean的定义(无论是XML、注…...
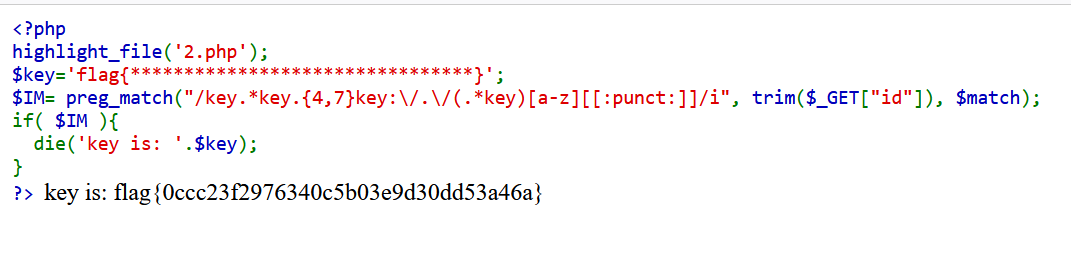
CTF网络安全大赛web题目:字符?正则?
题目来源于:bugku 题目难度:难 题目描 述: 字符?正则? 题目htmnl源代码: <code><span style"color: #000000"> <span style"color: #0000BB"><?php <br />highl…...
Linux——Docker容器虚拟化平台
安装docker 安装 Docker | Docker 从入门到实践https://vuepress.mirror.docker-practice.com/install/ 不需要设置防火墙 docker命令说明 docker images #查看所有本地主机的镜像 docker search 镜像名 #搜索镜像 docker pull 镜像名 [标签] #下载镜像&…...

Transformer详解(3)-多头自注意力机制
attention multi-head attention pytorch代码实现 import math import torch from torch import nn import torch.nn.functional as Fclass MultiHeadAttention(nn.Module):def __init__(self, heads8, d_model128, droput0.1):super().__init__()self.d_model d_model # 12…...

运用HTML、CSS设计Web网页——“西式甜品网”图例及代码
目录 一、效果展示图 二、设计分析 1.整体效果分析 2.头部header模块效果分析 3.导航及banner模块效果分析 4.分类classify模块效果分析 5.产品展示show模块效果分析 6.版权banquan模块效果分析 三、HTML、CSS代码分模块展示 1. 头部header模块代码 2.导航及bann…...

大语言模型是通用人工智能的实现路径吗?【文末有福利】
相关说明 这篇文章的大部分内容参考自我的新书《解构大语言模型:从线性回归到通用人工智能》,欢迎有兴趣的读者多多支持。 关于大语言模型的内容,推荐参考这个专栏。 内容大纲 相关说明一、哲学与人工智能二、内容简介三、书籍简介与福利粉…...

c语言——宏offsetof
1.介绍 !!! offsetof 是一个宏 2.使用举例 结构体章节的计算结构体占多少字节需要先掌握(本人博客结构体篇章中已经讲解过) 计算结构体中某变量相对于首地址的偏移,并给出说明 首先,结构体首个…...

C#串口通信-串口相关参数介绍
串口通讯(Serial Communication),是指外设和计算机间,通过数据信号线、地线等,按位进行传输数据的一种双向通讯方式。 串口是一种接口标准,它规定了接口的电气标准,没有规定接口插件电缆以及使用的通信协议,…...

节省时间与精力:用BAT文件和任务计划器自动执行重复任务
文章目录 1.BAT文件详解2. 经典BAT文件及使用场景3. 使用方法4. 如何设置BAT文件为定时任务5. 实例应用:自动清理临时文件 BAT文件,也就是批处理文件,是一种在Windows操作系统中自动执行一系列命令的文本文件。这些文件的扩展名为 .bat。通过…...

一年前的Java作业,模拟游戏玩家战斗
说明:一年前写的作业,感觉挺有意思的,将源码分享给大家。 刚开始看题也觉得很难,不过写着写着思路更加清晰,发现也没有想象中的那么难。 一、作业题目描述: 题目:模拟游戏玩家战斗 1.1 基础功…...

C++ 学习 关于引用
🙋本文主要讲讲C的引用 是基础入门篇~ 本文是阅读C Primer 第五版的笔记 🌈 关于引用 几个比较重要的点 🌿引用相当于为一个已经存在的对象所起的另外一个名字 🌞 定义引用时,程序把引用和它的初始值绑定(b…...
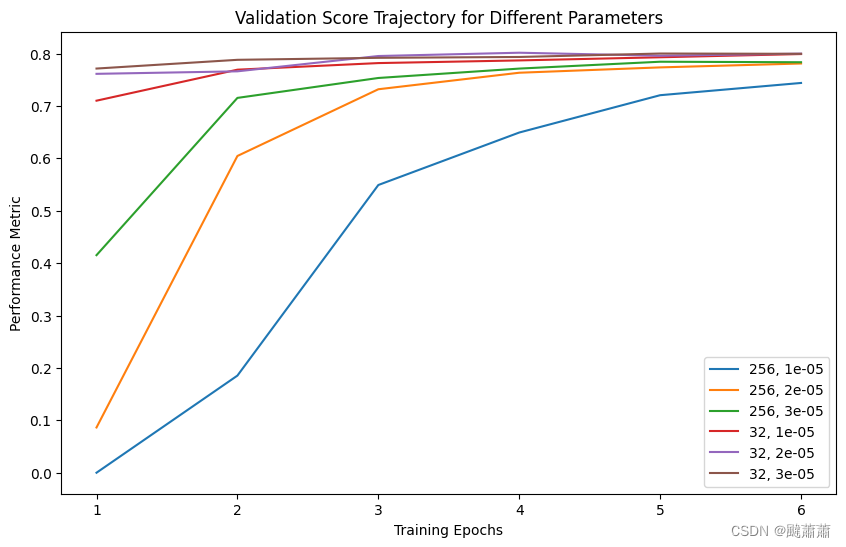
BERT ner 微调参数的选择
针对批大小和学习率的组合进行收敛速度测试,结论: 相同轮数的条件下,batchsize-32 相比 batchsize-256 的迭代步数越多,收敛更快批越大的话,学习率可以相对设得大一点 画图代码(deepseek生成)…...

【MySQL精通之路】系统变量-持久化系统变量
MySQL服务器维护用于配置其操作的系统变量。 系统变量可以具有影响整个服务器操作的全局值,也可以具有影响当前会话的会话值,或者两者兼而有之。 许多系统变量是动态的,可以在运行时使用SET语句进行更改,以影响当前服务器实例的…...

fdk-aac将aac格式转为pcm数据
int sampleRate 44100; // 采样率int sampleSizeInBits 16; // 采样位数,通常是16int channels 2; // 通道数,单声道为1,立体声为2FILE *m_fd NULL;FILE *m_fd2 NULL;HANDLE_AACDECODER decoder aacDecoder_Open(TT_MP4_ADTS, 1);if (!…...

【C语言深度解剖】(15):动态内存管理和柔性数组
🤡博客主页:醉竺 🥰本文专栏:《C语言深度解剖》 😻欢迎关注:感谢大家的点赞评论关注,祝您学有所成! ✨✨💜💛想要学习更多C语言深度解剖点击专栏链接查看&…...

力扣每日一题 5/25
题目: 给你一个下标从 0 开始、长度为 n 的整数数组 nums ,以及整数 indexDifference 和整数 valueDifference 。 你的任务是从范围 [0, n - 1] 内找出 2 个满足下述所有条件的下标 i 和 j : abs(i - j) > indexDifference 且abs(nums…...
无线电失控保护(一))
(1)无线电失控保护(一)
文章目录 前言 1 何时触发失控保护 2 将会发生什么 3 接收机配置...
基于51单片机的多功能万年历温度计—可显示农历
基于51单片机的万年历温度计 (仿真+程序+原理图+设计报告) 功能介绍 具体功能: 本设计基于STC89C52(与AT89S52、AT89C52通用,可任选)单片机以及DS1302时钟芯片、DS18B…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...
