【MATLAB源码-第214期】基于matlab的遗传算法GA最短路径路由优化算法仿真。
操作环境:
MATLAB 2022a
1、算法描述
在现代网络通信和路径规划领域,最短路径路由优化算法是一项关键技术。它涉及在给定的网络拓扑中寻找从源点到目标点的最短或成本最低的路径。近年来,遗传算法(GA)因其出色的全局搜索能力和易于与其他优化技术集成的特性,被广泛应用于路径优化问题。本文将系统地描述基于遗传算法的最短路径路由优化算法的原理、实现过程及其应用。
1. 遗传算法简介
遗传算法是模拟生物进化过程的一种搜索启发式算法,它通过模拟自然选择和遗传学原理来解决优化问题。算法开始时会随机生成一组可能的解(称为种群),然后通过选择、交叉(杂交)和变异等遗传操作对这些解进行迭代改进,以期望产生越来越好的解。
2. 最短路径问题定义
最短路径问题是图论中的一个经典问题,目标是找到图中两点之间的最短路径。这个问题可以表示为一个加权图,其中节点代表图中的点,边的权重代表从一个节点到另一个节点的成本或距离。
3. 遗传算法在最短路径问题中的应用
在遗传算法应用于最短路径问题中,通常包括以下步骤:
3.1 初始种群的生成
初始种群的生成是遗传算法的第一步。在路径问题中,每个个体(染色体)代表一条可能的路径。这些路径可以是随机生成的,也可以使用特定的启发式方法生成以确保路径的有效性。
3.2 适应度函数的定义
适应度函数用于评估种群中每个个体的适应度,即路径的优劣。在最短路径问题中,适应度通常是路径长度的倒数或成本的负值,因此路径越短,适应度越高。
3.3 遗传操作
- 选择:选择操作是基于个体的适应度,从当前种群中选出优良个体构成下一代。常用的选择方法包括轮盘赌选择、锦标赛选择等。
- 交叉:交叉是遗传算法中的重要环节,通过交叉操作可以产生新的个体。在路径问题中,交叉操作需要确保子代个体的有效性,即子代代表的仍然是有效路径。
- 变异:在路径问题中,变异操作可以通过随机改变路径中的某些节点来实现,以引入新的遗传多样性。
3.4 终止条件
算法的终止条件可以是达到最大迭代次数、适应度达到某个阈值或适应度长时间没有显著改进。
4. 算法优化与挑战
虽然遗传算法在路径优化问题中具有潜力,但也面临一些挑战,如如何保证路径的有效性、如何提高算法的收敛速度等。针对这些问题,研究者提出了多种改进策略,包括使用特定的交叉和变异策略、结合局部搜索方法等。
5. 应用实例
在实际应用中,基于遗传算法的最短路径路由优化算法已被用于多种场景,如城市交通网络、计算机网络、物流配送等领域。通过这些应用,遗传算法展示了其强大的优化能力和广泛的适用性。
6. 总结
基于遗传算法的最短路径路由优化不仅提供了一种有效解决路径优化问题的方法,还促进了遗传算法及其相关技术的发展和完善。随着计算能力的提高和算法技术的进步,预计未来这类算法将在更多实际问题中发挥更大的作用。
2、仿真结果演示



3、关键代码展示
略
4、MATLAB 源码获取
V
点击下方名片
相关文章:

【MATLAB源码-第214期】基于matlab的遗传算法GA最短路径路由优化算法仿真。
操作环境: MATLAB 2022a 1、算法描述 在现代网络通信和路径规划领域,最短路径路由优化算法是一项关键技术。它涉及在给定的网络拓扑中寻找从源点到目标点的最短或成本最低的路径。近年来,遗传算法(GA)因其出色的全局…...
顺序栈 链式栈)
数据结构(四)顺序栈 链式栈
一、概念 栈是一种先进后出的数据结构。FILO(firt in late out) 逻辑结构:线性结构 二、存储结构: (一) 顺序存储 顺序栈 基于一个数组配合一个栈顶"指针(数组下标)–top" 顺序栈的本质就是对…...

【linux】g++/gcc编译器
目录 背景知识 gcc如何完成 预处理(进行宏替换) 编译(生成汇编) 汇编(生成机器可识别代码) 链接(生成可执行文件或库文件) 在这里涉及到一个重要的概念:函数库 函数库一般分为静态库和动态库两…...

VBA批量合并带有图片、表格与文本框的Word
本文介绍基于VBA语言,对大量含有图片、文本框与表格的Word文档加以批量自动合并,并在每一次合并时添加分页符的方法。 在我们之前的文章基于Python中docx与docxcompose批量合并多个Word文档文件并逐一添加分页符(https://blog.csdn.net/zhebu…...
市面上前 11 名的 Android 数据恢复软件
Android数据恢复软件是恢复无意中删除的文件或文件夹的必要工具。该软件还将帮助您恢复丢失或损坏的信息。本文介绍提供数据备份和磁盘克隆选项的程序,这些选项有助于在Android设备上恢复文件的过程。 如果您正在寻找一种有效的方法来恢复图像,文档&…...

【数据结构与算法 | 基础篇】数组模拟栈
1. 前言 前文我们刚提及了如何用单向链表来模拟栈. 我们还可以用数组来模拟栈.使用栈顶指针top来进行栈顶的操作. 2. 数组模拟栈 (1). 栈接口 public interface stack<E> {//压栈boolean push(E value);//弹栈, 栈非空返回栈顶元素E pop();//返回栈顶元素, 但不弹栈E…...

css卡片横线100%宽度
所需样式: 横线不用border, 用单独一个div, 这样就不会影响父组件的padding <div class"pumpDetailView"><div class"pump_title_name"><span>{{ pumpInfo.pointname }}</span><divclass"point_state":style"…...

回溯大法总结
前言 本篇博客将分两步来进行,首先谈谈我对回溯法的理解,然后通过若干道题来进行讲解,最后总结 对回溯法的理解 回溯法可以看做蛮力法的升级版,它在解决问题时的每一步都尝试所有可能的选项,最终找出所以可行的方案…...

基于Android Studio图书管理,图书借阅系统
目录 项目介绍 图片展示 运行环境 获取方式 项目介绍 用户 书架:搜索书籍,查看书籍,借阅书籍,收藏书籍,借阅书籍必须在一个月之内还书; 我的:可以修改密码,退出登录ÿ…...

SCSS 基本使用详解
一、引言 SCSS 是 Sass(Syntactically Awesome Stylesheets)的其中一种语法,是一种预处理器脚本语言,能够扩展 CSS 的功能,使其更加强大和高效。SCSS 保留了 CSS 的原有语法,同时增加了变量、嵌套规则、混…...
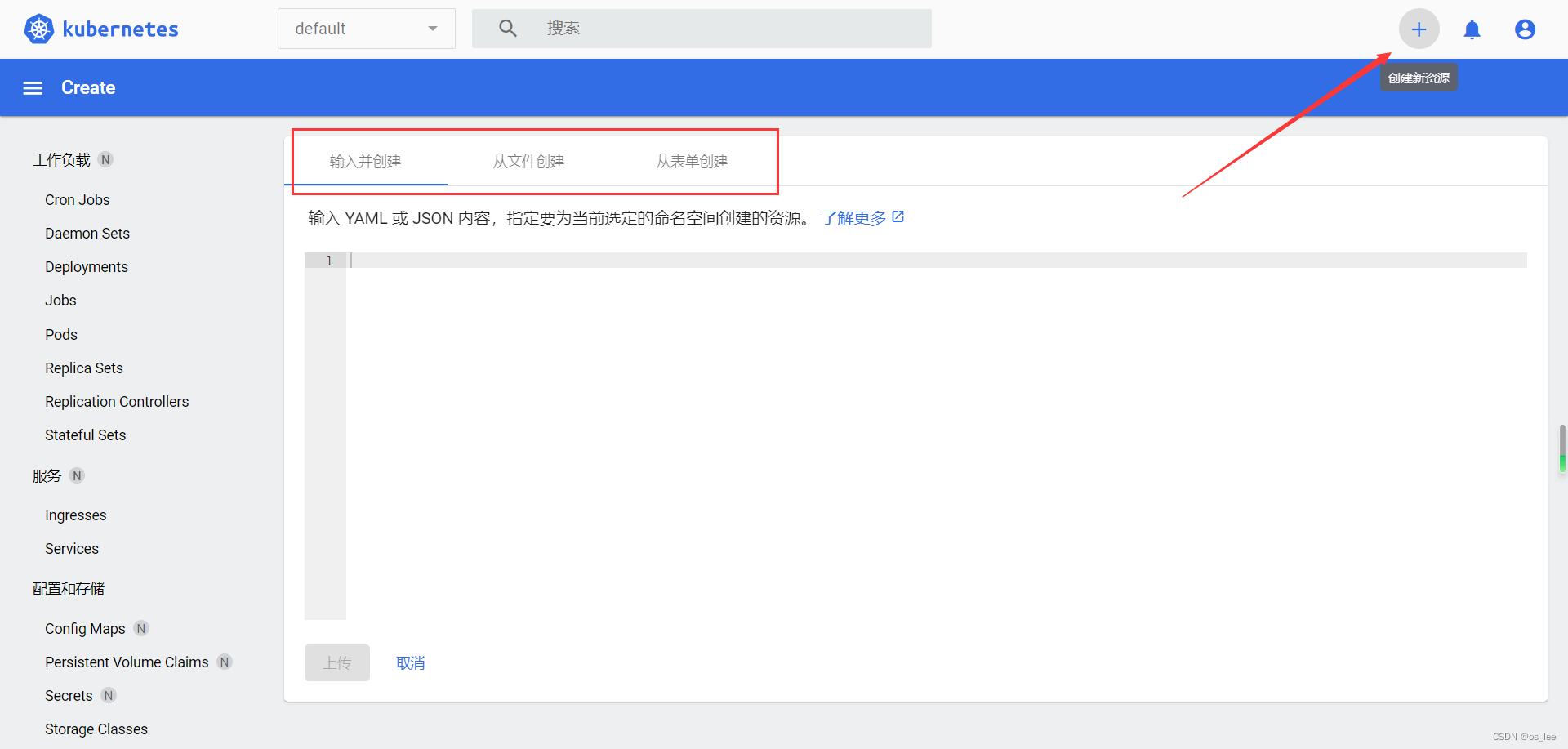
10.3.k8s的附加组件-图形化管理工具dashboard
目录 一、dashboard介绍 二、部署安装dashboard组件 1.下载dashboard本地文件 2.修改nodeport的端口范围 3.创建和查看dashboard 4.电脑浏览器访问测试 5.token登录方式登录dashboard 5.1.查看dashboard的token 5.2.继续查看用户token的secrets资源详细信息 5.3.复制…...
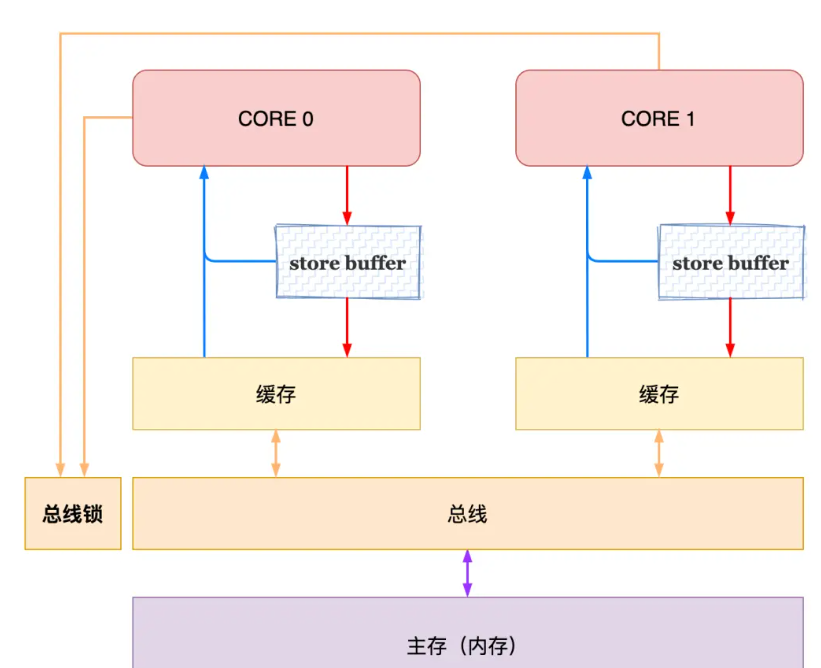
深入理解CPU缓存一致性
存储体系结构 速度快的存储硬件成本高、容量小,速度慢的成本低、容量大。为了权衡成本和速度,计算机存储分了很多层次,有寄存器、L1 cache、L2 cache、L3 cache、主存(内存)和硬盘等。 根据程序的空间局部性和时间局…...

python获取安装路径盘符
文章目录 一、前言二、实现方法一、前言 python写的客户端工具需要安装时,可以给用户一个默认的安装路径,如果直接写死个D、E、F盘什么的,那用户可能没有那个盘符,但是如果直接指定系统盘C盘,又不是那么友好,所以默认指定的安装路径应该尽量满足下面的要求: 盘符存在盘…...

CentOS 7.9安装NVIDIA P40显卡驱动、CUDA和cuDNN
文章目录 1、安装P40显卡驱动1.1 查看机器上有哪些显卡1.2 禁用nouveau1.3 安装依赖1.4 安装驱动 2、安装CUDA2.1 安装2.2 测试是否安装成功 3、安装cuDNN3.1 安装3.2 测试是否安装成功 4、总结 1、安装P40显卡驱动 1.1 查看机器上有哪些显卡 lspci | grep -i vga lspci | gr…...

SpringBoot多数据源启动出现循环依赖问题
在使用SpringBoot的项目中,如果是有使用多数据源,可能会存在启动时数据源循环依赖的报错,是因为使用了多数据源注入,和DataSourceAutoConfiguration数据源自动配置的DataSourceInitializerInvoker互相产生循环依赖导致。 这种错误…...
【一步一步了解Java系列】:何为数组,何为引用类型
看到这句话的时候证明:此刻你我都在努力加油陌生人个人主页:Gu Gu Study专栏:一步一步了解Java 喜欢的一句话: 常常会回顾努力的自己,所以要为自己的努力留下足迹 喜欢的话可以点个赞谢谢了。 数组 数组是一推相同数据…...
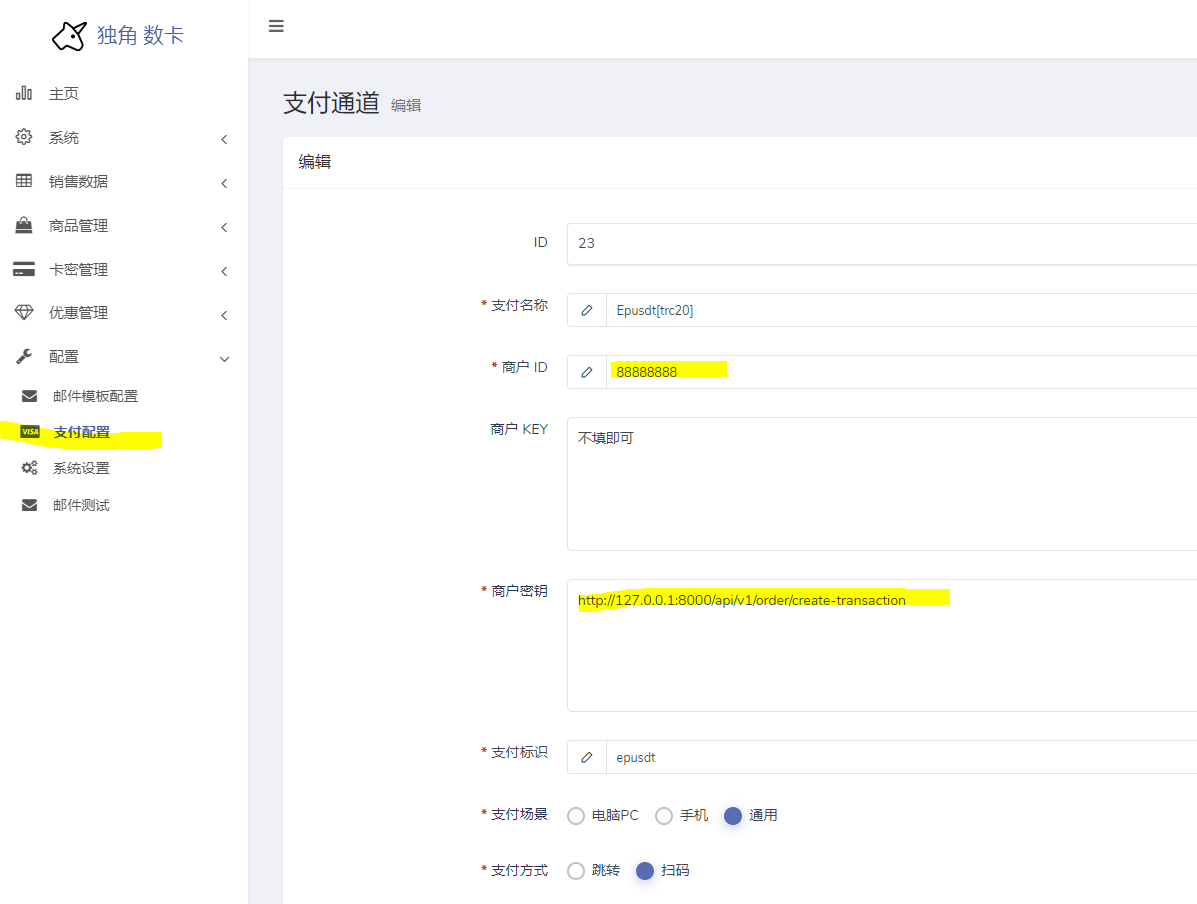
2024年5月份最新独角数卡使用USDT详细小白教程
直观配套视频教程 2024年5月份最新独角数卡安装及USDT使用详细小白教程 1、创建服务器 Centos或者Ubuntu2、宝塔面板开心版安装寶塔 Linux 面版 8.0.5 開心版 - 2024年1月12日 - 开心专区 - 异次元 - Powered by Discuz!Centos安装命令(默认安装是 8.0.1 直接在线升…...

【idea】idea2024最新版本下载_安装_破解
1、下载 下载地址:下载 IntelliJ IDEA – 领先的 Java 和 Kotlin IDE 下载完成: idea破解脚本下载链接:https://pan.baidu.com/s/1L5qq26cRABw8XuEn_CngKQ 提取码:6666 下载完成: 2、安装 1、双击idea的安装包&…...
部署CNI网络组件+k8s多master集群部署+负载均衡
一、环境部署 主机服务 192.168.91.5 K8S集群master01192.168.91.8 K8S集群master02192.168.91.6K8S集群node01192.168.91.7K8S集群node02192.168.91.9 负载均衡nginxkeepalive01(master)192.168.91.10 负载均衡nginxkeepalive02(backup&am…...
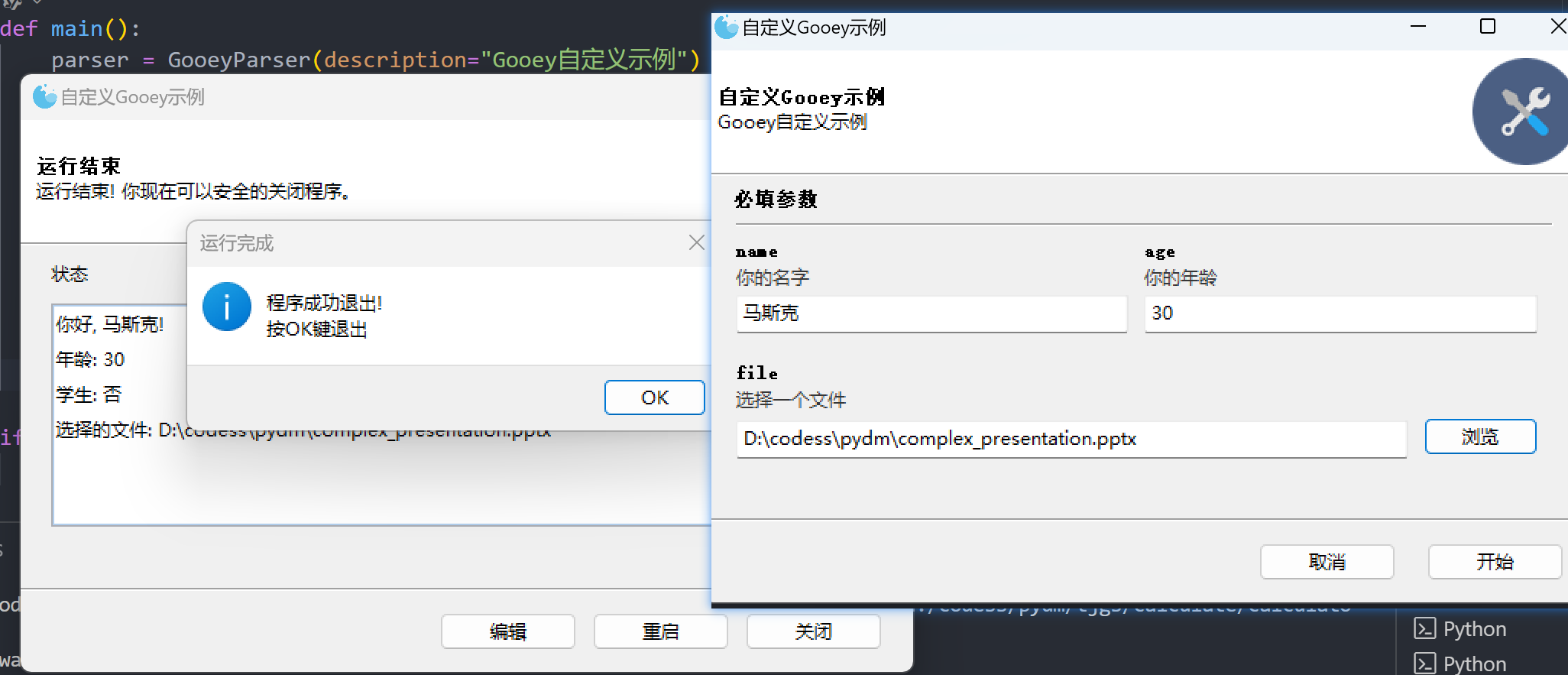
一个和蔼可亲的Python库,用Gooey为你的程序添加GUI
大家好,你有没有遇到过这样的情况:你写了一个非常棒的命令行程序,但当你分享给朋友或同事时,他们却因为害怕命令行而不愿意使用?这时候,一个简洁美观的图形用户界面(GUI)就派上用场了…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...
