使用 RT 矩阵进行 3D 点云变换详解(基于 PCL 和 Eigen 库)
在 3D 点云处理中,RT 矩阵是一个常用的工具,用于对点云进行旋转和平移操作。本文将详细介绍 RT 矩阵的概念,并通过一个示例程序演示如何基于 PCL 和 Eigen 库将一帧点云进行矩阵变换再输出。
本教程的示例代码和点云数据可在 GitHub 下载。
什么是 RT 矩阵
RT 矩阵包含旋转矩阵(R)和平移向量(T),组合起来可以描述一个刚体变换。具体来说,RT 矩阵是一个 4x4 的同质坐标变换矩阵,包含两个部分:
- 旋转矩阵(R):这是一个 3x3 的矩阵,用于描述点云的旋转。旋转矩阵是一个正交矩阵,表示绕某个轴的旋转。
- 平移向量(T):这是一个 3x1 的向量,用于描述点云的平移。平移向量表示在各个方向上的移动距离。
组合起来,RT 矩阵可以表示为:
|-------> This column is the translation| 1 0 0 x | \| 0 1 0 y | }-> The identity 3x3 matrix (no rotation) on the left| 0 0 1 z | /| 0 0 0 1 | -> We do not use this line (and it has to stay 0,0,0,1)
其中,R 是 3x3 的旋转矩阵,T 是 3x1 的平移向量,右下角的 1 是为了使矩阵成为同质坐标形式的 4x4 矩阵。
旋转矩阵(R)
旋转矩阵通常可以通过欧拉角、旋转向量或四元数来计算。
欧拉角:通过绕固定轴(如 X, Y, Z 轴)依次旋转相应的角度来构建旋转矩阵。例如:
-
绕 X 轴旋转角度( α \alpha α )
R x ( α ) = [ 1 0 0 0 cos α − sin α 0 sin α cos α ] \mathbf{R_x}(\alpha) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\alpha & -\sin\alpha \\ 0 & \sin\alpha & \cos\alpha \end{bmatrix} Rx(α)= 1000cosαsinα0−sinαcosα -
绕 Y 轴旋转角度( β \beta β )
R y ( β ) = [ cos β 0 sin β 0 1 0 − sin β 0 cos β ] \mathbf{R_y}(\beta) = \begin{bmatrix} \cos\beta & 0 & \sin\beta \\ 0 & 1 & 0 \\ -\sin\beta & 0 & \cos\beta \end{bmatrix} Ry(β)= cosβ0−sinβ010sinβ0cosβ -
绕 Z 轴旋转角度( γ \gamma γ )
R z ( γ ) = [ cos γ − sin γ 0 sin γ cos γ 0 0 0 1 ] \mathbf{R_z}(\gamma) = \begin{bmatrix} \cos\gamma & -\sin\gamma & 0 \\ \sin\gamma & \cos\gamma & 0 \\ 0 & 0 & 1 \end{bmatrix} Rz(γ)= cosγsinγ0−sinγcosγ0001
通过将这些旋转矩阵按顺序相乘,可以得到最终的旋转矩阵 R \mathbf{R} R。
旋转向量:通过旋转轴和旋转角度来构建旋转矩阵。旋转向量表示绕一个单位向量旋转一定角度,使用 Rodrigues 公式可以将其转换为旋转矩阵。
四元数:四元数是一种表示旋转的方式,能够避免欧拉角的万向节锁问题。通过四元数转换公式可以得到旋转矩阵。
平移向量(T)
平移向量是一个简单的 3x1 向量,表示在 X, Y, Z 三个方向上的平移量:
T = [ t x t y t z ] \mathbf{T} = \begin{bmatrix} t_x \\ t_y \\ t_z \end{bmatrix} T= txtytz
应用 RT 矩阵
假设有一个 3D 点 P = [ x y z ] T \mathbf{P} = \begin{bmatrix} x & y & z \end{bmatrix}^T P=[xyz]T,其同质坐标表示为 P h = [ x y z 1 ] T \mathbf{P_h} = \begin{bmatrix} x & y & z & 1 \end{bmatrix}^T Ph=[xyz1]T。
应用 RT 矩阵进行变换可以表示为: P h ′ = R T ⋅ P h \mathbf{P'_h} = \mathbf{RT} \cdot \mathbf{P_h} Ph′=RT⋅Ph 。
其中, P h ′ = [ x ′ y ′ z ′ 1 ] T \mathbf{P'_h} = \begin{bmatrix} x' & y' & z' & 1 \end{bmatrix}^T Ph′=[x′y′z′1]T ,展开后为:
[ x ′ y ′ z ′ 1 ] = [ R 11 R 12 R 13 t x R 21 R 22 R 23 t y R 31 R 32 R 33 t z 0 0 0 1 ] ⋅ [ x y z 1 ] \begin{bmatrix} x' \\ y' \\ z' \\ 1 \end{bmatrix} = \begin{bmatrix} R_{11} & R_{12} & R_{13} & t_x \\ R_{21} & R_{22} & R_{23} & t_y \\ R_{31} & R_{32} & R_{33} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} x′y′z′1 = R11R21R310R12R22R320R13R23R330txtytz1 ⋅ xyz1
经过计算,变换后的点 P ′ \mathbf{P'} P′ 的坐标为:
P ′ = [ x ′ y ′ z ′ ] = R ⋅ [ x y z ] + T \mathbf{P'} = \begin{bmatrix} x' \\ y' \\ z' \end{bmatrix} = \mathbf{R} \cdot \begin{bmatrix} x \\ y \\ z \end{bmatrix} + \mathbf{T} P′= x′y′z′ =R⋅ xyz +T
通过 RT 矩阵的应用,可以对一整帧点云的每一个点进行旋转和平移,从而实现点云的刚体变换。
示例程序
下面使用 PCL 库(Point Cloud Library)来实现将一帧点云经过 RT 矩阵转换输出另一帧点云,并将两帧点云同时可视化进行对比的演示。完整示例代码如下所示。
#include <pcl/point_types.h>
#include <pcl/io/pcd_io.h>
#include <pcl/visualization/pcl_visualizer.h>
#include <pcl/common/transforms.h>
#include <Eigen/Dense>
#include <thread>
#include <chrono>int main(int argc, char** argv)
{// 检查命令行参数if (argc != 2) {PCL_ERROR("Usage: %s <input.pcd>\n", argv[0]);return -1;}// 创建点云对象并读取PCD文件pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);if (pcl::io::loadPCDFile<pcl::PointXYZ>(argv[1], *cloud) == -1) {PCL_ERROR("Couldn't read the file %s\n", argv[1]);return -1;}// 创建RT矩阵,将矩阵初始化为单位矩阵Eigen::Matrix4f transform = Eigen::Matrix4f::Identity();// 定义旋转矩阵 (绕Z轴旋转45度)float theta = M_PI / 4; // 弧度制角度transform(0, 0) = cos(theta);transform(0, 1) = -sin(theta);transform(1, 0) = sin(theta);transform(1, 1) = cos(theta);// 定义平移向量 (平移 x 方向2.5米, y 方向0米, z 方向1米)transform(0, 3) = 2.5;transform(1, 3) = 0.0;transform(2, 3) = 1.0;// 创建变换后的点云pcl::PointCloud<pcl::PointXYZ>::Ptr transformed_cloud(new pcl::PointCloud<pcl::PointXYZ>);pcl::transformPointCloud(*cloud, *transformed_cloud, transform);// 创建可视化对象pcl::visualization::PCLVisualizer::Ptr viewer(new pcl::visualization::PCLVisualizer("3D Viewer"));viewer->setBackgroundColor(0, 0, 0);// 设置原始点云的颜色为白色pcl::visualization::PointCloudColorHandlerCustom<pcl::PointXYZ> original_color(cloud, 255, 255, 255);viewer->addPointCloud<pcl::PointXYZ>(cloud, original_color, "original cloud");// 设置变换后点云的颜色为红色pcl::visualization::PointCloudColorHandlerCustom<pcl::PointXYZ> transformed_color(transformed_cloud, 255, 0, 0);viewer->addPointCloud<pcl::PointXYZ>(transformed_cloud, transformed_color, "transformed cloud");// 设置点云大小viewer->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 1, "original cloud");viewer->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 1, "transformed cloud");// 添加坐标系viewer->addCoordinateSystem(1.0);viewer->initCameraParameters();// 开始可视化while (!viewer->wasStopped()) {viewer->spinOnce(100);std::this_thread::sleep_for(std::chrono::milliseconds(100));}return 0;
}
改程序依赖 PCL 库和 VTK 库,配套 CMakeLists.txt 文件如下:
cmake_minimum_required(VERSION 3.1)
project(transform_demo)find_package(PCL REQUIRED)
find_package(VTK REQUIRED)include_directories(${PCL_INCLUDE_DIRS})
link_directories(${PCL_LIBRARY_DIRS})
add_definitions(${PCL_DEFINITIONS})add_executable(${PROJECT_NAME} transform_demo.cpp)
target_link_libraries(${PROJECT_NAME} ${PCL_LIBRARIES} ${VTK_LIBRARIES})
依次执行以下命令编译源代码:
$ mkdir build && cd build
$ cmake ..
$ make
编译完成后,执行 transform_demo 演示程序,指定 PCD 文件:
$ ./transform_demo ../data/2024-04-09-22-06-07.pcd
输出结果如下:

可以看到,白色为原始点云,红色为经过旋转、平移后的点云。
小结
矩阵变换是点云处理中的一个重要的工具,本文介绍了 RT 矩阵的基本概念和计算方法,RT 矩阵可用于对 3D 点云进行旋转和平移操作。我们通过一个例子演示了如何通过 PCL 和 Eigen 构建 RT 矩阵并实现 3D 点云的旋转平移,相信你已经掌握点云的矩阵变换操作。

相关文章:

使用 RT 矩阵进行 3D 点云变换详解(基于 PCL 和 Eigen 库)
在 3D 点云处理中,RT 矩阵是一个常用的工具,用于对点云进行旋转和平移操作。本文将详细介绍 RT 矩阵的概念,并通过一个示例程序演示如何基于 PCL 和 Eigen 库将一帧点云进行矩阵变换再输出。 本教程的示例代码和点云数据可在 GitHub 下载。 什…...

CTFHUB技能树——SSRF(二)
目录 上传文件 FastCGI协议 Redis协议 上传文件 题目描述:这次需要上传一个文件到flag.php了.祝你好运 index.php与上题一样,使用POST请求的方法向flag.php传递参数 //flag.php页面源码 <?phperror_reporting(0);if($_SERVER["REMOTE_ADDR&…...

Vue3实现简单的瀑布流效果,可抽离成组件直接使用
先来看下效果图: 瀑布流中的内容可进行自定义,这里的示例图是通过不同背景颜色的展示进行区分,每个瀑布流中添加了自定义图片和文字描述。 实现方式: 1.建立子组件(可单独抽离)写出瀑布流的样式 文件名为…...

【已解决】C#如何消除Halcon上一次显示窗口的涂层
前言 在通过C#进行封装Halcon的时候发现一个问题,就是如果我重新去标定一个图像的时候不能把上一次的清掉,然后之前的会覆盖掉原来的,这个确实是这样,但是如果说现在的图像面积比之前的小的那么就没有任何效果显示,因…...
XShell-连接-Centos 7
XShell 连接Centos 7 一.准备 安装XShell XShell下载地址: 在虚拟机上安装Centos 7,具体操作自行学习 二.Centos 7的准备 1.网络适配器修改为NAT 2.获取IP 输入命令: ip addr我的Centos 7对外IP为192.168.174.129 三.XShell连接Cento…...

vue3 组件刷新
在 Vue 3 中,如果你想刷新一个组件,有几种方法可以实现。 使用 key 属性: 当你想要强制重新渲染一个组件时,你可以为其添加一个独特的 key 属性。当 key 属性的值改变时,Vue 会强制组件重新创建。 <template> <MyComp…...
Java进阶学习笔记14——模板方法设计模式
面试和看源码。 谈到设计模式: 1、解决了什么问题? 2、怎么写? 模板方法设计模式解决了什么问题? 解决方法中存在重复代码的问题。 写法: 1)定义一个抽象类: 2)在里面定义两个方…...
Centos7静态路由和动态路由
路由,即路由选择(Routing),是指在计算机网络中选择数据传输路径的过程。路由器(Router)是执行路由选择功能的网络设备。路由的主要目的是在复杂的网络结构中,选择最佳路径将数据包从源节点传递到…...

戴尔(Dell)服务器运行状况监控
戴尔(Dell)服务器因其加速的性能、增强的自动化和简化的管理而受到全球许多组织的青睐,许多组织将其业务关键应用程序和功能放在戴尔(Dell)服务器中,因此,有效的戴尔(Dell࿰…...
微信小程序毕业设计-智慧旅游平台系统项目开发实战(附源码+演示视频+LW)
大家好!我是程序猿老A,感谢您阅读本文,欢迎一键三连哦。 💞当前专栏:微信小程序毕业设计 精彩专栏推荐👇🏻👇🏻👇🏻 🎀 Python毕业设计…...
抖音小店新规又来了!平台下调了两项门槛,惊掉商家下巴!
大家好,我是电商糖果 平台这几年为了快速发展电商项目,一直在向商家释放友好政策,目的就是为了吸引更多的商家入驻。 这不官方5月30日起下调了两个门槛,让不少商家大呼不可思议。 第一个就是保证金下调。 平台按照商家经营类目…...

【启程Golang之旅】运算符与流程控制讲解
欢迎来到Golang的世界!在当今快节奏的软件开发领域,选择一种高效、简洁的编程语言至关重要。而在这方面,Golang(又称Go)无疑是一个备受瞩目的选择。在本文中,带领您探索Golang的世界,一步步地了…...

Docker: exec命令浅析
简介 Docker exec命令是Docker提供的一个强大工具,用于在正在运行的容器中执行命令。在此将介绍Docker exec命令的用法和示例,帮助大家更好地理解和使用这个命令。 Docker是一种流行的容器化平台,允许用户在容器中运行应用程序。有时候&#…...

c++的查漏补缺 1、函数指针
今天写链表的插入排序时遇到了一个问题 void InsertionSortList(ListNode* head, int n){if (!head||!head->next) return nullptr;auto dummy new ListNode(-1);dummy->next head;auto pre head;auto cur head->next;while (cur ! NULL){auto tmp dummy;if (pre…...
uniapp+php服务端实现苹果iap内购的消耗性项目和非续期订阅项目,前后端代码加逻辑分析
前言:公司的项目app在上架苹果商店时发现人家要求里面的部分购买项目必须使用iap购买的方式,使用原本的微信支付方式审核不给通过,无奈只能重新研究这个东西。做起来还是有点麻烦,主要是网上的文章很少,不能直接硬抄。…...

【代码随想录】【算法训练营】【第11天】 [20]有效的括号 [1047]删除字符串中的所有相邻重复项 [150]逆波兰表达式求值
前言 思路及算法思维,指路 代码随想录。 题目来自 LeetCode。 day 11,周六,又开始变的困难了~ 题目详情 [20] 有效的括号 题目描述 20 有效的括号 解题思路 前提:括号匹配 思路:利用栈的后入先出特性…...

vue实现图片懒加载
在src中创建一个directives文件夹在里面创建一个lazy.js文件 在main.js中引入 import lazy from ./directives/lazy app.directive(lazy, lazy) 在app.vue中 <script setup lang"ts"> import { RouterLink, RouterView } from vue-router import HelloWorl…...
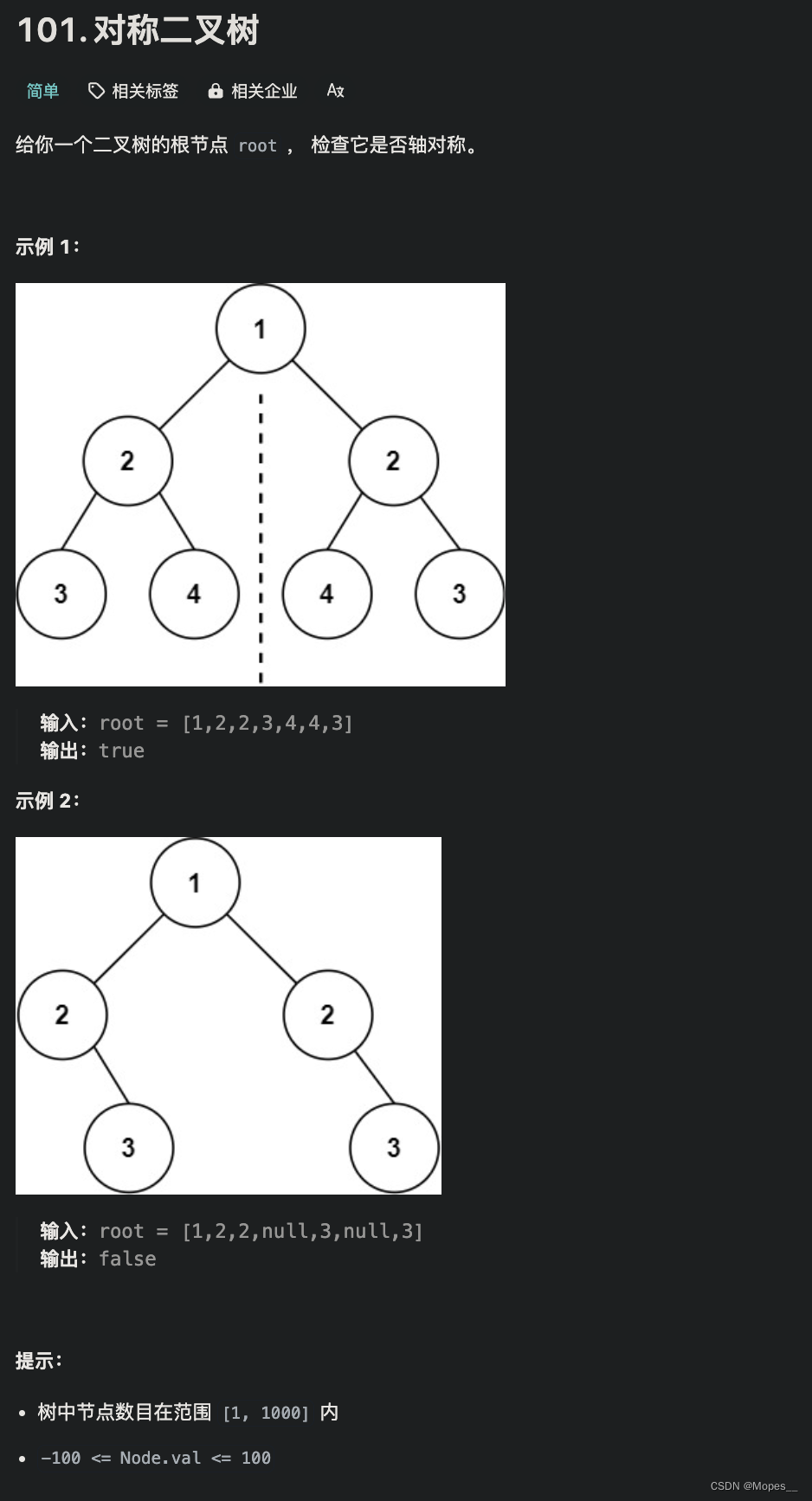
Python | Leetcode Python题解之第101题对称二叉树
题目: 题解: class Solution:# 在【100. 相同的树】的基础上稍加改动def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:if p is None or q is None:return p is qreturn p.val q.val and self.isSameTree(p.left, q.ri…...

周报5.20~5.26
学习内容: 主要了解了Qt的信号和槽、ui页面布局、各类常见控件的使用、绘图事件以及文件操作的相关知识,并且完成相关案例的设计。练习代码了解了多层感知机、激活函数、多项式回归、高维线性回归、暂退法、分布偏移、深度学习计算等相关知识与代码案例…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...

SQL进阶之旅 Day 22:批处理与游标优化
【SQL进阶之旅 Day 22】批处理与游标优化 文章简述(300字左右) 在数据库开发中,面对大量数据的处理任务时,单条SQL语句往往无法满足性能需求。本篇文章聚焦“批处理与游标优化”,深入探讨如何通过批量操作和游标技术提…...