数位dp-- 数字游戏
题目
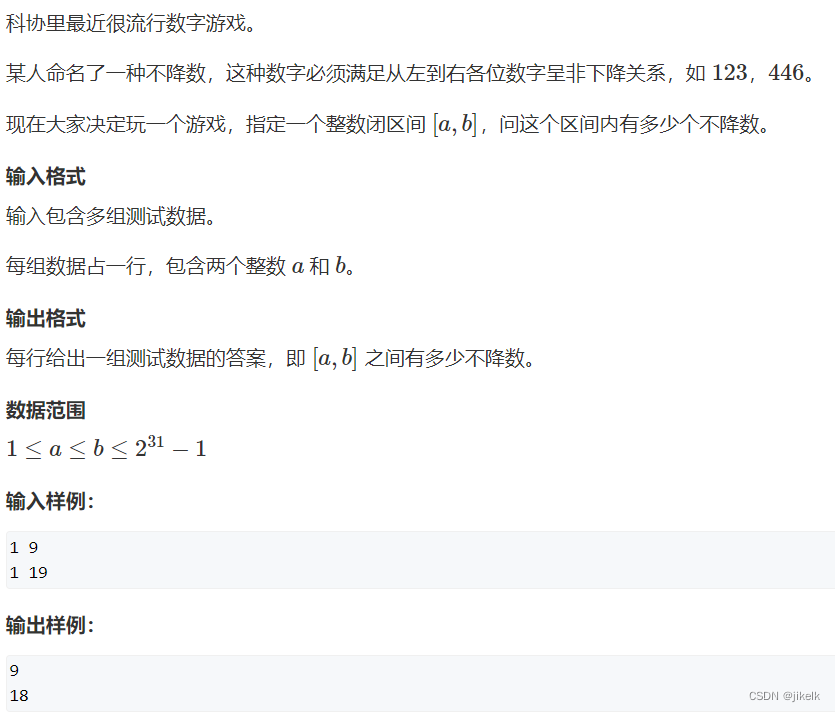
思路
也是一道比较典型的数位dp的问题,关键的思想跟我上一篇博客很像,
首先把区间值变成[1,Y]-[1,X-1]的值,然后单独计算得到结果。
总的来说就是把这个数的每一位都单独拿出来,然后根据选0-an-1和选**an**两种方案单独计算:
当选第一种方案时,就是后面的i位**(因为最低为从a0开始)的数字可以任意选,那么就可以表示为前面的最高位为last**,一共i+1位的决策数。
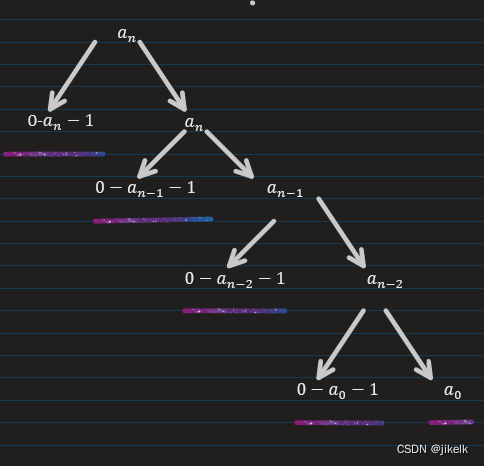
ps:上一篇博客的图(
那么这里求决策数就需要用到动态规划了。
这里用f[i][j]表示前面的最高位为j,并且一共有i位的不降数的集合,
那么f[i][j]肯定要从前面的状态中得到,那么在第i位为j的时候,
i-1位的选择可以为 j , j + 1 , j + 2 ,… , 9这些情况,
这些情况之和就相当于f[ i ] [ j ] , 那么f [ i ] [ j ]就可以表示为f[ i -1] [ j ]+f [ i-1 ] [ j + 1 ]+…+f [ i -1] [ 9 ]。这里可以预处理获得所有情况的f[ i ] [ j ],这样上面的方案数就可以直接算出来了(这里借用了y总的图片一用)
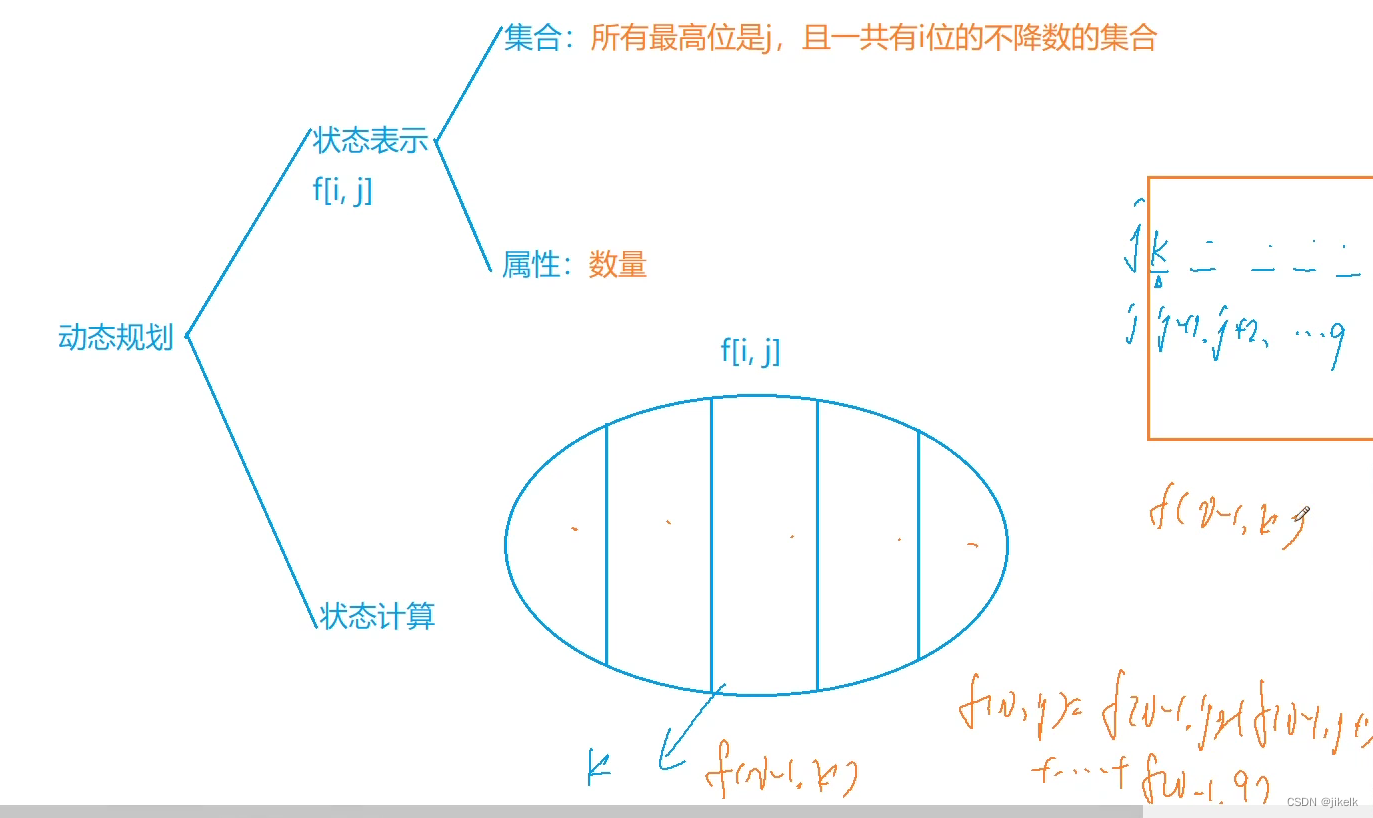
当选第二种方案时
即要选择当前位的最大值时,要进行特判,即上一位的最大值是不是小于当前位的最大值的,(即last<x)如果不满足则不能走到下一位直接返回,如果满足则直接进行最大值的覆盖。然后走到最右下角的决策时如果还是能选到a0,那么就作为一种方案数使res++,然后返回res即可。
具体代码
#include<cstdio>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include<vector>
#include<queue>
#include<map>
#define sc_int(x) scanf("%d", &x)
#define sc_ll(x) scanf("%lld", &x)
#define pr_ll(x) printf("%lld", x)
#define pr_ll_n(x) printf("%lld\n", x)
#define pr_int_n(x) printf("%d\n", x)
#define ll long long
using namespace std;const int N=20;
int n ,m,h;
int s[N][N];void cal()
{for(int i =0;i<=9;i++)s[1][j]=1;for(int i =1;i<=N;i++)for(int j =0;j<=9;j++)for(int k=j;k<=9;k++)s[i][j]+=s[i-1][k];
}int dp(int n)
{if(!n) return 1;//特判,如果为0也可以作为一种决策vector<int>cnt;while(n)cnt.push_back(n%10),n/=10;int res=0;int last=0;for(int i =cnt.size()-1;i>=0;i--){int x=cnt[i];for(int j =last;j<x;j++)res+=s[i+1][j];if(last>x)break;x=last;if(!i)res++;}return res;
} int main()
{int t;cal();int l,r;while(cin>>l>>r)cout<<dp(r)-dp(l-1)<<endl;return 0;
}
ps:作为数位dp的第二篇,感觉理解起来容易了很多(最不好理解的点还是方案数的预处理哪里),希望以后的数位dp能越学越熟悉吧。
相关文章:

数位dp-- 数字游戏
题目 思路 也是一道比较典型的数位dp的问题,关键的思想跟我上一篇博客很像, 首先把区间值变成[1,Y]-[1,X-1]的值,然后单独计算得到结果。 总的来说就是把这个数的每一位都单独拿出来,然后根据选0-an-1和选**an**两种方案单独计算&…...

Linux脚本 启动、重启、停止、授权
在jar包所在目录 vim start.sh | reload.sh | stop.sh输入以下命令 然后保存,进行授权 1.启动 nohup java -jar -Dfile.encodingutf-8 IntegrationFrame-sso-1.0.0-SNAPSHOT.jar & echo "started"2.重启 pid$(ps -ef|grep IntegrationFrame-sso-1.…...
Pytorch深度学习实战3-8:详解数据可视化组件TensorBoard安装与使用
目录1 什么是Tensorboard?2 Tensorboard安装3 Tensorboard可视化流程4 Tensorboard可视化实例4.1 常量可视化4.2 特征图可视化1 什么是Tensorboard? 在深度学习领域,网络内部如同黑箱,其中包含大量的连接参数,这给人工…...
【独家】)
华为OD机试 - 旋转骰子(C 语言解题)【独家】
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧文章目录 使用说明本期题目:旋转骰子…...

如何做SpringBoot单元测试?
前言单元测试(unit testing),是指对项目中的最⼩可测试单元进⾏检查和验证的过程就叫单元测试,对于Java来说或者是在SpringBoot项目中,最小的可测试单元就是一个方法。做单元测试就是为了证明某段代码的执⾏结果是否符…...

ZZULI训练: 数组和字符串专题
ZZULI训练:数组和字符串专题ZZULI训练: 数组和字符串专题ZZULI训练:数组和字符串专题 部分多实例没写循环多次是因为在main里面循环了, 你们写的时候要加上只提供大概思路和核心代码建议多尝试一下c, 并没有想象的那么难 7-1 个位数统计 可以开个数组来存一下每个数组出现的…...

ElasticSearch如何解决深分页问题?
文章目录 前言From/Size参数Query阶段Fetch阶段深度分页问题Scroll遍历数据基本使用遍历优缺点缺点:优点:」Scroll Scan基本使用Scroll Scan与Scroll的区别Sliced ScrollSearch After基本使用基本原理优缺点总结ES7版本变...
JDK8新特性宝典
JDK8新特性 Java 是第一大编程语言和开发平台。它有助于企业降低成本、缩短开发周期、推动创新以及改善应用服务。如今全球有数百万开发人员运行着超过 51 亿个 Java 虚拟机,Java 仍是企业和开发人员的首选开发平台 课程内容的介绍 了解Java发展史Lambda表达式…...

【C++】关于C++模板的分离编译问题
文章目录1.阐述模板的实例化和重复定义问题2.分离编译可能出现的问题3.解决方法将函数模板的定义放到头文件中模板定义的位置显式实例化模板总结1.阐述模板的实例化和重复定义问题 C模板是一种非常强大的工具,可以为我们提供通用的代码实现方式。然鹅,在…...
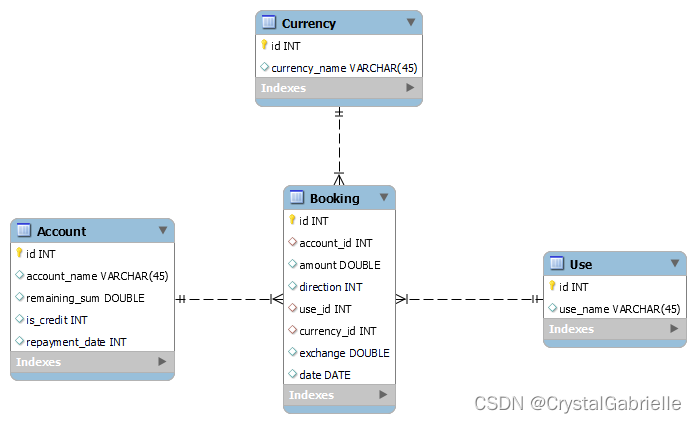
小应用记账本-第2章-数据库设计
小应用记账本-第2章-数据库设计 在上一章《小应用记账本-第1章-需求分析》已经罗列了我们需要的功能,因为很简单,所以这一章就来设计数据库吧。 Account表:账户表 字段名类型说明取值idint账户idaccount_namevarchar账户名称remaining_sumd…...

Spring Boot+Vue前后端分离项目练习06之网盘项目创建vue项目
1.安装环境 构建vue项目,需要提前安装相应的环境,这里主要就是node,npm和Vue CLl。 #1、安装nodejs brew install nodejs #2、再执行下面命令来安装npm(npm是开发nodejs时所用的依赖库) brew install npm #3、安装vue cli npm install -g v…...

Python - 单元测试
python-单元测试1 Unittest2 Pytest3 两者区别断言方面用例执行编写规则前后置操作setUp, setUpclass, setUpmodule 区别4 实战操作unittest:pytest:1 Unittest unittest属于python的内置框架,支持多种自动化测试用例的编写,以及支持用例前置条件和后置…...
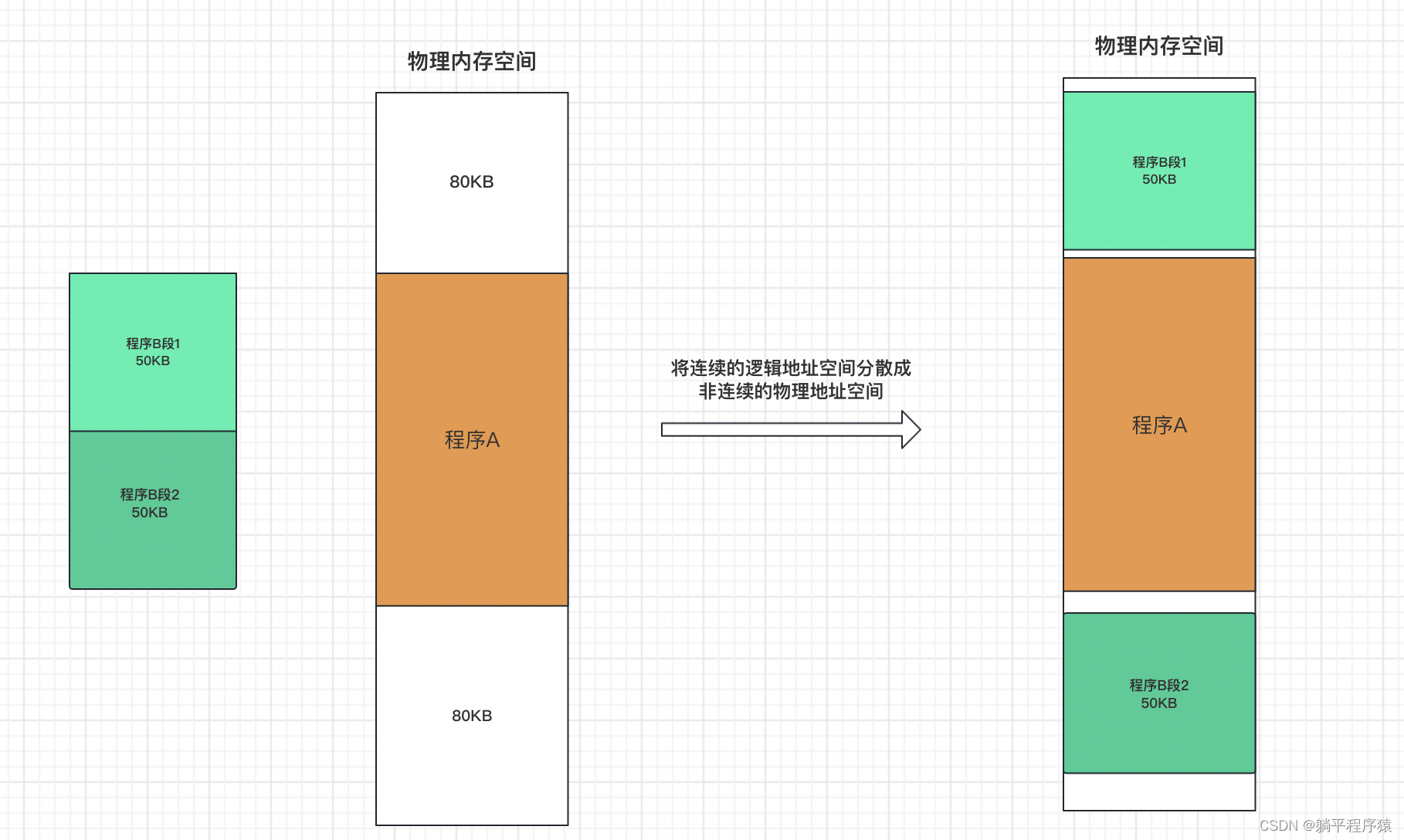
特权级那些事儿-实模式下分段机制首次出现的原因
前言: 操作系统的特权级模块在整个操作系统的学习中应该算的上是最难啃的了,提到特权级就要绕不开保护模式下的分段机制;如果想要彻底弄明白就要对比实模式下的分段机制有什么缺陷。这就衍生出很多问题如:什么是实模式?…...
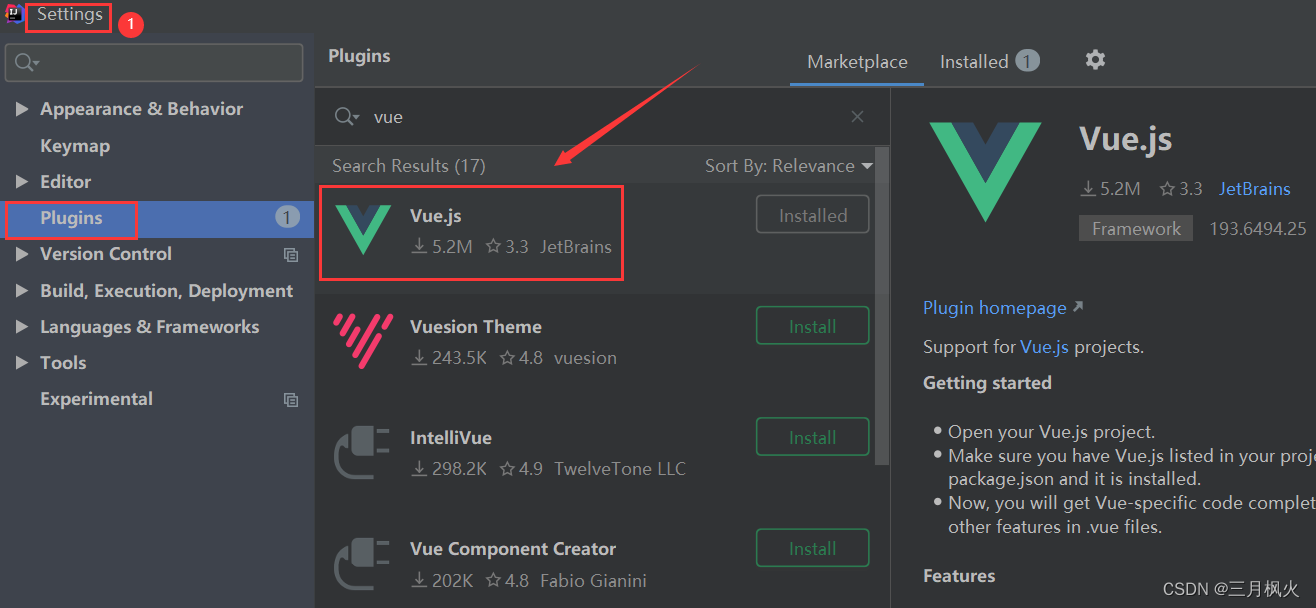
详解Vue安装与配置(2023)
文章目录一、官网下载node.js二、安装Node.js三、环境配置四、idea导入vue项目五、IDEA添加Vue.js插件一、官网下载node.js Vue是前端开发框架。搭建框架,首先要搭建环境。搭建Vue的环境工具:node.js(JavaScript的运行环境)&…...
TypeScript深度剖析:Vue项目中应用TypeScript?
一、前言 与link类似 在VUE项目中应用typescript,我们需要引入一个库vue-property-decorator, 其是基于vue-class-component库而来,这个库vue官方推出的一个支持使用class方式来开发vue单文件组件的库 主要的功能如下: metho…...

linux面试高级篇
题目目录1.虚拟机常用有几种网络模式?请简述其工作原理或你个人的理解?2. Dockerfile中最常见的指令是什么?3.docker网络模式有哪些?4.Kubernetes有哪些核心组件这些组件负责什么工作?5. Pod是什么?6.描述一…...

java 4 (面向对象上)
java——面向对象(上) 目录java——面向对象(上)面向对象的思想概述类的成员(1-2):属性和方法对象的内存解析类中属性的使用类中方法的使用1.举例:2.声明方法:3.说明4.re…...

HTTP报头的2个方法
在采集网页信息的时候,经常需要伪造报头来实现采集脚本的有效执行 下面,我们将使用urllib2的header部分伪造报头来实现采集信息 方法1、 #!/usr/bin/python -- coding: utf-8 -- #encodingutf-8 #Filename:urllib2-header.py import urllib2 import…...
yolov5双目检测车辆识别(2023年+单目+双目+python源码+毕业设计)
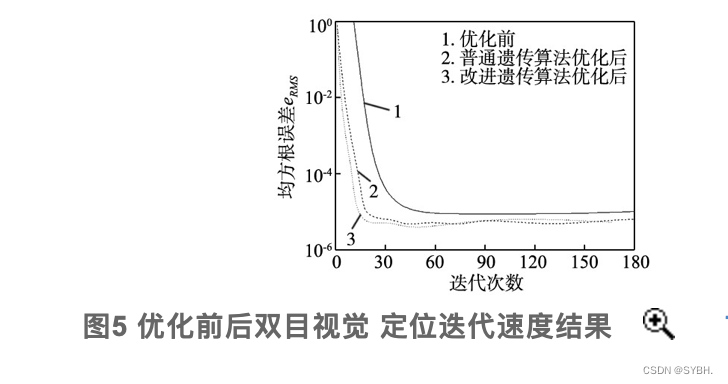
行人识别yolov5和v7对比yolo车距源码:yolov5双目检测车辆识别(2023年单目双目python源码毕业设计)上盒岛APP,开线上盲盒商店http://www.hedaoapp.com/yunPC/goodsDetails?pid4132 为了提高传统遗传算法(genetic algorithm, GA)IGA优化BP网络迭代时间过长以及精度偏…...

华为OD机试题,用 Java 解【用户调度问题】问题
华为Od必看系列 华为OD机试 全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典使用说明 参加华为od机试,一定要注意不…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...
