数理逻辑:1、预备知识
17.1 命题和联结词
命题:可以判定真假的陈述句。(则悖论,祈使句,疑问句都不是命题)
原子命题:不能被分割为更小的命题的命题
例如:
-
2既是素数又是偶数
可以由$p: 2 是素数, 2是素数, 2是素数,q: 2 是偶数,由 2是偶数,由 2是偶数,由p\land q$联结得来
-
只有在天晴时,我们才去郊游
可以有 p : p: p:天晴, q : q: q:去郊游,由 q → p q\rightarrow p q→p联结得来(q蕴含p,郊游时一定天晴,但天晴时不一定去郊游)
常用的联结词
- 非: ¬ \neg ¬,表示否定
- 合取: ∧ \land ∧,表示并且
- 析取: ∨ \lor ∨,表示或
- 蕴含: → \rightarrow →,表示“如果…,则…”的意思
- 等价: ↔ \leftrightarrow ↔,表示当且仅当
命题
形式化的递归定义,
命题是一个符号串,满足:
- 字母集中每个元素都是命题
- 如果 P , Q P,Q P,Q是命题,那么 ¬ P , P ∧ Q , P ∨ Q , P → Q , P ↔ Q \neg P,P\land Q,P\lor Q,P\rightarrow Q,P\leftrightarrow Q ¬P,P∧Q,P∨Q,P→Q,P↔Q也是命题
- 有限次使用1和2
但我们注意到,如此定义,会出现形如 P ¬ , ∧ Q P\neg ,\land Q P¬,∧Q的命题,这在日常生活中是不存在的,但从代数的角度是可以的,为此需要引入泛代数的概念
17.2 泛代数
困难的一节。
元:在群论中,我们指出,集合 A A A上的 n n n元运算实际上就是一个 n n n元单值函数 t : A n → A t: A^n\rightarrow A t:An→A,其中 n n n在之后就称为 t t t的元。
在群G中,定义一个一元运算 i : G → G i:G\rightarrow G i:G→G求逆元,即 i ( a ) = a − 1 i(a)=a^{-1} i(a)=a−1
对于0元运算,实际上是从集合 A 0 A^0 A0(只有一个元素,通常记为 ∅ \varnothing ∅到A上的函数),即 t 0 : ∅ → A t_0:\varnothing\rightarrow A t0:∅→A,因此0元运算实质上是唯一对应了 A A A上的某个元素,故0元运算通常可视为 A A A中的一个特殊元素。
在群论中,定义0元运算 e ∗ : ∅ → G , e ∗ ( ∅ ) = e e^*:\varnothing \rightarrow G,e^*(\varnothing) =e e∗:∅→G,e∗(∅)=e,其中 e e e为单位元,实际上 e ∗ e^* e∗给出了群G的单位元,之后我们将 e ∗ e^* e∗看作单位元 e e e,也可以把 e e e看作0元运算。
定义1 类型
设 a r ar ar为集合 T T T到非负整数集 N N N的函数,则称集合 T T T和函数 a r ar ar为一个类型,记为 T = ( T , a r ) T=(T,ar) T=(T,ar),简记为 T T T。此外,令 T n = { t ∈ T ∣ a r ( t ) = n } T_n=\{t\in T| ar(t) =n\} Tn={t∈T∣ar(t)=n}
定义2 T-代数
A是一个集合,T是一个类型,T中每个元素 t t t对应于 A A A上的一个函数: t A : A a r ( t ) → A t_A:A^{ar(t)}\rightarrow A tA:Aar(t)→A,则称集合 A A A和 { t A ∣ t ∈ T } \{t_A|t\in T\} {tA∣t∈T}构成类型 T T T的一个代数 A A A,称为T-代数,元素 t ∈ T n t\in T_n t∈Tn称为 n n n元T-代数运算
定义3 T-代数相等
T-代数A,B相等 ⟺ ∀ t ∈ T , t A = t B \Longleftrightarrow \forall t\in T,t_A=t_B ⟺∀t∈T,tA=tB,记为 T A = T B T_A=T_B TA=TB
定义4 T-子代数
设A是一个T-代数,B为A的子集,如果将A上的运算限制在B上仍然构成一个T-代数,即:对任意的非负整数n,任意的 t ∈ T n . b 1 , b 2 , ⋯ , b n ∈ B t\in T_n.b_1,b_2,\cdots,b_n\in B t∈Tn.b1,b2,⋯,bn∈B,有 t A ( b 1 , ⋯ , b n ) ∈ B t_A(b_1,\cdots,b_n)\in B tA(b1,⋯,bn)∈B成立(封闭的),则称B是A的一个T-子代数
定义5 T-代数同态
设A,B是T-代数, φ \varphi φ是从A到B的映射,若对任意 t ∈ T , a 1 , ⋯ , a n ∈ A ( n = a r ( t ) ) t\in T,a_1,\cdots,a_n\in A(n=ar(t)) t∈T,a1,⋯,an∈A(n=ar(t)),有 φ ( t A ( a 1 , ⋯ , a n ) ) = t B ( φ ( a 1 ) , ⋯ , φ ( a n ) ) \varphi(t_A(a_1,\cdots,a_n))=t_B(\varphi(a_1),\cdots,\varphi(a_n)) φ(tA(a1,⋯,an))=tB(φ(a1),⋯,φ(an)),则称 φ \varphi φ为从 A A A到 B B B的同态映射,当 φ \varphi φ是满射时,称A和B市同态的。
特别地,当 φ \varphi φ是同态映射,且可逆时,称 φ \varphi φ为同构映射,称 A , B A,B A,B是同构的,此时逆函数 φ − 1 \varphi ^{-1} φ−1是从B到A的同构映射。
定义6 自由T代数
设X是集合,G是一个T-代数, σ \sigma σ为X到G的函数,若对每个T-代数A和X到A的函数 τ \tau τ,都存在唯一的G到A的同态映射 φ \varphi φ,使得 φ σ = τ \varphi \sigma = \tau φσ=τ,则称 G G G(更严格地说是 ( G , σ ) (G,\sigma) (G,σ))是生成集X上的自由T-代数。X中的元素为生成元。

引理1 自由T-代数中的内射
若 ( G , σ ) (G,\sigma) (G,σ)是X上的自由T-代数,则 σ \sigma σ是内射
定理1 自由T-代数存在性
对任何集合X和类型T,存在X上的自由T-代数,并且这种T-代数在同构意义下是唯一的。
证明是复杂的, P227
其中,出现了T-代数的构造方式:
T-代数的构造方式
- G 0 = T 0 ∪ X G_0 =T_0\cup X G0=T0∪X,假定 T 0 ∩ X = ∅ T_0\cap X =\varnothing T0∩X=∅
- 假定 G r G_r Gr已经确定,则
G n = { ( t , a 1 , ⋯ , a k ) ∣ t ∈ T k , k > 0 , a i ∈ G r i , ∑ k r i = n − 1 } G_n=\{(t,a_1,\cdots,a_k)|t\in T_k,k>0,a_i\in G_{r_i},\sum ^k r_i =n-1\} Gn={(t,a1,⋯,ak)∣t∈Tk,k>0,ai∈Gri,∑kri=n−1}
其中 G 0 G_0 G0可理解为原子命题, G n G_n Gn可理解为做了一些逻辑运算的若干个命题。
例如:
p , q ∈ G 0 , ¬ p ∈ G 1 , p ∧ q ∈ G 2 p,q\in G_0,\neg p \in G_1,p\land q \in G_2 p,q∈G0,¬p∈G1,p∧q∈G2
一个例子

注意,第一个元素为运算,例子中的 → \rightarrow →为二元运算,所以后面要选择两个元素,而由于 F F F是零元的,所以在 n > 0 n>0 n>0时,不能取F
由这种构造方式,我们可以自然地得到一个推论
推论1
设G是可列集 X = { x 1 , x 2 , ⋯ } X=\{x_1,x_2,\cdots\} X={x1,x2,⋯}上地自由T-代数,则G中每个元素都是某个有限子集 X n = { x 1 , ⋯ , x n } X_n=\{x_1,\cdots,x_n\} Xn={x1,⋯,xn}所生成地自由T-代数中的元素。
定义 7 T-代数变量
一个T-代数变量是一个自由T-代数的自由生成集的元素。
相关文章:

数理逻辑:1、预备知识
17.1 命题和联结词 命题:可以判定真假的陈述句。(则悖论,祈使句,疑问句都不是命题) 原子命题:不能被分割为更小的命题的命题 例如: 2既是素数又是偶数 可以由$p: 2 是素数,…...

14-云原生监控体系-Redis_exporter 监控 MySQL[部署Dashborad告警规则实战]
文章目录 环境准备切片集群主从哨兵1. 部署1.1. 二进制方式1.1.1. 下载二进制包1.1.2. 部署1.2. docker-compose 容器方式1.3. 配置连接&认证参数1.3.1. 连接认证参数1.3.2. 配置服务控制 systemd2. 配置到 Prometheus3 Dashboard4. 告警规则...

DOS学习-目录与文件应用操作经典案例-xcopy
新书上架~👇全国包邮奥~ python实用小工具开发教程http://pythontoolsteach.com/3 欢迎关注我👆,收藏下次不迷路┗|`O′|┛ 嗷~~ 目录 一.前言 二.使用 三.案例 一.前言 xcopy命令是DOS系统中一个强大的文件和目录复制工具&…...

Midjourney是一个基于GPT-3.5系列接口开发的免费AI机器人
Midjourney是一个基于GPT-3.5系列接口开发的免费AI机器人,旨在提供多领域的智能对话服务。Midjourney在不同领域中有不同的定义和应用,以下是对其中两个主要领域的介绍: Midjourney官网:https://www.midjourney.com/ 一、AI绘画工…...

v-model详解
目录 原理 作用 表单类组件封装 编辑v-model简化代码 原理 v-model本质上是一个语法糖。例如应用在输入框上,就是value属性和input属性的合写。 作用 提供数据的双向绑定。 数据变,视图跟着变:value视图变,数据跟着变input 注意&…...
ArcGIS中分割与按属性分割的区别
1、分割ArcGIS批量导出各个市的县级行政边界 视频教学: ArcGIS批量导出各个市的县级行政边界002 2、ArcGIS批量导出全国各省的边界 视频教学: ArcGIS导出全国各省的边界003 推荐学习: ArcGIS全系列实战视频教程——9个单一课程组合系列直播回…...
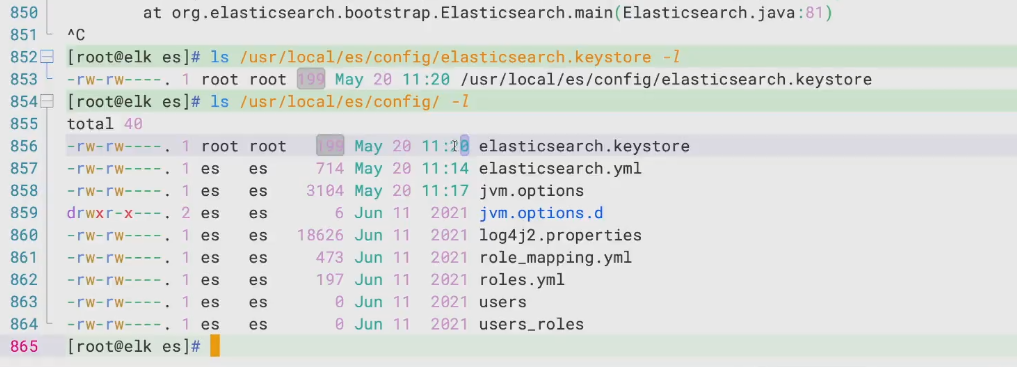
就业班 第三阶段(ELK) 2401--5.20 day1 ELK 企业实战 ES+head+kibana+logstash部署(最大集群)
ELKkafkafilebeat企业内部日志分析系统 1、组件介绍 1、Elasticsearch: 是一个基于Lucene的搜索服务器。提供搜集、分析、存储数据三大功能。它提供了一个分布式多用户能力的全文搜索引擎,基于RESTful web接口。Elasticsearch是用Java开发的ÿ…...

PCM和QAM
PCM(脉冲编码调制)和QAM(正交振幅调制)是两种不同的信号调制技术,它们在通信系统中有着不同的应用和特点。 PCM(脉冲编码调制) 概述 PCM是一种数字信号处理技术,用于将模拟信号转…...

Mongodb分布式id
1、分布式id使用场景 分布式ID是指在分布式系统中用于唯一标识每个元素的数字或字符串。在分布式系统中,各个节点或服务可能独立运行在不同的服务器、数据中心或地理位置,因此需要一种机制来确保每个生成的ID都是全局唯一的,以避免ID冲突。 …...

AI模型抉择:开源VS闭源,谁主沉浮?
AI模型抉择:开源VS闭源,谁主沉浮? 😄生命不息,写作不止 🔥 继续踏上学习之路,学之分享笔记 👊 总有一天我也能像各位大佬一样 🏆 博客首页 怒放吧德德 To记录领地 &am…...

佩戴安全头盔监测识别摄像机
佩戴安全头盔是重要的安全措施,尤其在工地、建筑工程和工业生产等领域,安全头盔的佩戴对于工人的生命安全至关重要。为了更好地管理和监控佩戴安全头盔的情况,监测识别摄像机成为了一项重要的工具。监测识别摄像机可以通过智能技术监测并记录…...

5.24学习记录
[FSCTF 2023]ez_php2 比较简单的pop链 <?php highlight_file(__file__); Class Rd{public $ending;public $cl;public $poc;public function __destruct(){echo "All matters have concluded";die($this->ending);}public function __call($name, $arg){for…...

创建FreeRTOS工程
创建STM32CubeMX工程 配置时钟 配置FreeRTOS 生成Keil MDK的工程 打开工程 结尾 这就是我们用STM32CubeMX创建的最基本的一个FreeRTOS的工程。可以看到,这个与我们使用stm32开发的裸机程序有相同的地方,也有不同的地方,我们可以发现&am…...

HTML中 video标签样式铺满全屏
video标签默认不是铺满的,即使手动设置宽高100%也不会生效,所以当需要video铺满div时,需要加上一个css样式 <videocontrolsstyle"width: 100%; height: 100%; object-fit: fill"autoplay:src"item.video" ></v…...

vue项目移动端商场
一、项目前端页面展示 二、项目整体目录结构 三、项目流程 1. vue快速创建基础项目 创建项目 vue create hk-shop 1 选择需要的配置 创建基础文件夹目录 src文件夹下文件夹目录: ① views 文件夹存放界面 ② components 文件夹存放界面中局部组件 ③ config 文件夹存…...

Golang | Leetcode Golang题解之第97题交错字符串
题目: 题解: func isInterleave(s1 string, s2 string, s3 string) bool {n, m, t : len(s1), len(s2), len(s3)if (n m) ! t {return false}f : make([]bool, m 1)f[0] truefor i : 0; i < n; i {for j : 0; j < m; j {p : i j - 1if i >…...
2024电工杯B题:大学生平衡膳食食谱的优化设计及评价
问题重述 大学时代是学知识长身体的重要阶段,同时也是良好饮食习惯形成的重要时期。这一特定年龄段的年轻人,不仅身体发育需要有充足的能量和各种营养素,而且繁重的脑力劳动和较大量的体育锻炼也需要消耗大量的能源物质。大学生中饮食结构不…...

齐护K210系列教程(三十二)_在线模型训练
在线模型训练 概念理解准备工作1 采集图像1.1 图像要求1.2 使用K210采集图片 2 标注图像3 打包数据集4 上传数据4.1创建项目4.1.1图像分类创建项目4.1.2图像检测创建项目 4.2上传数据4.2.1分类检测上传数据4.2.2图像检测上传数据 5 训练模型6 部署模型以及测试7 测试效果7.1图像…...
碌时刻必备!微信自动回复让你告别消息堆积
在忙碌的时候,我们往往会面临消息堆积如山的情况。无法及时回复消息不仅容易造成交流障碍,还可能错过重要的机会。 但是现在,有一个神奇的工具——个微管理系统,可以帮助我们轻松应对这个问题 ,实现微信自动回复。 首…...
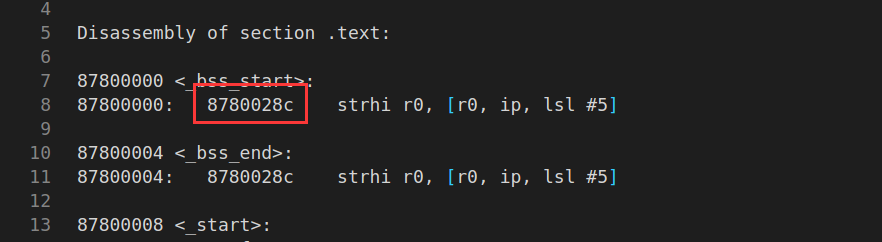
【ARM 裸机】按键输入
本节学习按键输入,先拷贝上一节工程文件, 1、驱动编写 新建 key 的 .h 和 .c 文件; 再查看一下硬件原理图如下; 由此可知,KEY0 按键接在 UART1_CTS 引脚上,默认情况下为高电平,按键按下为…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

前端调试HTTP状态码
1xx(信息类状态码) 这类状态码表示临时响应,需要客户端继续处理请求。 100 Continue 服务器已收到请求的初始部分,客户端应继续发送剩余部分。 2xx(成功类状态码) 表示请求已成功被服务器接收、理解并处…...

高保真组件库:开关
一:制作关状态 拖入一个矩形作为关闭的底色:44 x 22,填充灰色CCCCCC,圆角23,边框宽度0,文本为”关“,右对齐,边距2,2,6,2,文本颜色白色FFFFFF。 拖拽一个椭圆,尺寸18 x 18,边框为0。3. 全选转为动态面板状态1命名为”关“。 二:制作开状态 复制关状态并命名为”开…...

【汇编逆向系列】六、函数调用包含多个参数之多个整型-参数压栈顺序,rcx,rdx,r8,r9寄存器
从本章节开始,进入到函数有多个参数的情况,前面几个章节中介绍了整型和浮点型使用了不同的寄存器在进行函数传参,ECX是整型的第一个参数的寄存器,那么多个参数的情况下函数如何传参,下面展开介绍参数为整型时候的几种情…...
)
MySQL基本操作(续)
第3章:MySQL基本操作(续) 3.3 表操作 表是关系型数据库中存储数据的基本结构,由行和列组成。在MySQL中,表操作包括创建表、查看表结构、修改表和删除表等。本节将详细介绍这些操作。 3.3.1 创建表 在MySQL中&#…...
