误差反向传播简介与实现
误差反向传播
- 导语
- 计算图
- 反向传播
- 链式法则
- 反向传播结构
- 加法节点
- 乘法节点
- 实现简单层
- 加法
- 乘法
- 激活函数层实现
- ReLU
- Sigmoid
- Affine/Softmax层实现
- Affine
- 基础版
- 批版本
- Softmax-with-Loss
- 误差反向传播实现
- 梯度确认
- 总结
- 参考文献
导语
书上在前一章介绍了随机梯度下降法进行参数与权重的学习,但是实际上,SGD的训练过程很慢,并且,神经网络层与层之间是存在数学关系的,SGD并没有利用好他们间的这种关系,相比之下,利用数学式关系的误差反向传播,无论是在效率还是速度上都相较于随机梯度下降更胜一筹,也更为常用。
计算图
书上采用了计算图来描述传播过程,这里的图和数据结构中的图定义一样,简单实例如下:

如图,一般来说,计算图时一个有向无环图,使用计算图时需要先构建,然后再从左往右计算,像从左到右的计算方向,称之为正向传播(从出发点到结束点,有点类似网络流)。
计算图可以通过传递局部计算的结果来一层层的获得最终结果,如图中的x×y,这是一个局部结果,并不会干扰别的传递,计算图就是通过一步一步,一个个局部运算,最后得到结果的。
反向传播
如图,反向传播的计算顺序与正向传播相反,将信号E乘以局部导数,然后将结果传递下一个节点,局部导数为y关于x的导数,因为存在多参数的情况,所以这里是偏导,这种偏导是基于链式法则来实现的。

链式法则
链式法则是关于复合函数导数的性质,定义为:如果某个函数由复合函数表示,则该复合函数的导数可以由构成函数的各个函数的导数乘积表示。
具体的例子和证明属于高等数学内容,略,这里只说明链式法则和计算图的内容,一个简单的示例图如下。

根据链式法则∂z/∂t · ∂t/∂x=∂z/∂x,而原式 z = ( x − y ) 2 z=(x-y)^2 z=(x−y)2,则∂z/∂x= 2 ( x − y ) 2(x-y) 2(x−y)
反向传播结构
一般来说,计算图涉及到的运算都可以用加法和乘法表示,减法可以变成加负数,除法可以变成乘倒数,因此书上主要介绍了反向传播的加法节点和乘法节点的结构。
加法节点
以 z = x + y z=x+y z=x+y为例,计算图表示如下:

z对x,y的偏导都为1,反向传播图如下:

书上把上游传来的导数值设为∂L/∂z(最终输出值),由于链式法则,反向传播向下传递时要乘以z对x,y的偏导。
乘法节点
以 z = x y z=xy z=xy为例,计算图表示如下:

z对x,y的偏导分别为y、x,反向传播图如下:

可以看到,加法的反向传播只是将上游值传给下游,是不需要输入信号的,但是乘法的反向传播是需要正向传播的输入信号的。
实现简单层
承接上文,实现计算图中的乘法节点的,就是乘法层,实现加法节点就是加法层。
加法
给出书上的代码,方便理解加上了注释,按照个人习惯修改了一下:
class MulLayer:def __init__(self):#初始化self.x = Noneself.y = Nonedef forward(self, x, y):#赋值和返回正向传播结果self.x=xself.y=y return x*ydef backward(self, dout):#返回反向传播结果,注意需要输入导数return dout*self.y,dout*self.x乘法
同上:
class AddLayer:def __init__(self):#不需初始化passdef forward(self, x, y):#正向传播return x+ydef backward(self, dout):#反向传播return dout*1,dout*1激活函数层实现
在书的上一章实现了神经网络的学习,但是只有学习过程是不够的,还需要激活函数,对得到的结果进行取舍,书上在本章进行了激活函数层的实现。
ReLU
ReLU函数的性质不再赘述,可以参考神经网络简介,这里只给出计算图:

这里给出书上的实现,加上了一些注释:
class Relu:def __init__(self):self.mask = Nonedef forward(self, x):self.mask = (x <= 0)#返回所有非正下标out = x.copy()#深复制out[self.mask] = 0#对应下标全部置0return outdef backward(self, dout):dout[self.mask] = 0#对应下标全部置0return dout
Sigmoid
这里跳过了sigmod内部各个节点的传递过程,将其视为一个整体,直接给出计算图:

书上的实现:
class Sigmoid:def __init__(self):self.out = Nonedef forward(self, x):out = sigmoid(x)#输出self.out = out#赋值return outdef backward(self, dout):return dout*(1.0-self.out)*self.out#反向传播的导数式子
Affine/Softmax层实现
上文所给的函数,操作对象都是单个的数值,然而在神经网络中,我们操作的总是矩阵,因此需要对应的运算层来实现运算。
Affine
Affine用来实现神经网络的正向传播中的矩阵乘积运算,式子表达为 Y = X W + B Y=XW+B Y=XW+B,这里的计算图采用书上的例子,即取各数据维度: X X X为 ( 2 , ) (2,) (2,)、 W W W为 ( 2 , 3 ) (2,3) (2,3)、 B B B为 ( 3 , ) (3,) (3,),基本计算图如下:

基础版
矩阵计算图的反向传播和前文的道理一样,书上给出了反向传播的推导结果:
( 1 ) ∂ L ∂ X = ∂ L ∂ Y W T ( 2 ) ∂ L ∂ W = X T ∂ L ∂ Y \begin{aligned} (1)\frac{∂L}{∂X}=\frac{∂L}{∂Y}W^{T} \\ \\ (2)\frac{∂L}{∂W}=X^{T}\frac{∂L}{∂Y} \end{aligned} (1)∂X∂L=∂Y∂LWT(2)∂W∂L=XT∂Y∂L
反向传播的计算图如下,数字为对应的式子, X X X应该和 ∂ L ∂ X \frac{∂L}{∂X} ∂X∂L形状相同, W W W应该和 ∂ L ∂ W \frac{∂L}{∂W} ∂W∂L形状相同。

批版本
现在考虑N个数据一起进行正向传播的情况,即批版本Affine层,相较于只处理单个数据,批版本多加了一维,式子如下:
( 3 ) ∂ L ∂ B = ∂ L ∂ Y \begin{aligned} (3)\frac{∂L}{∂B}=\frac{∂L}{∂Y} \end{aligned} (3)∂B∂L=∂Y∂L
计算图如下,可以看到都多加了一维,输入从一个数组变成了矩阵。

需要注意的是,就偏置值来说,正向传播和反向传播的处理方式是不一样的,正向传播只需要对每个数据加上相同的偏置值,但是反向传播,由于上有传回的数据不同,所以得到的偏导也可能不同,所以反向传播时得到的应该是一个数组。
书上给出的实现如下:
class Affine:def __init__(self, W, b):self.W =Wself.b = bself.x = Noneself.original_x_shape = None# 权重和偏置参数的导数self.dW = Noneself.db = Nonedef forward(self, x):# 对应张量self.original_x_shape = x.shapex = x.reshape(x.shape[0], -1)#重新拉伸self.x = xreturn np.dot(self.x, self.W) + self.bdef backward(self, dout):dx = np.dot(dout, self.W.T)self.dW = np.dot(self.x.T, dout)self.db = np.sum(dout, axis=0) return dx.reshape(*self.original_x_shape)# 还原输入数据的形状(对应张量)
Softmax-with-Loss
书上给出的softmax层的实现包括了损失函数,因此叫Softmax-with-Loss,由于太过复杂没办法重绘,这里给出书上设计图:

简化版的如下,这里假设要进行三类分类。
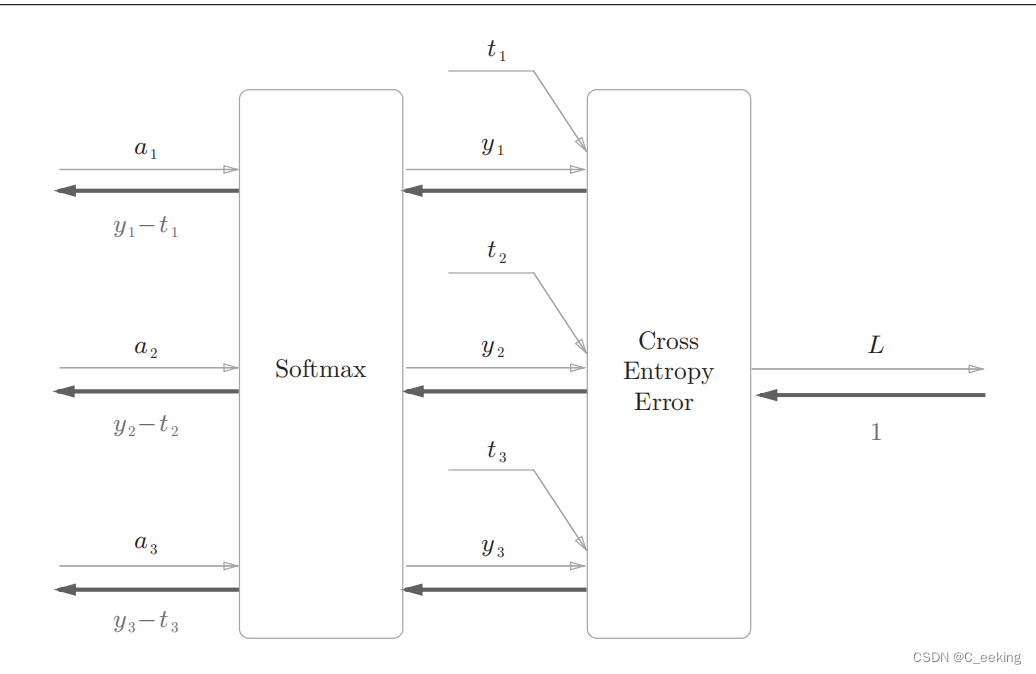 书上给出的代码实现如下:
书上给出的代码实现如下:
class SoftmaxWithLoss:def __init__(self):self.loss = Noneself.y = None # softmax的输出self.t = None # 监督数据def forward(self, x, t):self.t = tself.y = softmax(x)self.loss = cross_entropy_error(self.y, self.t)return self.lossdef backward(self, dout=1):#反向传播时要除以批大小,传递前面的层是单个数据的误差batch_size = self.t.shape[0]if self.t.size == self.y.size: # 监督数据是one-hot-vector的情况dx = (self.y - self.t) / batch_sizeelse:dx = self.y.copy()dx[np.arange(batch_size), self.t] -= 1dx = dx / batch_sizereturn dx
误差反向传播实现
上一章的神经网络实现使用数值微分求得,在使用时效率很低,如果使用误差反向传播效率会更高,这里给出书上的两层网络实现,加上了一些注释:
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import numpy as np
from common.layers import *
from common.gradient import numerical_gradient
from collections import OrderedDictclass TwoLayerNet:def __init__(self, input_size, hidden_size, output_size, weight_init_std = 0.01):#输入规模,隐藏层规模,输出规模,分布参数# 初始化权重self.params = {}self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)#高斯本部self.params['b1'] = np.zeros(hidden_size)#全置0self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size) self.params['b2'] = np.zeros(output_size)# 生成层self.layers = OrderedDict()#有序字典,记住向字典添加的顺序,可以认为拿字符串作为每一层的下标了self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])#传入参数,生成层self.layers['Relu1'] = Relu()self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])self.lastLayer = SoftmaxWithLoss()#最后一层def predict(self, x):#递推,每一层的结果作为下一层输入for layer in self.layers.values():x = layer.forward(x)return x# x:输入数据, t:监督数据def loss(self, x, t):y = self.predict(x)return self.lastLayer.forward(y, t)def accuracy(self, x, t):y = self.predict(x)y = np.argmax(y, axis=1)if t.ndim != 1 : t = np.argmax(t, axis=1)accuracy = np.sum(y == t) / float(x.shape[0])return accuracy# x:输入数据, t:监督数据def numerical_gradient(self, x, t):#反向传播算梯度loss_W = lambda W: self.loss(x, t)grads = {}grads['W1'] = numerical_gradient(loss_W, self.params['W1'])grads['b1'] = numerical_gradient(loss_W, self.params['b1'])grads['W2'] = numerical_gradient(loss_W, self.params['W2'])grads['b2'] = numerical_gradient(loss_W, self.params['b2'])return gradsdef gradient(self, x, t):# forwardself.loss(x, t)# backwarddout = 1dout = self.lastLayer.backward(dout)layers = list(self.layers.values())layers.reverse()for layer in layers:#一层层往回推dout = layer.backward(dout)# 设定grads = {}grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].dbgrads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].dbreturn grads
训练的源码略,只需要进行下列修改即可。
 学习的结果如下,输出的是训练集和测试集上的准确度:
学习的结果如下,输出的是训练集和测试集上的准确度:

梯度确认
与反向传播相比,数值微分的效率显得捉襟见肘,这是否意味着数值微分没有用武之地了呢?并不是,由于误差反向传播实现很复杂,所以很容易出错,因此,在用误差传播得到结果后,可以用数值微分的结果进行比对,确认误差传播的实现是否正确,这样的过程就是梯度确认,书上给的代码如下:
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)#拿数据network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)#构造神经网络x_batch = x_train[:3]
t_batch = t_train[:3]grad_numerical = network.numerical_gradient(x_batch, t_batch)#数值微分
grad_backprop = network.gradient(x_batch, t_batch)#反向传播for key in grad_numerical.keys():diff = np.average( np.abs(grad_backprop[key] - grad_numerical[key]) )#秋各个权重的绝对误差平均值print(key + ":" + str(diff))
运行结果:

总结
相较于数值微分,误差反向传播是一个更好的实现方式,但是理解上和实现上也增加了困难,并且由于其自身的复杂性,往往还需要数值微分进行结果的比对。
参考文献
- 《深度学习入门——基于Python的理论与实现》
相关文章:

误差反向传播简介与实现
误差反向传播 导语计算图反向传播链式法则 反向传播结构加法节点乘法节点 实现简单层加法乘法 激活函数层实现ReLUSigmoid Affine/Softmax层实现Affine基础版批版本 Softmax-with-Loss 误差反向传播实现梯度确认总结参考文献 导语 书上在前一章介绍了随机梯度下降法进行参数与…...
ATmega328P加硬件看门狗MAX824L看门狗
void Reversewdt(){ //硬件喂狗,11PIN接MAX824L芯片WDIif (digitalRead(11) HIGH) {digitalWrite(11, LOW); //低电平} else {digitalWrite(11, HIGH); //高电平 }loop增加喂狗调用 void loop() { …… Reversewdt();//喂狗 }...

【Redis】 String类型的内部编码与使用环境
文章目录 🍃前言🌴内部编码🎄典型使用场景🚩缓存功能🚩计数(Counter)功能🚩共享会话(Session)🚩验证码功能 ⭕总结 🍃前言 本篇文章重…...

HarmonyOS interface router scale pageTransition SlideEffect.Left ArkTS ArkUI
🎬️create Component export default struct TitleBar {build(){Row(){Text(transition).fontSize(30fp).fontColor(Color.White)}.width(100%).height(8%).backgroundColor(#4169E1).padding({left:10})}}🎞️interface export interface IList{ti…...
Go语言(Golang)的开发框架
在Go语言(Golang)的开发中,有多种开发框架可供选择,它们各自具有不同的特点和优势。以下是一些流行的Go语言开发框架,选择Go语言的开发框架时,需要考虑项目需求、团队熟悉度、社区支持、框架性能和可维护性…...
)
Python入门第三课——Python 数据类型(详细)
文章回顾 Python入门第一课——Python起步安装、Sublime Text安装教程,环境配置Python入门第二课——Python的变量和简单数据类型 目录 文章回顾前言一、Python的详细数据类型二、各种数据类型和使用方法1.Number(数字)2、String(…...

html入门
<!DOCTYPE html><!--每个文件都要加上这个,是html文件的主题--> <html><!--查不多就是c预言的main函数,从头括到尾部--><head><meta http-equiv"Content-Type" content"text/html;charsetutf-8" /…...

蓝桥杯杨辉三角
PREV-282 杨辉三角形【第十二届】【蓝桥杯省赛】【B组】 (二分查找 递推): 解析: 1.杨辉三角具有对称性: 2.杨辉三角具有一定规律 通过观察发现,第一次出现的地方一定在左部靠右的位置,所以从…...

【活动】开源与闭源大模型:探索未来趋势的双轨道路
🌈个人主页: 鑫宝Code 🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础 💫个人格言: "如无必要,勿增实体" 文章目录 开源与闭源大模型:探索未来趋势的双轨道路引言一、开源大模型&#…...
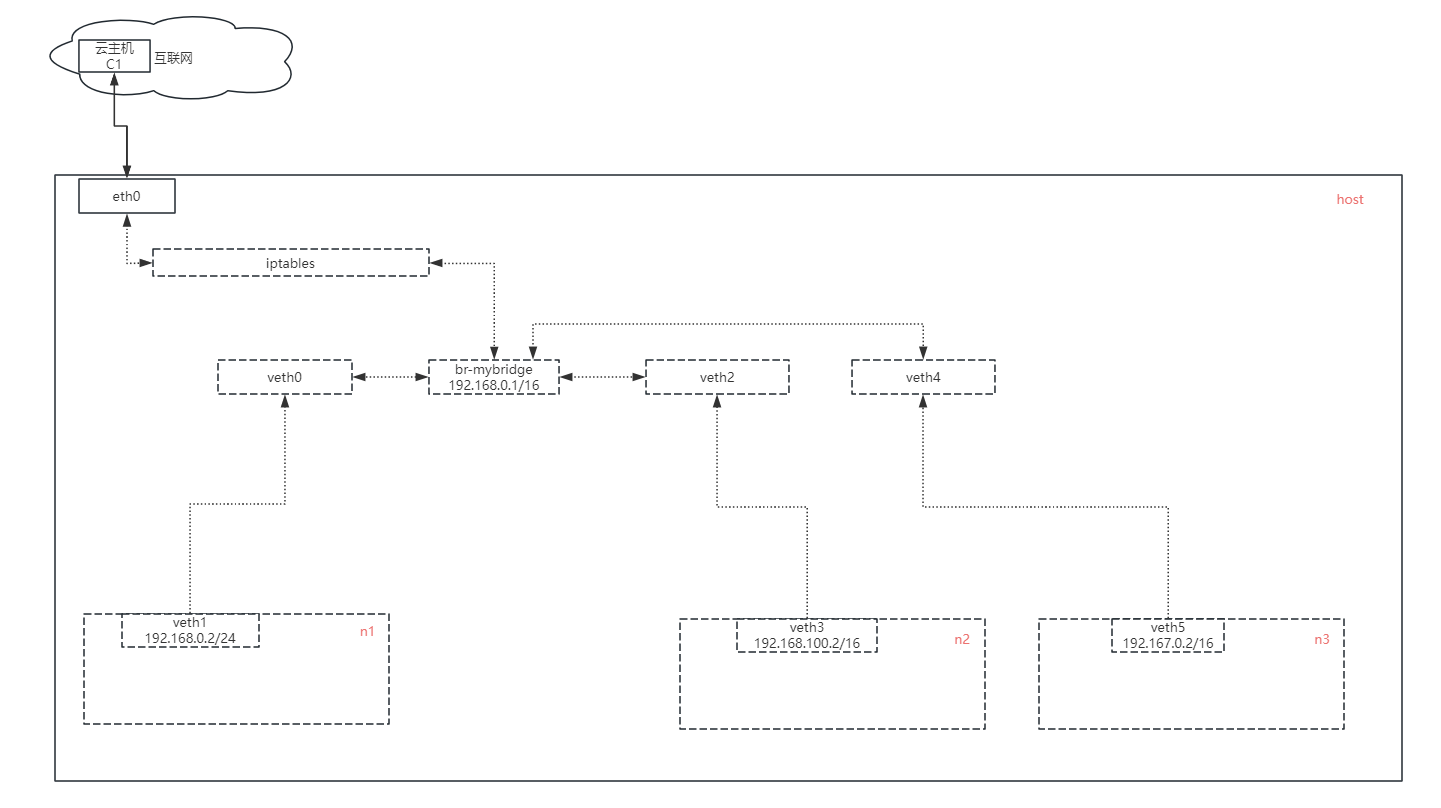
虚拟局域网(VLAN)
关键词:veth、vlan、bridge、iptables、nat、tcpdump、icmp、cidr、arp、路由表、计算机网络协议栈 前言 在过去的几十年里,互联网发展得非常快。许多新兴技术迅速崛起,也有不少曾经的主流技术被淘汰。然而,有些技术因为其基础性…...

内网穿透--Frp-简易型(速成)-上线
免责声明:本文仅做技术交流与学习... 目录 frp项目介绍: 一图通解: 编辑 1-下载frp 2-服务端(server)开启frp口 3-kali客户端(client)连接frp服务器 4-kali生成马子 5-kali监听 6-马子执行-->成功上线 frp项目介绍: GitHub - fatedier/frp: A fast reverse proxy…...

Python库之Scrapy的简介、安装、使用方法详细攻略
Python库之Scrapy的简介、安装、使用方法详细攻略 简介 Scrapy是一个快速的、高层次的web抓取和web抓取框架,用于抓取网站数据并从页面中提取结构化的数据。Scrapy用途广泛,可以用于数据挖掘、信息处理或存储历史数据,以及各种其他用途。 …...

k8s配置pods滚动发布
背景 采用微服务架构部署的应用,部署方式都要用到容器化部署k8s容器编排,最近我在公司负载的系统也是用的上述架构部署,但是随着系统的运行,用户提的需求就会越多,每次更新的话都要停机发布,最用户侧来说就…...
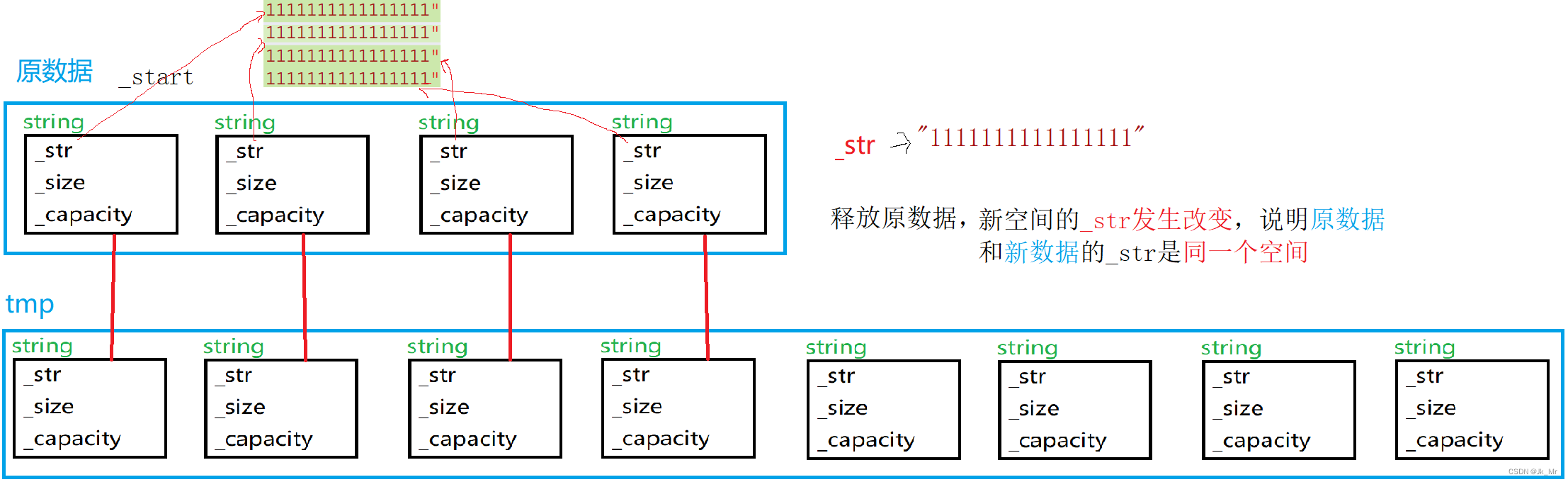
C++vector的简单模拟实现
文章目录 目录 文章目录 前言 一、vector使用时的注意事项 1.typedef的类型 2.vector不是string 3.vector 4.算法sort 二、vector的实现 1.通过源码进行猜测vector的结构 2.初步vector的构建 2.1 成员变量 2.2成员函数 2.2.1尾插和扩容 2.2.2operator[] 2.2.3 迭代器 2…...
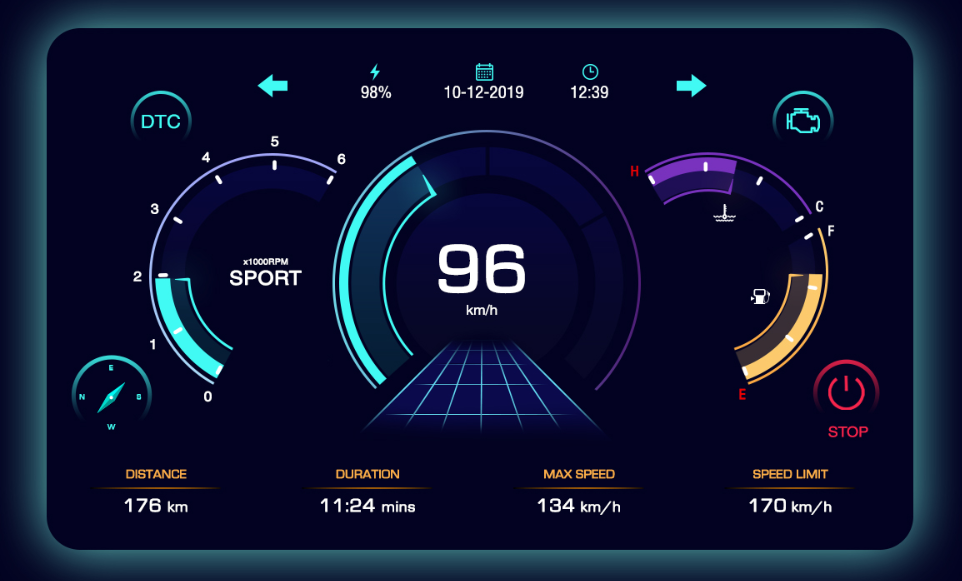
AWTK实现汽车仪表Cluster/DashBoard嵌入式GUI开发(七):快启
前言: 汽车仪表是人们了解汽车状况的窗口,而仪表中的大部分信息都是以指示灯形式显示给驾驶者。仪表指示灯图案都较为抽象,对驾驶不熟悉的人在理解仪表指示灯含义方面存在不同程度的困难,尤其对于驾驶新手,如果对指示灯的含义不求甚解,有可能影响驾驶的安全性。即使是对…...
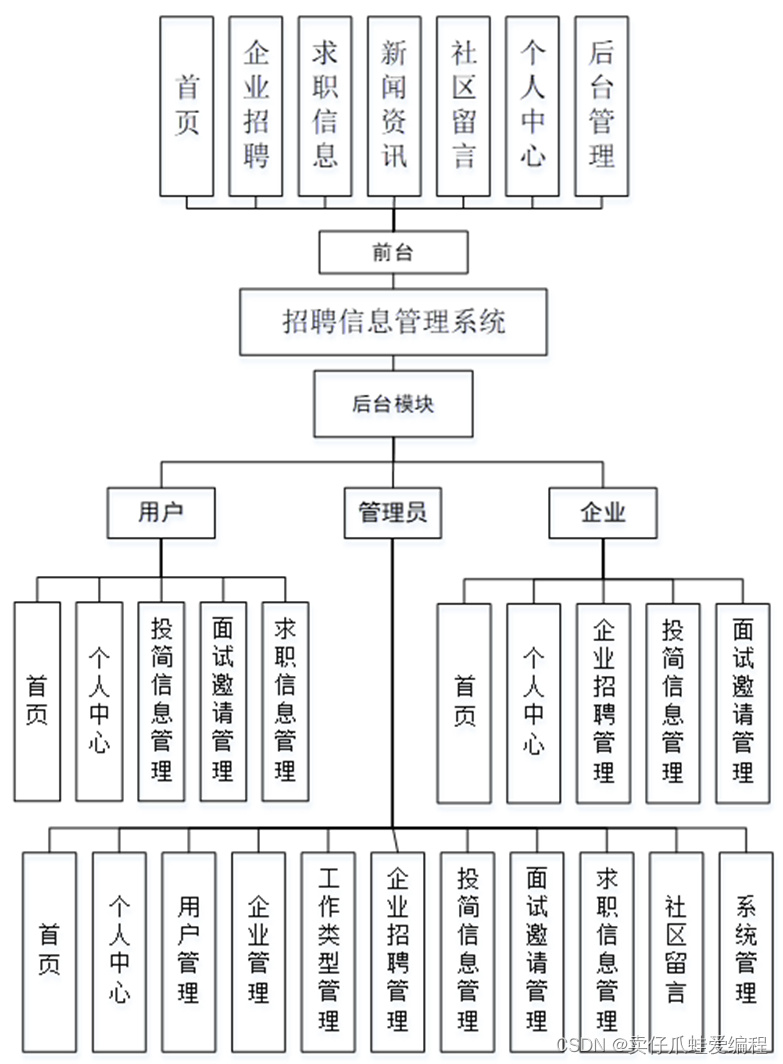
基于springboot+vue的招聘信息管理系统
开发语言:Java框架:springbootJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7(一定要5.7版本)数据库工具:Navicat11开发软件:eclipse/myeclipse/ideaMaven包:…...

使用STM32F103标准库实现自定义键盘
使用STM32F103标准库实现自定义键盘 在嵌入式系统中,自定义键盘的实现是一个经典的项目,能够帮助我们深入理解GPIO配置、按键扫描和中断处理等知识。本文将详细介绍如何使用STM32F103标准库来实现一个简单的自定义键盘。 1. 准备工作 1.1 硬件准备 S…...
面试八股之JVM篇3.5——垃圾回收——G1垃圾回收器
🌈hello,你好鸭,我是Ethan,一名不断学习的码农,很高兴你能来阅读。 ✔️目前博客主要更新Java系列、项目案例、计算机必学四件套等。 🏃人生之义,在于追求,不在成败,勤通…...
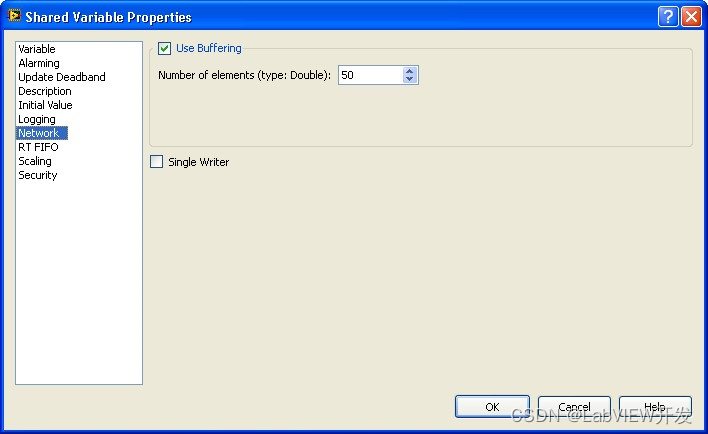
解决LabVIEW通过OPC Server读取PLC地址时的错误180121602
在使用LabVIEW通过OPC Server读取PLC地址时,若遇到错误代码180121602,建议检查网络连接、OPC Server和PLC配置、用户权限及LabVIEW设置。确保网络畅通,正确配置OPC变量,取消缓冲设置以实时读取数据,并使用诊断工具验证…...

npm,yarn,cnpm,tyarn,pnpm 安使用装配置镜像
npm 安装 安装node后就可以使用了 官方默认地址 npm config set registry https://registry.npmjs.org 镜像 npm config set registry https://registry.npm.taobao.org npm config set registry http://registry.npmmirror.org全局安装依赖 npm install -g <包名&g…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...
