1301-习题1-1高等数学
1. 求下列函数的自然定义域
自然定义域就是使函数有意义的定义域。
常见自然定义域:
- 开根号 x \sqrt x x: x ≥ 0 x \ge 0 x≥0
- 自变量为分式的分母 1 x \frac{1}{x} x1: x ≠ 0 x \ne 0 x=0
- 三角函数 tan x cot x \tan x \cot x tanxcotx: x ≠ π 2 + k π x\ne \frac{\pi}{2}+k\pi x=2π+kπ
- 反三角函数 arcsin x , arccos x \arcsin x,\arccos x arcsinx,arccosx: − 1 ≤ x ≤ 1 -1\le x\le 1 −1≤x≤1
- 反三角函数 arctan x \arctan x arctanx: x ∈ R x\in R x∈R
- 对数函数 ln x \ln x lnx: x > 0 x\gt 0 x>0
(3) y = 1 x − 1 − x 2 y=\frac{1}{x}-\sqrt{1-x^2} y=x1−1−x2
解: { x ≠ 0 , 1 − x 2 ≥ 0 得 − 1 ≤ x ≤ 1 且 x ≠ 0 ∴ D = [ − 1 , 0 ) ∪ ( 0 , 1 ] 解:\\ \begin{cases} x\ne 0,\\ 1-x^2\ge 0\\ \end{cases}\\ 得 -1\le x\le 1且x\ne 0\\ \therefore D=[-1,0)\cup(0,1] 解:{x=0,1−x2≥0得−1≤x≤1且x=0∴D=[−1,0)∪(0,1]
(8) y = 3 − x + arctan 1 x y=\sqrt{3-x}+\arctan{\frac{1}{x}} y=3−x+arctanx1
解: 该函数由 y 1 = 3 − x 与 y 2 = arctan 1 x 复合而成,所以应同时满足 { 3 − x ≥ 0 , x ≠ 0 得 x ≤ 3 且 x ≠ 0 ∴ 定义域 D = ( − ∞ , 0 ) ∪ ( 0 , 3 ] 解:\\ 该函数由y_1=\sqrt{3-x}与y_2=\arctan{\frac{1}{x}}复合而成,所以应同时满足\\ \begin{cases} 3-x\ge 0,\\ x\ne 0\\ \end{cases}\\ 得 x\le 3且x\ne 0\\ \therefore 定义域D = (-\infty, 0)\cup (0,3] 解:该函数由y1=3−x与y2=arctanx1复合而成,所以应同时满足{3−x≥0,x=0得x≤3且x=0∴定义域D=(−∞,0)∪(0,3]
2. 下列各题中,函数 f ( x ) 和 g ( x ) f(x)和g(x) f(x)和g(x)是否相同?为什么?
函数相同满足条件:定义域相同;函数关系相同;
Tips: 变量符号可不同
(3) f ( x ) = x 4 − x 3 3 , g ( x ) = x x − 1 3 f(x)=\sqrt[3]{x^4-x^3},g(x)=x\sqrt[3]{x-1} f(x)=3x4−x3,g(x)=x3x−1
f ( x ) 与 g ( x ) 相同 f ( x ) = x 4 − x 3 3 , x ∈ R 化简得 : f ( x ) = x x − 1 3 g ( x ) = x x − 1 3 , x ∈ R 定义域相同,函数关系相同,所以 f ( x ) 与 g ( x ) 相同 f(x)与g(x)相同\\ f(x)=\sqrt[3]{x^4-x^3},x\in R\\ 化简得:f(x)=x\sqrt[3]{x-1}\\ g(x)=x\sqrt[3]{x-1},x\in R\\ 定义域相同,函数关系相同,所以f(x)与g(x)相同 f(x)与g(x)相同f(x)=3x4−x3,x∈R化简得:f(x)=x3x−1g(x)=x3x−1,x∈R定义域相同,函数关系相同,所以f(x)与g(x)相同
(4) f ( x ) = 1 , g ( x ) = sec 2 x − tan 2 x f(x)=1,g(x)=\sec^2x-\tan^2x f(x)=1,g(x)=sec2x−tan2x
解: f ( x ) 定义域为 : D f = R g ( x ) 的定义域为 D g = ( − π 2 + k π , π 2 + k π ) , k ∈ Z ∴ f ( x ) 与 g ( x ) 不同 解:\\ f(x)定义域为:D_f=R\\ g(x)的定义域为D_g=(-\frac{\pi}{2}+k\pi,\frac{\pi}{2}+k\pi),k\in Z\\ \therefore f(x)与g(x)不同 解:f(x)定义域为:Df=Rg(x)的定义域为Dg=(−2π+kπ,2π+kπ),k∈Z∴f(x)与g(x)不同
3. 分段三角函数值和图形
ϕ ( x ) = { ∣ sin x ∣ , ∣ x ∣ < π 3 , 0 , ∣ x ∣ ≥ π 3 \phi(x)=\begin{cases} |\sin x|,\quad|x|\lt \frac{\pi}{3},\\ 0,\qquad\quad |x|\ge \frac{\pi}{3} \end{cases} ϕ(x)={∣sinx∣,∣x∣<3π,0,∣x∣≥3π
求 ϕ ( π 6 ) , ϕ ( π 4 ) , ϕ ( − π 4 ) , ϕ ( − 2 ) \phi(\frac{\pi}{6}),\phi(\frac{\pi}{4}),\phi(-\frac{\pi}{4}),\phi(-2) ϕ(6π),ϕ(4π),ϕ(−4π),ϕ(−2),并做出函数 y = ϕ ( x ) y=\phi(x) y=ϕ(x)的图形
解: ϕ ( π 6 ) = ∣ sin π 6 ∣ = 1 2 ϕ ( π 4 ) = 2 2 ϕ ( − π 4 ) = 2 2 ϕ ( − 2 ) = 0 解:\\ \phi(\frac{\pi}{6})=|\sin \frac{\pi}{6}|=\frac{1}{2}\\ \phi(\frac{\pi}{4})=\frac{\sqrt2}{2}\\ \phi(-\frac{\pi}{4})=\frac{\sqrt2}{2}\\ \phi(-2)=0 解:ϕ(6π)=∣sin6π∣=21ϕ(4π)=22ϕ(−4π)=22ϕ(−2)=0
图形如下图所示:

4. 试证下列函数在指定区间内的单调性:
(1) y = x 1 − x , ( − ∞ , 1 ) y=\frac{x}{1-x},(-\infty,1) y=1−xx,(−∞,1) (2) y = x + ln x , ( 0 , + ∞ ) y=x+\ln x,(0,+\infty) y=x+lnx,(0,+∞)
证明: ( 1 ) 设置 x 1 , x 2 ∈ ( − ∞ , 1 ) , 且 x 1 < x 2 f ( x 1 ) − f ( x 2 ) = x 1 1 − x 1 − x 2 1 − x 2 = x 1 − x 2 ( 1 − x 1 ) ( 1 − x 2 ) < 0 ∴ y = x 1 − x 在区间 ( − ∞ , 1 ) 上单调递增 ( 2 )设置 x 1 , x 2 ∈ ( 0 , + ∞ ) , 且 x 1 < x 2 f ( x 1 ) − f ( x 2 ) = x 1 + ln x 1 − ( x 2 + ln x 2 ) = ( x 1 − x 2 ) + ln x 1 x 2 < 0 ∴ y = x + ln x 在区间 ( 0 , + ∞ ) 区间上单调递增 证明:\\ (1)设置x_1,x_2\in (-\infty,1),且x_1\lt x_2\\ f(x_1)-f(x_2)=\frac{x_1}{1-x_1}-\frac{x_2}{1-x_2}\\ =\frac{x_1-x_2}{(1-x_1)(1-x_2)}\lt 0\\ \therefore y=\frac{x}{1-x}在区间(-\infty,1)上单调递增\\ (2)设置x_1,x_2\in (0,+\infty),且x_1\lt x_2\\ f(x_1)-f(x_2)=x_1+\ln x_1-(x_2+\ln x_2)\\ =(x_1-x_2)+\ln\frac{x_1}{x_2}\lt 0\\ \therefore y=x+\ln x在区间(0,+\infty)区间上单调递增 证明:(1)设置x1,x2∈(−∞,1),且x1<x2f(x1)−f(x2)=1−x1x1−1−x2x2=(1−x1)(1−x2)x1−x2<0∴y=1−xx在区间(−∞,1)上单调递增(2)设置x1,x2∈(0,+∞),且x1<x2f(x1)−f(x2)=x1+lnx1−(x2+lnx2)=(x1−x2)+lnx2x1<0∴y=x+lnx在区间(0,+∞)区间上单调递增
5. 奇偶性与单调性
设f(x)为定义在 ( − l , l ) (-l,l) (−l,l)内的奇函数,若f(x)在 ( 0 , l ) (0,l) (0,l)内单调增加,证明f(x)在 ( − l , 0 ) (-l,0) (−l,0)内也单调递增
证明: 设 x 1 , x 2 ∈ ( 0 , l ) , 且 x 1 < x 2 则 − x 1 , − x 2 ∈ ( − l , 0 ) , 且 − x 1 > − x 2 ∵ f ( x ) 在 ( − l , l ) 内为奇函数,则 f ( x ) = − f ( − x ) f ( x ) 在 ( 0 , l ) 内单调增加 f ( x 1 ) < f ( x 2 ) 即 − f ( − x 1 ) < − f ( − x 2 ) = > f ( − x 1 ) > f ( − x 2 ) 即 f ( x ) 在 ( − 1 , 0 ) 内也单调增加 证明:\\ 设x_1,x_2\in(0,l),且x_1\lt x_2\\ 则 -x_1,-x_2\in(-l,0),且-x_1\gt -x_2\\ \because f(x)在(-l,l)内为奇函数,则\\ f(x)=-f(-x)\\ f(x)在(0,l)内单调增加\\ f(x_1)\lt f(x_2)\\ 即-f(-x_1)\lt -f(-x_2)=>f(-x_1)\gt f(-x_2)\\ 即f(x)在(-1,0)内也单调增加 证明:设x1,x2∈(0,l),且x1<x2则−x1,−x2∈(−l,0),且−x1>−x2∵f(x)在(−l,l)内为奇函数,则f(x)=−f(−x)f(x)在(0,l)内单调增加f(x1)<f(x2)即−f(−x1)<−f(−x2)=>f(−x1)>f(−x2)即f(x)在(−1,0)内也单调增加
6. 奇偶运算结果的奇偶性
只给结论,不再证明
- 两个偶函数的和是偶函数,两个奇函数的和是奇函数。
- 两个偶函数的乘积是偶函数,两个奇函数的乘积是偶函数,偶函数与奇函数的乘积是奇函数。
8.周期函数的周期
(3) 1 + sin ( π x ) 1+\sin(\pi x) 1+sin(πx) 周期 2 (5) sin 2 x \sin^2x sin2x
sin 2 x = 1 − cos 2 x 2 周期为 π \sin^2x = \frac{1-\cos2x}{2}\\ 周期为\pi sin2x=21−cos2x周期为π
9.求下列函数的反函数
(2) y = 1 − x 1 + x y=\frac{1-x}{1+x} y=1+x1−x
解: y = 1 − x 1 + x y ( 1 + x ) = 1 − x y x + x = 1 − y x = 1 − y 1 + y , y ≠ − 1 f − 1 ( x ) = 1 − x 1 + x , x ≠ − 1 解:\\ y=\frac{1-x}{1+x}\\ y(1+x)=1-x\\ yx+x=1-y\\ x=\frac{1-y}{1+y},y\not=-1\\ f^{-1}(x)=\frac{1-x}{1+x},x\not=-1 解:y=1+x1−xy(1+x)=1−xyx+x=1−yx=1+y1−y,y=−1f−1(x)=1+x1−x,x=−1
(3) y = a x + b c x + d ( a d − b c ≠ 0 ) y=\frac{ax+b}{cx+d}(ad-bc\not=0) y=cx+dax+b(ad−bc=0)
解: y = a x + b c x + d y ( c x + d ) = a x + b c y x − a x = b − d y x = − d y + b c y − a 解:\\ y=\frac{ax+b}{cx+d}\\ y(cx+d)=ax+b\\ cyx-ax=b-dy\\ x=\frac{-dy+b}{cy-a} 解:y=cx+dax+by(cx+d)=ax+bcyx−ax=b−dyx=cy−a−dy+b
(6) y = 2 x 2 x + 1 y=\frac{2^x}{2^x+1} y=2x+12x
解: y = 2 x 2 x + 1 2 x ( 1 − y ) = y x = log 2 ( y 1 − y ) f − 1 ( x ) = log 2 ( y 1 − y ) 解:\\ y = \frac{2^x}{2^x+1}\\ 2^x(1-y)=y\\ x=\log_2(\frac{y}{1-y})\\ f^{-1}(x)=\log_2(\frac{y}{1-y}) 解:y=2x+12x2x(1−y)=yx=log2(1−yy)f−1(x)=log2(1−yy)
结语
❓QQ:806797785
⭐️文档笔记地址:https://gitee.com/gaogzhen/math
参考:
[1]同济大学数学系.高等数学 第七版 上册[M].北京:高等教育出版社,2014.7.p16-18.
[2]同济《高等数学》第七版-课后题逐题讲解[CP/OL].2023-07-26.p1.
相关文章:

1301-习题1-1高等数学
1. 求下列函数的自然定义域 自然定义域就是使函数有意义的定义域。 常见自然定义域: 开根号 x \sqrt x x : x ≥ 0 x \ge 0 x≥0自变量为分式的分母 1 x \frac{1}{x} x1: x ≠ 0 x \ne 0 x0三角函数 tan x cot x \tan x \cot x …...
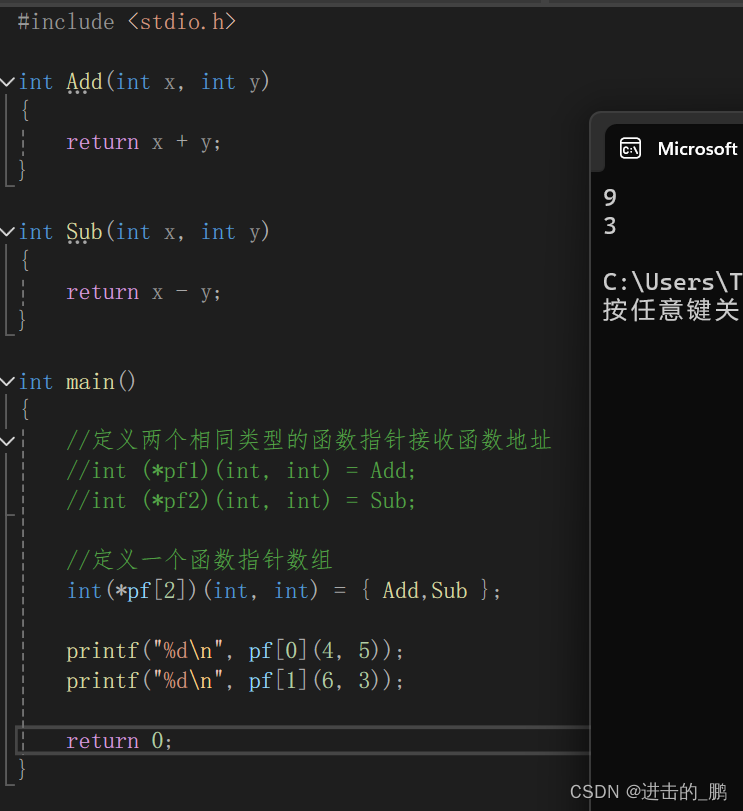
C语言之指针进阶(3),函数指针
目录 前言: 一、函数指针变量的概念 二、函数指针变量的创建 三、函数指针变量的使用 四、两段特殊代码的理解 五、typedef 六、函数指针数组 总结: 前言: 本文主要讲述C语言指针中的函数指针,包括函数指针变量的概念、创建…...
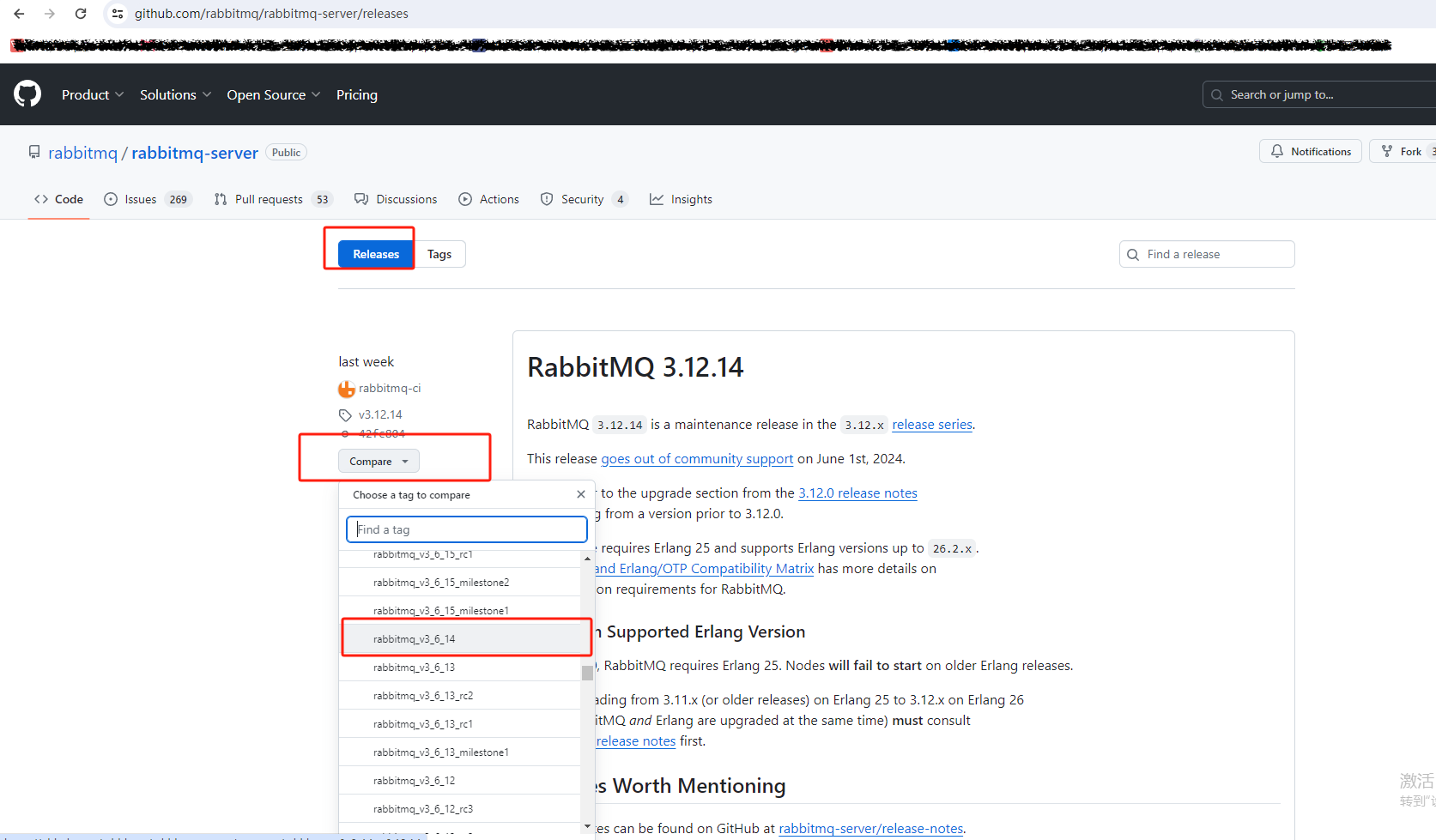
RabbitMQ安装及配套Laravel使用
MQ MQ 全称 Message Queue(消息队列),是在消息的传输过程中保存消息的容器。多用于系统之间的异步通信。 为什么需要mq: 解耦:MQ能够使各个系统或组件之间解耦,降低它们之间的耦合度,提高系统的灵活性和可维护性异步处理:通过MQ可以实现异步处理,提高系统响应速度和吞…...
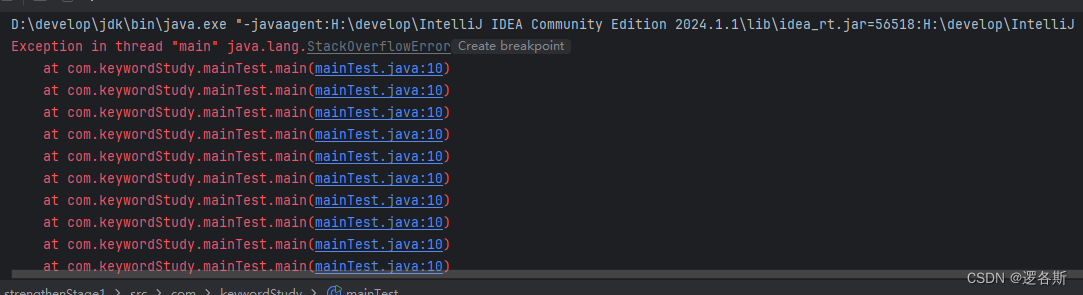
java在类的定义中创建自己的对象?
当在main方法中新建自身所在类的对象,并调用main方法时,会不断循环调用main方法,直到栈溢出 package com.keywordStudy;public class mainTest {static int value 33;public static void main(String[] args) throws Exception{String[] sn…...

掌握C++回调:按值捕获、按引用捕获与弱引用
文章目录 一、按引用捕获和按值捕获1.1 原理1.2 案例 二、弱引用2.1 原理2.2 案例一2.3 案例二:使用base库的弱引用 三、总结 在C回调中,当使用Lambda表达式捕获外部变量时,有两种捕获方式:按值捕获和按引用捕获。 一、按引用捕获…...

抖音运营_如何做出优质的短视频
目录 一 短视频内容的构成 1 图像 2 字幕 3 声音 4 特效 5 描述 6 评论 二 短视频的热门类型 1 颜值圈粉类 2 知识教学类 3 幽默搞笑类 4 商品展示类 5 才艺技能类 6 评论解说类 三 热门短视频的特征 1 产生共鸣 2 正能量 3 紧跟热点话题 4 富有创意 四 短视…...

Day21:Leetcode513.找树左下角的值 +112. 路径总和 113.路径总和ii + 106.从中序与后序遍历序列构造二叉树
LeetCode:513.找树左下角的值 解决方案: 1.思路 在遍历一个节点时,需要先把它的非空右子节点放入队列,然后再把它的非空左子节点放入队列,这样才能保证从右到左遍历每一层的节点。广度优先搜索所遍历的最后一个节点…...
)
Java数据结构和算法(B树)
前言 B树又叫平衡的多路搜索树;平衡的意思是又满足平衡二叉树的一些性质,左树大于右树; 多路意思是,可以多个结点,不再是像二叉树只有两个结点; 实现原理 B树是一种自平衡的搜索树,通常用于实…...

成为程序员后我都明白了什么?从入行到弃坑?
作为一个入行近10年的php程序员,真心感觉一切都才刚开始,对计算机,编程语言的理解也好,程序员中年危机也罢,之前都是听别人说的,真的自己到了这个水平,这个年龄才深刻体会到这其中的种种。 我一…...

python --创建固定字符串长度,先进先出
a 123def concatenate_within_limit(b, new_string):# 计算新字符串与a的长度之和a btotal_length len(a) len(new_string)# 如果长度超过1024,从前面删除足够的字符if total_length > 5:diff total_length - 5a a[diff:] new_string # 删除前diff个字符…...

容器化部署
目录 docker容器化部署 怎样使用Docker Compose或Kubernetes等容器编排工具来管理和扩展联邦学习系统 使用Docker Compose...

国产数据库TiDB的常用方法
TiDB的常用方法主要涉及安装配置、数据操作、性能调优以及监控和维护等方面。以下是对这些常用方法的归纳和介绍: 1. 安装与配置 安装TiDB:根据官方文档的指引,用户可以按照步骤进行TiDB的安装。配置TiDB:安装完成后,…...

基于DdddOcr通用验证码离线本地识别SDK搭建个人云打码接口Api
前言 最近介绍了一款免费的验证码识别网站,识别效率太低,考虑到ddddocr是开源的,决定搭建搭建一个,发现原作者sml2h3已经推出好久了,但是网上没有宝塔安装的教程,于是本次通过宝塔搭建属于自己的带带弟弟OCR通用验证码离线本地识别 原项目地址:https://github.com/sml2…...
2、xss-labs之level2
1、打开页面 2、传入xss代码 payload:<script>alert(xss)</script>,发现返回<script>alert(xss)</script> 3、分析原因 打开f12,没什么发现 看后端源码,在这form表单通过get获取keyword的值赋给$str&am…...
人才测评的应用:人才选拔,岗位晋升,面试招聘测评
人才测评自诞生以来,就被广泛应用在各大方面,不仅是我们熟悉的招聘上,还有其他考核和晋升,都会需要用到人才测评。不知道怎么招聘?或者不懂得如何实现人才晋升?都可以参考人才测评,利用它帮我们…...

前端面试题日常练-day33 【面试题】
题目 希望这些选择题能够帮助您进行前端面试的准备,答案在文末。 在jQuery中,以下哪个选项用于在元素上绑定一个点击事件? a) click() b) bind() c) on() d) trigger() jQuery中,以下哪个选项用于获取元素的属性值? …...

非整数倍数据位宽转换24to128
描述 实现数据位宽转换电路,实现24bit数据输入转换为128bit数据输出。其中,先到的数据应置于输出的高bit位。 电路的接口如下图所示。valid_in用来指示数据输入data_in的有效性,valid_out用来指示数据输出data_out的有效性;clk是时…...
html通过数据改变,图片跟着改变
改变前 改变后 通过数据来控制样式展示 <template><div>通过num控制图标是否更改{{num}}<div class"box"><!-- 如果num大于1则是另一种,样式,如果小时1,则是另一种样式 --><div class"item&qu…...
centos7.9 安装SqlServer
1、导入Microsoft SQL Server CentOS存储库: sudo curl -o /etc/yum.repos.d/mssql-server.repo https://packages.microsoft.com/config/rhel/7/mssql-server-2019.repo2、安装SQL Server: sudo yum install -y mssql-server假如机器内存不足2G 需要对…...

Idea中flume的Interceptor的编写教程
1.新建-项目-新建项目 注意位置是将来打包文件存放的位置,即我们打包好的文件在这/export/data个目录下寻找 2. 在maven项目中导入依赖 Pom.xml文件中写入 <dependencies> <dependency> <groupId>org.apache.flume</groupId> <artifa…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...
