29. 相似矩阵,若尔当型
文章目录
- 1. 相似矩阵
- 2. 相似矩阵
- 2.1 举例
- 2.2 证明相似矩阵具有相同特征值
1. 相似矩阵
假设矩阵A,B为正定矩阵,那么对于任意非零列向量x来说,二次型 x T A x , x T B x x^TAx,x^TBx xTAx,xTBx恒为正
x T A x > 0 , x T B x > 0 , \begin{equation} x^TAx>0,x^TBx>0, \end{equation} xTAx>0,xTBx>0,
- 如果A,B均是正定矩阵,那么A+B也是正定矩阵
x T ( A + B ) x = ( x T A + x T B ) x = x T A x + x T B x > 0 \begin{equation} x^T(A+B)x=(x^TA+x^TB)x=x^TAx+x^TBx>0 \end{equation} xT(A+B)x=(xTA+xTB)x=xTAx+xTBx>0
我们在做最小二乘法的过程中,需要拟合一条直线,满足直线基本能反映点的情况,我们知道b值不一定在A的列空间中,所以我们通过同时乘以 A T A^T AT 得到 A T b A^Tb ATb,使得方程能求得最优解 x ^ \hat{x} x^
A T A x ^ = A T b \begin{equation} A^TA\hat{x}=A^Tb \end{equation} ATAx^=ATb
这时候我们就遇到了 A T A A^TA ATA矩阵,那么这个矩阵肯定是对称矩阵,请问 A T A A^TA ATA 是否是正定矩阵呢?
1.1 A T A A^TA ATA正定性证明
首先 A T A A^TA ATA是对称的,那么我们只需要证明对于任意非零向量x,二次型恒正即可:
x T A T A x > ? ? ? 0 \begin{equation} x^TA^TAx>???0 \end{equation} xTATAx>???0
- 整理上述公式可得:
( x T A T ) ( A x ) = ( A x ) T ( A x ) \begin{equation} (x^TA^T)(Ax)=(Ax)^T(Ax) \end{equation} (xTAT)(Ax)=(Ax)T(Ax) - 我们知道Ax表示的是A列向量的组合,最后还是一个列向量,所以上述值都是一个标量的平方,所以可以得到如下:
( x T A T ) ( A x ) = ( A x ) T ( A x ) = ∣ ∣ A x ∣ ∣ 2 ≥ 0 \begin{equation} (x^TA^T)(Ax)=(Ax)^T(Ax)=||Ax||^2 \ge 0 \end{equation} (xTAT)(Ax)=(Ax)T(Ax)=∣∣Ax∣∣2≥0 - 那么什么时候 ∣ ∣ A x ∣ ∣ ≠ 0 ||Ax|| \neq0 ∣∣Ax∣∣=0呢?也就是当Ax=0无零解,也就是说矩阵A的秩等于列数n,所以可以得到,只要给定一个m行n列的矩阵A,如果矩阵A的秩为n,即满列秩,那么就可以得到 A T A A^TA ATA为正定矩阵!!!
2. 相似矩阵
假设A,B均是N×N的矩阵,如果存在一个可以矩阵M,使得三个矩阵满足如下关系,那么A相似于B
B = M − 1 A M \begin{equation} B=M^{-1}AM \end{equation} B=M−1AM
特征向量矩阵S,当我们有一个矩阵A,其特征值矩阵为 Λ \Lambda Λ,特征向量矩阵为S,满足如下条件:
Λ = S − 1 A S ⇒ A ∼ Λ \begin{equation} \Lambda=S^{-1}AS \Rightarrow A \sim \Lambda \end{equation} Λ=S−1AS⇒A∼Λ
- 按照新的说法来说,矩阵A相似于特征向量 Λ \Lambda Λ,也就是说当矩阵M是特征向量矩阵S时候,矩阵A相似于特征值矩阵 Λ \Lambda Λ,如果 M ≠ S M \ne S M=S,那么矩阵A相似于其他的。
B = M − 1 A M ⇒ { A ∼ Λ , M = S A ∼ B , M ≠ S \begin{equation} B=M^{-1}AM \Rightarrow \left\{ \begin{aligned} A \sim \Lambda,M=S\\ A \sim B,M\neq S\\ \end{aligned} \right.\end{equation} B=M−1AM⇒{A∼Λ,M=SA∼B,M=S
2.1 举例
当我们矩阵A表示如下,可以得到其特征向量矩阵S,特征值矩阵 Λ \Lambda Λ
A = [ 2 1 1 2 ] ⇒ S = [ 1 1 − 1 1 ] , Λ = [ 1 0 0 3 ] ⇒ A ∼ Λ \begin{equation} A=\begin{bmatrix} 2&1\\\\ 1&2 \end{bmatrix}\Rightarrow S=\begin{bmatrix} 1&1\\\\ -1&1 \end{bmatrix},\Lambda=\begin{bmatrix} 1&0\\\\ 0&3 \end{bmatrix}\Rightarrow A \sim \Lambda \end{equation} A= 2112 ⇒S= 1−111 ,Λ= 1003 ⇒A∼Λ
- 给定一个矩阵M,可得如下B
A = [ 2 1 1 2 ] ⇒ M = [ 1 4 0 1 ] , B = M − 1 A M = [ − 2 − 15 1 6 ] ⇒ A ∼ B \begin{equation} A=\begin{bmatrix} 2&1\\\\ 1&2 \end{bmatrix}\Rightarrow M=\begin{bmatrix} 1&4\\\\ 0&1 \end{bmatrix},B=M^{-1}AM=\begin{bmatrix} -2&-15\\\\ 1&6 \end{bmatrix}\Rightarrow A \sim B \end{equation} A= 2112 ⇒M= 1041 ,B=M−1AM= −21−156 ⇒A∼B - 矩阵A,B, Λ \Lambda Λ之间有什么关系呢?
∣ ∣ A ∣ ∣ = 3 , λ A 1 = 1 ; λ A 2 = 3 ; t r a c e A = 4 \begin{equation} ||A||=3,\lambda_{A1}=1;\lambda_{A2}=3;trace_A=4 \end{equation} ∣∣A∣∣=3,λA1=1;λA2=3;traceA=4
∣ ∣ B ∣ ∣ = 3 , λ B 1 = 1 ; λ B 2 = 3 ; t r a c e B = 4 \begin{equation} ||B||=3,\lambda_{B1}=1;\lambda_{B2}=3;trace_B=4 \end{equation} ∣∣B∣∣=3,λB1=1;λB2=3;traceB=4
1、两者的秩相等。 2、两者的行列式值相等。 3、两者的迹数相等。 4、两者拥有同样的特征值,尽管相应的特征向量一般不同
2.2 证明相似矩阵具有相同特征值
B = M − 1 A M , A x = λ x \begin{equation} B=M^{-1}AM,Ax=\lambda x \end{equation} B=M−1AM,Ax=λx
M B M − 1 = A ⇒ M B M − 1 x = A x = λ x ⇒ B [ M − 1 x ] = λ [ M − 1 x ] \begin{equation} MBM^{-1}=A\Rightarrow MBM^{-1}x=Ax=\lambda x \Rightarrow B[M^{-1}x]=\lambda [M^{-1}x] \end{equation} MBM−1=A⇒MBM−1x=Ax=λx⇒B[M−1x]=λ[M−1x]
- 故可以得到,如果矩阵A相似于矩阵B,那么A,B具有相同的特征值矩阵。
相关文章:

29. 相似矩阵,若尔当型
文章目录 1. 相似矩阵1.1 A T A A^TA ATA正定性证明 2. 相似矩阵2.1 举例2.2 证明相似矩阵具有相同特征值 1. 相似矩阵 假设矩阵A,B为正定矩阵,那么对于任意非零列向量x来说,二次型 x T A x , x T B x x^TAx,x^TBx xTAx,xTBx恒为正 x T A …...
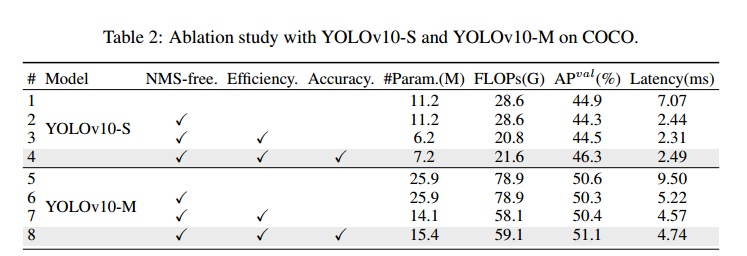
【论文阅读】 YOLOv10: Real-Time End-to-End Object Detection
文章目录 AbstractIntroductionRelated WorkMethodologyConsistent Dual Assignments for NMS-free Training (无NMS训练的一致性双重任务分配)Holistic Efficiency-Accuracy Driven Model Design (效率-精度驱动的整体模型设计) …...

Python读写文件
最近得以空闲,然后继续学习py。 学习一下py中最频繁用到的文件读写的方法。 在py中,操作是通过文件对象【File obj】实现的,通过文件对象可以读写文本文件和一些二进制文件。 1.打开文件 使用Python中的open函数。有8个参数,但…...
docker-如何将容器外的脚本放入容器内,将容器内的脚本放入容器外
文章目录 前言docker-如何将容器外的脚本放入容器内,将容器内的脚本放入容器外、1. docker 如何将容器外的脚本放入容器内1.1. 验证 2. 将容器内的脚本放入容器外 前言 如果您觉得有用的话,记得给博主点个赞,评论,收藏一键三连啊&…...

算法训练营第三十九天 | LeetCode 738 单调递增的数字、LeetCode 968 监控二叉树
LeetCode 738 单调递增的数字 这题类似模拟,可以找出如下规律: 先将数字按位数从高位到低位存到一个整型数组中。在这个数组中,从左往右遍历,如果遇到一个两数相等,并且记录的这个变量之前没有赋过值,那么…...

Hive语法学习总结
Hive SQL语法学习总结 hive参数库操作1.创建库2.具体案例3.库的其他操作 表和库的路径演示表的操作创建表插入数据 hive参数 一 hive常用交互命令hive -e sql语句hive -f sql文件 //文件中是sql语句二 参数的设置方式一:在客户端中设置参数(当次有效)set 参数名参…...

【Linux】TCP协议【中】{确认应答机制/超时重传机制/连接管理机制}
文章目录 1.确认应答机制2.超时重传机制:超时不一定是真超时了3.连接管理机制 1.确认应答机制 TCP协议中的确认应答机制是确保数据可靠传输的关键部分。以下是该机制的主要步骤和特点的详细解释: 数据分段与发送: 发送方将要发送的数据分成一…...

solidworks画螺母学习笔记
螺母 单位mm 六边形 直径16mm,水平约束,内圆直径10mm 拉伸 选择两侧对称,厚度7mm 拉伸切除 画相切圆 切除深度7mm,反向切除 拔模角度45 镜像切除 倒角 直径1mm 异形孔向导 螺纹线 偏移打勾,距离为2mm…...
WebGL的医学培训软件开发
开发基于WebGL的医学培训软件是一项复杂且技术性强的任务,需要结合医学专业知识和计算机图形学技术。以下是详细的开发流程和关键步骤。北京木奇移动技术有限公司,专业的软件外包开发公司,欢迎交流合作。 1.需求分析与定义 目标用户…...

新时代AI浪潮下,程序员和产品经理如何入局AIGC领域?
当下,AI浪潮席卷全球,AIGC大模型技术已经成为当今技术领域的一个重要趋势,对于产品经理来说,掌握这项技术不仅能够增强他们的职业技能,还能在竞争激烈的职场中脱颖而出。 为什么呢? 把握AI时代的机遇 AI技…...
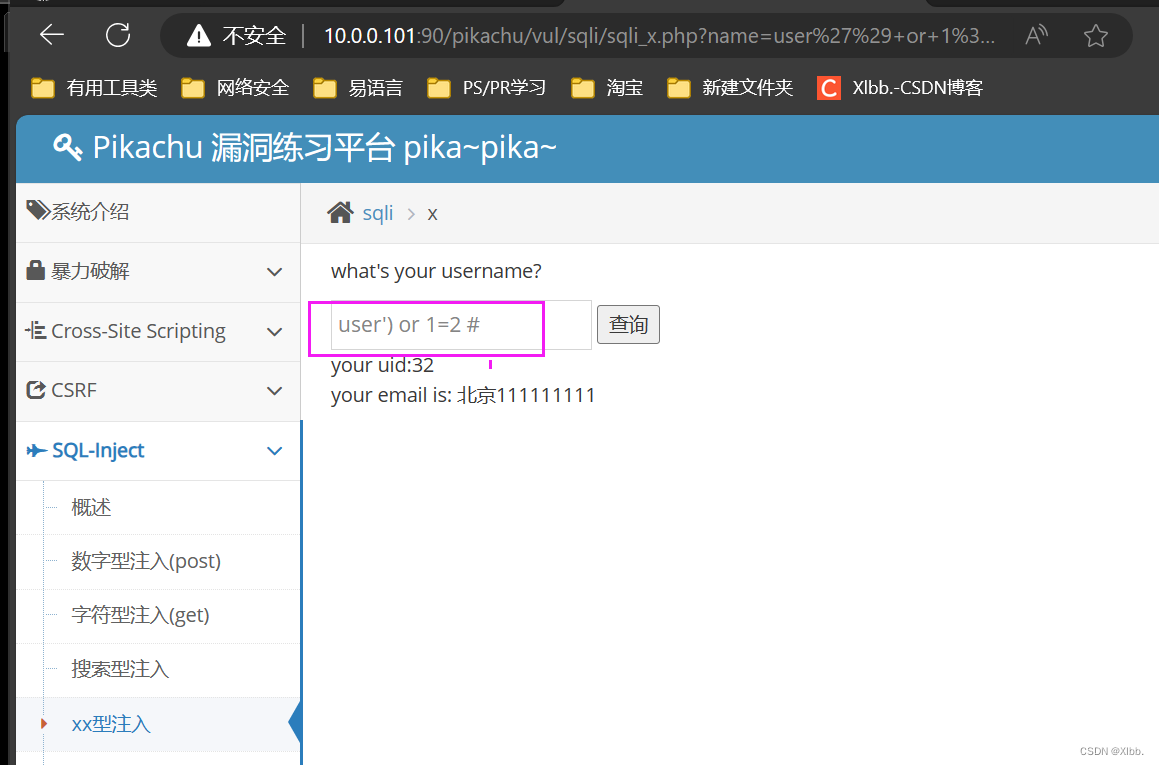
OWASP top10--SQL注入(一)
SQL注入式攻击技术,一般针对基于Web平台的应用程序.造成SQL注入攻击漏洞的原因,是由于程序员在编写Web程序时,没有对浏览器端提交的参数进行严格的过滤和判断。用户可以修改构造参数,提交SQL查询语句,并传递至服务器端…...

java —— 类与方法
一、访问修饰符 在类和方法中,均可使用访问修饰符以锁定该类或方法的被访问权限。访问修饰符有四种: (一)public 同一个项目中,对所有的类可见。 (二)protected 同一个项目中,对…...

【MySQL精通之路】InnoDB-启动选项和系统变量
系统变量可以在服务器启动时设置TRUE或FALSE启用禁用,也可以通过使用--skip前缀来禁用 例如: 要启用或禁用InnoDB自适应哈希索引,可以在命令行中使用--skip-innodb-adaptive-hash-index或--innodb-adaptive-hash-index,或者在配置…...

嵌入式linux系统中文件系统制作方法详解
第一:制作目的 1、掌握嵌入式Ubuntu系统的构建方法 2、熟悉嵌入式Ubuntu文件系统映射压缩打包方法 3、掌握RK3399linux系统单文件系统更新方法 Ubuntu根文件系统制作完成之后,把制作好的ubuntu文件系统映射文件在出厂系统的基础上替换原有的ubuntu根文件系统,即对 Linux 系统…...

AI爆文写作:要写文章爆,这47个爆文前缀少不了!
47个爆文前缀:很震惊很好用 这些前缀,虽然被用了无数次,但每个人看到还是会忍不住点进去。 可以借鉴这样强情绪的句式。 序号前缀1就在刚刚…2真相曝光…3震惊国人…4惊天秘密…5疯狂转发…6删前速看…7千万别吃…8还敢喝吗…9癌症前兆…10赶快扔了…11太可怕了…12大事不…...
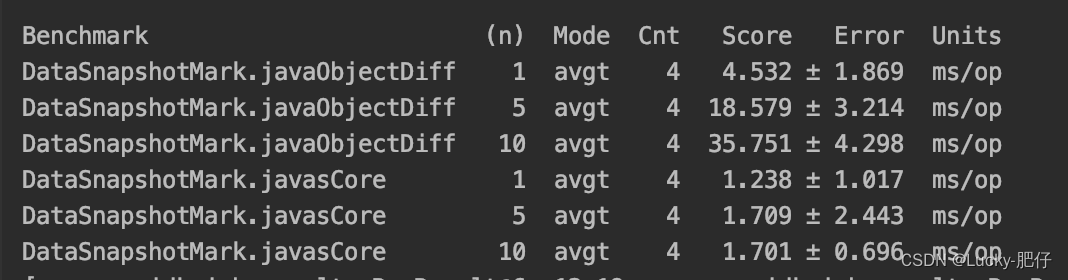
javas-core VS java-object-diff
对照工具选择 javas-core 和 java-object-diff ,对比demo https://github.com/kofgame/objectdiff-vs-javers,都为同源对比,都支持嵌套对象。 使用JMH测试方法进行性能测试,使用题库的QuestionResponseVO对象来进行对照对比,进行…...

dirsearch指令大全
文章目录 基本用法主要参数和选项目标和URL设置--url URL--url-list FILE 扩展名--extensions EXTENSIONS 字典文件--wordlists WORDLIST 线程和性能--threads THREADS--timeout SECONDS--delay MILLISECONDS 忽略状态码代理和请求设置--proxy PROXY--headers HEADERS 保存结果…...

C++基础:构建者设计模式
#include <iostream> #include <string> using namespace std; //构建者设计模式-一种工厂只生产一种复杂的产品 class robot {public:string head;string upbody;string downbody; };class robotBuilder {private:robot *myRobot;public:robotBuilder() //构造函…...

Swift 请求用户授权以跟踪其跨应用或网站的活动
步骤1:导入框架 首先,需要在Swift文件中导入AppTrackingTransparency框架。 import AppTrackingTransparency import AdSupport步骤2:请求跟踪许可 在适当的地方请求用户的跟踪许可。通常,这个请求会在应用启动时或者在用户执行…...

最新版npm详解
如:npm中搜索 jQuery image.png image.png 接地气的描述:npm 类似于如下各大手机应用市场 image.png image.png 查看本地 node 和 npm 是否安装成功 image.png image.png 或 npm install -g npm image.png image.png image.png image.png image.…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...

echarts使用graphic强行给图增加一个边框(边框根据自己的图形大小设置)- 适用于无法使用dom的样式
pdf-lib https://blog.csdn.net/Shi_haoliu/article/details/148157624?spm1001.2014.3001.5501 为了完成在pdf中导出echarts图,如果边框加在dom上面,pdf-lib导出svg的时候并不会导出边框,所以只能在echarts图上面加边框 grid的边框是在图里…...

写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里
写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里 脚本1 #!/bin/bash #定义变量 ip10.1.1 #循环去ping主机的IP for ((i1;i<10;i)) doping -c1 $ip.$i &>/dev/null[ $? -eq 0 ] &&am…...

用js实现常见排序算法
以下是几种常见排序算法的 JS实现,包括选择排序、冒泡排序、插入排序、快速排序和归并排序,以及每种算法的特点和复杂度分析 1. 选择排序(Selection Sort) 核心思想:每次从未排序部分选择最小元素,与未排…...

比较数据迁移后MySQL数据库和ClickHouse数据仓库中的表
设计一个MySQL数据库和Clickhouse数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

多模态大语言模型arxiv论文略读(110)
CoVLA: Comprehensive Vision-Language-Action Dataset for Autonomous Driving ➡️ 论文标题:CoVLA: Comprehensive Vision-Language-Action Dataset for Autonomous Driving ➡️ 论文作者:Hidehisa Arai, Keita Miwa, Kento Sasaki, Yu Yamaguchi, …...
